第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
Deep-Learning-Based Millimeter-Wave Massive MIMO for Hybrid Prec....pdf
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 68, NO. 3, MARCH 2019
3027
Deep-Learning-Based Millimeter-Wave Massive
MIMO for Hybrid Precoding
Hongji Huang
, Member, IEEE, Yiwei Song,
Jie Yang, Member, IEEE, Guan Gui
, Senior Member, IEEE,
and Fumiyuki Adachi
, Life Fellow, IEEE
Abstract—Millimeter wave (mmWave) massive multiple-input multiple-
output (MIMO) has been regarded to be an emerging solution for the next
generation of communications, in which hybrid analog and digital pre-
coding is an important method for reducing the hardware complexity and
energy consumption associated with mixed signal components. However,
the fundamental limitations of the existing hybrid precoding schemes are
that they have high-computational complexity and fail to fully exploit the
spatial information. To overcome these limitations, this paper proposes a
deep-learning-enabled mmWave massive MIMO framework for effective
hybrid precoding, in which each selection of the precoders for obtaining
the optimized decoder is regarded as a mapping relation in the deep neural
network (DNN). Specifically, the hybrid precoder is selected through train-
ing based on the DNN for optimizing precoding process of the mmWave
massive MIMO. Additionally, we present extensive simulation results to
validate the excellent performance of the proposed scheme. The results
exhibit that the DNN-based approach is capable of minimizing the bit er-
ror ratio and enhancing the spectrum efficiency of the mmWave massive
MIMO, which achieves better performance in hybrid precoding compared
with conventional schemes while substantially reducing the required com-
putational complexity.
Index Terms—Millimeter wave (mmWave), massive multiple-input
multiple-output (MIMO), deep learning, hybrid precoding.
I. INTRODUCTION
Wireless data traffic is predicted to improve 1000-fold by the year
2020 and may increase by over 10 000-fold by the year 2030 [1], thus
promoting the development of the fifth generation (5G) concept to cope
with the explosive data increase. As one of the most highly efficient
techniques to meet the 5G requirements, the use of enormous chunks
of under-utilized spectrum in the ultra-high-frequency bands, such as
the millimeter-wave (mmWave) band, has recently attracted consid-
erable interest in the research community [2]. Compare with current
wireless systems, one evolutionary progress of mmWave communi-
cations is that the ten-fold increase in carrier frequency. In another
words, mmWave signals bring an orders-of-magnitude enhancement in
free-space pathloss [3].
Inspired by massive multiple-input multiple-output (MIMO), a
mmWave massive MIMO system is considered to be a potential tech-
Manuscript received November 18, 2018; accepted January 15, 2019. Date
of publication January 18, 2019; date of current version March 14, 2019. This
work was supported by the Priority Academic Program Development of Jiangsu
Higher Education Institutions. The review of this paper was coordinated by
Dr. A.-C. Pang. (Corresponding author: Guan Gui.)
H. Huang, Y. Song, J. Yang, and G. Gui are with the Key Laboratory of
Broadband Wireless Communication and Sensor Network Technology, Nanjing
University of Posts and Telecommunications, Ministry of Education, Nanjing
210003, China (e-mail:, b14111829@njupt.edu.cn; b15080234@njupt.edu.cn;
jyang@njupt.edu.cn; guiguan@njupt.edu.cn).
F. Adachi is with the Research Organization of Electrical Communication,
Tohoku University, Sendai 980-8577, Japan (e-mail:, adachi@ecei.tohoku.
ac.jp).
Digital Object Identifier 10.1109/TVT.2019.2893928
nique for enhancing system throughput. To multiplex a large amount
of data streams and achieve more accurate beamforming in mmWave
massive MIMO, hybrid precoding was proposed [1]. In [4], a succes-
sive interference cancellation-based hybrid precoding that can realize
excellent performance with low complexity was presented, in which
the sum rate optimization problem with non-convex constraints was
divided into several sub-rate optimization issues. Then, the authors
in [5] designed a low-complexity hybrid analog/digital precoding for
multiuser mmWave systems by configuring a hybrid precoder. How-
ever, these precoding schemes proposed in the previous works have
high commotional complexity and require a complicated bit allocation
strategy since the previously proposed hybrid anlog/digital precoding
schemes are based on singular value decomposition (SVD). Addition-
ally, the newly proposed geometric mean decomposition (GMD)-based
scheme [6] can avoid the bit allocation issue, but it still brings great
challenges in addressing the non-convex constraint on the analog pre-
coder and in exploiting the structural characteristics of the mmWave
massive MIMO systems.
However, in the context of the mmWave massive MIMO systems,
though a quantity of researches have been devoted to enhancing the
hybrid precoding performance, there are still a lot of problems re-
maining and two major challenge are the extraordinarily high com-
putational complexity and poor system performance. In the past few
years, many scholars have realized this gap and they have provided
different methods for reducing the computational complexity or im-
proving the precoding performance, such as the (GMD)-based scheme
[6], the matrix factorization-based hybrid precoding mean [7], a pre-
coding method based on radio-frequency (RF) and baseband signal
processing [8], and hybrid spatial processing architecture aided pre-
coding approach [9], et al. Also, for the sake of realizing high spectrum
efficiency with low complexity, an alternating minimization scheme for
effectively designing hybrid precoder was provided [10]. Then, by ex-
ploiting low-dimensional beamspace channel state information (CSI)
processed by compressive sensing (CS) detectors, paper [11] presented
a beamspace-SVD based hybrid precoding method for reducing com-
plexity. In general, these works are based on conventional mathematical
means such as the SVD and the GMD, which are too weak to exploit
the sparsity statistics of the mmWave massive MIMO. Simultaneously,
since the traditional methods are inadequate to leverage the structural
characteristics of such mmWave systems, traditional low-complexity
schemes are realized at the cost of degrading the hybrid precoding of
the systems. Therefore, previous works fail to deal with these issues
fundamentally and new methods are urgent need to be put forward for
enhancing the hybrid precoding performance of the mmWave massive
MIMO.
Recently, the emerging solution called deep learning [12] is an ex-
traordinarily remarkable technology for handling explosive data and ad-
dressing complicated nonlinear problems. It has been proved that deep
learning is an excellent tool to deal with complex non-convex problems
and high-computation issues, which is dedicated by its super-excellent
recognition and representation abilities. Some previous works which
incorporate deep learning into communications have been investigated,
including beam selection, heterogeneous network, non-orthogonal mul-
tiple access (NOMA), massive MIMO, and heterogeneous network
[13]–[20]. Additionally, deep learning has been applied to intelligent
traffic control area [21]–[23], showing great advancements resulting
from the deep-learning-based communication schemes.
0018-9545 © 2019 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission.
See http://www.ieee.org/publications standards/publications/rights/index.html for more information.
3028
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 68, NO. 3, MARCH 2019
Thus, this study investigates a framework which integrates deep
learning into hybrid precoding in mmWave MIMO systems. The main
contributions of this paper are summarized as follows.
1) First, this is the first work to design a framework that incorporates
the deep learning technique into hybrid precoding. Specifically,
we regard a deep neural network (DNN) as an autoencoder, and
this model is regarded as a black box, where activation functions
optimize multiple layers of the network and create corresponding
mapping relations.
2) In our work, a hybrid precoding scheme based on deep learning
is provided. Here, the DNN is capable of capturing structural
information of hybrid precoding scheme through the training
stage, contributing to lowering the computational complexity.
Additionally, simulation results and comparisons have verified
the superiority of the proposed methods.
The rest of this paper is organized as follows. To begin with, we
establish a mmWave massive MIMO model, in which many antennas
are implemented at the base station (BS). Then, in Section III, to
achieve hybrid precoding with good performance, we develop a DNN
framework and provide a deep learning-enabled scheme. Simulation
results for assessing the performance of the deep learning-based method
are provided in Section IV, and conclusions are presented in Section V.
Notations: Ns is denoted as independent data streams, Nt and Nr
are defined as the transmitted antennas and the received antennas. Also,
represent RF chains. Furthermore, N is denoted as the
N R F
number of samples.
and N R F
r
t
II. SYSTEM MODEL
We consider a typical mmWave massive MIMO system, in which
one BS with a uniform linear array (ULA) of Nt antennas and user with
Nr received antennas are designed. Here, the BS sends Ns independent
data streams to the user, and it is assumed to have no information on
all the communication links. Additionally, it is assumed that the BS
RF chains, respectively, which
and the user have N R F
meet the requirements that Ns ≤ N R F
≤ Nr
[3]. Furthermore, we introduce the well-known Saleh-Valenzuela (SV)
channel model [3], and the channel matrix H ∈ CN t ×N r is written by
≤ Nt and Nt ≤ N R F
and N R F
r
r
t
t
H =
Nt Nr
P
α0at (θt
0
)ar (θr
0
) +
αp at (θt
p
)ar (θr
p
)
,
(1)
Here, P denotes the number of non-line-of-sight (NLoS) components.
Additionally, the steering vectors at (θt
) are defined as the
array responses at the BS and the user, respectively. Furthermore, θt
p
and θr
p represent the angle of departure (AoD) at the BS and the angle
of arrival (AoA) at the user, respectively. For a ULA, at (θp t ) ∈ CN t ×1
and ar (θp r ) ∈ CN r ×1 can be expressed as
) and ar (θr
p
p
P
p = 1
T
at (θt
p
ar (θr
p
) = 1√
Nt
) = 1√
Nr
−j 2π d
λ
sin θ t
p , . . . , e
−j 2π d
λ
(N t −1) sin θ t
p
1, e
,
(2)
−j 2π d
λ
1, e
sin θ r
p , . . . , e
−j 2π d
λ
(N r −1) sin θ r
p
T
,
(3)
Here, d is supposed as the antenna spacing, while the wavelength of
the carrier frequency is defined by λ. As reported in [24], H has low-
rank characteristic since the limited scattering feature in the mmWave
massive MIMO channel, indicating that near-optimal throughput is
achieved by leveraging limited amounts of RF chains.
low-dimensional digital precoder as DA ∈ CN t ×N R F
CN R F
Then, we assume a high-dimensional analog precoder and a
and DD ∈
×N s , respectively, and a hybrid decoder is denoted as D =
t
t
DA DD ∈ CN t ×N s . Hence, the transmitted signal x is given as
x = Ds = DA DD s,
(4)
where s ∈ CN s ×1
is the source signal with normalized power
E[ssH ] = IN s , and we assume that tr{DDH } ≤ Ns to satisfy the
constraint of transmit power [25]. Subsequently, the received signal
vector is defined as
y = BH Hx + BH n
D
n,
BH
A
BH
A
)HDA DD s + BH
= (BH
(5)
D
Here, n ∼ CN (0, σ2IN s
) denotes the additive white Gaussian noise
(AWGN). Additionally, BH = BH
A is a hybrid combiner, in which
BD ∈ CN R F
are defined as the digital com-
biner and the analog combiner, respectively. Note that the analog pre-
coder/combiner is always installed by analog phase shifters, and all
elements of DA and BA are supposed to meet the requirement as
BH
×N s and BA ∈ CN r ×N R F
D
r
r
|{DA}i , j| = 1√
Nt
, |{BA}i , j| = 1√
Nr
,
(6)
In mmWave massive MIMO system, fully utilizing the sparsity of the
mmWave channel can greatly enhance the performance of the hybrid
precoding [24], and thus, we employ a state-of-the-art DNN to construct
a novel precoding framework.
III. PROPOSED DEEP-LEARNING-BASED HYBRID
PRECODING SCHEME
This part provides a model in which deep learning can be adopted
in the mmWave massive MIMO for achieving end-to-end highly effi-
cient hybrid precoding. The splendid learning ability of deep learning
enables the spatial features to be exploited of the mmWave massive
MIMO system and regard the entire system as a black box to capture
useful features for hybrid precoding. We develop the proposed DNN
framework and describe how the nonlinear operation can be mapped
to the hybrid precoder, and then we provide a novel training policy for
facilitating the performance of the DNN.
A. Proposed Deep Neural Network Architecture
Recently, with the aid of deep learning, considerable process has
been achieved in a wide range of areas, including natural language pro-
cessing (NLP), computer vision (CV), automated driving, and so on.
Additionally, deep-learning-based methods can be performed by mas-
sively concurrent architectures with distributed memory architectures,
such as graphics processing units (GPUs), which have been highlighted
for their energy efficiency and impressive computational throughput,
arousing great interest in industrial communities.
Deep neural networks (DNNs), the most universal structure of deep
learning frameworks, and it can be considered as a multiple layers
perceptron (MLP). Specifically, in contrast to an conventional artificial
neural network (ANN), many hidden layers are present in a DNN to
enhance its learning and mapping abilities. In a DNN, many units are
deployed in each hidden layer, and the output can be generated based
on the output of these units with the aids of activation functions. In most
cases, the rectified linear unit (ReLU) function and the Sigmoid func-
tion are used in the nonlinear operation. Assuming a as the argument,
they are defined as ReLU(a) = max(0, a) and Sigmoid(a) = 1
1+ e−a ,
respectively. The output of the network is denoted as o and that v
denotes the input data, the mapping operation can be presented as
z = f(v, w) = f
(n−1)(f
(n−2)(· · ·f 1(v))),
(7)
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 68, NO. 3, MARCH 2019
3029
loss = R1 − RA RD F
tr((R1 − RA RD )(R1 − RA RD )H )
m i n{N t , N s }
=
(R1 − RA RD ),
δ2
i
=
i= 1
(11)
where · F denotes the Frobenius norm and RA and RD rep-
resent the GMD-based analog precoder and the GMD-based digi-
tal precoder, respectively. Additionally, Eq. (11) should satisfy the
constraint |{RA}i , j| = 1√
) ≤ Ns . More-
over, δi (R1 − RA RD ) denote the singular values of matrix (R1 −
RA RD ).
} and tr(RA RD RH
RH
A
N t
D
Next, we employ the DNN framework to construct an autoencoder,
which is given by
R1 = f(RA RD ; Ω),
(12)
f(·) denotes the mapping relation, for which the detailed training pro-
cedure is provided as follows, and Ω is defined as the dataset of the
samples.
p and AOD θt
We consider the proposed deep-learning-based scheme as a mapping
operation, and a training mechanism is formulated for extracting the
structural statistics of the mmWave-based model. First, we initialize
RA and RD as empty matrices, and then we generate random data se-
quences in the DNN. Based on different channel conditions, the DNN is
trained with the input data sequences, and RA and RD can be updated.
p can be generated
Synchronously, the physical AOA θr
randomly, and we can obtain the bias between R1 and RA RD from the
output layer of the DNN based on the input signals in different cases
through a large number of iterations. Thus, the training dataset Ω is
acquired, consisting of the structural features of the mmWave massive
MIMO model and the input data sequences, as well as the output of the
DNN. This is an unsupervised learning training approach. In the next
stage, the DNN needs to be tested after being trained thoroughly. For
each channel condition, the optimal analog precoder RA and digital
precoder RD can be obtained based on the given input signal vectors
without requiring iterations. Then, based on the proposed methhod,
the stochastic gradient descent (SGD) algorithm with momentum is
employed to process the loss function, which is given by
Rj + 1
A
Rj + 1
D
= Rj
A
= Rj
D
+ v,
+ v,
(13)
(14)
Here, v is denoted as the velocity for facilitating the gradient element.
A and R0
Additionally, the iteration number is denoted as j, and R0
D
are assumed to be the randomly generated initial solution. Specifically,
the update procedure of v can be given by
v = αv − g
= αv −
m i n{N t , N s }
(R1 − RA RD ), (15)
R A ,R D
δ2
i
i= 1
1
N
where α denotes the momentum parameter and denotes the learning
rate. Synchronously, g and N represent the gradient element and the
number of samples, respectively. Concretely, the learning framework
for super hybrid precoding is described in Algorithm 1.
In addition, to investigate the precoding performance of the deep
learning-based precoding strategy, we introduce the mean square error
(MSE) to analyze its performance, which can be given as
MSE = ER1 − RA RD 2,
(16)
Fig. 1. DNN architecture in the proposed scheme.
where n and w represent the number of layers in the neural network
and the weights of the neural network, respectively.
To realize hybrid precoding, we construct a DNN framework, as
exhibited in Fig. 1. Here, in the input layer, the length of each training
sequence is determined by its dimension, which is a fully connected
(FC) layer with 128 units for capturing features of the input data. The
next two hidden layers for processing encoding operation are also FC
layers comprising 400 units and 256 units, respectively. Following by
this, to disturb the signals with the AWGN or other distortion, a noise
layer which is consisted of 200 units for mixing distortion. Subse-
quently, for the sake of achieving decoding, we design the remaining
two hidden layers with 128 units and 64 units, respectively. In addition,
the output layer is deployed to generate expected output signals of the
network. Moreover, note that ReLU function is introduced as the acti-
vation function of the input layer and the hidden layers. However, for
enforcing the power constraint in the output layer, a special activation
is designed as
f(s) = min(max(s, 0), Ns ),
(8)
B. Learning Policy
For simplifying the mapping relation of the hybrid coding, we adopt
the GMD method to decompose the complex mmWave massive MIMO
channel matrix, and H is reformulated by
y = WQRH
= [W1, W2]
,
RH
1RH
2
∗
Q1
0 Q2
(9)
Here, W1 ∈ CN r ×N s is a semi-unitary matrix, which is regarded as
the combiner. Additionally, R1 ∈ CN t ×N s is defined as the precoder,
and it is also a semi-unitary matrix. Furthermore, Q1 ∈ CN s ×N s
is
an upper triangular matrix, while ∗ is an arbitrary matrix that can be
neglected. Specifically, the largest Ns singular values are formulated as
N s ∈ ¯q, ∀i, where qi , j represent the elements
) 1
qi , i = (δ1, δ2, . . . , δN s
in matrix Q1. Afterwards, we obtain the received signal as
y = BH Hx + BH n
= WH
1
HR1s + WH
1
n
= Q1s + WH
1
n,
(10)
To train the hybrid precoder to realize precoding, the loss function
is written as
3030
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 68, NO. 3, MARCH 2019
COMPUTATIONAL COMPLEXITY OF SEVERAL PRECODING SCHEMES OF
MMWAVE MASSIVE MIMO
TABLE I
C. Complexity Analysis
One of the key advantages of the proposed hybrid precoding mean
is that this method lowers the computational complexity. Noted that
the matrix multiplication is a Ns × N 2
t space, the complexity of the
deep-learning-based method is only O(L2Ns N 2
), achieving technical
advancement compared with that of previous researches, such as the
conventional SVD based method. To verify the low computational
complexity of the deep-learning-based scheme intuitively, we define K
as the number of users, and we present the computational complexity
of the proposed method and that of other typical precoding approaches,
which is illustrated as TABLE I.
t
Algorithm 1: DNN Based Hybrid Precoding Algorithm in
Massive MIMO.
Input: The physical AOA θr
Output: Optimized precoder R1.
1:
Initialization: The amount of iteration is initialed as j = 0
and the weight is w = 0. Meanwhile, initialize error
−7. Furthermore, we set RA = 0
threshold as τ = 10
and RD = 0.
p and AOD θt
p , environment simulator.
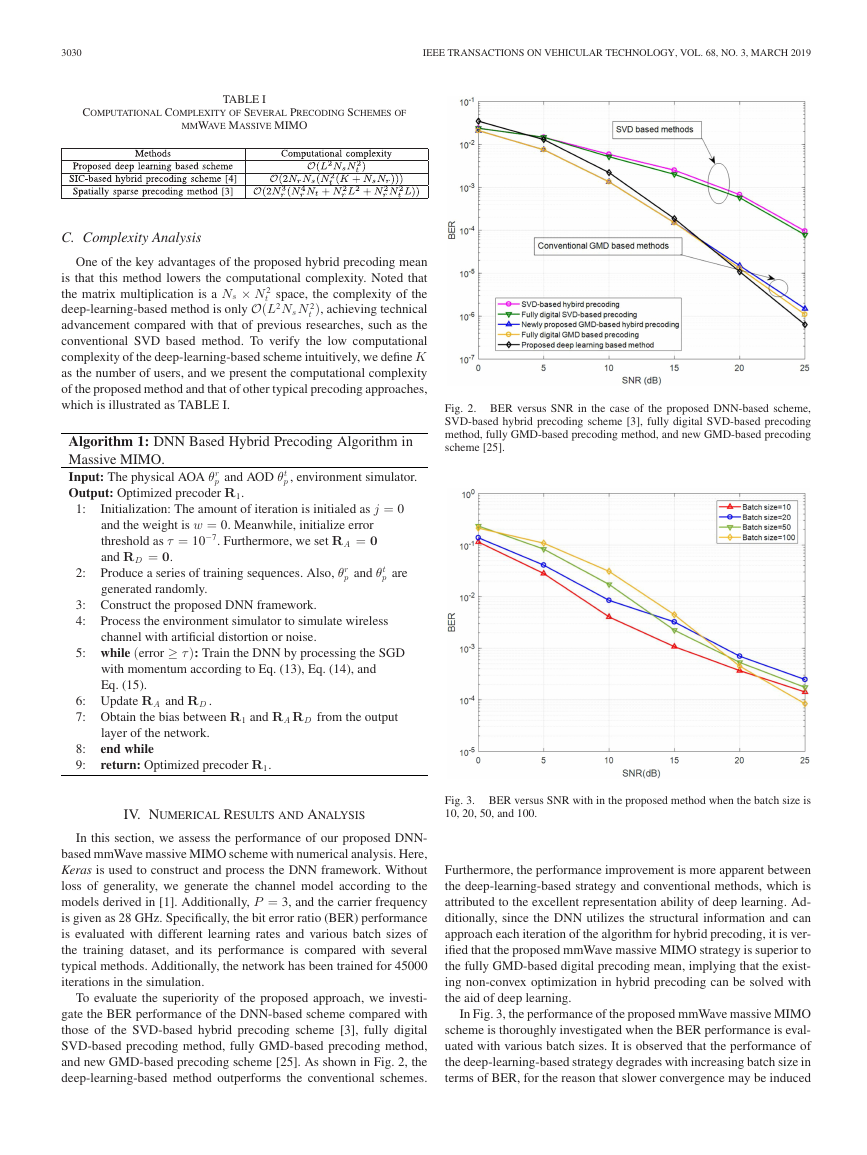
Fig. 2. BER versus SNR in the case of the proposed DNN-based scheme,
SVD-based hybrid precoding scheme [3], fully digital SVD-based precoding
method, fully GMD-based precoding method, and new GMD-based precoding
scheme [25].
2: Produce a series of training sequences. Also, θr
generated randomly.
p and θt
p are
3: Construct the proposed DNN framework.
4: Process the environment simulator to simulate wireless
5: while (error ≥ τ ): Train the DNN by processing the SGD
channel with artificial distortion or noise.
with momentum according to Eq. (13), Eq. (14), and
Eq. (15).
6: Update RA and RD .
7: Obtain the bias between R1 and RA RD from the output
layer of the network.
end while
return: Optimized precoder R1.
8:
9:
IV. NUMERICAL RESULTS AND ANALYSIS
In this section, we assess the performance of our proposed DNN-
based mmWave massive MIMO scheme with numerical analysis. Here,
Keras is used to construct and process the DNN framework. Without
loss of generality, we generate the channel model according to the
models derived in [1]. Additionally, P = 3, and the carrier frequency
is given as 28 GHz. Specifically, the bit error ratio (BER) performance
is evaluated with different learning rates and various batch sizes of
the training dataset, and its performance is compared with several
typical methods. Additionally, the network has been trained for 45000
iterations in the simulation.
To evaluate the superiority of the proposed approach, we investi-
gate the BER performance of the DNN-based scheme compared with
those of the SVD-based hybrid precoding scheme [3], fully digital
SVD-based precoding method, fully GMD-based precoding method,
and new GMD-based precoding scheme [25]. As shown in Fig. 2, the
deep-learning-based method outperforms the conventional schemes.
Fig. 3. BER versus SNR with in the proposed method when the batch size is
10, 20, 50, and 100.
Furthermore, the performance improvement is more apparent between
the deep-learning-based strategy and conventional methods, which is
attributed to the excellent representation ability of deep learning. Ad-
ditionally, since the DNN utilizes the structural information and can
approach each iteration of the algorithm for hybrid precoding, it is ver-
ified that the proposed mmWave massive MIMO strategy is superior to
the fully GMD-based digital precoding mean, implying that the exist-
ing non-convex optimization in hybrid precoding can be solved with
the aid of deep learning.
In Fig. 3, the performance of the proposed mmWave massive MIMO
scheme is thoroughly investigated when the BER performance is eval-
uated with various batch sizes. It is observed that the performance of
the deep-learning-based strategy degrades with increasing batch size in
terms of BER, for the reason that slower convergence may be induced
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 68, NO. 3, MARCH 2019
3031
Fig. 4. BER performance versus SNR in the proposed method with various
learning rates.
Fig. 6. MSE versus iterations in the case of the deep learning-based method,
the analog precoding approach, and the sparse precoding method.
precoding method [3], and the fully digital GMD based precoding
scheme. As shown in Fig. 5, we observe that the spectrum efficiency is
improving as the SNR increases in all the schemes. Also, it can be seen
from Fig. 5 that the proposed hybrid precoding scheme outperforms
other strategies, which achieves better hybrid precoding performance
dedicated by the excellent mapping and learning capacities of the deep
learning. Furthermore, when the SNR increases, the performance gap
of the deep learning based scheme and that of other approaches is
becoming larger. This superior performance further demonstrates the
effectiveness of the proposed hybrid precoding scheme.
Finally, for the purpose of investigating the robustness and stability
of the proposed hybrid precoding approach, we explore the relationship
between the MSE and the iterations of the deep learning-based strategy
compared with the analog precoding scheme, and the sparse precoding
method. Here, the learning rate is set as 0.001. As can be seen from
Fig. 6, we observe that the MSE performance is stirred with the increas-
ing iterations, which is dedicated by the fact that all these algorithms
are approaching to conversion with more iterations. Also, it can be
seen from Fig. 6 that the proposed deep learning based scheme and the
sparse precoding method both convert at around 11 iterations, whereas
the analog precoding scheme requires about 22 iterations. Furthermore,
we can further observe that the MSE performance of the proposed deep
learning based scheme is superior than that of other means. Hence, it
comes to a conclusion that the proposed deep learning-based approach
realizes superior performance in terms of the hybrid precoding accu-
racy and conversion compared to other schemes.
V. CONCLUSIONS
In this paper, we considered a super approach in enhancing the hy-
brid precoding performance, including cutting down the computational
complexity and leveraging the spatial statistics of the large antenna sys-
tems in mmWave massive MIMO scenario. We first provided a detailed
deep-learning-based hybrid precoding method. Analytical results were
presented to verify the performance of the DNN-based method, reveal-
ing that the DNN can facilitate the hybrid precoding because of its
great recognition and mapping abilities. Another promising direction
is to apply deep learning in the channel feedback issue to alleviate the
issues related to codebook size and feedback overhead.
Fig. 5.
Spectrum efficiency versus SNR in the case of the proposed deep
learning based hybrid precoding scheme, the spatially sparse precoding method
[3], and the fully digital GMD based precoding scheme.
by a larger batch size. However, we further observe that too small
batch size will lead to unstable convergence. Therefore, it is noted
that we should choose batch size carefully for achieving the optimal
performance in the proposed precoding mean.
Fig. 4 presents the BER versus SNR in the DNN-based mmWave
massive MIMO scheme with different learning rates. It can be wit-
nessed in Fig. 4 that the performance of hybrid precoding in the DNN-
based method is optimized by adopting a lower learning rate, which
occurs because a larger learning rate causes a higher validation error.
Note, however, that slower convergence behavior will be induced by
using a lower learning rate, though it does enhance the system perfor-
mance. Hence, in order to realize better performance, how to select
the best learning rate is an open issue in the proposed framework for
hybrid precoding.
In Fig. 5, we show the spectrum efficiency performance against the
SNR of the DNN-based hybrid precoding scheme, the spatially sparse
3032
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 68, NO. 3, MARCH 2019
REFERENCES
[1] A. Ghosh et al., “Millimeter-wave enhanced local area systems: A high-
data-rate approach for future wireless networks,” IEEE J. Sel. Areas Com-
mun., vol. 32, no. 6, pp. 1152–1163, Jun. 2014.
[2] T. Rappaport et al., “Millimeter wave mobile communications for 5G
cellular: It will work,” IEEE Access, vol. 1, pp. 335–349, May 2013.
[3] O. E. Ayach, S. Rajagopal, S. Abu-Surra, Z. Pi, and R. W. Heath, “Spa-
tially sparse precoding in millimeter wave MIMO systems,” IEEE Trans.
Wireless Commun., vol. 13, no. 3, pp. 1499–1513, Mar. 2014.
[4] X. Gao, L. Dai, S. Han, C.-L. I, and R. W. Heath, “Energy-efficient
hybrid analog and digital precoding for mmWave MIMO systems with
large antenna arrays,” IEEE J. Sel. Areas Commun., vol. 34, no. 4,
pp. 998–1009, Apr. 2016.
[5] A. Alkhateeb, G. Leus, and R. W. Heath, “Limited feedback hybrid pre-
coding for multi-user millimeter wave systems,” IEEE Trans. Wireless
Commun., vol. 14, no. 11, pp. 6481–6494, Nov. 2015.
[6] C. E. Chen, Y.-C. Tsai, and C.-H. Yang, “An iterative geometric mean de-
composition algorithm for MIMO communications systems,” IEEE Trans.
Wireless Commun., vol. 14, no. 1, pp. 343–352, Jan. 2015.
[7] J. Jin, Y. R. Zheng, W. Chen, and C. Xiao, “Hybrid precoding for millimeter
wave MIMO systems: A matrix factorization approach,” IEEE Trans.
Wireless Commun., vol. 17, no. 5, pp. 3327–3339, May 2018.
[8] E. Zhang and C. Huang, “On achieving optimal rate of digital precoder
by RF-baseband codesign for MIMO systems,” in Proc. IEEE 80th Veh.
Technol. Conf., Vancouver, BC, Canada, Sep. 2014, pp. 1–5.
[9] G. Wang and G. Ascheid, “Joint pre-/post-processing design for large
millimeter wave hybrid spatial processing systems,” in Proc. Eur. Wireless
Conf., Barcelona, Spain, May 2014, pp. 1–6.
[10] X. Yu, J.-C. Shen, J. Zhang, and K. B. Letaief, “Alternating minimiza-
tion algorithms for hybrid precoding in millimeter wave MIMO sys-
tems,” IEEE J. Sel. Topics Signal Process., vol. 10, no. 3, pp. 485–500,
Apr. 2016.
[11] C. H. Chen, C.-R. Tsai, Y.-H. Liu, W.-L. Hung, and A.-Y. Wu, “Com-
pressive sensing assisted low-complexity beamspace hybrid precoding for
millimeter-wave MIMO systems,” IEEE Trans. Signal Process., vol. 65,
no. 6, pp. 1412–1424, Mar. 2017.
[12] G. E. Hinton, S. Osindero, and Y. W. Teh, “A fast learning algorithm for
deep belief nets,” Neural Comput., vol. 18, pp. 1527–1554, 2006.
[13] F. Tang et al., “On removing routing protocol from future wireless net-
works: A real-time deep learning approach for intelligent traffic control,”
IEEE Wireless Commun., vol. 25, no. 1, pp. 154–160, Feb. 2018.
[14] N. Kato et al., “The deep learning vision for heterogeneous network traf-
fic control: Proposal, challenges, and future perspective,” IEEE Wireless
Commun., vol. 24, no. 3, pp. 146–153, Jun. 2017.
[15] B. Mao
et al., “Routing or computing? The paradigm shift
to-
wards intelligent computer network packet transmission based on deep
learning,” IEEE Trans. Comput., vol. 66, no. 11, pp. 1946–1960,
Nov. 2017.
[16] G. Gui, H. Huang, Y. Song, and H. Sari, “Deep learning for an effec-
tive non-orthogonal multiple access scheme,” IEEE Trans. Veh. Technol.,
vol. 67, no. 9, pp. 8440–8450, Sep. 2018.
[17] H. Huang, J. Yang, H. Huang, Y. Song, and G. Gui, “Deep learning for
super-resolution channel estimation and DOA estimation based massive
MIMO system,” IEEE Trans. Veh. Technol., vol. 67, no. 9, pp. 8549–8560,
Sep. 2018.
[18] H. Huang, G. Gui, H. Sari, and F. Adachi, “Deep learning for super-
resolution DOA estimation in massive MIMO systems,” in Proc. Veh.
Technol. Conf., Chicago, IL, USA, Aug. 2018, pp. 1–6.
[19] H. Huang et al., “Unsupervised learning based beamforming design for
downlink MIMO,” IEEE Access, vol. 7, pp. 7599–7605, Jan. 2019.
[20] M. Liu, T. Song, J. Hu, J. Yang, and G. Gui, “Deep learning-inspired
message passing algorithm for efficient resource allocation in cognitive
radio networks,” IEEE Trans. Veh. Technol., vol. 68, no. 1, pp. 641–653,
Jan. 2019.
[21] F. Tang, Z. M. Fadlullah, B. Mao, and N. Kato, “An intelligent traf-
fic load prediction based adaptive channel assignment algorithm in
SDN-IoT: A deep learning approach,” IEEE Internet Things J., vol. 5,
no. 6, pp. 5141–5154, Dec. 2018.
[22] Z. M. Fadlullah et al., “State-of-the-art deep learning: Evolving ma-
chine intelligence toward tomorrow’s intelligent network traffic control
systems,” IEEE Commun. Surveys Tut., vol. 19, no. 4, pp. 2432–2455,
May 2017.
[23] H. Guo, J. Liu, J. Zhang, W. Sun, and N. Kato, “Mobile-edge computation
offloading for ultra-dense IoT networks,” IEEE Internet Things J., vol. 5,
no. 6, pp. 4977–4988, Dec. 2018.
[24] Z. Gao, L. Dai, D. Mi, Z. Wang, M. A. Imran, and M. Z. Shakir, “Mmwave
massive-MIMO-based wireless Backhaul for the 5G ultradense network,”
IEEE Wireless Commun., vol. 22, no. 5, pp. 13–21, Oct. 2015.
[25] T. Xie et al., “Geometric mean decomposition based hybrid precoding
for mmWave massive MIMO systems,” China Commun., vol. 15, no. 5,
pp. 229–238, May 2018.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
