强制对流和自然对流作用下枝晶生长的数值模拟 .pdf-资料库

强制对流和自然对流作用下枝晶生长的数值模拟1 http://www.paper.edu.cn 孙东科，朱鸣芳，杨朝蓉，潘诗琰，戴挺东南大学江苏省先进金属材料高技术研究重点实验室, 南京 (211189) E-mail：zhumf@seu.edu.cn 摘要：本文建立了一个基于格子玻尔兹曼方法 (lattice Boltzmann method, LBM) 的二维模型, 对强制对流和自然对流作用下合金凝固过程中的枝晶生长行为进行了模拟研究. 与传统的基于求解 Navier-Stokes (NS) 方程计算流场的方法不同, 本模型采用基于分子动理论的 LBM 对凝固过程中的传输现象进行数值计算. 用三组粒子分布函数分别建立了计算流场、由对流和扩散所控制的浓度场和温度场的 LBM 演化方程. 通过求解 LBM 演化方程获得固/ 液界面前沿的浓度和温度分布. 然后, 基于 Zhu 和 Stefanescu (ZS) 提出的溶质平衡方法计算枝晶生长的驱动力. 为了对模型进行验证, 将模拟的在强制和自然对流作用下枝晶上游尖端的稳态生长特征分别与 Oseen-Ivantsov 解析解和修正的 Lipton-Glicksman-Kurz (LGK) 模型的预测结果进行了比较. 模拟结果和理论预测结果获得了良好的吻合. 此外, 将本模型与基于 NS 方程求解流场的 ZS-NS 模型的模拟结果进行了对比, 发现两个数值模型模拟的固相分数演变曲线相接近. 表明用 LBM 计算的三传现象收敛于传统的传输模型. 同时还发现, 与 ZS-NS 模型相比, 本模型具有更好的数值稳定性和更高的计算效率. 关键词：微观组织模拟；枝晶生长；对流；格子玻尔兹曼方法中图分类号：TG244, O242 1. 引言金属凝固过程中熔体对流将直接影响最终凝固组织尤其是枝晶组织的形貌. 近年来，国内外学者针对纯金属和合金，应用相场法 (phase field, PF)[1-2]、水平集法 (level set method)[3] 或元胞自动机法 (cellular automaton, CA)[4-5]耦合基于求解 Navier-Stokes (NS) 方程的流场计算方法模拟研究了对流作用下枝晶的生长规律. 传统计算流体力学方法从连续介质假设出发, 对 Navier-Stokes 方程和连续性方程进行离散求解, 获得流场的分布及变化规律，该方法适合处理单相流问题. 而在凝固过程中存在固、液两相, 当固相分数较大时, 不能满足连续介质的假设条件而使流场计算不易收敛, 计算效率低. 格子玻尔兹曼方法(Lattice Boltzmann Method, LBM)[6-8]是近年来迅速发展起来的一种新的流体力学数值计算方法. 与传统方法不同, LBM 基于微观动力学模型来模拟复杂的宏观传输现象. 该方法具有算法简单、计算效率高、数值稳定性好、本质并行、易于处理外力源项和任意复杂的边界问题等许多传统方法无法比拟的独特优势. 近年来 LBM 已在多元流、多相流、多孔介质流、磁流体动力学等众多领域中都得到了比较成功的应用[8-9]. 并在凝固领域也逐渐得到了应用[10-11]. 但关于应用 LBM 模拟合金在对流作用下枝晶生长规律方面的报道还较少. Zhu 和 Stefanescu (ZS) 提出了一个基于界面溶质平衡思想计算枝晶生长动力学的方法 [12]. 该方法不需界面动力学系数，并具有良好的定量模拟能力. 本文用 LBM 计算凝固过程中的流场、温度场和浓度场, 并与计算枝晶生长的 ZS 方法进行耦合, 建立了一个二维的 ZS-LBM 模型, 对合金凝固过程中在强制和自然对流作用下单枝晶和多枝晶的生长规律进行模拟研究. 2. 模型与算法 1国家自然科学基金（批准号：50671025）, 江苏省自然科学基金(批准号：BK2006105), 高等学校博士学科点专项科研基金(批准号：20070286021) 资助的课题 - 1 -

http://www.paper.edu.cn 本文所建立的耦合模型主要针对二元合金在小 Peclet 数和低 Reynolds 数条件下的对流枝晶生长. 通过 LBM 计算凝固过程中合金熔体的流动、温度和浓度的分布和变化. 然后基于界面温度、浓度和曲率计算枝晶生长的驱动力. 主要控制方程和算法介绍如下. 2.1 计算传输过程的 LBM 模型与传统的计算流体力学的建模思想不同, LBM 将流体抽象为由大量虚拟粒子所组成的集合体. 这些虚拟粒子按一定的方式在离散格子上进行碰撞和迁移演化而形成了流体的宏观流动现象. 在 LBM 中虚拟粒子的数量用分布函数表示, 通过在满足一定对称条件的网格中对玻尔兹曼方程进行离散, 得到描述虚拟粒子运动规律的演化方程, 流体的密度和速度等宏观物理量可由分布函数计算得到 . 本文采用基于单松弛时间的 LBGK (lattice Bhatnagar-Gross-Krook) 方法的 LBM 模型[6, 13-14]. 计算流场的 LBGK 演化方程为 x t ),( (1) 式中, fi (x, t) 为粒子分布函数, 表示在某个时间 t、位置 x 处粒子出现的概率; ei 是粒子在 i Fi x 为力方向的速度; ∆t 是时间步长; τ 为松弛时间; 的源项, 表示流体粒子间的相互作用力或外部场力. LBM 也可应用于计算受对流和扩散控制的浓度场和温度场变化[7,14], 其演化方程为 x 表示粒子平衡分布函数; t ),( −∆+∆+ t ),( x t ),( x t ),( ex [ −= τ + f eq i x ,( /)] tt , F i − ) ( eq f t f t f f i i i i i t t ( t ) t ) g g g g − − + eq i tt , tt , G i /)] /)] τ D x ,( x ,( h eq i i h i i h i [ −= [ −= ex x t ),( x t ),( t ),( x t ),( x t ),( x t ),( i ex −∆+∆+ i h ( i i x 和 t g eq ),( (2) (3) −∆+∆+ i i x 分别表示浓度和温度的分布函数; τD 和 τα 为对应的单步松弛时间; heq 其中, Gi(x,t) 和Hi(x,t) 分别为枝晶生长过程中由溶质再分配和凝固潜热释放而产生的源项. 本文采用 D2Q9 格式计算流场、浓度场和温度场. 其离散的粒子速度可表示为 i ,0 = i ,41 −= i ,85 −= i ])2/ )1 sin[( π − i )9 sin[( 2 π − ⎧ )0,0( ⎪ i )1 (cos[( π − ⎨ ⎪ i )9 2 (cos[( − ⎩ (4) ],2/ π c ])4/ x t ),( ],4/ ατ H + = 2 e c i i 式中, c=∆x/∆t 为格子速度, ∆x 为空间步长. 流体的宏观物理量如流体密度 ρ, 流动速度 u, 浓度 C, 以及温度 T, 可分别由相应的粒子分布函数求出: if (5) ρ = 8 0i ∑ = e f i i 0 uρ 8 i = ∑ = C = T = t ∆+ F 2 (6) 8 0i ∑ = ∑ = 8 0i ig ih (7) (8) 其中, F 为液相浮力. 根据 Boussinesq 近似，浮力项中的密度 ρ 为温度梯度和浓度梯度的线性函数. 因此产生自然对流的浮力可写为 TT ( − 0 (9) 式中 ρ0 为流体当温度 T0, 浓度 C0 时的密度, g 为重力加速度, βC 和 βT 分别为由浓度和温度变化引起的流体膨胀系数. 对于 D2Q9 格式, 式(1)-(3)中粒子平衡分布函数可表示为 g βρ C CC ( gF βρ T − + = ) ) 0 0 0 - 2 -

http://www.paper.edu.cn i 2 4 2 2 2 2 4 ⋅ ⋅ ⋅ ⋅ t f eq ) ) ) ) c c c g = + + − u 5.1 (5.4 (5.4 ue i ue i eq i h eq i ) t ) = ) t ue i ue i ( x , ( x , ( x , [ w (31 = ρ + i [ Cw (31 + i [ Tw (31 + i ]2 (10) c ]2 (11) ]2 (12) c 式(11)和(12)中包含流体速度 u 的项反映了液相流动对溶质和热传输的影响. 很显然, 当 u=0 时对流作用消失, 式(2)、(3)、(11)和(12)成为描述纯扩散条件下的溶质和热量传输的 LBM 模型. 对于 D2Q9 模型, 式(1)中的外力源项可表示为 u − c 2 (13) ue i ue i eue ⋅ i c 4 1 ) 2 τ x t ),( F ∆⋅ (5.4 5.1 5.1 w i 3[ F i 1( u u − − + − = + 9 c c c c e ) ) ] t ⋅ ⋅ 2 2 4 2 2 i i 式(10)-式(13)中的 wi 为权重系数,有 w0=4/9,w1-4=1/9,w5-8=1/36. 根据 Chapman-Enskog 分析, 流体动力学黏度 ν, 溶质扩散系数 D 以及热扩散系数α, 可分别通过与之相对应的松弛时间 τ、τD 和τα 求出: t ∆= t ∆= t ∆= cD 6/)1 6/)1 6/)1 − τ α ν 2( 2( ，和 − − c c . 2 2 2 2( ατ τ D 2.2 计算枝晶生长的 ZS 模型 lC 可由下式计算 C C 本文采用 ZS 模型[12]计算枝晶的生长动力学. 在 ZS 方法中, 将固/液界面上液相的平衡浓度和实际浓度之差作为枝晶生长的驱动力. 根据液/固界面的热力学平衡关系, 界面的液相平衡浓度 * ] m ] ) ) [ ( T l ) s 0 * eq ∂ ∂ = + − + − − 2 xy K T l ε ( 1 15 ΓK [ 4 cos ( θθ 0 [ 2 ∂= ϕϕϕ x s lT 为界面温度, * (14) * l lT 为初始浓度 C0 合金的平衡熔点, ε 为界面张力各向异性强度, m 为 eq 式中, 液相线斜率, Γ 为 Gibbs-Thomson 系数, θ0 为枝晶生长择优取向与水平方向夹角, K 为固/液界面曲率, θ 为界面法向与水平方向的夹角. K 和θ可由界面处固相分数梯度进行计算 ) ϕ s y (15) (16) * 和实际液相成分 *与实际液相成分 Cl 比较. 在任一界 , 该界面网格的固相分数就增加. 根据界面的溶质平 Cl. 用式(14)后可计算获得局部界面平衡成分 Cl 面网格上, 如果满足衡条件, 在一个时间步长 ∆t 内, 界面网格内增加的固相分数 ∆φs 可由下式计算通过 LBM 模型计算流场、温度场和浓度场, 可得到局部界面温度 Tl ϕϕ s x ϕϕ y s )2/12 ] CC =∆ *, 将 Cl ] [ ( ∂⋅ arccos l C * − ( ∂+ ( ∂+ ( ∂− ( ∂− ϕ s y ϕ s x ϕ s x ϕ s x θ [ ( 2/3 − ( > = ] 0 ∂ ∂ ∂ ∂ 2 y ) ) ) ) ) 2 x 2 2 2 2 2 y s s s l 其中 k 为溶质分配系数. 根据固相分数增量, 由 V n ∆φs=(Cl * −Cl)/[Cl * (1−k)] (17) 可计算界面的生长速度. t ∆∆⋅∆= ϕ x s 假定界面上固/液相成份服从 Cs=kCl. 随着固相分数的增加, 在一个时间步长内界面上释放出的溶质和潜热分别为 ∆C=∆φsCl(1−k)和 ∆T=∆φs∆H/Cp，其中 ∆H 为凝固潜热, Cp 为热容. 因此, 式(2)和(3)中的源项可分别由以下式子计算 Gi(x,t)=wi∆φsCl(1−k) (18) Hi(x,t)=wi∆φs∆H/C (19) - 3 -

http://www.paper.edu.cn 2.3 边界条件本文所考虑的计算区域为一个二维正方形方腔 {(x, y) | 0≤x≤L, 0≤y≤L}.当模拟强制对流情况时, 过冷熔体从方腔左侧以恒速流入: u(x, y)|x=0=(Uin,0); 从右侧流出: ∂xux|x=L=0. 对流场入/出口边界均采用具有二阶计算精度的非平衡态外推法[15]处理. 用周期性边界条件处理计算区域的上下两侧边界. 当模拟自然对流情况时, 将计算区域四周视为固壁边界, 采用反弹格式处理. 浓度场的计算采用无扩散的边界条件: ∂xC|x=0, L=0, ∂yC|y=0, L=0. 此外, 由于固相不存在对流且固相中溶质扩散速度远小于液相, 本文忽略了固相中的溶质传输. 流场和浓度场均采用反弹格式处理固/液界面的无滑移边界条件. 由于固相和液相热扩散系数非常接近, 简化处理为两者相等. 计算区域的四个边界温度设定为常数 T0, 采用非平衡外推方法处理. 3. 模拟结果与讨论 3.1 扩散控制生长首先, 通过模拟受扩散控制的晶体平界面生长过程, 验证本模型对纯扩散条件下受扩散控制凝固问题的模拟能力. 晶体平界面生长是一类典型的有解析解的运动边界问题. 其界面满足 stefen 边界条件, 即 CD C i−=∇ ( 1 ) dx i dt (20) 参照文献[16]中的方法, 可得一维平界面生长时固相分数与扩散系数 D、时间 t 之间关系的解析解为 (21) 其中, φ0 为初始固相分数; λ 为常数, 本文中与 Gibbs-Thomson 系数、界面动力学系数、界面溶质分配系数 k 等有关. 图 1 为在一维平界面晶体生长时固相分数随时间变化的模拟结果与解析解的比较. 由图可见两者吻合良好. Dtλϕϕ + = 0 6 , / % ϕ0 4 − ϕ 数分相固 2 5 3 1 解析结果模拟结果 0 0 1 2 时间, t/s 3 4 图 1 模拟的受扩散控制一维平界面晶体生长固相分数随时间变化与解析解的比较 3.2 自然对流作用下单枝晶的生长由温度梯度和浓度梯度所引起的自然对流可用温度 Rayleigh 数 RaT≡gβT∆TRaL3/(να)和浓度 Rayleigh 数 RaC≡gβC∆CRaL3/(νD) 两个无量纲准数来进行描述, 其中, ∆TRa 和 ∆CRa 分别是液相中最大温度差和最大浓度差. 为了模拟自然对流作用下单枝晶的生长规律, 将计算区域 - 4 -

http://www.paper.edu.cn ε=0.0267, ∆H=5×103J/m3, Γ=6.62×10-8m·K, 剖分成 400×400 网格 , 网格尺寸取为 ∆x=0.5µm. 计算中各参数取为 : k=0.103, Cp=1937.5J/(m3·K), m=−2.16K/(wt%), ν=6.0×10-9m2/s, D=1.0×10-9m2/s, α=3.0×10-9m2/s. 无量纲 Rayleigh 数取为 RaC=RaT=5×103. 图 2 为初始过冷度∆T=0.8K 和成分 C0=0.6wt%时二元合金在纯扩散和自然对流条件下单枝晶生长形貌. 从图中可以看出, 自然对流的存在打破了枝晶生长的对称性. 这是因为枝晶生长过程中固/液界面上排出的溶质和释放的潜热形成了凝固前沿的温度和浓度梯度, 在重力的作用下就引起自然对流, 如图 2 中(c)和(d)所示. 液相流动改变了温度场和浓度场的分布, 从而对枝晶生长形貌产生了很大影响, 迎流方向的生长得到了促进, 而顺流方向的生长受到了抑制. 此外, 当枝晶生长到相同的固相分数 φS=0.1 时, 自然对流作用下所需的凝固时间为 0.162s. 比纯扩散条件下所需的凝固时间(0.168s)略短. 这是因为自然对流的存在加快了溶质和热量在熔体内的传输速度. (a) (b) (c) (d) 图 2 过冷熔体中二元合金单枝晶生长形貌模拟结果 ∆T=0.8K, C0=0.6wt% 纯扩散条件下: (a) 浓度场; (b) 温度场. 自然对流作用下: (c) 浓度场; (d) 温度场. 为了进一步定量研究自然对流对枝晶生长的影响, 分别将自然对流作用下和纯扩散条件下枝晶尖端生长速度(Vtip)随时间变化的模拟计算结果进行了分析. 将沿垂直向下、垂直向上和水平方向生长的枝晶尖端分别定义为上游尖端、下游尖端和水平尖端. 图 3 为模拟的各尖端速度随时间变化. 由图 3(a)可知, 凝固初期枝晶所有尖端都以一个较快的速度生长. 随着生长的进行, 固/液界面上释放出溶质和凝固潜热, 导致枝晶尖端前沿的温度和浓度的增加, 如图 3(b)和(c)所示. 因此, 尖端生长速度迅速下降. 经过一段时间, 溶质和潜热在界面前沿的释放与由对流和扩散的传输基本达到平衡, 使生长速度达到了大致的稳态值. 上游尖端的稳态生长速度最高, 下游尖端的稳态生长速度最低, 而水平尖端介于两者之间, 与纯扩 - 5 -

http://www.paper.edu.cn 散的情况大致相当. 由于上游尖端生长快, 释放出溶质多于下游, 尽管有对流的作用, 上游尖端的浓度仍略高于下游尖端浓度, 如图 3(c)所示. 而由尖端温度和曲率所确定的尖端平衡浓度的上游值与下游值之间相差更大, 使得上游的( 大于下游, 如图 3(d)所示. 根据式(17)可知上游尖端的固相分数增量大于下游尖端. 因此, 上游尖端生长速度高于下游尖端. CCC − ) * l * l l 100 10 1 s / m 4 − 0 1 / p i t V , 度速长生端尖上游下游水平无流动 329.6 Κ T / , 度温端尖 329.5 329.4 329.3 329.2 上游下游水平无流动 0.8 1.0 1.2 0.1 0.0 0.2 0.4 0.6 时间, t/s 0.8 1.0 1.2 329.1 0.0 0.2 0.4 0.6 时间, t/s (a) (b) 1.4 0 1.3 l C / C , 度浓际实端尖 1.2 1.1 1.0 0.9 上游下游水平无流动 0.0 0.2 0.4 0.6 时间, t/s ) * l C 2 - 0 1 ( / ) l C - * l C ( , 度浓衡平端尖 1.0 0.8 0.6 0.4 0.2 0.0 0.0 0.2 0.4 0.8 1.0 1.2 上游下游水平无流动 0.8 1.0 1.2 0.6 时间, t/s (c) (d) 图 3 对应于图 2 中枝晶尖端生长速度、温度、实际浓度和平衡浓度与时间的关系: (a) 尖端生长速度; (b) 尖端温度; (c) 尖端实际浓度; (d) 尖端平衡浓度. P T T C P T =Ω eP π T 为验证本模型对自然对流作用下枝晶生长的模拟, 我们参考文献[17]推导出包含对流作用的修正二维 Ivantsov 解，即考虑对流作用时二维的无量纲温度过冷度 TΩ 和浓度过饱和度 CΩ 可由以下式子计算 ( 21+ ( 21+ ( ( erfc ( ( erfc )R ) ) (22) ) )R ) (23) 式中, PT≡VR/(2α) 和 Pc≡VR/(2D) 分别是温度和浓度 Peclet 数; δT 和 δC 分别是温度和浓度边界层厚度; R 和 V 分别是枝晶尖端半径和尖端生长速度. 参照 Li 和 Beckermann 在文献[18] 中的方法, 将修正的 Ivantsov 解代入二维 Lipton-Glicksman-Kurz (LGK) 模型的过冷度计算中, 从而得到计算自然对流作用下枝晶生长的解析模型 Tk Ω∆ e C ( ) k 1 Ω−− (24) erfc ( ( erfc ) − ) eP π C T =∆ =Ω L C Γ R δ C δ T P C P C P T − + 1 P C ⎞ +Ω⎟⎟ ⎠ T ⎛ ⎜⎜ ⎝ C P - 6 -

http://www.paper.edu.cn ( 110 − )k T =∆ e mC 式中为平衡凝固温度区间. 表 1 为不同初始成分时, 用本模型模拟得到的上游枝晶尖端的稳态生长速度和半径与解析解的比较, 其中尖端半径用文献[12]所描述的方法计算. 从表 1 可以看出, 随着初始浓度的增加, 两种模型得出的尖端稳态生长速度和半径的变化趋势相同, 吻合较好. 表 1 自然对流作用下不同初始成分时上游枝晶尖端稳态生长速度和半径的模拟结果与理论预测结果的比较初始成分 C0 / wt% 生长速度 / 10-5m/s 尖端半径 / 10-6m 理论值模拟值理论值模拟值 ( ∆T=0.8K) 0.4 9.149 8.868 2.121 1.712 0.5 8.209 6.446 2.087 1.668 0.6 7.446 5.764 2.063 1.661 0.7 6.816 5.158 2.045 1.635 3.3 强制对流作用下单枝晶的生长在强制对流条件下枝晶生长的模拟中, 忽略重力对液相流动的影响. 因此, 将式(1)中的外力源项设为 Fi(x,t)=0. 流场的初速度由流入区域的液相所产生, 其入口速度为 Uin. 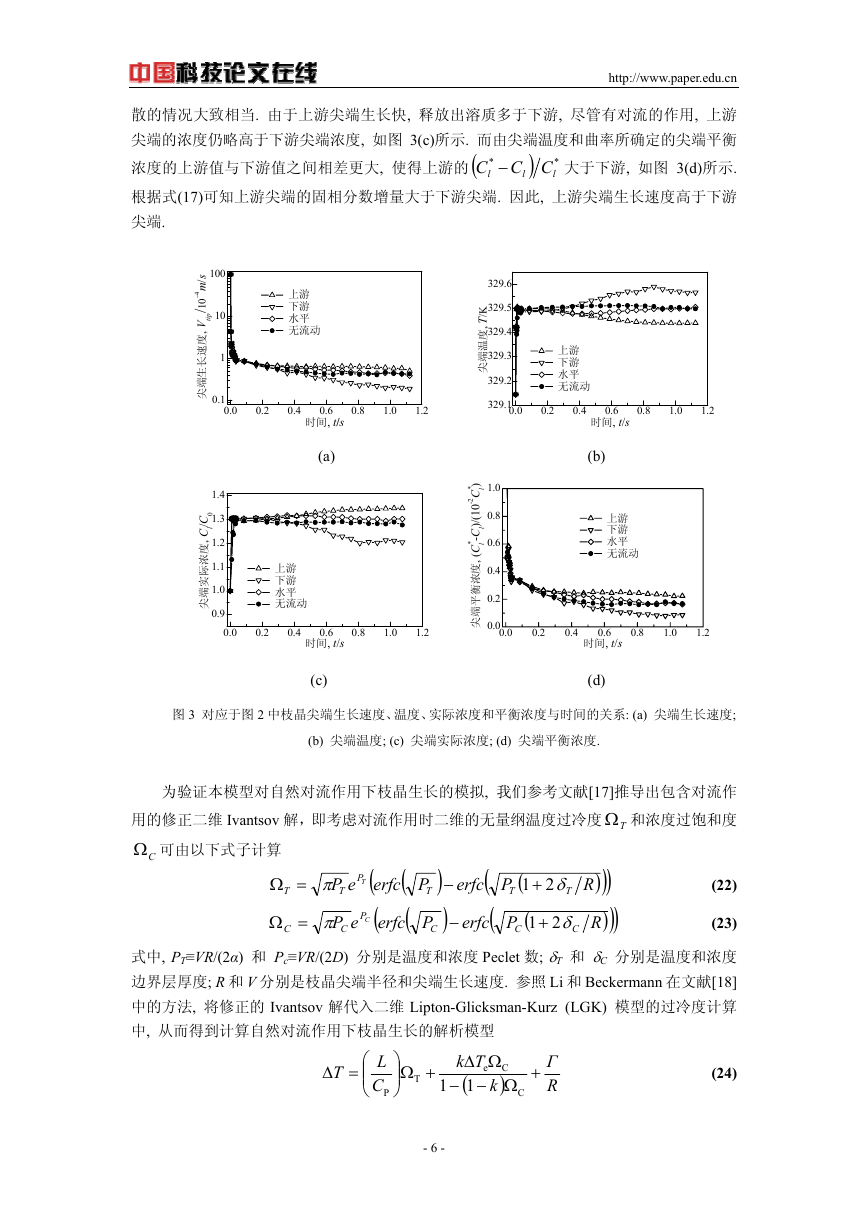由于 Al-Cu 合金的热扩散系数比溶质扩散系数大 4 个数量级, 其枝晶生长动力学受溶质传输所控制. 为了简化, 假定区域中温度均匀恒定. 图 4 为模拟的 Al-7wt%Cu 合金在过冷度∆T=4K 和入口流速 Uin=0.001m/s 时单枝晶的生长形貌. 计算区域为 300×300 网格, 格子尺寸为 0.3µm. 合金的物性参数取自文献[4]. 从图 4 可以看出, 与自然对流的情况相似, 强制对流的存在也破坏了枝晶生长的对称性, 上游枝晶臂的生长较为发达, 而在下游方向的生长受到了抑制. 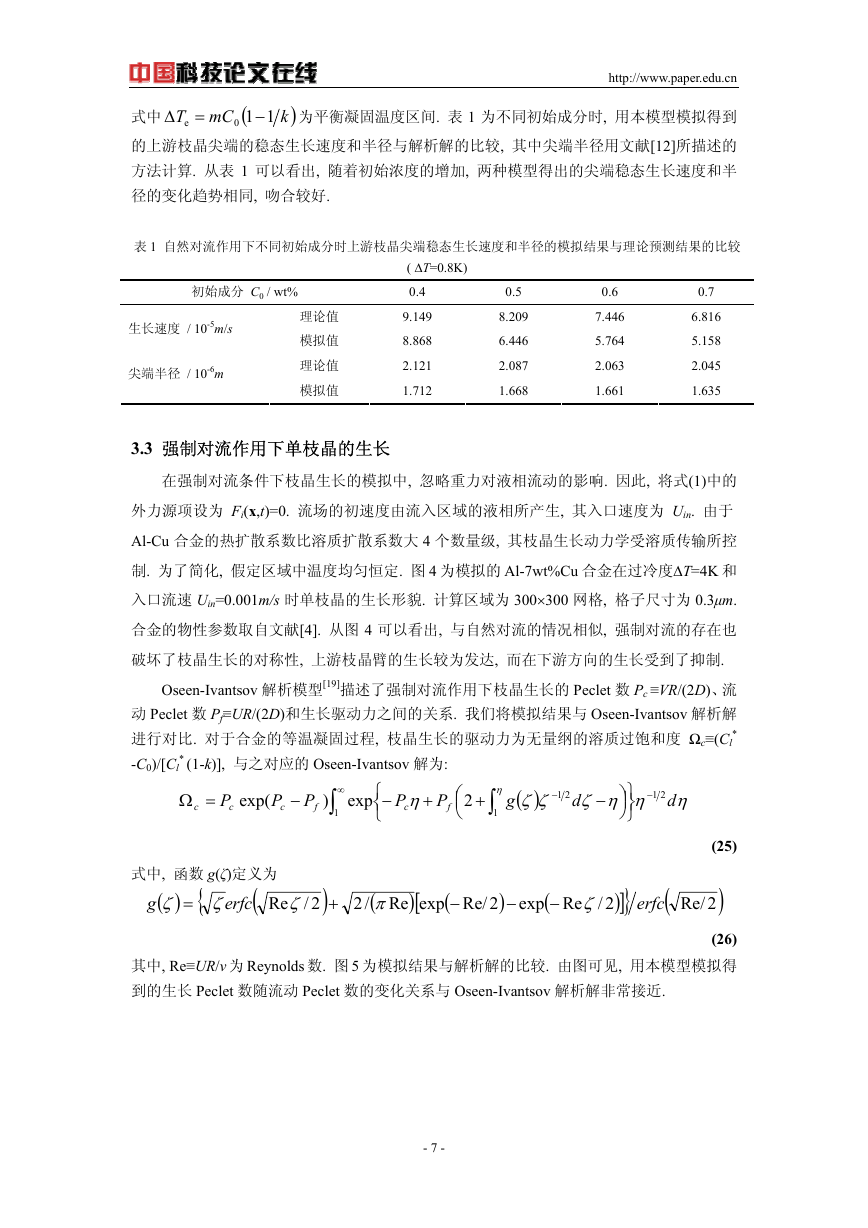Oseen-Ivantsov 解析模型[19]描述了强制对流作用下枝晶生长的 Peclet 数 Pc ≡VR/(2D)、流动 Peclet 数 Pf≡UR/(2D)和生长驱动力之间的关系. 我们将模拟结果与 Oseen-Ivantsov 解析解 * 进行对比. 对于合金的等温凝固过程, 枝晶生长的驱动力为无量纲的溶质过饱和度 Ωc≡(Cl -C0)/[Cl * (1-k)], 与之对应的 Oseen-Ivantsov 解为: =Ω c P c exp( P c − P f ) ∞ ∫ 1 exp ⎧ ⎨ ⎩ − P + η c P f 2 + ⎛ ⎜ ⎝ η ∫ 1 g ( ηηηζζζ 21 − 21 − − d d ) ⎞ ⎟ ⎠ ⎫ ⎬ ⎭ (25) g = ( 式中, 函数 g(ζ)定义为 ) + { ζ /2 Re ( π erfc ( ) ζ 2/Re ζ [ ( ) exp − )2Re/ (26) 其中, Re≡UR/ν 为 Reynolds 数. 图 5 为模拟结果与解析解的比较. 由图可见, 用本模型模拟得到的生长 Peclet 数随流动 Peclet 数的变化关系与 Oseen-Ivantsov 解析解非常接近. 2/Re ( exp − 2Re/ erfc } ] ) ) − ζ ( - 7 -

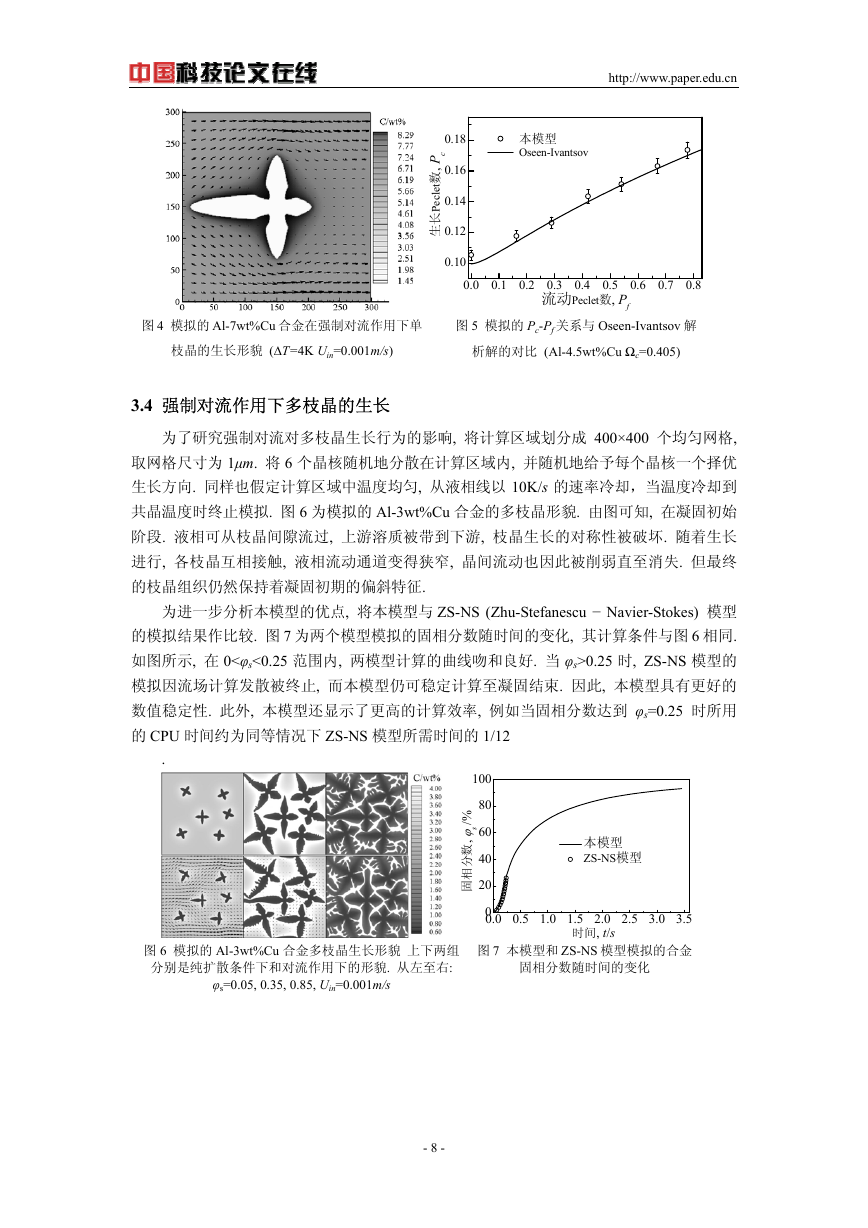
http://www.paper.edu.cn 本模型 Oseen-Ivantsov c P , 数 t e l c e P 长生 0.18 0.16 0.14 0.12 0.10 图 4 模拟的 Al-7wt%Cu 合金在强制对流作用下单枝晶的生长形貌 (∆T=4K Uin=0.001m/s) 3.4 强制对流作用下多枝晶的生长 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 流动Peclet数, Pf 图 5 模拟的 Pc-Pf 关系与 Oseen-Ivantsov 解析解的对比 (Al-4.5wt%Cu Ωc=0.405) 为了研究强制对流对多枝晶生长行为的影响, 将计算区域划分成 400×400 个均匀网格, 取网格尺寸为 1µm. 将 6 个晶核随机地分散在计算区域内, 并随机地给予每个晶核一个择优生长方向. 同样也假定计算区域中温度均匀, 从液相线以 10K/s 的速率冷却，当温度冷却到共晶温度时终止模拟. 图 6 为模拟的 Al-3wt%Cu 合金的多枝晶形貌. 由图可知, 在凝固初始阶段. 液相可从枝晶间隙流过, 上游溶质被带到下游, 枝晶生长的对称性被破坏. 随着生长进行, 各枝晶互相接触, 液相流动通道变得狭窄, 晶间流动也因此被削弱直至消失. 但最终的枝晶组织仍然保持着凝固初期的偏斜特征. 为进一步分析本模型的优点, 将本模型与 ZS-NS (Zhu-Stefanescu − Navier-Stokes) 模型的模拟结果作比较. 图 7 为两个模型模拟的固相分数随时间的变化, 其计算条件与图 6 相同. 如图所示, 在 0<φs<0.25 范围内, 两模型计算的曲线吻和良好. 当 φs>0.25 时, ZS-NS 模型的模拟因流场计算发散被终止, 而本模型仍可稳定计算至凝固结束. 因此, 本模型具有更好的数值稳定性. 此外, 本模型还显示了更高的计算效率, 例如当固相分数达到 φs=0.25 时所用的 CPU 时间约为同等情况下 ZS-NS 模型所需时间的 1/12 . 100 80 60 40 20 本模型 ZS-NS模型 / , % ϕs 数分相固图 6 模拟的 Al-3wt%Cu 合金多枝晶生长形貌上下两组分别是纯扩散条件下和对流作用下的形貌. 从左至右: φs=0.05, 0.35, 0.85, Uin=0.001m/s 0 0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 时间, t/s 图 7 本模型和 ZS-NS 模型模拟的合金固相分数随时间的变化 - 8 -

资料库

强制对流和自然对流作用下枝晶生长的数值模拟 .pdf

相关推荐

开发技术

热门标签

最新资料