论文研究-资产流动性优化管理系统的设计与实现.pdf-资料库

年 ! 月系统工程理论与实践第 ! 期资产流动性优化管理系统的设计与实现凌晓东一刘萍 ∀中信国际研究所 , 北京 # # # # ∃ % ∀北京科技大学计算机系 , # # # & ! % 摘要本文介绍一种金融机构风险资产流动性优化管理的决策支持系统 ∋ 该系统以金融理 ∗ +, 〕〕− ∗ ) 为平台加以实论为依据 , 建立了债券组合的利率风险免疫模型 , 并以 ( ) 现 ∋ 借助于电子表格的优良特性 , 该系统将初始数据的获得、数据的修改与处理 , 以及优化、仿真分析联系在一起 , 使用十分方便 · 最后 , 说明了系统的应用和可能的扩展 · 关健词资产流动性管理债券组合利率风险免疫非线性规划一 . / 0 1 23 4 5 4 6 78 9 70 8 0 4: 5 : 2; 4 ; < = 2> ? 26 2: ≅ − Α: 28 2Β 5: 2; 4 ) ≅ 1 :0 8 = 24 3 Χ 25 ; 6 ; 4 3 ∀Δ +Ε +Δ Φ0 10 5 Γ 0 Η +4 : 0 Γ 4 5 : 2; 4 5 7 , Δ Η24 5 +4: 0 Γ 4 5 : 2; 4 5 7 升 ? 1 : 5 4 6 +4Ι0 ϑ 0 2Κ24 3 # # # # ∃ % 1 : 8 0 4 : Δ ; 印; Γ 5 : 2; 4 , = 2? Α 24 3 ∀ϑ 0 2Κ24 3 Λ 4 2Ι0 Γ 1 2:≅ ; < ) 0 20 4 0 0 5 4 6 Ε0 0 Η 4 ; 7; 3 叭 # # # & ! % Ε Η 21 Α5 Α0 Γ 9 Γ 0 1 0 4 : 1 5 6 0 0 21 2; 4 1 ? 9 9 ; Γ: 1 ≅ 1 : 0 8 ; < 72> ? 26 2:≅ 8 5 4 Ν ϑ 5 1 0 6 ; 4 : Η 0 8 ; 6 0 Γ 4 <2 4 5 4 0 257 :Η 0 ; Γ ≅ :Ο; Γ 21 Π 28 8? 4 2Β 5: 2; 4 <; Γ Μ ; 4 6 Α ; Γ :<; 72; Ο0 Γ 0 ) ; 8 0 Γ 0 75 : 0 6 ? 26 2:≅ 8 5 4 5 3 0 8 0 77: Ρ Μ ; 4 6 9 ; Γ : <; 72; Ρ 24: 0 Γ 0 1 : Ρ 4 ; 4 724 0 5 Γ ΑΓ ; 3 Γ 5 8 8 24 3 ; Α : 28 2Β 5: 2; 4 ∋ 一 Γ 5: 0 Γ 21Π 28 8 ?Ν 一Γ 5 : 0 ∗ +, / − ∗ ) ∋ , 引言金融机构运作的一个基本特点是负债经营 ‘ 由负债偿还的性质决定 , 相当一类金融机构在资产安排时必须考虑负债的偿还 ∋ 比如 , 商业银行必须准备现金以应付客户提取到期的存款 , 或支付债券的利息和本金 Ρ 养老基金必须定期为退休者支付养老金 Ρ 保险公司必须赔偿投保人符合保单规定的事故损失 Ρ 开放式共同基金必须保证投资人随时赎回自己的受益凭证 ∋ 于是 , 这些金融机构在追求较高的投资收益的同时必须考虑负债偿还数量与期限结构 , 以便为偿还债务提供及时而足够的现金流 ∋ 就要求这些金融机构的部分或全部资产具有足够的流动性, 即保证随时以正常的市值转化为现金一种通常的做法就是根据负债偿还的性质 , 将全部资产或其中的一部分建立一个债券组合 ∋ 这 ∋ 债券与其它金融资产 ∀比如说股票 % 的主要区别是其带来的现金流可以由较为规则的方式事先确 ∋ 比如信用债券和抵押债券 , 都可以在到期日之前按固定利率定期得到利定 , 或说具有较小的风险 # 本文于 Σ 年 ! 月 Τ & 日收到 ∋

系统工程理论与实践年 ! 月息 , 并在到期日得到本金 ∋ 人们选择债券作为保持流动性的工具不仅是因为它们具有较小的风险 , 而且因为它们品种繁多 , 具有不同的到期期限 , 而且发行量和交易量巨大 , 足以为投资者形成一个保证流动性的 “ 缓冲垫 ” ∋ 在世界金融市场 Υ = , 每年都要发行数千亿美元的债券类资产 , 其发行额和交易额大约占世界交易总量的 # ς ∋ 在债券组合面对的诸多风险中 , 利率风险是资产流动性管理所要对付的主要风险 ∋ 比如 , 尽管负债愕还的时间和数量是已知的, 但负债的现值却是不确定的当市场利率发生变化 , 负债的贴现率就会发生变化负债的现值也跟着变化如果市场利率变化引起资产市值下降而未能引起负啧市值的相应下降 , 这时又有到期负债需要偿还 , 就会发生流动性的困难 ∋ 所以 , 如何回避利率风险, 是债券组 · 合管理的主要目标之一所谓流动性管理犷就是确保债券组合免受利率波动的影响融理论为基础 , 讨论金融机构资产流动性优化管理系统的研制与应用 , 相信它对中国金融机构的资产 ∋ 本文将以现代金优化管理具有借鉴作用 ∋ Τ 利率风险免疫系统的基本模型所谓免疫的债券组合是指在某一时期内, 保持债券组合的收益率恒等于所要求的水平 , 从而使 ∋ 从理论上说 , 利率风险免疫可以有两类方法 , 即现金流量债券组合的市值不受市场利率变动的影响匹配方法和持续期限方法 ∋ 现金流量匹配是一种直观和简便易行的方法 , 它的基本思路是根据每一笔一的确定关系负债的偿还时间与数量 , 购买与之价值相同且到期日相同的债券 , 从而在资产与负债之间建立一对 , 于是 , 随着负债偿还时间的到达 , 债券的利息和本金将依次用于负债的偿还 ∋ 这就是说 , 现金流量匹配的债券组合一经确定之后 , 不管利率如何变动 , 不需重新调整, 便可确保到期负债的偿还 ∋ 但这种方法也有明显的缺点 ∋ 一方面 , 为了做到现金流量匹配 , 就要找到期限、数量恰好一致的债券 , 而这往往与资产收益的目标相矛盾 ∋ 有时为了满足前者 , 不得不放弃一些更具有吸引力的债券 ∋ 另一方面 , 现金流量匹配的债券组合一旦建立 , 不能根据情况变化加以调整 , 这意味着持有这种僵硬的债券组合要使用较多的资金 ∋ 与现金流量匹配方法不同 , 持续期限方法不要求资产与负债的一一对应 , 因而可以在较低的成本下实现免疫 ∋ 本文主要讨论基于持续期限方法的两种模型 ∋ · Τ 持续期限模型 ∀ % 持续期限方法的基本思路是平衡利率变动对债券投资的双重影响根据金融理论 , 利率风险包一方面 , 当市场利率提高时 , 将引起债券市值下降 , 导致资本损失 , 给投括价格风险和再投资风险 ∋ ∋ 资者带来价格风险 ∋ 但利率的提高也可以给投资者带来更多的再投资收益 ∋ 另一方面 , 利率的下降将导致较低的再投资收益 , 这投资者带来所谓的再投资风险 ∋ 但利率下降也可以使债券市值上升 , 带来资本收益 ∋ 可见 , 不管上升还是下降 , 利率的每一种变动都会给债券持有者同时带来正面和负面的影 , 通过调整债券组合这里 , 问题的关键是需要权衡 , 以了解这种变动的净效应如何人们发现 77Ω ∋ ∋ 响的持续期限 , 使上述正负效应恰好相抵 , 就可以避免利率变化对债券组合价值的影响 ∋ 于是 , 为了在投资期内实现债券组合的免疫 , 投资经理的任务就是调整和控制债券组合的持续期限及分散度 , 抵消利率变化对债券市值的影响 , 保证到期负债的还本付息 ∋ 以下给出上述过程的严格描述 ∋ 假设可供选择的债券有 ( 种 ∋ 为 ∀Ξ Ε ( %、, 现值为 ∀Α Ψ %, Δ ∀: , 动, 可得到整个债券组合的现金流 Δ ∀:% , 购买数量为 ΚΨ2 ∋ 第乞种债券的在投资期带来的现金流为 Δ 以, 动, 到期收益率通过合并所有债券的同期现金流 , 得到债券组合的现值 ∀尸 Ψ %Ρ 和到期收益根据公式 ∀7% , Τ , … , 人< , 艺 Ζ ∋

第 ! 期资产流动性优化管理系统的设计与实现率 ∀Ξ Ε ( %9 ∋ ∀9 Ι% , 一艺州9 Ι%2 艺Ζ , ∀尸Ι% , Ν Δ ∀云% 菩7石亩氖丽其中几 Ζ 8 5 [ ∴双 ] , 双是债券 ‘ 的到期时间 · 债券葱和债券组合的持续期限定义为双艺倒 · 亡 Δ ∀亡, 乞% ⊥ _ ∀Ξ Ε ( %、Ω‘ ∀Α Ψ %‘ ∀/ 二二%‘ 一几艺倒 · : Δ ∀艺% 【 _ ∀Ξ Ε ( %, 」‘ ∀Α Ψ %9 ∀/ 。 ⎯ %, Ζ ∀% ∀Τ % 容易看出 , 债券的持续期限是这个债券给持有者带来的现金流的平均时间 , 债券组合的持续期限是这个债券组合给持有者带来的现金流的平均时间、进一步的分析可以证明 , 这个平均时间就是债券市值关于利率变动改变率的一阶近似 , 因而可以用来作为债券所面对的利率风险的估计值 ∋ 于是 , 为了保证到期债务的偿还 , 必须使债券组合与负债的市值对利率变动做出一致的反映 , 即保持债券组合的持续期限等于负债的偿还时间 ∋ 当然 , 在多重负债偿还的情形下 , 仅仅这一条件还是不够的 · 还要考虑债券组合带来的现金流与负债偿还的现金流的分散程度 ∋ 假设负债偿还的数量为 = ∀:% , 云二 , Τ , … , 几 ∋ 债券组合分散度和负债现金流分散度分别定义为「丝 ‘/ ‘“, 一 7馨β∀/ ”尹 , 艺一 ∀/ “Γ , ·,丫(」 , ∀/ ‘“, 一 ∴谷“一 ∀/ ” Γ , · 7丫几 , 飞‘α Τ 「竺 , ’α Τ ‘! , 其中 ∀/ 。 ⎯ %= 是负债流的持续期限 , 其定义与债券持续期限的定义类似示债券组合现金流和负债偿还现金流对于它们的均值 ∀ 即持续期限% 的平均偏离证每一笔到期债务的偿还 , 债券组合的分散度应大于或等于负债的分散度 ∋ · ∀/ 艺、%, 与 ∀/ 乞, %= 分别表容易看出 , 为了保 ∋ 上面的持续期限条件和分散度条件刻划了资产与负债两方面现金流在时间上的对应 , 还要考虑数量上的对应 , 所以 , 为了保证到期债务的偿还 , 债券组合的现值应大于或等于负债的现值 ∋ 即 ∀9 Ψ %, 全 ∀9 Ψ %二 ∀∃ % , 在以上条件 ∀Τ % 以表示成以下非线性规划 ⎯ ∀! % , ∀∃ % 的约束下 , 寻求具有最大收益率的债券组合 ∴,7 77 5 Χ ∀Ξ Ε ( %, ∀/ 。 ⎯ %, 三 ∀/ 。二%⎯ ∀/ 艺1 %Ρ 全 ∀/ 乞1 %Ρ ∀9 Ψ %Ρ 全 ∀9 Ψ %⎯ , 从 , … , 刃五了 ] 的问题 , 可 ∀Σ % 、其中 ∀Ξ Ε ( %, Τ∋ ∀/ 。 , %9 Τ 持续期限模型 ∀Τ % 、 ∀/ 、 Γ %Ρ 、 ∀/ 乞1 %, 、 ∀/ 乞1 %⎯ 、 ∀9 Ψ %, 、 ∀9 Ψ %⎯ 的定义已如前述 · 持续期限模型 ∀7% 中的持续期限条件、分散度条件和现值条件对任意方式的利率变化进行免疫 ∋ 比如 , 它假定利率曲线的变但是 , 这些条件对实现债券组合的免疫并不是充分的 ⊥ΒΩ 都是必要的 ∋

系统工程理论与实践年 ! 月化是平行的 , 无法对利率曲线的任意变化进行免疫 ∋ 一旦利率曲线不以这种方式变化 , 债券组合对利率变动并不免疫 ∋ 于是存在一种可能 , 即使前面三个条件都得到满足 , 该债券组合仍不能保证到期负 ∋ 于是需要克服以上局限性 , 建立适应任意利率曲线变化的债券组合免疫模型债的还本付息和 Ι5 12 δ0 Π 证明 ⊥1Ω 函数 , 对于投资经理来说它是外在的 , 不可控的 Ρ 另一项的大小则与如何组合债券有关 , 因而是可控 , 债券组合市值水平的变动的界可以表示为两项因素的乘积 χ; 4 3 其中一项是利率的 ∋ ∋ ∋ 的于是 , 可以通过调整债券的组合来减小后一因子 , 以降低债券组合市值的不利变动 , 达到免疫的这个可控的因子称为风险免疫指标 ∋ 目的 ∋ 风险免疫指标的债券组合 ∴,7 上问题 , 我们得到债券组合免疫模型 ∀Τ %⎯ 从 , , … , , ( ] 根据以上讨论 , 我们的问题可以概括为寻求一个具有最小 , 并同时满足前面三个条件 ∋ 用一个非线性规划表示以 +4 74 +Φ ( ∀/ , %, 三 ∀/ 二 %= ∀/ 乞1 %, 全 ∀/ ￡1 %⎯ ∀9 Ψ %, 七 ∀9 Ψ %⎯ ∀ % 其中 + Φ ( 为风险免疫指标 , 几 +Φ ( 一艺尸 Ψ Δ 引 ‘一 ∀玩⎯ 川α ∀尸Ι% , 几艺曰尸 Ψ = ε β‘一 ∀/ 二 ⎯ %9 7α ∀9 Ψ %, , 尸 Ψ Δ χ: 是第 ‘期现金流入的现值 , Α Ψ = , 是第 : 期负债支付的现值 , ∀/ 二 ⎯ %Ρ 、 ∀/ 二 ⎯ %⎯ 、 ∀/ 该1 %, 、 ∀/ 乞。%⎯ 、 ∀尸Ψ %, 、 ∀尸Ψ %= 的定义同持续期限模型 ∀7% 应当注意的是以上两个持续期限模型适 · 用条件的区别 ⎯ 持续期限模型 ∀7% 仅在利率曲线平行变化或利率变化较小的情形下有效 , 而持续期限模型 ∀Τ % 可以保证对利率曲线的任意变化免疫 ∋ ! 模型的数值实现及算例上述模型计算中两个基础性概念是债券组合收益率和债券组合的持续期限 , 前者表示债券组合整体收益水平 , 后者则近似地度量债 ∋ 在一些券组合在该收益水平下所面对的风险文献中四 , 作者想当然地用个别债券收益率和持续期限的加权平均来计算债券组合的收益率和持续期限 , 从而得到对应于 ∀Σ % 和 ∀ % ∋ 但是 , 用这种简单方法得到的结和线性规划打打开备选债券数据和负债流数据据设设定决策变量单元及初值值调调用函数模块计算债券组合合的的现金流 Δ ∀:% 和收益率 ∀Ξ Ε ( %999 计计算债券组合的 ∀尸 Ψ %, 计计算负债流的 ∀尸 Ψ %= 、、 ∀/ 。劝, ∀/ 二动= 、、 ∀/ 坛, %,, ∀/ 乞1% === 设设定目标函数单元及约束单元元调调用 ) ;7 Ι0 Γ 加载宏求解规划划果是错误的 ∋ 正确的方法是 , 通过合并所有债生生成当前求解结果报表及现金匹配状态图形形券的同期现金流来计算整个债券组合的现金流 , 再得到债券组合收益率和持续期限 ∋ 图 ) ;7 Ι 0Γ 模块运行流程图然而 , 按合并现金流的方式计算债券组合的收益率和持续期限将增加规划问题的非线性性质 ∋ 并且 , 由于 ∀Ξ Ε ( %, 是以隐函数形式表示 , 数学规划中的目标函数和约束条件也只能用隐函数方式

第 ! 期资产流动性优化管理系统的设计与实现 φ φ 一)山一γ门一习口一一,一山巨口一!二一山∀∀乏丑赎赎黯翻氰氰蒸蒸蒸喊喊喊一一飞飞 #∃ %&∋( ∗∗∗∗∗ 一一飞飞 + + + 一一一一呼呼于飞飞杯甲两两漏漏翱嘛蘸续妇蜘蘸毓橇橇橇橇瘾棒藕藕骊熏熏二二一一 ∀∀∀∀∀入. ,,, ∀∀∀∀∀∀尸 , ∀∀∀∀∀的 , 月 ∀∀∀∀∀寸 −−− ∀∀∀∀∀刹图 / 娜五男务随目俗叫截 )困

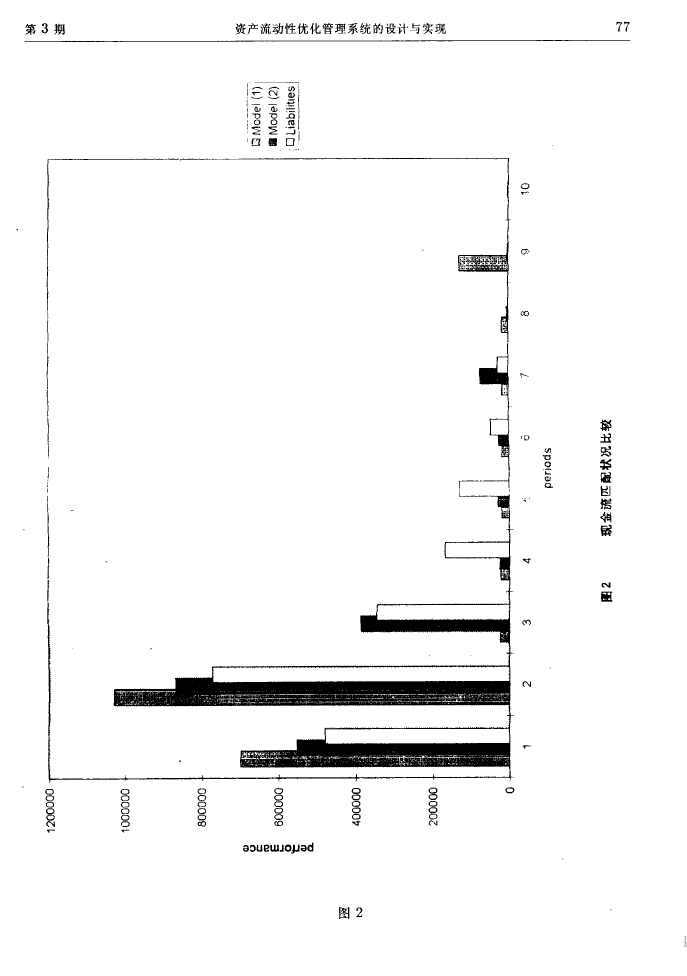
系统工程理论与实践年 ! 月写出 , 给规划求解带来麻烦 , 为此 , 我们以 ( ) 一η [ δ0 7 电子表格为系统开发工具 , 解决了以上问题 ∋ 图是利率风险免疫系统中 ) ;7 Ι 0Γ 模块运行的流程图 ∋ ∋ 例根据以上方法 , 我们用持续期限模型 ∀7% 和 ∀Τ % 计算一个具有 ! 种债券、为了保证多样性 , 我们限制对每种债券的投资不得超过债券组合市值的三分之一表是输入图 Τ 是在两种模型下对负债流支付状况的比较 ∋ 其中 , 债券组 ∋ 容易看出 , 两种模型所使用的资金数量相同 , 但 ∀7% 比 ∀Τ % φ 期负债支付流的算合带来的现金流与负债流均以现值表示数据 , 表 Τ 是两种模型的计算结果 ∋ 有更高的收益率 , 而 ∀Τ % 比 ∀7% 有更好的现金流匹配效果 ∋ 债债券序号号到到期时间间 Τ ! & ∃ & Σ φ ! φ & Τ # Τ Σ Τ ∃ !!! ### 票票面利率 ∀ς %%% ∋ ! ∃ & ∋ Σ Τ ∋ φ ∋ Σ Τ ∋ ∃ Σ ! ∋ ∃ ∋ ∃ ! ∋ ∃ !!! 债债券面值 ∀元%%% Σ # # Σ # # Σ# # # # # # # # Σ # # ∋ Σ # # # # # # # # Σ # # Σ # # Σ # # Σ # ### 债债券价格 ∀元 %%% ∃ & ∃ & # ∃ φ # Τ# # ∃ # ∃ φΣ ! Τ# ∃ & φ ∃ ∃ ∃ # ∃ φ ### 负负债流 ∀元%%% Σ # # # # # & Σ # # # # ∃ # ## # # Τ # # # # & # # # φ &# # Σ # ### 债债券序号号模模型 ∀ %%% ! # Σ ∋ ! Τ # 模模型 ∀Τ %%% &∃ ∋ ∃ ∋ ! # ! ∃ # ∃ Σ # # φ # ∋ & Σ Τ ∋ & & ∃ Τ Σ & # Τ !!! ∃ ∃ ∋ ∋ Τ Τ ∋ Σ # ! Σ ∋ # # ∃ φ ∋ Σ ! ∋ ∃ ! # ### ∃∃∃ ∀9 Ψ %, ⎯ ∀%Ζ & Σ ∀Τ %Ζ & Σ ∀Ξ Ε ( %9 ⎯ ∀ %Ζ & ∋ # ς ∀Τ %Ζ ∋ ! ς 由于 ( ) 一η [ δ0 7 可以与其它不同数据格式的系统进行数据交换 , 故本系统可以方便地获取并使并且 , 调入 η [ δ0 7 中分析工具加载宏 , 用户另外 , 由于 η [ δ0 7 对不同工作表或同一工作用其它 ∗ 24 6 ;Ο 1 与非 ∗ 24 6 ;Ο 1 应用软件建立的数据 ∋ 可以对输入数据和优化结果进行各种统计处理和分析 ∋ 表间各单元格的动态连接 , 用户可以随意变动初始数据单元格的内容 , 其余相关变量单元格的内容也将按照设定的公式或调用的函数关系自动改变 , 而不必人为修改中间的计算过程 ∋ 于是 , 通过调用一 7< 加载宏 , 用户可以方便地改变债券个数和债券参数、改变负债流的长度和数量、或施加任何 ∗ Η 5: 附加的约束 , 对各种假设情形进行仿真分析 ∋ ∃ 结语 ∋ 为了保证债券组合对利率风险免疫 , 持续期限理论要求在整个投资期内保持持续期限条件、分散度条件和现值条件 ∋ 因此 , 债券组合的不断调整是必需的 ∋ 这种调整将相应地增加监测成本和交易成本 ∋ ∋ Τ 如果在持续期限方法的基础上引入预期因素并允许其在决策中发挥作用 , 就可以利用期货与期权手段来维持持续期限条件、分散度条件和现值条件 ⊥17 ∋ 但是 , 究竟在多大程度上采用这种较为积极的债券管理 , 将取决于负债的性质 , 也取决于投资经理在得到信息与做出决策方面的能力 ∋ 在

第 ! 期资产流动性优化管理系统的设计与实现这方面 , 持续期限方法的派生物有所谓的弹性免疫 ∀δ; 4: 24 30 4: +8 8 ? 4 2Β 5: 2; 4% 和混合免疫 ∀8 2[ 0 6 28 8? 4 2Β 5: 2; 4 % ∋ ! ∋ 本文讨论的风险免疫模型假定了确定性的负债支付流 , 这对商业银行和养老基金等一类金融机构的风险资产的流动性管理是适用的 ∋ 对随机的负债支付流 , 如保险公司对随机发生的事故赔偿损失的支付 , 则需在估计概率分布的基础上用随机优化模型予以考虑 ∋ ∋ ∃ 对于一个由不同国家货币标价的债券构成的组合来说 , 由于国际金融市场实行浮动汇率制 , 汇率变动将对以外币标价的债券价值发生影响 ∋ 因此 , 流动性管理中还必须考虑可能的汇率波动对债券组合带来的风险 ∋ χ 5 Μ ; Β Β 2 χ ι ∋ ϑ ; 4 6 ( 5 ΓΠ 0 : 1 , . 4 5 7≅ 121 5 2 2 6 ) : Γ 5: 0 3 20 1 ∋ / − ∗ ι − , η ) 一+Φ ∗ +, , ! ∋ 参考文献 ι; 4 5: Η 5 4 η ∋ ) : 0 Α Η 0 4 . Φ ∋ / ? Γ5 : 2; 4 5 4 6 ( 0 5 1 ? Γ0 扭0 4 : ; < ϑ 5 1 21 Φ 21 Π ∋ ι54 ? 5 Γ ≅ φ Ψ 5 1 70 0 Π # ∋ ∋ ∋ . Φ 21 Π ( 24 28 Β 24 3 ): Γ 5: 0 3 ≅ <; Γ ( ? 7:29 70 = 25Μ 272: ≅ ι ; ?ΝΓ 4 5 7 ; < χ24 5 4 0 0 , / 0 0 0 8 Μ 0 Γ &∃ ∋ ∋ ι ; Η 4 Δ Δ ι ; ? Γ 4 5 7 ; < ϑ ? 1 24 0 1 1 , χ; 4 3 ϕ Α 0 5Γ 1 ; 4 Δ +8 8 ? 4 2Β 5 :2; 4 ∋ χΓ 5 4 0 21 ι Δ ∋ ∋ ∋ κ ; Ο 0 / ( Τ ∋ +4 Ι 0 1 :8 0 4: 1 ⎯ . 4 5 7≅ 1 21 5 4 6 ( 5 4 53 0 8 0 4 : 一Γ 5 : 0 Φ 21 Π . ϕ ? 26 0 : ; ( 5 4 5 3 24 3 +4: 0 Γ0 1 : ∋ ∋ 一 ∋ , Η277 ( 0 ϕ Γ 5Ο , 0 Ο Ξ; Γ Π +4 1 : 2: ? : 0 ; < χ24 5 4 0 0 , ∀上接第页% 即证得对任 ∗ 〔几 , 必有 Δ Λ ∀∗ % 三 ( ∀∗ % ∋ 即证得 Δ Λ ∀∗ % 是入的经典精确最优置信上限 ∋ 参考文献 ∗ 24: ; Γ Μ ; : : ; 8 8 257 ) ? Μ 1 ≅ 1 : 0 8 / 5 : 5 ∋ . , ∋ , ι ∋ . 8 0 Γ ∋ ) : 5 : 21 ∋ . 1 1 ; 0 ∋ , φ∃ , ∋ = − , Ι 0 Γ Δ ; 4 <2 6 0 4 0 0 = 28 2: 1 <; Γ ) 0 Γ 20 1 ) ≅ 1 : 0 8 Φ 0 725 Μ 272: ≅ <Γ ; 8 ϑ 24 ; Ν 范大茵 · 对成败型元件串联系统可靠性置信下限 = Α 排序法的改进 ∋ 浙江大学学报 , & , ∋ ∋ ∋ ϑ ? 0 Η 70 Γ , Φ ; < : Η 0 . 8 0 Γ 20 5 4 ) : 5 : 21 : 20 5 7 . 1 1 ; 0 25 : 2; 4 , Σ φ ι ∋ , Τ Δ ; 4 <2 6 0 4 0 0 728 2: 1 <; Γ : Η 0 Α Γ ; 6 ? 0 : ; < Ε Ο ; ϑ 24 ; 8 25 7 Α 5 Γ 5 8 0 : 0 Γ 1 ∋ ι; ? Γ 4 5 7 郑海鹰 ∋ 排序法计算指数寿命型元件串联系统可靠性经典精确最优置信下限 ! , & ∀Τ % · ∋ 高校应用数学学报 ,

资料库

论文研究-资产流动性优化管理系统的设计与实现.pdf

相关推荐

开发技术

热门标签

最新资料