176 2015，51（6） Computer Engineering and Applications 计算机工程与应用 具有颜色保真性的快速多尺度 Retinex 去雾算法 肖胜笔，李 燕 XIAO Shengbi, LI Yan 暨南大学 信息科学技术学院 计算机科学系，广州 510632 Department of Computer Science, College of Information Science and Technology, Jinan University, Guangzhou 510632, China XIAO Shengbi, LI Yan. Fast multiscale Retinex algorithm of image haze removal with color fidelity. Computer Engi- neering and Applications, 2015, 51（6）：176-180. Abstract：The multiscale Retinex algorithm has some drawbacks in the application of image haze removal, such as color distortion and high computation cost. A fast multiscale Retinex algorithm of image haze removal with color fidelity is pro- posed. Instead of processing three color channels, the proposed algorithm only processes on the dark channel, which avoids the influence on the tone correlation and reduces the running time. Experimental results are presented to demon- strate the performance of the proposed algorithm. Key words：image haze removal; color fidelity; dark channel; scale;“halo”artifacts; graying-out 摘 要：针对 MSR 算法在图像去雾应用中存在颜色失真现象且计算量大的问题，提出一种具有颜色保真性的快速 MSR 去雾算法。通过将 MSR 算法对 RGB 三个颜色通道的处理转变为仅对暗原色单一通道进行处理，避免了对颜色通道 间色调相关性的影响，实现颜色保真，同时大大减少了算法执行时间。实验结果表明该算法克服了 MSR 去雾算法 的颜色失真问题，能够有效提升图像的对比度和饱和度，实现图像快速去雾。 关键词：图像去雾；颜色保真性；暗原色通道；尺度；人工“晕化”；灰化 文献标志码：A 中图分类号：TP751 doi：10.3778/j.issn.1002-8331.1410-0045 1 引言 随着全球大气污染问题的恶化，雾霾天气的频繁出 现严重干扰着人们的日常生活。在雾霾条件下拍摄的 户外场景图像由于受到大气散射作用的影响，对比度和 饱和度均产生退化，实用性较差。因此，研究图像去雾 问题，提高雾霾图像的清晰度具有十分重要的意义。 由 Edwin H.Land 和 John J.McCann 于 1970 年提出 的 Retinex 理论 [1]是基于人类颜色知觉的一种图像增强 算法，能对雾霾图像进行有效增强。将 Retinex 理论应 用于图像去雾的研究主要集中在国内。芮义斌、李鹏等 人 采 用 正 态 截 取 的 方 法 对 多 尺 度 Retinex[2]（Multiscale Retinex，MSR）处理后的图像进行拉伸，取得较好的去 薄雾效果 [3]，但该方法未考虑场景中不同区域的雾化程 度。杨万挺、汪荣贵等人根据雾化程度的分布特征设定 滤波尺度参数，提出尺度可变的 Retinex 去雾算法 [4]，对 不同雾化区域进行不同尺度的增强，但区域的划分是根 据区域灰度均值和标准差确定的视觉效果来设定，不够 准确，且计算量较大。 暗原色先验理论是由何凯明提出的一种图像去雾 方法[5]。该理论认为雾霾图像的暗原色值主要由大气散 射光组成，因而可提供对雾分布情况的估计。目前，将 暗原色先验理论与 Retinex 理论相结合进行图像去雾的 研究开始受到关注。汪荣贵、傅剑锋等人在文献[4]的 基础上，根据局部区域暗原色值设定滤波尺度参数[6]，但 雾化程度是凭借经验数据，将暗原色值进行分段来判 定，缺乏理论支撑。舒婷、邓波等人使用暗原色先验方 法进行图像去雾，考虑到增强图像亮度偏暗的问题，再 将增强图像进行 MSR 处理，提高对比度和亮度 [7]，是对 两种理论的组合应用。 以上基于 MSR 的去雾算法分别对 RGB 三个通道进 基金项目：国家自然科学基金（No.11403008）。 作者简介：肖胜笔（1988—），女，硕士研究生，研究领域为图形图像处理、计算机视觉；李燕（1975—），女，博士，副教授，研究领域 为计算机视觉、图形图像处理。E-mail：xiaoshengbi@sina.cn 收稿日期：2014-10-09 修回日期：2014-12-04 文章编号：1002-8331（2015）06-0176-05 CNKI 网络优先出版：2014-12-24，http://www.cnki.net/kcms/detail/11.2127.TP.20141224.1007.008.html 

肖胜笔，李 燕：具有颜色保真性的快速多尺度 Retinex 去雾算法 2015，51（6） 177 3 快速多尺度 Retinex 算法 MSR 算法虽然克服了 SSR 算法的不足，但是，算法 需要分别对 RGB 三个通道进行处理，计算量较大，耗时 多，而且忽视了通道间的色调相关性，产生颜色失真现 象。为了解决这些问题，本文提出了一种具有颜色保真 性的快速 MSR（Fast Multiscale Retinex，FMSR）算法， 以下将从三个方面对算法进行介绍。 3.1 快速策略的提出 在雾霾天气下，大气中漂浮着大量微小水滴、烟、灰 尘等细小颗粒物。这些大气颗粒物通过对光的吸收和 散射作用，直接影响光在大气中的传播，造成光的衰减， 即大气消光。一般情况下，大气消光主要是由散射作用 引起的，通常将这些散射光统称为大气散射光。大气散 射光是造成图像退化最主要的原因，其对光辐射传输的 影响主要表现为：随着距离的增加逐渐地减弱图像的饱 和度，并影响图像的光谱特性，从而造成图像的模糊不 清。由于大气光是由一定频谱范围内的长短波组成，这 些长短波被大气颗粒物同等散射，经混合使得大气散射 光近似于标准白光。因此，可认为雾霾图像质量退化的 一个重要原因是场景中掺入大量白光，造成颜色饱和度 降低。 所以，要增加图像颜色的饱和度，可通过减少图像 中掺入的白光来实现。而在 RGB 颜色空间中，场景中 掺入的白光对各颜色通道的影响是均匀一致的。因此， 考虑直接对图像中的白光分量进行 MSR 处理。这样便 可将原先处理三个通道的计算量转变为仅对白光分量 一个通道进行计算，从而减少算法运行时间。 至此，如何获取雾霾图像中的白光分量便成为 FMSR 算法需要解决的关键问题。 3.2 暗原色通道的引入 通过对大量户外场景无雾图像的观察，在绝大多数 非天空的局部区域内，某些像素点的 RGB 颜色通道中 至少有一个通道值很低，趋近于零。何凯明等人将这个 通道值称为暗原色，并将其定义为[5]： I dark(xy) = min (x′y′)Î Ω(xy) ( min c Î{RGB} I c(x′y′)) （9） 其中 I dark(xy) 表示任意图像 I 的暗原色通道，Ω(xy) 表示以像素点 (xy) 为中心的一个局部区域。并提出暗 原色先验信息的概念——无雾图像 J 中，其暗原色通道 值无限趋近于零，即 J dark(xy)® 0 （10） 为了在 FMSR 算法中引入暗原色通道，可作以下 暗原色先验理论中采用的雾霾图像形成模型为： I(xy) = J (xy)t(xy) + A(1 - t(xy)) （11） 其中 I(xy) 是雾霾图像，J (xy) 是同场景的无雾图像， A 是大气光，t(xy) 是光透射率[5]。 (x,y) = å N w R MSR i (xy) = K n = 1 e-(x2 + y2)/c2 n n n F  F 其中 w 123) 。 n (xy)dxdy = 1 n 是对应尺度的权值，通常取等值 (w = 1/3n = n 推导。 （7） （8） 行处理，不仅计算量大，而且忽视了通道间的色调相关 性，造成颜色失真。尤其在一些颜色单调的区域易产 生灰化现象，失真更严重。为此，人们提出了很多算法 进行颜色恢复 [8-10]。然而，颜色恢复机制虽然解决了灰 化问题，但在色彩较丰富，不产生灰化现象的区域会出 现过恢复的问题，导致更大的颜色失真，增强效果反而 不佳。 本文提出一种新的具有颜色保真性的快速 MSR 去 雾算法。算法通过获取雾霾图像的暗原色通道，将对 RGB 三个通道的处理转变为仅对暗原色通道做处理， 避免了对颜色通道间色调相关性的影响，解决了颜色失 真问题。同时大大减少了算法的执行时间，实现对雾霾 图像快速有效的增强。 2 Retinex 理论基础 Retinex 理论的基本思想是从原图像中获取物体的 反射信息，抛开照度信息，求得物体的本来面貌 [11]。据 此，图像 I(xy) 可表示为： I(xy) = R(xy) × L(xy) （1） 其中 R(xy) 表示反射分量，L(xy) 表示照度分量。通 常将公式两边取对数，以求取反射分量，即 R(xy) = ln I(xy) - ln L(xy) （2） 在 Retinex 理论上发展的单尺度 Retinex（Single Scale Retinex，SSR）算法[12-15]模型为： R i (xy) = ln I i (xy) - ln[F(xy)*I (xy)] i F(xy) = Ke-(x2 + y2)/c2  F(xy)dxdy = 1 （3） （4） （5） (xy) 是原图像在 其中 i Î RGB 表示三个颜色通道，I (xy) 是相应通道的 Retinex 第 i 个颜色通道的分布值，R 输出，F(xy) 是高斯型中心环绕函数，c 是高斯分布的 标准方差，又称尺度，K 是归一化常量。 i i SSR 算法能够取得较好的光照修正或动态范围压 缩特性，但不能同时取得这两个特性，且在边缘处易产 生人工“晕化”现象。为此，Land 等人又提出了 MSR 算 法，表示为[2]： ×{ln I (x,y) - ln[F (x,y)*I i n i (x,y)]}（6） n 综合多尺度优势的 MSR 算法弥补了 SSR 算法的不 足，能同时获得较好的光照修正和动态范围压缩特性， 并消除人工“晕化”现象。 

178 2015，51（6） Computer Engineering and Applications 计算机工程与应用 J c(x′y′))® 0 （13） 得到扩展结果 R '(xy) 。 i FMSR 心环绕函数满足  F 定相应的高斯型中心环绕函数 F n (xy)dxdy = 1 条件的 K 值，从而确 n (xy) 。 n （4）对暗原色通道 I dark 进行 MSR 处理，得到 I dark′ ， 并计算系数矩阵 coef 。 （5）利用系数矩阵 coef 分别扩展 RGB 三个通道， （6）合并扩展后的 RGB 三个颜色通道，得到 FMSR 算法的输出图像。 4 实验结果分析 利用 MSR 算法，MSRCR 算法，文献[7]中算法和本 文提出的 FMSR 算法作对比分析。实验图片取自 NASA 的 Retinex 图像集，实验中所有算法均使用 Intel CoreTM 2 Duo 2.20 GHz CPU，2 GB 内存的 PC 机，在 Windows 7 操作系统下基于 OPENCV/C++编程实现。算法处理结 果对比图如图 1 所示。 ® 现假设每个局部区域内光透射率 t(xy) 为常数，A 值给定，对式（11）两边取两次最小值运算，得到： min (x′y′)Î Ω(xy) ( min c Î{RGB} I c(x′y′)) = J c(x′,y′)) + A(1 - t(x,y))（12） (x′y′)Î Ω(xy) t(x,y) min ( min c Î{RGB} 又由式（9）和（10）可知： J dark(xy) = min (x′y′)Î Ω(xy) ( min c Î{RGB} 则联立式（9）、（12）和（13），可得： I dark(xy) » A(1 - t(xy)) （14） 对 上 式 进 行 分 析 ，因 为 t(xy) 是 光 透 射 率 ，则 A(1 - t(xy)) 表示大气光被大气颗粒物散射后在图像中 的光照信息，即大气散射光。故由上式可推知，暗原色 通道近似等于大气散射光。 因为大气散射光是白光，故可认为，雾霾图像的暗 原色通道实质上表示了图像中掺入的白光分量：暗原色 值越大，掺入的白光分量越多；暗原色值越小，掺入的白 光分量越少。综上所述，FMSR 算法需要的白光分量可 通过计算图像的暗原色通道来获得。 3.3 颜色失真问题的解决 根据人眼结构，所有颜色都可看作是由三个基本颜 色——红（R）、绿（G）和蓝（B）按不同比例组合而成 [16]。 传统的 MSR 算法对 RGB 三个颜色通道分别进行处理， 改变了通道间的比例关系，即 MSR MSR MSR : B : G ¹ R : G : B （15） R 使处理后的图像产生颜色失真。若要保证颜色不 失真，需保证处理后各颜色通道间比例关系保持不变。 由于雾霾图像中掺入的白光分量对三个颜色通道 的影响是均匀一致的，暗原色通道在 MSR 处理前后的 比值与 RGB 各颜色通道增强前后的比值应是相等的关 系。通过计算处理后的暗原色通道值与原值之间的比 值，可得到一个系数矩阵。如果利用该矩阵对 RGB 三 个通道分别进行扩展，可确保图像颜色不会发生失真，从 而解决 MSR 算法的颜色失真问题。 假设对暗原色通道 I dark 进行 MSR 处理后得到 I dark′， 则系数矩阵 coef 的计算表达式为： coef (xy) = I dark′(xy)/I dark(xy) （16） 利用系数矩阵 coef 对 RGB 颜色空间的三个通道分 别进行如下扩展，得到最终的输出图像。 R FMSR '(xy) = I i i (xy)× coef (xy) （17） （a）image 1 （b）image 2 （c）image 3 注：第一行至第五行分别对应原图、MSR 算法、MSRCR FMSR 算法具体步骤总结如下： （1）读入雾霾图像 I(xy) ，分离图像的 RGB 三个颜 算法、文献[7]中算法和 FMSR 算法输出结果图 图 1 算法处理结果对比图 色通道。 （2）求取每个像素点 R、G、B 分量中的最小值，得到 一幅灰度图，对该灰度图进行最小值滤波，得到暗原色 通道 I dark 。 （3）根据设置的低、中、高三个尺度确定使高斯型中 分析四种算法可知，FMSR 算法仅需处理暗原色单 一通道，算法复杂度最低；MSR 和 MSRCR 算法均需处 理 RGB 三个通道，算法复杂度居中，且 MSRCR 算法增 加了颜色恢复，复杂度略高于 MSR 算法；文献[7]中算法 需先利用暗原色先验理论求取无雾图像，再利用 MSR 

肖胜笔，李 燕：具有颜色保真性的快速多尺度 Retinex 去雾算法 2015，51（6） 179 算法进行增强，故算法复杂度最高。统计各算法的执行 时间如表 1 所示。 测试图 image 1 image 2 image 3 MSR 5.813 7.604 7.438 表 1 算法执行时间 MSRCR 文献[7]中算法 6.393 8.309 8.283 7.343 9.608 9.351 s FMSR 3.960 5.221 5.135 从执行时间上看，本文提出的 FMSR 算法比 MSR 和 MSRCR 算法减少约 1/3 的时间，比文献[7]中算法减 少约 1/2 的时间，大大提高了算法的执行效率。 从主观上来看，对比各算法输出结果图，可知 FMSR 算法的视觉效果是最好的，因为其避免了对颜色通道间 色调相关性的影响，具有颜色保真性。而 MSR 和 MSRCR 算法因为忽视了通道间的色调相关性，颜色均有失真，且 MSRCR 由于颜色过恢复的问题，失真更严重。文献[7] 中的算法对增强后的图像再进行 MSR 处理，颜色失真 是最大的。 为了进一步比较各算法性能的优劣，采用图像均 值 [17]、标准差 [17]、信息熵 [17]、对比度 [18]和清晰度 [19]作为客 观评价指标。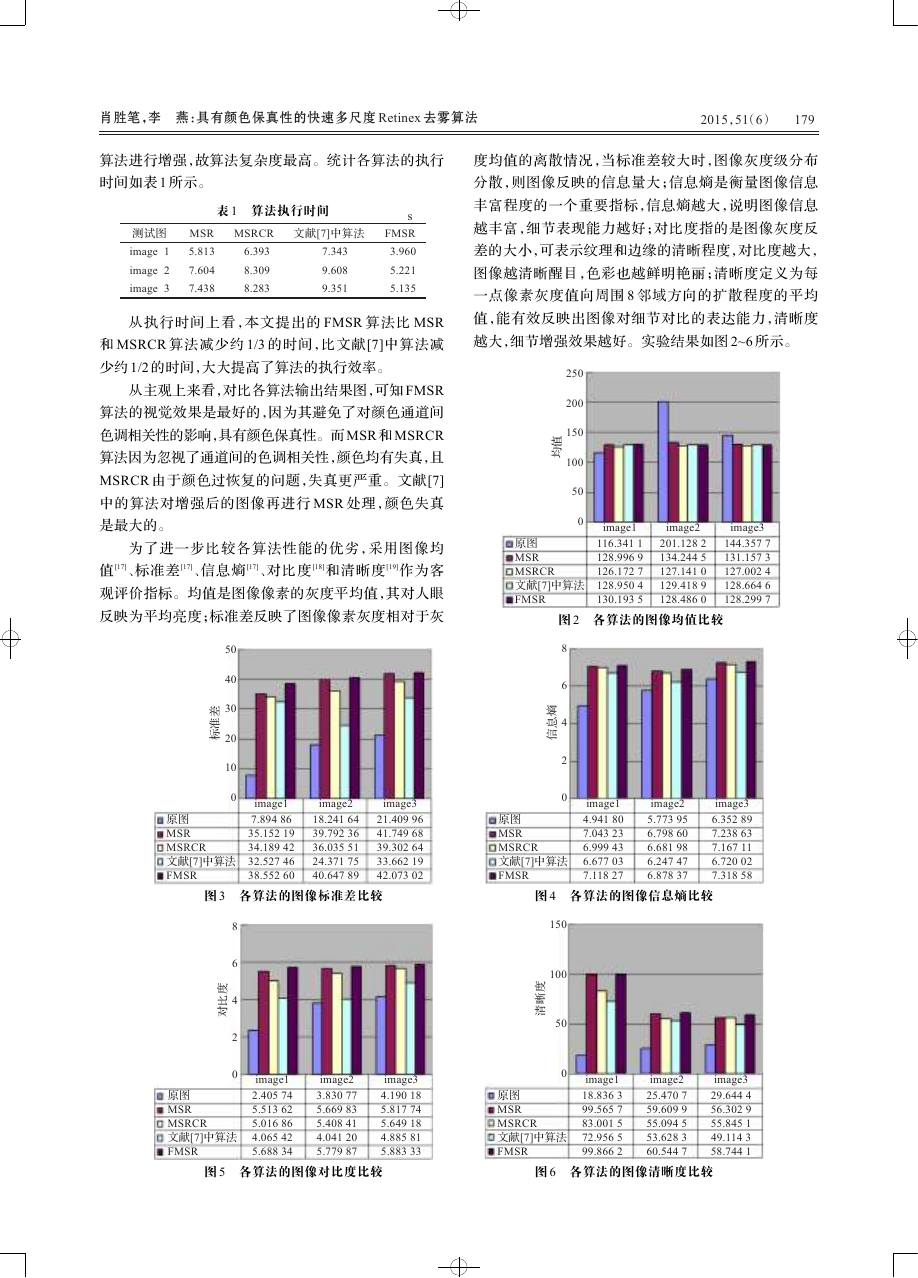均值是图像像素的灰度平均值，其对人眼 反映为平均亮度；标准差反映了图像像素灰度相对于灰 度均值的离散情况，当标准差较大时，图像灰度级分布 分散，则图像反映的信息量大；信息熵是衡量图像信息 丰富程度的一个重要指标，信息熵越大，说明图像信息 越丰富，细节表现能力越好；对比度指的是图像灰度反 差的大小，可表示纹理和边缘的清晰程度，对比度越大， 图像越清晰醒目，色彩也越鲜明艳丽；清晰度定义为每 一点像素灰度值向周围 8 邻域方向的扩散程度的平均 值，能有效反映出图像对细节对比的表达能力，清晰度 越大，细节增强效果越好。实验结果如图 2~6 所示。 250 200 150 100 50 0 值 均 原图 MSR MSRCR 文献[7]中算法 FMSR image1 116.341 1 128.996 9 126.172 7 128.950 4 130.193 5 image2 201.128 2 134.244 5 127.141 0 129.418 9 128.486 0 image3 144.357 7 131.157 3 127.002 4 128.664 6 128.299 7 图 2 各算法的图像均值比较 50 40 30 20 10 0 差 准 标 原图 MSR MSRCR 文献[7]中算法 FMSR image1 7.894 86 35.152 19 34.189 42 32.527 46 38.552 60 image2 18.241 64 39.792 36 36.035 51 24.371 75 40.647 89 image3 21.409 96 41.749 68 39.302 64 33.662 19 42.073 02 8 6 4 2 0 熵 息 信 原图 MSR MSRCR 文献[7]中算法 FMSR image1 4.941 80 7.043 23 6.999 43 6.677 03 7.118 27 image2 5.773 95 6.798 60 6.681 98 6.247 47 6.878 37 image3 6.352 89 7.238 63 7.167 11 6.720 02 7.318 58 图 3 各算法的图像标准差比较 图 4 各算法的图像信息熵比较 8 6 4 2 0 度 比 对 原图 MSR MSRCR 文献[7]中算法 FMSR image1 2.405 74 5.513 62 5.016 86 4.065 42 5.688 34 image2 3.830 77 5.669 83 5.408 41 4.041 20 5.779 87 image3 4.190 18 5.817 74 5.649 18 4.885 81 5.883 33 150 100 50 0 度 晰 清 原图 MSR MSRCR 文献[7]中算法 FMSR image1 18.836 3 99.565 7 83.001 5 72.956 5 99.866 2 image2 25.470 7 59.609 9 55.094 5 53.628 3 60.544 7 image3 29.644 4 56.302 9 55.845 1 49.114 3 58.744 1 图 5 各算法的图像对比度比较 图 6 各算法的图像清晰度比较 

180 2015，51（6） Computer Engineering and Applications 计算机工程与应用 从实验数据分析，各算法增强后的客观性能均优于 原图。从均值性能来看，第一幅图原图偏暗，增强后均 值变大，图像变亮，更清晰。第二幅和第三幅图原图偏 亮，增强后均值下降，图像变暗，更清晰。同时，增强后 图像的标准差、信息熵、对比度和清晰度四项客观指标 均有提高。 由 此 可 知 ，FMSR 算 法 与 传 统 MSR 算 法 相 比 ，在 保 证增强后图像的均值、标准差、信息熵、对比度和清 晰 度 性 能 均 不 变 差 ，甚 至 有 所 改 善 的 情 况 下 ，将 传 统 MSR 算法的执行时间缩短近 1/3，大大提高了算法的执 行效率。 实验结果表明本文提出的 FMSR 算法具有颜色保 真性，能对雾霾图像进行快速去雾，整体视觉效果较好。 5 结束语 本文将暗原色先验理论和 Retinex 理论进行结合， 针对雾霾图像提出了一种具有颜色保真性的快速去雾 算法——FMSR 算法。通过利用雾霾图像的暗原色通 道近似表示图像中掺入的白光分量，将 MSR 算法中对 三个颜色通道的低通滤波转变为仅对暗原色通道作处 理，避免了对通道间色调相关性的影响，具有颜色保真 性。同时减少了算法执行时间，能够对雾霾图像实现快 速有效的增强。 参考文献： [1] Land E H，McCann J J.Lightness and retinex theory[J]. Journal of the Optical Society of America，1971，61（1）： 1-11. [2] Rahman Z，Jobson D J，Woodell G A.Multi-scale retinex for color image enhancement[C]//International Conference on Image Processing，1996：1003-1006. Machine Intelligence，2011，33（12）：2341-2353. [6] 汪荣贵，傅剑锋，杨志学，等.基于暗原色先验模型的 Retinex 算法[J].电子学报，2013，41（6）：1188-1192. [7] 舒婷，邓波，陈炳权，等.基于暗原色先验与 Retinex 理论的去 雾算法[J].吉首大学学报：自然科学版，2014，35（2）：52-56. [8] Rahman Z，Jobson D J，Woodell G A.A multiscale retinex for color rendition and dynamic range compression，NASA Langley Technical Report Server@1996[R].1996. [9] Jobson D J，Rahman Z，Woodell G A.A multiscale retinex for bridging the gap between color images and the human observation of scenes[J].Image Processing，1997，6（7）： 965-976. [10] Hanumantharaju M C，Ravishankar M，Rameshbabu D R， et al.Color image enhancement using multiscale retinex with modified color restoration technique[C]//2011 Second International Conference on Emerging Applications of Information Technology，2011：93-97. [11] Land E H.The retinex theory of color vision[J].Scientific American，1977，237（6）：108-128. [12] Land E H.An alternative technique for the computa- tion of the designator in the retinex theory of color vision[J].Proceedings of the National Academy of Sci- ences，1986，83：3078-3080. [13] Rahman Z.Properties of a center/surround retinex：part 1-signal processing design，NASA Contractor Report# 198194[R].1995. [14] Jobson D J，Woodell G A.Properties of a center/surround retinex：part 2-surround design，NASA Technical Memo- randum#110188[R].1995. [15] Jobson D J，Rahman Z，Woodell G A.Properties and per- formance of a center/surround retinex[J].Image Processing， 1997，6（3）：451-462. [16] 章毓晋.图像处理和分析基础[M].北京：高等教育出版社， [3] 芮义斌，李鹏，孙锦涛.一种图像去薄雾方法[J].计算机应 2007：15-20. 用，2006，26（1）：154-156. [4] 杨万挺，汪荣贵，方帅，等.滤波器可变的 Retinex 雾天图像 增强算法[J].计算机辅助设计与图形学学报，2010，22（6）： 965-971. [5] He Kaiming，Sun Jian，Tang Xiao’ou.Single image haze removal using dark channel prior[J].Pattern Analysis and [17] 赵珍梅，马伟，王润生.三种高保真遥感影像融合方法效 果评价与分析[J].地质与勘探，2010，46（4）：705-710. [18] 陈薇，赵方田，陈侃，等.改进单尺度 Retinex 的光照人脸识 别[J].计算机工程与应用，2013，49（12）：151-154. [19] 赵晓霞，王汝琳.改进的多尺度 Retinex 算法及其应用[J]. 计算机工程，2011，37（6）：209-211.