第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
操作系统计算题总结.docx
西南石油大学软件工程 2008 级 王林
一、第三章的计算有点多（ＰＶ操作，银行家算法，低级
调度算法）
//申请一个资源
//申请失败
ＰＶ操作
操作系统的进程管理中，PV 是重点和难点
信号量：信号量是个数据结构。
struct semaphore{int value;pcb *blockqueue;}mutex;
其中 value 是信号量的值；blockqueue 是等待使用该信号量的进程排成的队列的对手指针。
p 操作：当一个进程对信号量 mutex 执行 p 操作时，执行两个动作：
mutex.valu–；
if (mutex.value<0)
sleep();
v 操作：当一个进程对信号量 mutex 执行 v 操作时，执行两个动作：
mutex.value++；
if (mutex.value>=0)
wakeup();
注：操作系统会保证 PV 操作的原子性，也就是说当一个进程执行 PV 操作，检测信号量时，
不受中断。
看一下 PV 操作实现的功能：
实现进程之间的互斥； 实现进程之间的同步；（接
//从该信号量的等待队列中唤醒一个进程
//本进程进入该信号量等待队列睡眠
//释放一个资源
//如果有进程在等待信号量
下来的两个例题是互斥与同步的典型）
区别：互斥是为了保证资源一次只能由一个进程使用，互斥进程彼此在逻辑上是完全无关的，
它们的运的运行不具有时间次序的特征。而同步是为了实现进程通信，同步进程之间具有合
作关系，在执行时间上须按照一定顺序协同进行。
1.互斥：进出教室问题：有一个变量 count，初值为 0，一个学生进入教室则 count++，出
教室则 count–-。
mutex = 1;
IN:
p(mutex);
count++;
v(mutex);
过程：一个学生进入教室执行 IN，p 操作，mutex.value = 0；假设在进行 count++之前遇到了
中断，而中断之后跳回来时正好这个学生又在出教室，那么这时候就会执行 OUT，mutex.value
= -1，该 OUT 进程进入睡眠，返回 IN 进程，count = 1，v 操作，mutex.value = 0（说明有等
待使用 count 的进程）；唤醒 OUT 进程，count = 0，v 操作，mutex.value = 1。
注意上面划线部分的假设。PV 操作在这就是为了保证这种竞争情况的发生。
OUT:
p(mutex);
count–;
v(mutex);
2.同步：桌上有一空盘，允许存放一只水果。爸爸可向盘中放苹果，也可向盘中放桔子，
西南石油大学软件工程 2008 级 王林
儿子专等吃盘中的桔子，女儿专等吃盘中的苹果。规定当盘空时一次只能放一只水果供吃者
取用，请用 P、V 原语实现爸爸、儿子、女儿三个并发进程的同步。
分析：在本题中，爸爸、儿子、女儿共用一个盘子，盘中一次只能放一个水果。当盘子为空
时，爸爸可将一个水果放入果盘中。若放入果盘中的是桔子，则允许儿子吃，女儿必须等待；
若放入果盘中的是苹果，则允许女儿吃，儿子必须等待。本题实际上是生产者-消费者问题
的一种变形。这里，生产者放入缓冲区的产品有两类，消费者也有两类，每类消费者只消费
其中固定的一类产品。
解：在本题中，应设置三个信号量 S、So、Sa，信号量 S 表示盘子是否为空，其初值为 l；
信号量 So 表示盘中是否有桔子，其初值为 0；信号量 Sa 表示盘中是否有苹果，其初值为 0。
同步描述如下：
int S＝1;int Sa＝0;int So＝0;
main()
{cobegin
father();
son();
daughter();
coend
｝
father()
{while(1)
{P(S);
将水果放入盘中;
if（放入的是桔子）V(So);
else V(Sa);
}
}
son()
{while(1)
{P(So);
从盘中取出桔子;
V(S);
吃桔子;
｝
}
daughter()
{while(1)
{P(Sa);
从盘中取出苹果;
V(S);
吃苹果;
｝
｝
一些问题：为什么要设计三个信号量？因为这里盘子的状态有三种情况。所以在 PV 操作用
在同步的时候，资源都多少种状态，就应该有多少个信号量（高并发的不一定好，需要更多
西南石油大学软件工程 2008 级 王林
的信号量，这样消耗系统的资源就更多）。还有，有没有留意到，每一次“吃”的操作都是
在 V 操作之后进行，这是为什么呢？这是因为 V 操作是释放资源的一个操作，当然是越早
释放对系统越有利啊。
哲学家就餐问题
五个哲学家围坐在一圆桌旁，桌中央有一盘通心粉，每人面前有一只空盘子，每两人之间放
一把叉子；
解一：
设 fork[5]为 5 个信号量，初值为均 1
设信号量 S ，用于封锁第 5 个哲学家，初值为 4。
Philosopheri：
while (1)
{ 思考;
P(S);
P(fork[i]);
P(fork[(i+1) % 5]);
进食;
V(fork[i]);
V(fork[(i+1) % 5]);
V(S);
}
解二：
设 fork[5]为 5 个信号量，初值为均 1。
Philosopher1：
while (1)
{ 思考;
P(fork[1]);
P(fork[2]);
进食;
V(fork[2]);
V(fork[1]);
}
Philosopher2：
while (1)
{ 思考;
P(fork[3]);
P(fork[2]);
进食;
V(fork[2]);
V(fork[3]);
}
西南石油大学软件工程 2008 级 王林
银行家算法
练习：有三类资源 A(17)、B(5)、C(20)。有 5 个进程 P1～P5。T0 时刻系统状态如下：
最大需求
已分配
5
5
5
3
9
6
4
0 11
4
4
2
2
5
4
2
4
4
2
3
1
0
0
0
1
2
2
5
4
4
P1
P2
P3
P4
P5
问(1)T0 时刻是否为安全状态，给出安全系列。
(2)T0 时刻，P2: Request(0,3,4)，能否分配，为什么？
(3)在(2)的基础上 P4:Request(2,0,1)，能否分配，为什么？
(4)在(3)的基础上 P1:Request(0,2,0)，能否分配，为什么？
解析：（1）（求安全系列：说的通俗点就是把所有剩下的资源分给进程，但是要看剩下的资
源数是否能满足进程的需求量，满足了就分给它，等它结束后释放它所拥有的所有资源，再
继续往下分，直到所有的进程都运行成功。）
1>先求剩余量 A(17)、B(5)、C(20) ————三个资源的各自的总量
Work=2 3 3————分给每个进程后三个资源所剩下的量{这样子算的：
A（17）-2-4-4-2-3=2，即总量减去已分配里边竖起来相加的和等于剩余}
2>再求每个进程 T0 时刻的所需量：Need=最大雪球—已分配
综上可得到如图：
最大需求
已分配
P1
P2
P3
P4
5
5
4
4
5
3
9
6
0 11
2
5
2
4
4
2
1
0
0
0
2
2
5
4
Need
3
1
0
2
4
3
0
2
7
4
6
1
西南石油大学软件工程 2008 级 王林
2
4
4
P5
1
观察 Need 的那些值，Work=2 3 3，work 能够 need 的有 P4 跟 P5，二者选哪个都可以，
比如就选择 P4，即我们把 work 的值分给 P4，让它运行完成，P4 释放所有资源，则 work 的
值就变为了 work=4 3 7（P4 的所有资源都要释放哦），再继续找满足条件的进程以此类推，
3
1
4
1
0
可得到安全系列:{P4,P2,P5,P3,P1}(第一问在答题时只需写出一个安全系列就行了，
且安全系列并不确定)
（2）在(2)的基础上 P2: Request(0,3,4)（P2 的 need（=1 3 4））
第一次比较：Request(0,3,4)<= need（=1 3 4）
第二次比较：Request(0,3,4) >=Available (=2 3 3) 因为
Request(0,3,4) >=Available (=2 3 3)
所以不能分配。{ Available (=2 3 3)就是 work =2 3 3，不同的表达而已，但是第二问就是
要这样子写才规范，Request(0,3,4)表示对三种资源的需求，所剩资源必须完全满足需求才可
以分配，否则不行}
（3）P4:Request(2,0,1)
因为 P2 不能分得资源，推迟了，则现在所剩仍是 Available (=2 3 3)，
Request(2,0,1)<=Need（=2 2 1）(第一条件满足了)
Request(2,0,1)<=Available (=2 3 3);（第二条件也满足），接下来还得进行安全性算法检查，先
假定可以分配，若分配后得到我 work（0 3 2），看这时的（0 3 2 ）是否能够让新的形成的
序列达到安全，若是安全就分配，不安全就推迟，经计算是可以形成安全系列{P4，P5，P3，
P2，P1}则可以分配。
（4）在(3)的基础上 P1:Request(0,2,0)
在(3)的基础上，即 P4 运行完成释放了所有资源，这时候 work 的值发生了变化
Work=4 3 7（它是原来的 work 加上已分配得到的），
Request(0,2,0)<= Need（=3 4 7）;
Request(0,2,0) <= Available (=4 3 7),都满足，但是此时的 work 是上次分配后剩下的，即
work（=0 3 2）,若再分配（0 2 0 ）出去，剩下的 work（0 1 2）就不能再满足任何的进程需
要了，所以不可以可以分配。
低级调度算法
低级调度算法老师提到的有三种｛ＦＣＦＳ：先来先服务；ＳＪＦ：短作业优先；ＨＰＦ（Ｈ
ＲＲＮ）：高响应比优先｝（缩写由来 FCFS：First Come First Serve；
SJ(P)F： Shortest Job (Process) First；
（１） 先来先服务：顾名思义，先进来的先运行，运行完了其他后进来的再运行
（２） 短作业优先：进程必须是到达之后，看其还需多少服务时间完成，所有到达的进程
比较，所需服务时间少的先运行，一次类推不断的比较选出可以运行的，直到所有
的都运行完了为止；
HPF：Highest Priority First）
（３） 高响应比优先（就是优先权）：(优先权=等待时间+要求服务时间)/要求服务时间；(或
者优先权=响应时间/要求等待时间)，响应时间=要求等待时间+等待时间；
（４） 周转时间=完成时间-到达时间 带权周转时间=周转时间/服务时间
西南石油大学软件工程 2008 级 王林
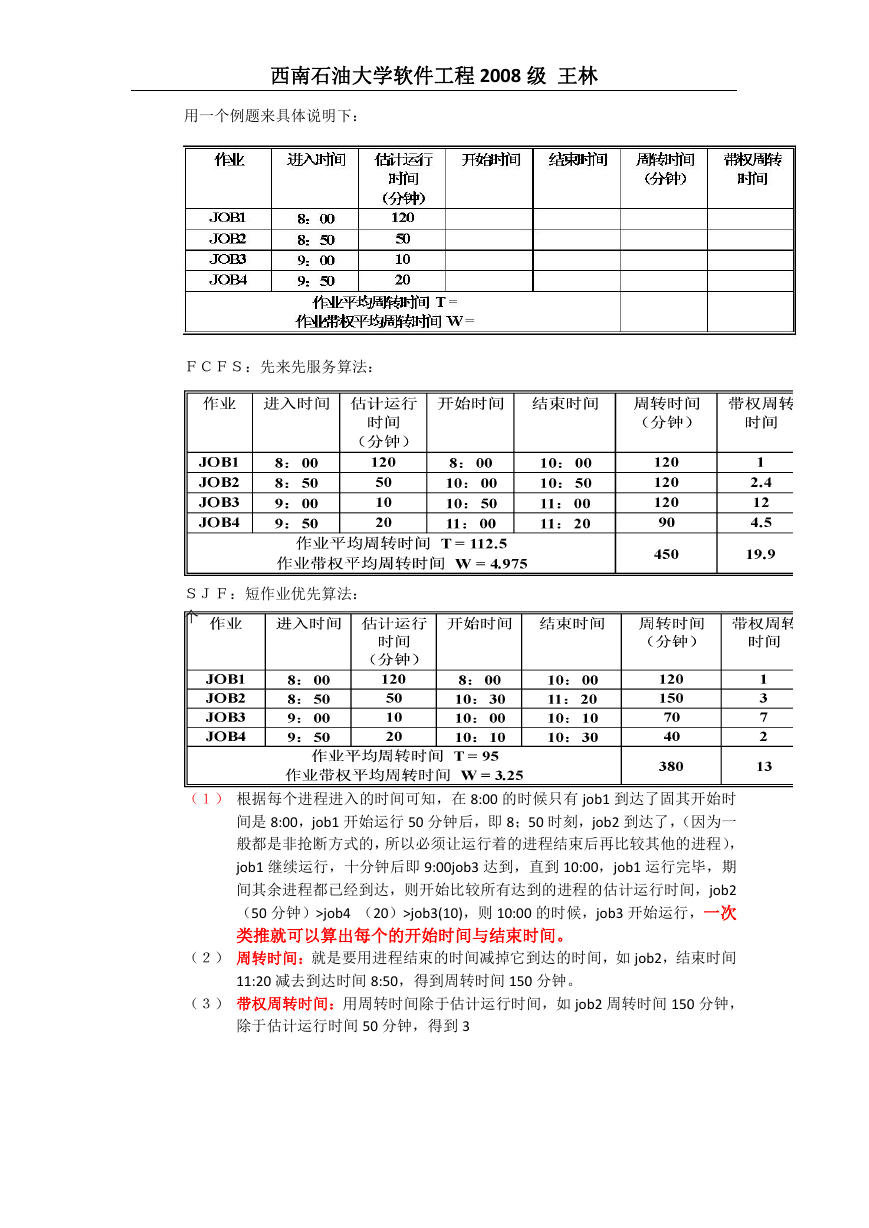
用一个例题来具体说明下：
ＦＣＦＳ：先来先服务算法：
ＳＪＦ：短作业优先算法：
个
（１） 根据每个进程进入的时间可知，在 8:00 的时候只有 job1 到达了固其开始时
间是 8:00，job1 开始运行 50 分钟后，即 8；50 时刻，job2 到达了，（因为一
般都是非抢断方式的，所以必须让运行着的进程结束后再比较其他的进程），
job1 继续运行，十分钟后即 9:00job3 达到，直到 10:00，job1 运行完毕，期
间其余进程都已经到达，则开始比较所有达到的进程的估计运行时间，job2
（50 分钟）>job4 （20）>job3(10)，则 10:00 的时候，job3 开始运行，一次
类推就可以算出每个的开始时间与结束时间。
（２） 周转时间：就是要用进程结束的时间减掉它到达的时间，如 job2，结束时间
11:20 减去到达时间 8:50，得到周转时间 150 分钟。
（３） 带权周转时间：用周转时间除于估计运行时间，如 job2 周转时间 150 分钟，
除于估计运行时间 50 分钟，得到 3
西南石油大学软件工程 2008 级 王林
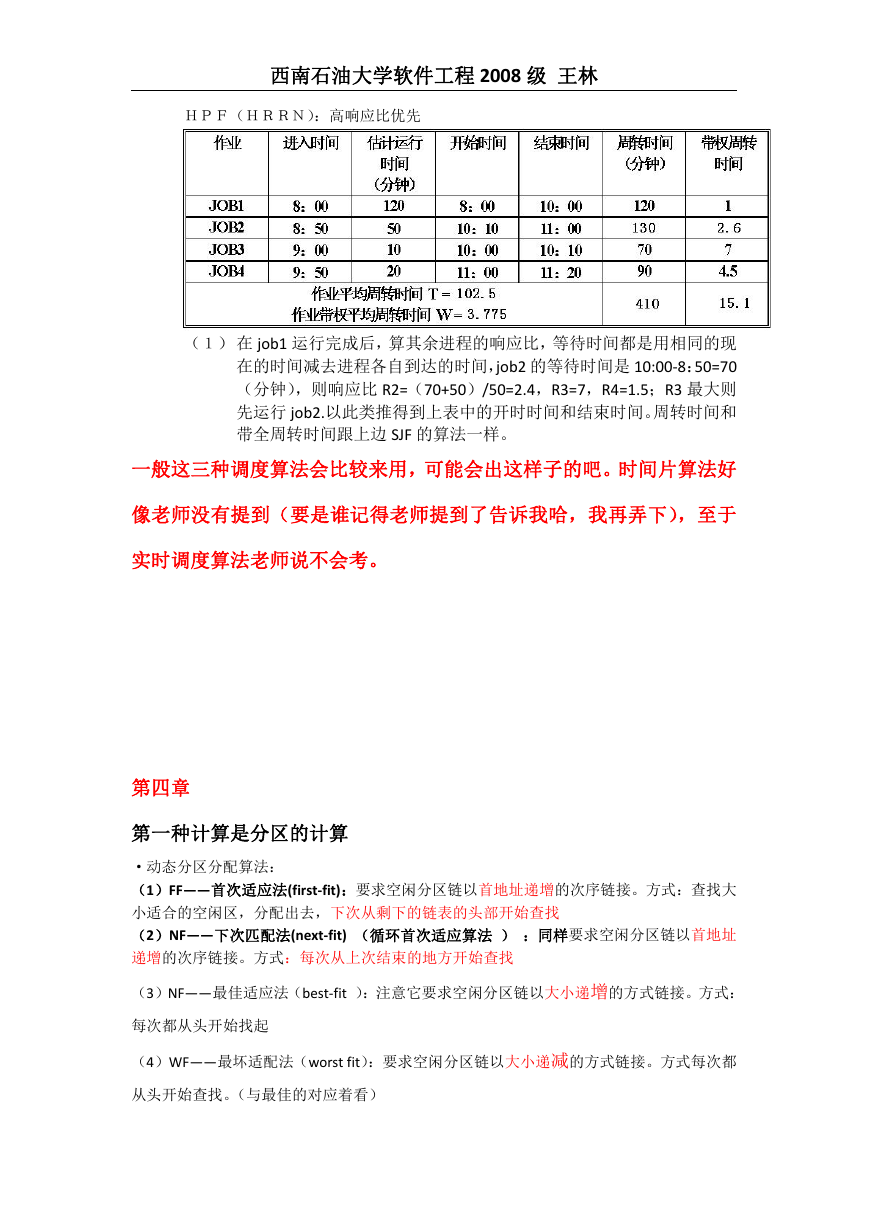
ＨＰＦ（ＨＲＲＮ）：高响应比优先
（１） 在 job1 运行完成后，算其余进程的响应比，等待时间都是用相同的现
在的时间减去进程各自到达的时间，job2 的等待时间是 10:00-8：50=70
（分钟），则响应比 R2=（70+50）/50=2.4，R3=7，R4=1.5；R3 最大则
先运行 job2.以此类推得到上表中的开时时间和结束时间。周转时间和
带全周转时间跟上边 SJF 的算法一样。
一般这三种调度算法会比较来用，可能会出这样子的吧。时间片算法好
像老师没有提到（要是谁记得老师提到了告诉我哈，我再弄下），至于
实时调度算法老师说不会考。
第四章
第一种计算是分区的计算
·动态分区分配算法：
（1）FF——首次适应法(first-fit)：要求空闲分区链以首地址递增的次序链接。方式：查找大
小适合的空闲区，分配出去，下次从剩下的链表的头部开始查找
（2）NF——下次匹配法(next-fit) （循环首次适应算法 ） ：同样要求空闲分区链以首地址
递增的次序链接。方式：每次从上次结束的地方开始查找
（3）NF——最佳适应法（best-fit ）：注意它要求空闲分区链以大小递增的方式链接。方式：
每次都从头开始找起
（4）WF——最坏适配法（worst fit）：要求空闲分区链以大小递减的方式链接。方式每次都
从头开始查找。（与最佳的对应着看）
西南石油大学软件工程 2008 级 王林
（5）BF——快速适应算法（quick fit）：（不好意思，这个只能意会不能言传，别担心，不会
考的）
例题：
有作业序列：作业 A 要求 18K；作业 B 要求 25K，作业 C 要求 30K。系统中空闲区按（首次，
最佳，最坏）三种算法组成的空闲区队列：
上边这三个是链表，只解释首次适应法哈：链表按
首地址 灰色的区域为空闲容量
首地址递增的方式排列，即 20,100,160,210.（30,20,5,4 这几个数是空闲区的大小），接下来
就用那三个作业的大小与空闲区比较，A 作业要求 18K，首地址是 20 的空闲区有 30K 的容
量，它满足条件，则把她分配给作业 A，再找作业 B 的 25K，没有能满足条件的，查找失败。
其他两个队列也这么用，然后比较三种算法，哪种比较适合这个作业序列：
经分析可知：最佳适应法对这个作业序列是合适的，而其它两种对该作业序列是不
合适的。
再赠送道练习题：
有作业序列：作业 A 要求 21K；作业 B 要求 30K，作业 C 要求 25K。
算法有多种，虽然比较的时候一般是两三种，但是这两三种都不一定适合当时的作业序列哈。
第二种计算是页面置换的计算
有两类，第一类：逻辑地址到物理地址的转换
页号和页内地址的计算
若给定一个逻辑地址空间中的地址为 A，页面大小为 L，则页号 P 和页内地址 d 可按下式求
得：
P = A div L
d = A mod L
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
