logo资料库

2020深圳杯C题.docx

发布时间：2022-06-15 发布人：admin 分类：说明书 资料大小：0.34M 资料格式：docx 举报 版权申诉
第1页 / 共19页
第2页 / 共19页
第3页 / 共19页
第4页 / 共19页
第5页 / 共19页
第6页 / 共19页
第7页 / 共19页
第8页 / 共19页
资料共19页，剩余部分请下载后查看
    C题：无线可充电传感器网络充电路线规划
    摘要
    1.问题重述
    2.问题分析与思考
    2.1问题一分析 ：
    2.2 问题二分析：
    2.3 问题三分析：
    3. 模型假设
    4.符号说明
    5.模型建立
    5.1问题一模型建立与求解
    5.2问题二模型建立与求解
    电池容量推导：
    数值解结果
    5.3问题三模型建立与求解
    6.模型评价
    6.1模型优点
    6.2模型缺点
    附录
    C 题：无线可充电传感器网络充电路线规划 摘要 物联网的快速发展带动了无线传感器网络 WSN 在生活中的广泛运用。无线传 感器网络中包括若干传感器以及一个数据中心，这些传感器的电池均需要移动充 电器提供能量来维持正常的工作。移动充电器的能量一方面用于传感器的充电， 另一方面用于充电路上的消耗。为减少移动充电器路上消耗，提高能量利用率， 需要合理规划移动充电器充电路线。 针对问题一，要使得能耗最小化，就要保证移动充电器行走的路程最小，所 以路线图可看成网络图，利用地球半径和各传感器的经纬度计算可以得出各个点 之间的距离，问题转化为在给定的加权网络图中寻找从数据中心开始将网络图中 所有顶点仅遍历一遍再回到数据中心使得路程最短的问题，即 TSP 问题，运用 python 的 OR-TOOLS 的 RoutingModel，结合启发式算法，可得到最优路线方案。 针对问题二，系统正常运行需要保证移动充电器跑完一圈的过程后各传感器 一直不低于最低电池容量，可以将此作为约束条件，若要求得每一个满足题设条 件传感器的电池容量最小值，可以等价为求传感器总电池容量的最小值，这样就 将多目标问题转化为了单目标问题，经简化计算进一步转化为线性规划问题，合 理设置充电速率 r，移动速度 v，电池容量最低值 f,通过求解我们得到各传感器 的最小电池容量；在此基础上我们考虑到巡视间隔为 1 天，保证相邻两次巡视之 间传感器的电池电量仍然满足要求，得到电池容量。 针对问题三，规划同时派出 4 个移动充电器进行充电的路线可以联系多售货 员的旅行商问题，即 VRP 问题，当 VRP 问题有到达时间的约束条件时，问题变为 VRPTW 问题（VRP with Time Windows），基于第一问的我们得到最优的路线方 案，结合第二问进一步得到各电池最低容量。 关键词： OR-TOOLS TSP 问题 启发式算法 VRPTW 问题 1.问题重述 随着物联网的快速发展，无线传感器网络 WSN 在生活中的应用也越来越广 泛。无线传感器网络中包括若干传感器以及一个数据中心。传感器从环境中收集 信息后每隔一段时间将收集到的信息发送到数据中心。数据中心对数据进行分析 并回传控制信息。影响生命周期最重要的一个因素是能量。提供能量的方式之一 是电池供电，利用移动充电器定期为传感器的电池补充能量，这种方式供电的网 络也被称为无线可充电传感器网络。 在系统中，传感器从环境中收集信息并将收集到的信息传递给数据中心。当 一个传感器的电量低于一个阈值时便无法进行正常的信息采集工作，为了让 WRSN 正常运转，移动充电器需要定期为传感器进行充电以避免其电量低于阈值。 为了减小移动充电器在路上的能量消耗，需要合理地规划移动充电器的充电路 线。请考虑以下问题：
    问题一：根据每个节点的经纬度，考虑当只派出一个移动充电器时，如何规划移 动充电路线才能最小化移动充电器在路上的能量消耗。 问题二：知道每个节点的经纬度、能量消耗速率，假设传感器的电量只有在高于 时才能正常工作，移动充电器的移动速度为 v(m/s)、移动充电器的充电速率为， 在只派出一个移动充电器的情况下，若采用问题一规划出来的充电路线，每个传 感器的电池的容量应至少是多大才能保证整个系统一直正常运行？ 问题三：知道每个节点的经纬度、能量消耗速率，假设传感器的电量只有在高于 时才能正常工作，移动充电器的移动速度为 v(m/s)、移动充电器的充电速率为， 但为了提高充电效率，同时派出 4 个移动充电器进行充电，在这种情况下应该如 何规划移动充电器的充电路线以最小化所有移动充电器在路上的总的能量消 耗？每个传感器的电池的容量应至少是多大才能保证整个系统一直正常运行？ 2.问题分析与思考 2.1 问题一分析 ： 问题一属于典型的旅行商问题，该问题是在寻求一个充电器由起点出发，通 过所有给定的传感器位置点之后，最后再回到原点的最小路径。问题的求解有多 种方式，我们在这里采用 python 的 OR-TOOLS 的 RoutingModel 来求解此问题。 附件一给出了 29 个传感器以及数据中心的经纬度，先将经纬度转换为弧度，再 利用地球半径计算可以得出各个点之间的距离，从而可以求得这些点的距离矩 阵，运用启发式算法，根据以上两种不同的求解方式会得出不同的最短路径（即 最优路径），再对结果进行分析比较，得到最佳路线规划方案。 2.2 问题二分析： 若将每一个传感器的电池容量都视作一个目标，则此问题属于多目标优化问 题，在此题中，若要求得每一个满足题设条件传感器的电池容量最小值，可以等 价为求传感器总电池容量的最小值，这样就将多目标问题转化为了单目标问题， 根据题意，我们可以合理假设移动充电器的巡逻速率和频率，从而得到约束条件： 在移动充电器巡逻一个周期（即绕所有点走一圈）内，每个传感器的电池容量最 低不能低于,利用这一条件，我们可以建立不等式约束，从而进一步将问题转化 为线性规划问题，利用线性规划的求解方式解得每一传感器满足题设条件的电池 容量最小值。 2.3 问题三分析： 由于有多辆车进行运送，要是以最小化路径为目标函数，可能会造成某辆车 的运送时间过长而导致总时间并不是最短的。所以目标函数应为：若设车队的运 送时间为$T = {t_1,t_2,t_3,t_4}$，车队的运输路径长度$L = {l_1, l_2, l_3, l_4}$。则最小化$T$中最大的值，也可以解释为最小化$T$中的最大值。综上所
    述，该问为有时间窗车辆路径问题（vehicle routing problems with time windows），题目要求同时派出 4 个移动充电器进行充电，在这种情况下规划移 动充电器的充电路线，使得移动充电器在路上总的能量消耗最小。因此首先考虑 运用 python 的 OR-TOOLS，然后进一步分组利用启发式算法求得最短巡视路径， 在第二问的解法基础上计算传感器满足题设条件的电池容量最小值。 3. 模型假设 3.1 假设移动充电器匀速行进； 3.2 假设题目所给数据真实可靠； 3.4 假设地球是一个标准的球体，半径是 6371km； 3.5 假设移动充电器在传感器处的时间消耗仅用于充电； 3.6 假设移动充电器的电池电量足够大，且不需要在数据中心进行充电。 xi ttot ri f v St 4. 符号说明 电池容量 mA 到达该节点时，剩余电池容量刚好为最 低要求时间 t 移动充电器充电速率 mA/s 电容器最低工作值 mA 充电器移动速率 m/s 移动充电器到传感器的距离 m 5.模型建立 5.1 问题一模型建立与求解 1.计算欧几里得距离矩阵 给数据中心编号为 0，传感器依次编号为 1，2,3…29，最后数据中心再重复 编号为 30。建立距离矩阵，distances 表示两点间的距离。则问题是由 0 出发， 走过中间所有的点，到达 0 的一个最短路径。解空间是所有固定起点与终点的循 环排列组合。运用 Python 的 geopy 库换算经纬度，求距离矩阵。 2.运用 python 的 OR-TOOLS 的 RoutingModel 解决 TSP 问题 3.首先建立 RoutingModel 模型，SetArcCostEvaluatorOfALLVehi 4.cles 方法传入一个计算距离的回调函数，设定初始可行解的求解方案为 first_solution_strategy（选项为 PATH_CHEAPEST_ARC）和
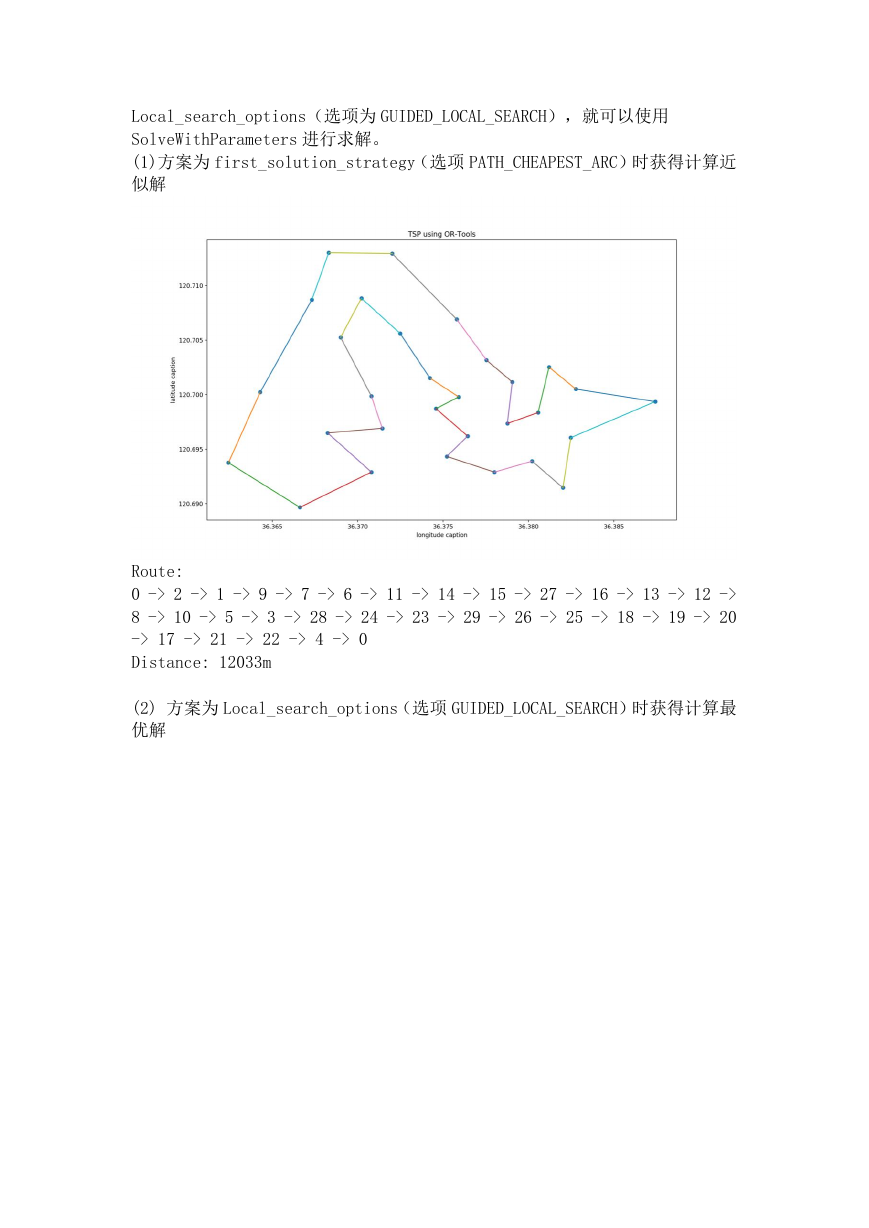
    Local_search_options（选项为 GUIDED_LOCAL_SEARCH），就可以使用 SolveWithParameters 进行求解。 (1)方案为 first_solution_strategy（选项 PATH_CHEAPEST_ARC）时获得计算近 似解 Route: 0 -> 2 -> 1 -> 9 -> 7 -> 6 -> 11 -> 14 -> 15 -> 27 -> 16 -> 13 -> 12 -> 8 -> 10 -> 5 -> 3 -> 28 -> 24 -> 23 -> 29 -> 26 -> 25 -> 18 -> 19 -> 20 -> 17 -> 21 -> 22 -> 4 -> 0 Distance: 12033m (2) 方案为 Local_search_options（选项 GUIDED_LOCAL_SEARCH）时获得计算最 优解
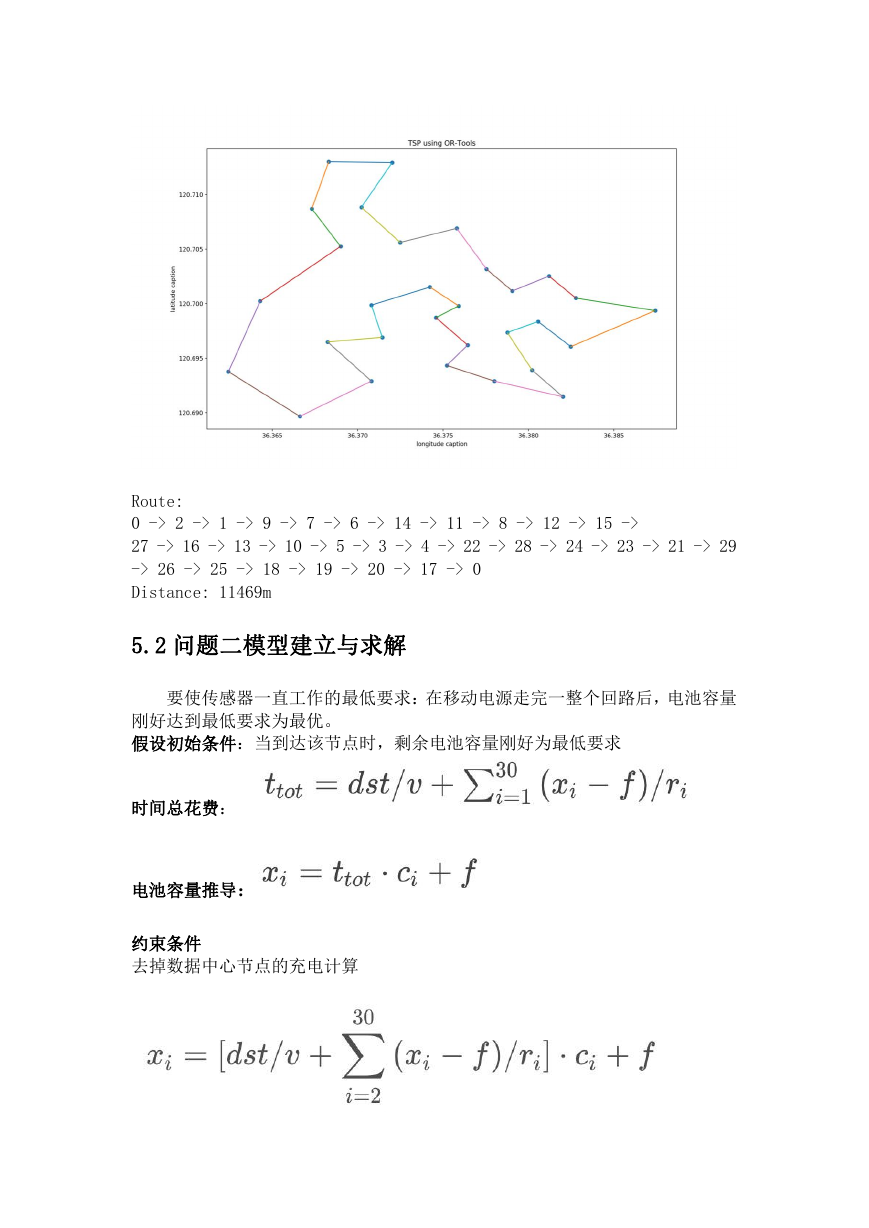
    Route: 0 -> 2 -> 1 -> 9 -> 7 -> 6 -> 14 -> 11 -> 8 -> 12 -> 15 -> 27 -> 16 -> 13 -> 10 -> 5 -> 3 -> 4 -> 22 -> 28 -> 24 -> 23 -> 21 -> 29 -> 26 -> 25 -> 18 -> 19 -> 20 -> 17 -> 0 Distance: 11469m 5.2 问题二模型建立与求解 要使传感器一直工作的最低要求：在移动电源走完一整个回路后，电池容量 刚好达到最低要求为最优。 假设初始条件：当到达该节点时，剩余电池容量刚好为最低要求 时间总花费： 电池容量推导： 约束条件 去掉数据中心节点的充电计算
    根据约束条件得出线性方程组 组合结果为一个 29*29 的矩阵： 数值解结果 传感器最低电池容量 f/mA 电容器 5145.627704 5692.659704 4940.490704 5168.420704 4735.353704 4940.490704 5373.557704 4963.283704 4940.490704 5168.420704 4940.490704 5601.487704 5396.350704 4940.490704 4780.939704 4940.490704 5168.420704 5624.280704 5168.420704 4940.490704 4712.560704 5168.420704 5624.280704 4712.560704 5168.420704 4894.904704 X1 X2 X3 X4 X5 X6 X7 x8 X9 x10 X11 x12 x13 x14 X15 X16 X17 X18 X19 X20 X21 X22 X23 X24 X25 X26
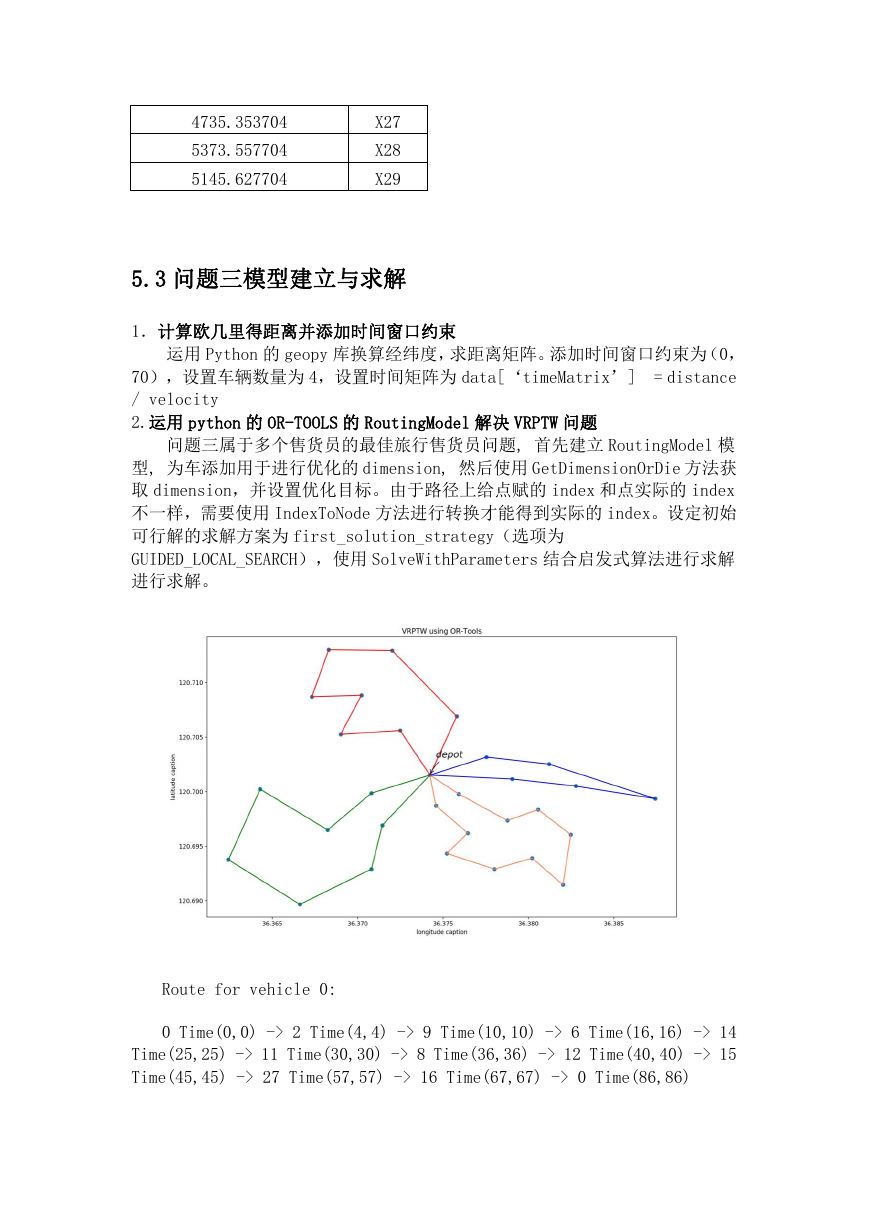
    4735.353704 5373.557704 5145.627704 X27 X28 X29 5.3 问题三模型建立与求解 1．计算欧几里得距离并添加时间窗口约束 运用 Python 的 geopy 库换算经纬度，求距离矩阵。添加时间窗口约束为（0， 70），设置车辆数量为 4，设置时间矩阵为 data[‘timeMatrix’] / velocity 2.运用 python 的 OR-TOOLS 的 RoutingModel 解决 VRPTW 问题 = distance 问题三属于多个售货员的最佳旅行售货员问题, 首先建立 RoutingModel 模 型, 为车添加用于进行优化的 dimension, 然后使用 GetDimensionOrDie 方法获 取 dimension，并设置优化目标。由于路径上给点赋的 index 和点实际的 index 不一样，需要使用 IndexToNode 方法进行转换才能得到实际的 index。设定初始 可行解的求解方案为 first_solution_strategy（选项为 GUIDED_LOCAL_SEARCH），使用 SolveWithParameters 结合启发式算法进行求解 进行求解。 Route for vehicle 0: 0 Time(0,0) -> 2 Time(4,4) -> 9 Time(10,10) -> 6 Time(16,16) -> 14 Time(25,25) -> 11 Time(30,30) -> 8 Time(36,36) -> 12 Time(40,40) -> 15 Time(45,45) -> 27 Time(57,57) -> 16 Time(67,67) -> 0 Time(86,86)
    Time of the route: 86 seconds Route for vehicle 1: 0 Time(0,0) -> 1 Time(5,5) -> 7 Time(12,12) -> 20 Time(21,21) -> 19 Time(28,28) -> 18 Time(36,36) -> 25 Time(46,46) -> 26 Time(57,57) -> 29 Time(69,69) -> 0 Time(91,91) Time of the route: 91 seconds Route for vehicle 2: 0 Time(0,0) -> 5 Time(7,7) -> 10 Time(11,11) -> 13 Time(16,16) -> 3 Time(30,30) -> 0 Time(40,40) Time of the route: 40 seconds Route for vehicle 3: 0 Time(0,0) -> 17 Time(8,8) -> 21 Time(18,18) -> 23 Time(25,25) -> 24 Time(33,33) -> 28 Time(41,41) -> 22 Time(49,49) -> 4 Time(56,56) -> 0 Time(64,64) Time of the route: 64 seconds Total time of all routes: 281min 6.模型评价 6.1 模型优点 1. 本文采用的启发式算法计算精度高、运算时间短。 2. 本文建立的模型能结合实际情况对问题进行求解，实用性强。
    分享到：
    赞 收藏

    相关推荐

    资料库

    后端

    共收录2142份资料，累计10个分类，关注成员有19位，主要包括：Perl,Docker,Delphi,VB,PHP,Java,C,C#,Python,C++

    热门标签

    Perl Docker Delphi VB PHP Java C C# Python C++

    最新资料