面试手撕代码整理.pdf-资料库

//求一个数的平方根 int sqrt(int x) { if (x <= 0) return 0; double c = x; double old; do { old = c; c = (c + x / c) / 2.0; } while (fabs(old - c) > 0.000001); return int(c); } //二叉树深度计算 class BinaryTree { public: BinaryTree *lChild, *rChild; int value; }; //递归 int computeTreeDepth(BinaryTree* binaryTree) { if (binaryTree == nullptr) { return 0; } if (binaryTree->lChild == nullptr && binaryTree->rChild == nullptr) { return 1; } int lDepth = computeTreeDepth(binaryTree->lChild) + 1; int rDepth = computeTreeDepth(binaryTree->rChild) + 1; return max(lDepth, rDepth); } //非递归 int computeTreeDepth(BinaryTree *binaryTree) { //实例化队列 queue mVisitList; BinaryTree *tmp; int depth = 0; if (binaryTree == nullptr) { //根为空，直接返回0 return 0; } //将根加入队列 mVisitList.push(binaryTree); while (!mVisitList.empty()) {

//只要队列不为空，说明新的一层数据不为空，且已经加到队列，深度+1 depth++; //遍历该层到所有数据，将他们出队，并附带把所有下一层到数据都加进来(如果有的话) int lengthTmp = mVisitList.size(); while (lengthTmp--) { tmp = mVisitList.back(); mVisitList.pop(); if (tmp->lChild != nullptr) { mVisitList.push(tmp->lChild); } if (tmp->rChild != nullptr) { mVisitList.push(tmp->rChild); } } } return depth; } //在二叉树中找到两个节点的最近公共祖先 class BinaryTree { public: BinaryTree(int value) :value(value) {} int value; BinaryTree *LeftTree; BinaryTree *RightTree; }; bool FindPath(BinaryTree *pHead, BinaryTree *pNode, vector& path) { } if (pHead == nullptr) return false; path.push_back(pHead); if (pHead == pNode) return true; if (FindPath(pHead->LeftTree, pNode, path)) return true; if (FindPath(pHead->RightTree, pNode, path)) return true; path.pop_back(); return false; BinaryTree* TheCommomNode(BinaryTree*pHead, BinaryTree*pNode1, BinaryTree*pNode2) { if (pHead == nullptr) return nullptr;

vectorpath1; vectorpath2; FindPath(pHead, pNode1, path1); FindPath(pHead, pNode2, path2); int s1 = path1.size(); int s2 = path2.size(); if (s1 > s2) { } int tmp = s1 - s2; while(tmp--) { } path1.pop_back(); if (s1 < s2) { } int tmp = s2 - s1; while (tmp--) { } path2.pop_back(); while (1) { } if (path1.back() == path2.back()) return path1.back(); path1.pop_back(); path2.pop_back(); } //快速排序 void QuickSort(int *a, int start, int end) { if (start >= end) return; int pivot = a[start]; int left = start; int right = end;

while (left != right) { } while (a[right] > pivot && left < right) right--; while (a[left] <= pivot && left < right) left++; if (left < right) { } int p = a[right]; a[right] = a[left]; a[left] = p; a[start] = a[left]; a[left] = pivot; QuickSort(a, start, left - 1); QuickSort(a, left + 1, end); } //冒泡排序 void BubbleSort(int *L, int len) { } for (int i = 0; i < len - 1; i++) { } for (int j = len - 2; j >= i; j--) { } if (L[j] > L[j + 1]) swap(L, j, j + 1); //归并排序 void Merge(int SR[], int TR[], int l, int m, int r) { int i, j, p; for (i = l, j = m + 1; l <= m&&j <= r; i++) { if (SR[l] < SR[j]) TR[i] = SR[l++]; else

TR[i] = SR[j++]; } if (l <= m) { } for (p=0;p<=m-1;p++) TR[i + p] = SR[l + p]; if (j <= r) { } for (p = 0; p <= r - j; p++) TR[i + p] = SR[j + p]; } void MSort(int SR[], int TR1[], int s, int t) { int TR2[MAX + 1]; int m; if (s == t) TR1[s] = SR[s]; else { m = (s + t) / 2; MSort(SR, TR2, s, m); MSort(SR, TR2, m+1, t); Merge(TR2, TR1, s, m, t); } } //选择排序 void SelectSort(int a[], int len) { } int min; for (int i = 0; i < len - 1; i++) { } min = i; for (int j = i+1; j < len ; j++) { } if (a[min]>a[j]) min = j; if (i!=min) swap(a, i, min);

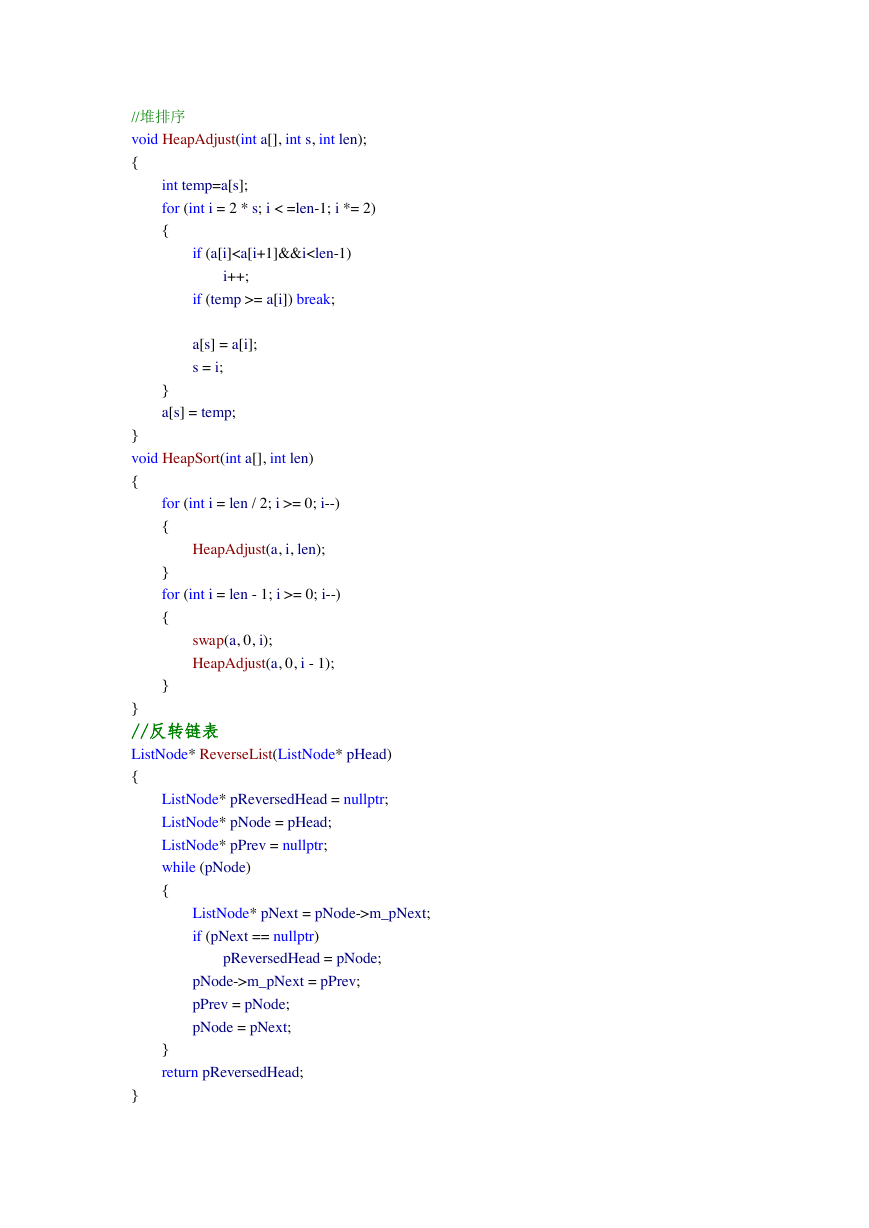
//堆排序 void HeapAdjust(int a[], int s, int len); { } int temp=a[s]; for (int i = 2 * s; i < =len-1; i *= 2) { } if (a[i]= a[i]) break; a[s] = a[i]; s = i; a[s] = temp; void HeapSort(int a[], int len) { for (int i = len / 2; i >= 0; i--) { } HeapAdjust(a, i, len); for (int i = len - 1; i >= 0; i--) { } swap(a, 0, i); HeapAdjust(a, 0, i - 1); } //反转链表 ListNode* ReverseList(ListNode* pHead) { } ListNode* pReversedHead = nullptr; ListNode* pNode = pHead; ListNode* pPrev = nullptr; while (pNode) { } ListNode* pNext = pNode->m_pNext; if (pNext == nullptr) pReversedHead = pNode; pNode->m_pNext = pPrev; pPrev = pNode; pNode = pNext; return pReversedHead;

//删除链表中的节点 void DeleteNode(ListNode** pListHead, ListNode *pToBeDeleted) { } if (pListHead == nullptr || pToBeDeleted == nullptr) return; if (pToBeDeleted->m_pNext != nullptr) //要删除的节点不是尾节点 { ListNode *pNext = pToBeDeleted->m_pNext; pToBeDeleted->m_nValue = pNext->m_nValue; pToBeDeleted->m_pNext = pNext->m_pNext; delete pNext; pNext = nullptr; } else if (*pListHead == pToBeDeleted) //链表只有一个节点，删除头结点 { delete pToBeDeleted; pToBeDeleted = nullptr; pListHead = nullptr; } else //要删除的结点是尾节点 { } ListNode *pNode = *pListHead; while (pNode->m_pNext != pToBeDeleted) pNode = pNode->m_pNext; pNode->m_pNext = nullptr; delete pToBeDeleted; pToBeDeleted = nullptr; //面试题39：数组中出现次数超过一半的数字 int MoreThanHalfNum_Solution(vector numbers) { int result = numbers[0]; int times = 1; for (int i = 1; i < numbers.size(); i++) { if (result == numbers[i]) times++; else times--; if (times == 0) { result = numbers[i]; times = 1;

} } int count = 0; // 出现次数 for (int i = 0; i < numbers.size(); ++i) { } if (numbers[i] == result) ++count; return (count > numbers.size() / 2) ? result : 0; } //辗转相除法 int maxCommonValue(int a, int b) { int big = a > b ? a : b; int small = a < b ? a : b; if (big%small == 0) return small; return maxCommonValue(big%small, small); } //更相减损术 int maxCommonValue(int a, int b) { } if (a == b) return a; int big = a > b ? a : b; int small = a < b ? a : b; return maxCommonValue(big-small, small); //删除链表中重复的节点 void DeleteDuplication(ListNode** pListHead) { if (pListHead == nullptr) return; ListNode*pPreNode = nullptr; ListNode*pNode = *pListHead; while (pNode != nullptr) { ListNode*pNext = pNode->m_pNext; bool iDelete = false; if (pNext != nullptr&&pNext->m_nValue == pNode->m_nValue)

资料库

面试手撕代码整理.pdf

相关推荐

课程资源

热门标签

最新资料