quaternion.pdf-资料库

1514951f-7235-4980-bbd4-c089c1accc4b.pdf-第1页.png

第1页 / 共72页

1514951f-7235-4980-bbd4-c089c1accc4b.pdf-第2页.png

第2页 / 共72页

1514951f-7235-4980-bbd4-c089c1accc4b.pdf-第3页.png

第3页 / 共72页

1514951f-7235-4980-bbd4-c089c1accc4b.pdf-第4页.png

第4页 / 共72页

1514951f-7235-4980-bbd4-c089c1accc4b.pdf-第5页.png

第5页 / 共72页

1514951f-7235-4980-bbd4-c089c1accc4b.pdf-第6页.png

第6页 / 共72页

1514951f-7235-4980-bbd4-c089c1accc4b.pdf-第7页.png

第7页 / 共72页

1514951f-7235-4980-bbd4-c089c1accc4b.pdf-第8页.png

第8页 / 共72页

四元数与三维旋转 Krasjet 这篇文章的主要目的就是简单讨论一下四元数（Quaternion）与三维旋转之间的关系．虽然网上四元数相关的资料有很多了，但是我好像一直没找到令我满意的，所以就想自己来写一篇．目前很多资料都使用了比较抽象的方式来解释这一主题，而且在某一些点上讲得不是很清楚．因为 3D空间还是在我们理解范围之内的，所以四元数与三维旋转的一些关系可以直接使用一些基础的几何学和线性代数的知识来推导和理解，并不会那么复杂．我们在大部分的时间中也会采用这一方式来理解四元数，如果你对更抽象的内容感兴趣，我在最后也非常浅显地提到一些，但是它们不是我们的重点．因为我们主要的侧重点会偏向几何以及计算机图形学中的应用，如果你是因为在学习物理学或者抽象代数来看这篇文章，我不确定这篇文章能否帮助到你．当然，我在最后提到的一些拓展阅读可能还是有一点用的．我在写这篇文章的时候顺手写了一些用于 Demo的 MATLAB/Octave代码，并且将动画导出为了 GIF，你可以在 GitHub上找到它们：https://github.com/Krasjet/quaternion 因为写完之后仅仅只校对过一遍_(:з」∠)_，所以肯定会存在很多错误．如果你发现有任何错误或者对内容有什么意见，请直接到 GitHub的 Issues里报告．本文采用「CC BY-NC-SA 4.0」协议，在共享的时候请记得署名以及采用相同的协议，并且不要用于商业用途． 1 复数在介绍四元数与 3D 旋转之间的关系之前，我们先来讨论一下复数（Complex Number）的一些性质以及它与 2D旋转之间的关系．四元数的很多性质在很多层面上都与复数非常类似，所以理解复数的一些性质会对理解四元数非常有帮助．因为复数不是我们的重点，下面对复数的讨论不会非常全面．如果你对复数已经非常了解了，也可以直接跳到第二章． 1

1.1 定义任意一个复数 z ∈ C都可以表示为 z = a + bi的形式，其中 a, b ∈ R而且 i2 = −1．我们将 a 称之为这个复数的实部（Real Part），b 称之为这个复数的虚部（Imaginary Part）．因为 z = a + bi其实就是对于 {1, i}这个基（Basis）的线性组合（Linear Combination），我们也可以用向量来表示一个复数： 24a 35 z = b 因为这个向量有两个元素，我们可以使用复平面上的一个点来表示一个复数．复平面的横坐标 Re代表它的实部，纵坐标 Im代表它的虚部： Im bi z = a + bi Re a 1.2 性质 1.2.1 复数加减法如果我们有两个复数 z1 = a + bi, z2 = c + di，它们的和就是分量相加的结果： z1 + z2 = (a + c) + (b + d)i 同理，如果要对它们相减，直接将分量相减就可以了： z1 − z2 = (a − c) + (b − d)i 虽然复数的加减法还有很多其它的性质，但是加减法并不是我们的重点，我们需要关注的是复数的乘法． 2

1.2.2 复数乘法如果有两个复数 z1 = a + bi, z2 = c + di，我们可以使用分配律来计算它们的乘积： z1z2 = (a + bi)(c + di) = ac + adi + bci + bdi2 因为 i2 = −1，这可以进一步化简为 z1z2 = ac − bd + adi + bci = ac − bd+ (bc + ad)i 如果仔细观察你就能发现，复数相乘的结果其实也是一个矩阵与向量相乘的结果，也就是说： z1z2 = ac − bd+ (bc + ad)i 24a −b 35 3524c 35是用向量的形式来表示的 z2，而左侧的 24a −b = b a d d 24c 24a −b 35则是 z1 的矩阵形式． 35这个矩阵所代表的变换是等右侧的我们可以发现，复数相乘这个运算，其实是与价的（虽然复数与这个矩阵的关系远远不止这些，但是你只需要理解它所代表的变换与复数的乘法运算之间的关系就可以了）．那么，在矩阵形式下，复数与复数的相乘也可以表示为矩阵的相乘，如果我们有两 b a b a 3

个复数 z1 = a + bi, z2 = c + di，那么与 z1z2 所代表的变换则可以表示为： 24a −b 3524c −d 35 24ac − bd −(bc + ad) d b a c 35 bc + ad ac − bd z1z2 = = 注意，复数的相乘是满足交换律的，如果你自己尝试一下，就会发现 z1z2 与 z2z1 是等价的： 35 = z1z2 c a b d z2z1 = 24c −d 3524a −b 35 24ac − bd −(bc + ad) 除此之外，我们来看一下一些特殊复数的矩阵形式： 241 0 35 = I 35 240 −1 ac − bd bc + ad 0 1 1 = = i = 1 0 (a = 1, b = 0) (a = 0, b = 1) 240 −1 1 0 35，如可以看到，实数单位 1与单位矩阵是等价的．而虚数单位 i则等价于果我们尝试对它进行平方，可以发现： 35 = −I = −1 35240 −1 240 −1 24−1 35 = i2 = i · i = 0 0 −1 1 0 1 0 即便是在矩阵形式下，i2 与 −1其实也是等价的，这进一步展示了复数与这一矩阵形式的关联． 4

1.2.3 复数的模长与共轭在进行下一步的讨论之前，我们先定义一下复数的模长（Magnitude）．如果 z = a + bi，那么它的模长为： p ∥z∥ = a2 + b2 接下来，我们定义复数的共轭（Conjugate）．如果 z = a + bi，那么它的共轭为： z = a − bi 我们只需要翻转 z虚部的符号就能得到它的共轭了．如果我们尝试计算 zz，我们会发现： zz = (a + bi)(a − bi) = a2 − abi + abi + b2 = a2 + b2 = ∥z∥2 所以，一个复数的模长又可以通过乘积的方式进行计算： ∥z∥ = √ zz 35矩阵所作出的变 1.3 复数相乘与 2D旋转现在，我们回到之前的话题，既然与复数的相乘代表着换，那这种变换代表着什么呢？实际上，如果我们对这个矩阵进行一些变形，这个问题就很容易解决了： 24a −b 24 a√ 我们将矩阵中每一个元素都除以了模长 ∥z∥ = 外面．经过这一变换，我们只需要观察一下复平面就能够解答之前的问题了： 35 = −b√ a2+b2 a√ a b 24a −b 35 a2 + b2 a2+b2 b√ a2+b2 √ p b a a2+b2 a2 + b2，并将这一项提到了矩阵 5

Im bi z = a + bi √ a2 + b2 θ a b a Re b a sin(θ) p 35 = 可以看到，∥z∥ 正是复数 z 与坐标轴所形成的三角形的斜边长，而 a, b 分别为三角形的两个直角边．如果将斜边与实数轴 Re 正方向的夹角记为 θ 的话，按照三角函数的定义可以得出 a√ a2+b2 = sin(θ)，这个角度 θ 其实就是 a2+b2 = cos(θ)，且 b√ atan2(b, a)．知道了这些，原矩阵就可以变形为： 24a −b 24cos(θ) − sin(θ) 35 24cos(θ) − sin(θ) 35 24cos(θ) − sin(θ) 35 3524cos(θ) − sin(θ) 24∥z∥ (对任意方形矩阵 A = IA) = ∥z∥ · I = ∥z∥ a2 + b2 35 cos(θ) cos(θ) cos(θ) 0 sin(θ) cos(θ) 24∥z∥ 35则是我们熟悉的 2D旋转矩阵． 24cos(θ) − sin(θ) 我们将原本的矩阵变形为了两个变换矩阵的复合，其中左边的矩阵，而右边的即便你不认识后面的那个旋转矩阵也没有关系，我们可以看看这个矩阵对两个基 35是缩放 0 ∥z∥ cos(θ) sin(θ) 0 sin(θ) sin(θ) 0 ∥z∥ = 6

0 sin(θ) = sin(θ) 35 0 0 0 b a 0 sin(θ) cos(θ) 0 ∥z∥ 0 ∥z∥ 240 1 241 0 241 35和 35241 35 第一步首先将 35： 241 35的变换效果．首先是 24∥z∥ 35 = 35241 24a −b 3524cos(θ) − sin(θ) 24∥z∥ 3524cos(θ) 35变换到了 24cos(θ) 35的位置，也就是逆时针旋转了 θ度，接下来： 24∥z∥ 3524cos(θ) 35 = 24∥z∥ cos(θ) 24cos(θ) 24∥z∥ cos(θ) 35缩放了 ∥z∥倍，变为缩放矩阵将 35： 240 逆时针旋转了 θ 度，并缩放了 ∥z∥倍．接下来是 24∥z∥ 24a −b 24∥z∥ 24− sin(θ) 35 变换到了 3524cos(θ) − sin(θ) 3524− sin(θ) 35 的位置，这同样是逆时针旋转了 θ 度， 35 35．总的来说，就是对 35240 35 35240 35 = 241 35 ∥z∥ sin(θ) ∥z∥ sin(θ) sin(θ) cos(θ) 0 ∥z∥ 0 ∥z∥ b a 1 0 ∥z∥ 0 sin(θ) 0 0 = 0 1 35 cos(θ) sin(θ) 1 0 240 1 这里，第一步将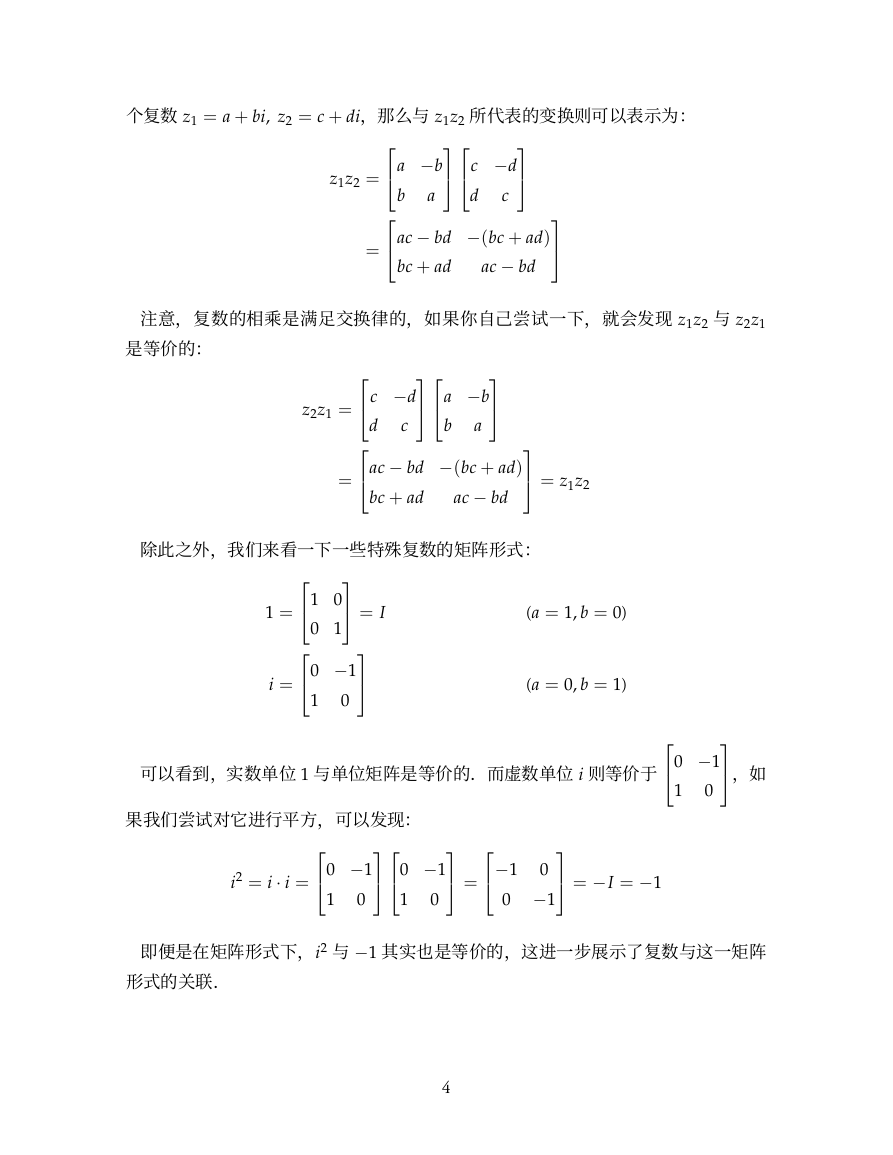见下图： cos(θ) 7

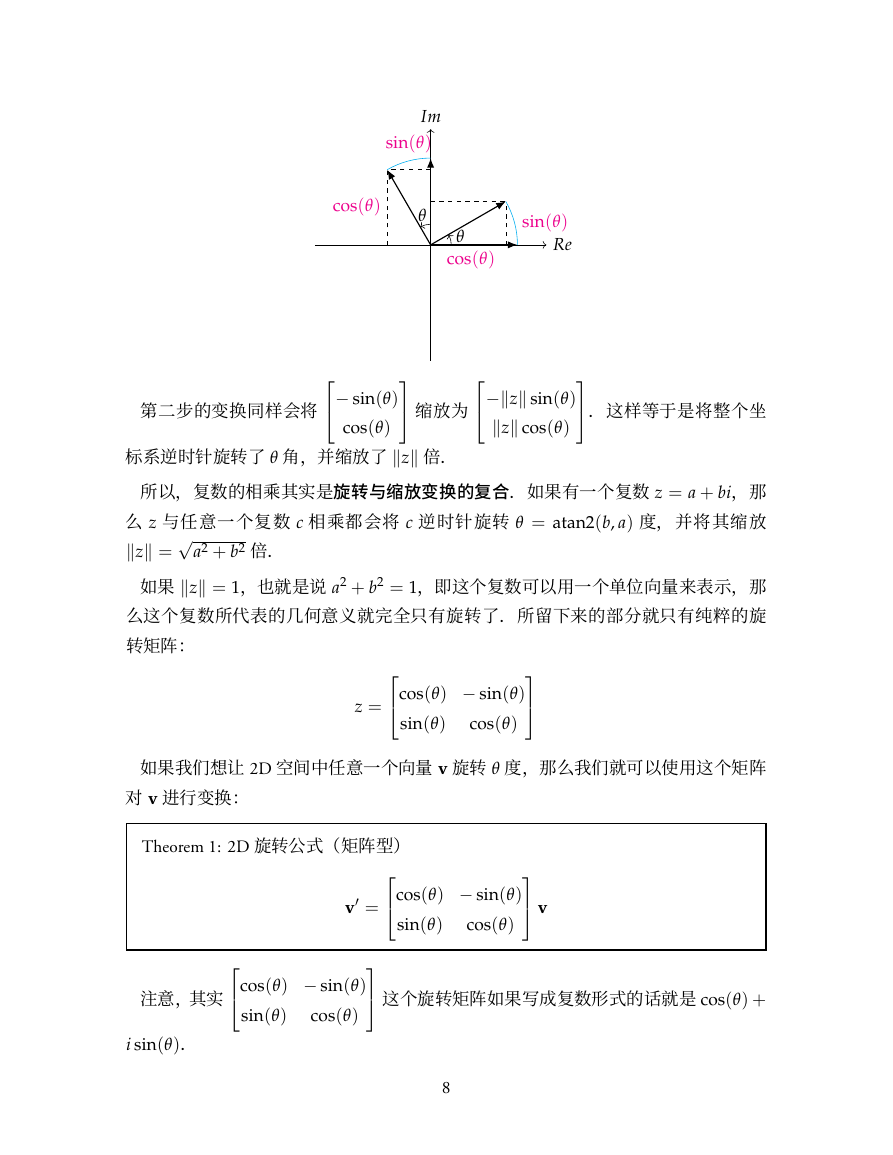
Im sin(θ) cos(θ) θ sin(θ) Re θ cos(θ) cos(θ) ∥z∥ cos(θ) 24− sin(θ) 24−∥z∥ sin(θ) 35缩放为 35．这样等于是将整个坐第二步的变换同样会将标系逆时针旋转了 θ 角，并缩放了 ∥z∥倍．所以，复数的相乘其实是旋转与缩放变换的复合．如果有一个复数 z = a + bi，那么 z 与任意一个复数 c 相乘都会将 c 逆时针旋转 θ = atan2(b, a) 度，并将其缩放 ∥z∥ = 如果 ∥z∥ = 1，也就是说 a2 + b2 = 1，即这个复数可以用一个单位向量来表示，那么这个复数所代表的几何意义就完全只有旋转了．所留下来的部分就只有纯粹的旋转矩阵： a2 + b2 倍． √ 24cos(θ) − sin(θ) 35 z = sin(θ) cos(θ) 如果我们想让 2D空间中任意一个向量 v旋转 θ 度，那么我们就可以使用这个矩阵对 v进行变换： Theorem 1: 2D旋转公式（矩阵型） 24cos(θ) − sin(θ) 24cos(θ) − sin(θ) 35这个旋转矩阵如果写成复数形式的话就是 cos(θ) + 35 v cos(θ) sin(θ) = v ′ 注意，其实 i sin(θ)． sin(θ) cos(θ) 8

资料库

quaternion.pdf

相关推荐

游戏开发

热门标签

最新资料