‹ 9 ‹ 9 ‹ ‹ 　　　　　　　　　　　　　　　　　　Industrial Furnace 　　　　　　　Vol. 27 　No. 3 　May 2005 　　　文章编号 :1001 - 6988 (2005) 03 0032 04 MA TLAB 在求解温度场中的应用 李 　萍 ,张 　薇 (南京工业大学 材料科学与工程学院 , 江苏 南京 210009) 摘 　要 :介绍了如何用 MA TLAB 中的 PDE 工具箱来求解一般导热问题 。借助于 PDE 工具箱 ,不需编程 ,直接进入 用户图形界面 ( GU I) 对实际工程问题进行求解 。通过对平壁点热源导热算例的分析表明 , PDE 工具箱求解一般问题快 捷 、简单 。文中并提及了点热源导热模型的工程应用价值 。 关键词 :温度场 ; PDE 工具箱 ;非稳态导热 ;点热源 中图分类号 : T K124 　　　文献标识码 : A Application of MATLAB in Solving Temperature Field ( College of M aterials Science and Engi neeri ng , N anji ng U niversity of Technology , N anji ng 210009 , Chi na) L I Ping , ZHAN G Wei Abstract : The question t hat how to solve general heat transfer problems wit h PDE tool box in MA T t program and can enter t he GU I directly to solve practical LAB is introduced. By PDE tool box , you needn s heat transfer , t he result engineering problem. By analyzing t he example of slab wit h t he point heat source shows t hat it is raopid and simple by using PDE tool box to solve common problem. The engineering impor tance about t he point heat source heat transfer model is also mentioned. Key words : temperature field ; PDE tool box ; non steady state heat conduction ; point heat source 1 　概 　述 2 　PDE 工具箱简介 在科学工程和生产实际中 ,常常需要确定固体 材料内部的温度场 ,因而研究特殊非稳态导热尤为 重要 。一般非稳态导热问题的控制方程为多维非线 性方程 ,再结合定解条件 (初始条件 、边界条件) 求 解 。对于简单的边界条件可以直接求得理论解 ,而 对不规则外形和复杂边界条件多用数值解法 。一般 软件都是将时间 、空间坐标划分为许多的网格 ,然后 借助于计算机编程求解 。而利用 MA TLAB 中的 PDE 工具箱 ,无需编程则可直接对特殊边界条件的 非稳态导热问题进行求解 。 收稿日期 :2005 - 02 - 25 作者简介 :李 　萍 (1980 —) ,女 ,硕士研究生 ,从事新材料热物性 的测定和研究工作. 23 MA TLAB 中的偏微分方程 ( PDE) 工具箱是用 有限元法求解偏微分方程得到数值近似解 ,可以求 解线性的椭圆型 、抛物线型 、双曲线型偏微分方程及 本征型方程和简单的非线性偏微分方程 ,具体可处 理数学模型形式如下 : 椭圆型 PDE - ·( c u) + ɑu = f 非线性 PDE - ·( c ( u) u) + ɑ( u) u = f ( u) 本征型问题 - ·( c 抛物线型 PDE u) + ɑu = ε·du d ( u/ t) - ·( c u) + ɑu = f (1) (2) (3) (4) © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

《工 　业 　炉》　第 27 卷 　第 3 期 　2005 年 5 月 辑 ,可得到自己想要的形式和数据 ,这是教材中未曾 说明过的 。 有了上述对 PDE 工具箱使用的知识 ,就可以结 合实例来说明该工具箱解决传热问题的优势 。 4 　用 PDE 工具箱求解温度场 温度场中用来描述三维非稳态导热微分方程的 一般形式为 : ρc T t = (λ y T y ) + (λ (λ x z T x T z ) + + Φ (6) 其中 :ρ、c 、λ和Φ 各为微元体的密度 、比热容 、导热 系数及单位时间单位体积中内热源的生成热 , t 为 时间 。要通过控制方程 (6) 获得某一具体导热问题 的温度分布 ,需要结合定解条件 (初始条件 、边界条 件) 来求解 ,通过下面的点热源导热模型来体现 。 已知一无限大平壁厚 0. 3 m (设为钢筋混凝土 材料) ,密度ρ= 2 400 kg/ m3 ,比热 C = 0. 84 kJ / (kg ·K) ,导热系数 λ= 1. 54 W/ ( m·K) ,整个平壁初始 温度 T1 = 20 ℃,现以一恒流点热源 (2 000 W/ m2) 对平壁一边进行加热 ,热源一面除了热源点之外 ,边 界条件有两类 :恒流 (热流为零) 和对流换热 。与空 气的对流换热系数 h = 5 W/ (m2·K) ,其它面恒温为 20 ℃,分析温度场变化情况 ,物理模型如图 1 所示 。 图 1 　物理模型示意图 　　在恒定热流的热源作用下 ,平壁缓慢升温 ,壁内 可以看作二维导热过程 ,坐标选取如图 2 所示 。 双曲线型 PDE d ( 2 u/ ·( c 式中 : u —域 Ω 上求解变量 t 2) - u) + ɑu = f (5) t —时间变量 ε—特征值 c 、a 、f —常数或者变量 上述几种数学模型多在热传导 、电磁学和声学 的波传导等问题求解中应用 。 3 　导热问题的 MATLAB 求解法 对于大多数导热问题 ,求解温度场时很难得到 解析解 ,只能利用计算机得到数值解来无限接近代 替精确解 。数值解方法又有有限元法 、有限差分法 、 混合微分差分法 、离散元法 、拉格朗日元法等 ,其中 有限元法是利用部分插值把区域连续求解的微分方 程离散成求解线性代数方程组 。在使用 MA TLAB 的 PDE 工具箱进行有限元计算前需要有一些预处 理的工作 ,如对所求解模型的几何形状或者形体进 行离散化 ,即用比较简单的形状和形体来逼近和代 替实际的形状和形体 ,这样可以把比较复杂的曲线 和曲面问题转化为相对简单的直线或平面问题 。 在实际求解温度场时 ,可以直接进入 pdetool , 利用图形用户界面 ( GU I) 来求解偏微分方程 。首先 选择导热模型 ,建立一个用来描述对应导热问题的 物理模型 。然后根据需要对求解问题赋予边界条 件 ,即对命令函数 pdesetbd 进行设定 ( MA TLAB 指 定了如下 3 种边界条件 : ①Dirichlet 条件 , hu = r ; ②广义 Neumann 条件 , n·( c u) + qu = g ; ③混合 边界条件 ,Dirichlet 条件和 Neumann 条件的组合 。 式中 n 为垂直于边界的单位矢量 , h 、r 、q 、g 为常 量或与 u 有关的变量) 。其次 ,确定偏微分方程的类 型 ,结合已知条件设定方程参数 。再次 ,利用函数 init mesh 和 refinemesh 创建初始三角形网格以及细 化网格 。最后 ,直接使用算法函数求解偏微分方程 。 此外 , PDE 工具箱提供了多种可视化结果的方法 , 有平面图 、网格 图 、等 高 线 图 、矢 量 图 , 可 以 表 示 temperature 、heat flux 、temperature gradient 。对于抛 物线型和双曲线型偏微分方程 ,该工具箱还可给出 方程解随时间变化的动画程序 。通过对图形的编 © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 图 2 　坐标选取示意图 33 

计算机控制与应用 :MA TLAB 在求解温度场中的应用 　　结合使用 PDE 工具箱求解导热问题的一般方 法 ,对上述点热源的温度场求解分别进行几何模型 设定 、初始条件和边界条件带入 、网格划分 、方程设 定及求解方程[ 4 ] ,其结果分析如下 : 式 (6) 适用一般非稳态导热的数学模型 ,应用于 平壁点热源导热模型的 Parabolic 方程为 : rho ×C × T′- div ( k ×grɑd ( T) ) = Q + h ×( Text - T ) , El liptic 方程为 - div ( k ×grɑd ( T) ) = Q + h ×( Text - T) ,图 3 为网格精化图 ,图 4 为采用 Elliptic 模型得 到的平壁点热源导热温度分布三维图 ,即为稳定时 的温度场 。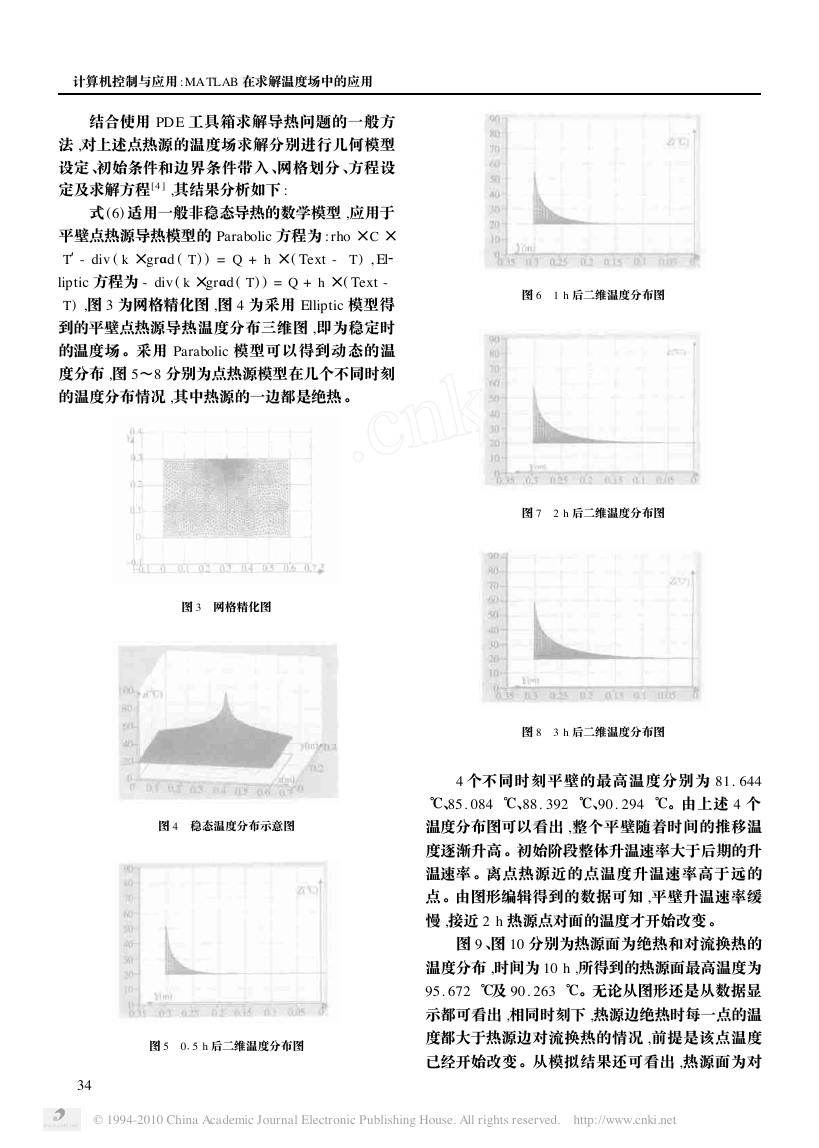采用 Parabolic 模型可以得到动态的温 度分布 ,图 5～8 分别为点热源模型在几个不同时刻 的温度分布情况 ,其中热源的一边都是绝热 。 1 图 6 　1 h 后二维温度分布图 图 7 　2 h 后二维温度分布图 图 3 　网格精化图 图 4 　稳态温度分布示意图 图 5 　0 5 h 后二维温度分布图 43 图 8 　3 h 后二维温度分布图 4 个不同时刻平壁的最高温度分别为 81. 644 ℃、85. 084 ℃、88. 392 ℃、90. 294 ℃。由上述 4 个 温度分布图可以看出 ,整个平壁随着时间的推移温 度逐渐升高 。初始阶段整体升温速率大于后期的升 温速率 。离点热源近的点温度升温速率高于远的 点 。由图形编辑得到的数据可知 ,平壁升温速率缓 慢 ,接近 2 h 热源点对面的温度才开始改变 。 图 9 、图 10 分别为热源面为绝热和对流换热的 温度分布 ,时间为 10 h ,所得到的热源面最高温度为 95. 672 ℃及 90. 263 ℃。无论从图形还是从数据显 示都可看出 ,相同时刻下 ,热源边绝热时每一点的温 度都大于热源边对流换热的情况 ,前提是该点温度 已经开始改变 。从模拟结果还可看出 ,热源面为对 © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net 

流换热时其温升规律和绝热的温升规律是一致的 。 图 9 　热源边绝热 10 h 后二维温度分布图 图 10 　热源边对流换热 10 h 后二维温度 分布图 5 　结论 研究温度场的分布在工程领域中有重要的作 用 。本文中提及的点热源模型对研究焊接过程中因 温度分布所引起的应力问题具 有 重 要 的 实 际 意 义[ 1 ] 。延伸到线热源 、面热源模型的模拟 ,可以帮 助解决热物性参数测试中的一些问题 ,如以物体表 面温度推算变导热系数的测试原理及技术[2 ] 。此外 , 《工 　业 　炉》　第 27 卷 　第 3 期 　2005 年 5 月 工程上需要温度的在线检测情况很多 ,能够对温度 场进行预先模拟 ,对测试有较好的指导意义 。 从上述使用 PDE 工具箱求解点热源导热模型 的结果可以看出使用 MA TLAB 的快捷灵活 。若自 己编程 ,过程复杂麻烦 。当步长选取不当会导致求 解结果发散或振荡 。因而结合 PDE 工具箱直接调 用其中网格划分 、求解方程的命令来求解温度场可 以快速得到理想的结果 。 PDE 工具箱只能在二维空间上求解 ,但结合大 多数工程问题的对称性 ,可以对模型进行转化处理 , 选取代表性的截面来分析 ,本文的例题就是采用了 这样的做法 。在 GU I 上可以处理复杂几何形状的 导热问题 ,如多种物性参数材料的叠加或嵌入[ 3 ] , 这是一般的程序很难用语言描述的 。有了网格的精 化 ,使得有限元数值解的精度大大提高 , MA TLAB 使用灵活 ,易于修改 ,这是其它语言无法比拟的 。 因而可见 ,使用 MA TLAB 的 PDE 工具箱可以 方便快速地解出特殊几何形状和复杂边界条件的导 热问题 ,多种可视化图形使得结果便于理解 ,也为工 程上一些实际导热问题提供了解决方法 。 参考文献 : [ 1 ] 　黄惠兰 ,喻锡臣. 薄板点热源加热的有限元分析[J ] . 广西大学 学报 (自然科学版) ,2002 , (2) :114 - 116. [ 2 ] 　路勇 ,宁智. 以表面温度推算变导热系数的测试原理及技术 [J ] . 计量学报 ,1995 , (1) :53 - 57. [ 3 ] 　李维刚 ,朱先富. PDE 工具箱在静磁场中的应用[J ] . 机车电传 动 ,2003 , (4) :29 - 32. [ 4 ] 　苏金明 ,张莲花 ,刘波. MATLAB 工具箱应用[ M ] . 北京 :电子 工业出版社 ,2004. [ 5 ] 　俞昌铭. 热传导及数值分析[ M ] . 北京 :清华大学出版社 ,1981. [ 6 ] 　何仁斌. MATLAB6 工程计算及应用[ M ] . 重庆 :重庆大学出 版社 ,2001. 国外科技文摘 WZ 0513 　滴管炉中煤的高压热解作用 。K. Mat suoka , et al . High pressure coal pyrolysis in a drop tube furnace. Energy & Fuels (能源与燃料 ,美国) . 2003 ,17 (4) : 984 - 990 (英文) 。 利用滴管炉进行煤的高压连续热解实验 ,以便 获得有用和可靠的热解数据 。仔细检测煤热解时的 质量平衡 ,可了解数据的可靠性 。在该设备中获得 的煤热解数据与先前的实验结果进行比较 ,发现滴 管炉中重量损耗大于其它设备的重量损耗 。实验结 果与 3 种热解模型中预计结果比较时 ,在某种情况 下预计结果与实验结果存在差异 ,但是在 800 ℃和 1 MPa 下 ,3 种热解模型中预计值与实验重量损耗 值十分符合 。 53 © 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net