字典学习KSVD.doc-资料库

1ba09246-7dc9-40ec-9ca9-faab152c295b.doc.pdf-第1页.png

第1页 / 共14页

1ba09246-7dc9-40ec-9ca9-faab152c295b.doc.pdf-第2页.png

第2页 / 共14页

1ba09246-7dc9-40ec-9ca9-faab152c295b.doc.pdf-第3页.png

第3页 / 共14页

1ba09246-7dc9-40ec-9ca9-faab152c295b.doc.pdf-第4页.png

第4页 / 共14页

1ba09246-7dc9-40ec-9ca9-faab152c295b.doc.pdf-第5页.png

第5页 / 共14页

1ba09246-7dc9-40ec-9ca9-faab152c295b.doc.pdf-第6页.png

第6页 / 共14页

1ba09246-7dc9-40ec-9ca9-faab152c295b.doc.pdf-第7页.png

第7页 / 共14页

1ba09246-7dc9-40ec-9ca9-faab152c295b.doc.pdf-第8页.png

第8页 / 共14页

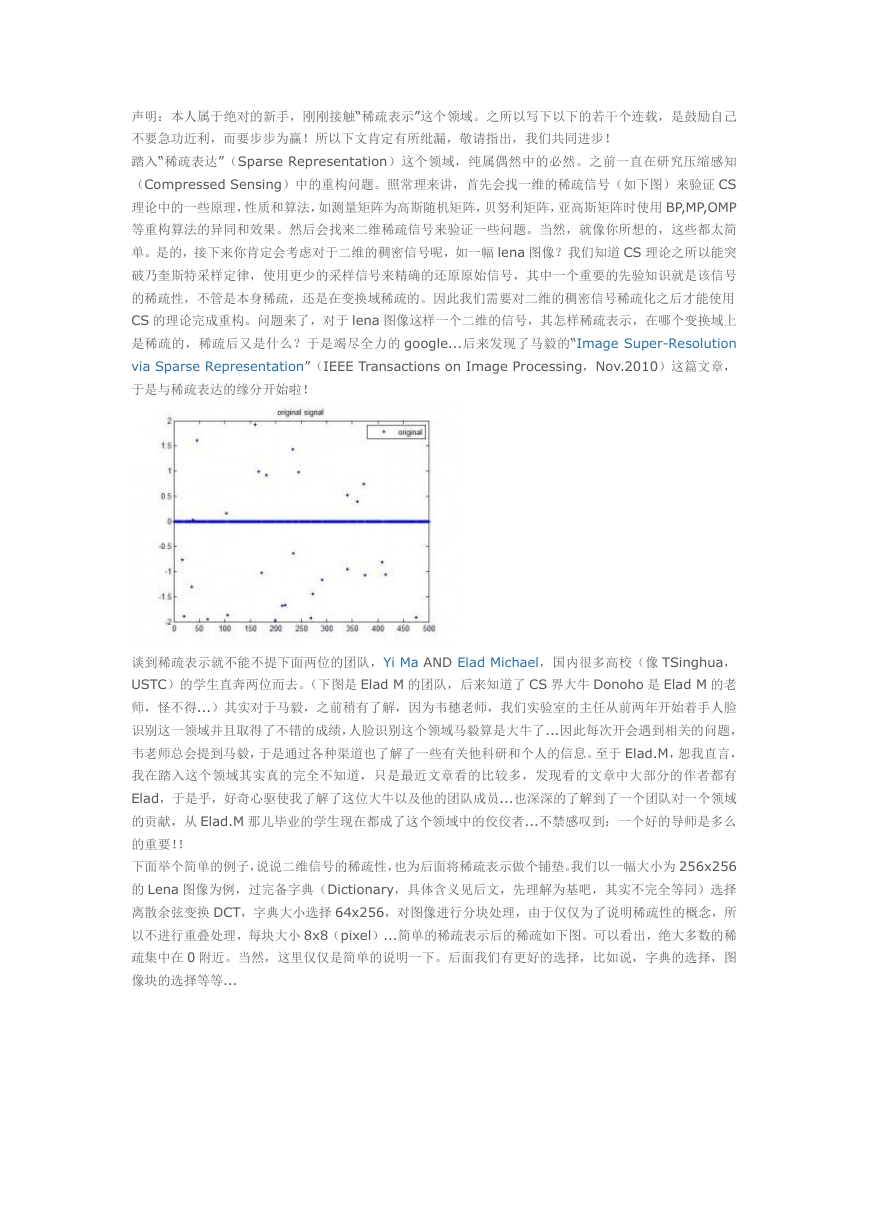
声明：本人属于绝对的新手，刚刚接触“稀疏表示”这个领域。之所以写下以下的若干个连载，是鼓励自己不要急功近利，而要步步为赢！所以下文肯定有所纰漏，敬请指出，我们共同进步！踏入“稀疏表达”（Sparse Representation）这个领域，纯属偶然中的必然。之前一直在研究压缩感知（Compressed Sensing）中的重构问题。照常理来讲，首先会找一维的稀疏信号（如下图）来验证 CS 理论中的一些原理，性质和算法，如测量矩阵为高斯随机矩阵，贝努利矩阵，亚高斯矩阵时使用 BP,MP,OMP 等重构算法的异同和效果。然后会找来二维稀疏信号来验证一些问题。当然，就像你所想的，这些都太简单。是的，接下来你肯定会考虑对于二维的稠密信号呢，如一幅 lena 图像？我们知道 CS 理论之所以能突破乃奎斯特采样定律，使用更少的采样信号来精确的还原原始信号，其中一个重要的先验知识就是该信号的稀疏性，不管是本身稀疏，还是在变换域稀疏的。因此我们需要对二维的稠密信号稀疏化之后才能使用 CS 的理论完成重构。问题来了，对于 lena 图像这样一个二维的信号，其怎样稀疏表示，在哪个变换域上是稀疏的，稀疏后又是什么？于是竭尽全力的 google...后来发现了马毅的“Image Super-Resolution via Sparse Representation”（IEEE Transactions on Image Processing，Nov.2010）这篇文章，于是与稀疏表达的缘分开始啦！谈到稀疏表示就不能不提下面两位的团队，Yi Ma AND Elad Michael，国内很多高校（像 TSinghua， USTC）的学生直奔两位而去。（下图是 Elad M 的团队，后来知道了 CS 界大牛 Donoho 是 Elad M 的老师，怪不得...）其实对于马毅，之前稍有了解，因为韦穗老师，我们实验室的主任从前两年开始着手人脸识别这一领域并且取得了不错的成绩，人脸识别这个领域马毅算是大牛了...因此每次开会遇到相关的问题，韦老师总会提到马毅，于是通过各种渠道也了解了一些有关他科研和个人的信息。至于 Elad.M，恕我直言，我在踏入这个领域其实真的完全不知道，只是最近文章看的比较多，发现看的文章中大部分的作者都有 Elad，于是乎，好奇心驱使我了解了这位大牛以及他的团队成员...也深深的了解到了一个团队对一个领域的贡献，从 Elad.M 那儿毕业的学生现在都成了这个领域中的佼佼者...不禁感叹到：一个好的导师是多么的重要！！下面举个简单的例子，说说二维信号的稀疏性，也为后面将稀疏表示做个铺垫。我们以一幅大小为 256x256 的 Lena 图像为例，过完备字典（Dictionary，具体含义见后文，先理解为基吧，其实不完全等同）选择离散余弦变换 DCT，字典大小选择 64x256，对图像进行分块处理，由于仅仅为了说明稀疏性的概念，所以不进行重叠处理，每块大小 8x8（pixel）...简单的稀疏表示后的稀疏如下图。可以看出，绝大多数的稀疏集中在 0 附近。当然，这里仅仅是简单的说明一下。后面我们有更好的选择，比如说，字典的选择，图像块的选择等等...

2. 压缩感知（CS），或许你最近听说的比较多，不错，CS 最近比较火，什么问题不管三七二十一就往上粘连，先试试能不能解决遇到的问题，能的话就把文章发出来忽悠大家，这就是中国学术浮躁的表现...我们没有时间去思考的更多，因为你一思考，别人可能就把“你的东西”抢先发表了...不扯了，反正也干预不了... 稀疏表示的现状有点像 CS，能做很多事，也不能做很多事...但是它确实是解决一些棘手问题的方法，至少能提供一种思路...目前用稀疏表示解决的问题主要集中在图像去噪（Denoise），代表性 paper：Image Denoise Via Sparse and Redundant Representations Over Learned Dictionaries(Elad M. and Aharon M. IEEE Trans. on Image Processing,Dec,2006); Image Sequence Denoising Via Sparse and Redundant Representations(Protter M. and Elad M.IEEE Trans. on Image Processing,Jan,2009)，还有超分辨率（Super-Resolution OR Scale-Up），代表性 paper：Image Super-Resolution via Sparse Representation（Jianchao Yang, John Wright, Thomas Huang, and Yi Ma，IEEE Transactions on Image Processing, Nov,2010）, A Shrinkage Learning Approach for Single Image Super-Resolution with Overcomplete Representations( A. Adler, Y. Hel-Or, and M. Elad,ECCV,Sep,2010).... 另外还有 inpait，deblur，Face Recognition，compression 等等..更多应用参考 Elad M 的书，google 能找到电子档，这里不提供下载地址

当然 Elad M.和 Yi Ma 的团队不仅仅在应用上大做文章，在理论上也是不断革新...就拿字典学习为例，一开始将固定字典（如过完备 DCT，Contourlet，Wavelet 字典）用在去噪，超分辨率上，效果不明显，可能某些情况下还不如空域或者频域的去噪效果好（我拿 Lena 图像和 DCT 实验了，以 PSNR 为标准，比时域的去噪方法要好，但是比小波去噪相比，稍稍逊色），但是速度快是它的优点。于是他们开始研究自适应的字典学习算法，开始使用很多图像进行学习，后来采用单幅图像进行学习来提高运算速度（使用很多图像进行学习属于半自适应的学习，对于自然图像的处理需要学习自然图像，对遥感图像的处理需要学习遥感图像，但是对自然图像或遥感图像的去噪，超分辨率处理，都可以使用已经训练好的相应的字典）；同时学习的方法也不尽相同，开始使用 MOD，后来就是一直比较流行的 K-SVD，最近又出来了 Online，总体而言 Online 比较快。下面是我提到的几种字典的例子，所有的字典都是 64x256 大小的，依次为 DCT， globally（训练图像是：标准图像 lena，boat，house，barbara，perppers），K-SVD（单幅含躁 lena，噪声标准差为 25），online（单幅含躁 lena，噪声标准差为 25），其中 globally 的训练方法是将训练图像分成 8x8 的 overlap patch，平均取，共取 10000 块，K-SVD 和 online 也是分成相同的重叠块，取所有可能的块。

总之，Elad M.和 Yi Ma 为稀疏表示这个领域作出了很大的贡献...向大牛们致敬！！最后稍微说一下国内的研究现状，国内的很多研究还没浮出水面，不知道是不是我想的的这样（我比较疑惑的是，为什么国外研究了十几年，国内还没大动静？），至少从 google 学术以及 IEEE 的文章搜索上来看是这样的...不过还是有几位教授在这方面作出了很大的贡献的... 3 我们来考虑信号的稀疏表示问题，假如我们有了过完备字典 D，如何求出信号 x 在这个过完备字典上的稀疏表示？先来回顾一下在压缩感知中常常会遇到的问题，信号 x 在经过测量矩阵 A 后得到测量值 y，即 y=A*x，其中测量矩阵 A_mxn(m 远小于 n)，那么怎样从 y 中精确的恢复出 x 呢？由于 m 远小于 n，用 m 个方程求解 n 个未知数，因此 y=A*x 是个欠定方程，有无穷多个解。就像我们解优化问题一样，如果我们加上适当的限定条件，或者叫正则项，问题的解会变得明朗一些！这里我们加上的正则项是 norm(x,0)，即使重构出的信号 x 尽可能的稀疏（零范数：值为 0 的元素个数），后来 Donoho 和 Elad 这对师徒证明了如果 A 满足某些条件，那么 argmin norm(x,0) s.t.y=A*x 这个优化问题即有唯一解！唯一性确定了，仍然不能求解出该问题，后来就尝试使用 l1 和 l2 范数来替代 l0 范数，华裔科学家陶哲轩和 candes 合作证明了在 A 满足 UUP 原则这样一个条件下，l0 范数可以使用 l1 范数替代，所以优化问题变成 argmin norm(x,1) s.t.y=A*x 这样一个凸优化问题，可以通过线性优化的问题来解决！（参考文献：Stable signal recovery from incomplete and inaccurate measurements（E. J. Candès, J. Romberg and T. Tao））至此，稀疏表示的理论已经初步成型。至于之后的优化问题，都是一些变形，像 lasso 模型，TV 模型等....这里推荐一本 stanford 的凸优化教材 convex optimization，

我准备抽个时间好好看一看，搞稀疏表达这一块的，优化问题少不了...最近一直在感叹：数学不好的人哪伤不起啊！！有木有！！我们再回到我们一开始提到的问题上来，一开始说字典 D 已知，求出 y 在过完备字典 D 上的稀疏表示 x，这个在稀疏表示里面被称作为 Sparse Coding...问题的模型是 x=argmin norm(y-D*x,2)^2 s.t.norm(x,1)<=k;我们下面来介绍一下解决这个问题的惯用方法 OMP(Orthogonal Matching Pursuit) 我们主要目标是找出 x 中最主要的 K 个分量（即 x 满足 K 稀疏），不妨从第 1 个系数找起，假设 x 中仅有一个非零元 x(m)，那么 y0=D(:,m)*x(m)即是在只有一个主元的情况下最接近 y 的情况， norm(y-y0,2)/norm(y,2)<=sigma,换句话说在只有一个非零元的情况下，D 的第 m 列与 y 最“匹配”，要确定 m 的值，只要从 D 的所有列与 y 的内积中找到最大值所对应的 D 的列数即可，然后通过最小二乘法即可确定此时的稀疏系数。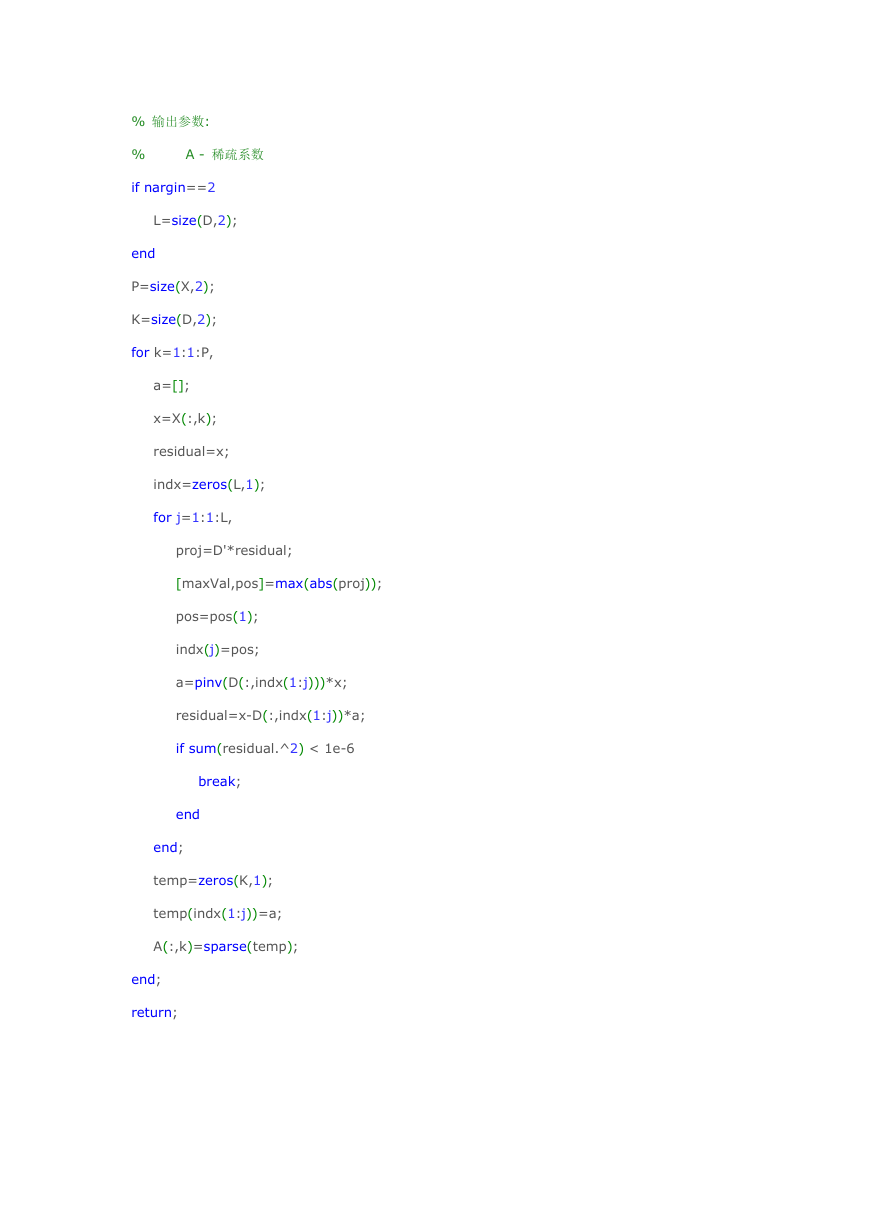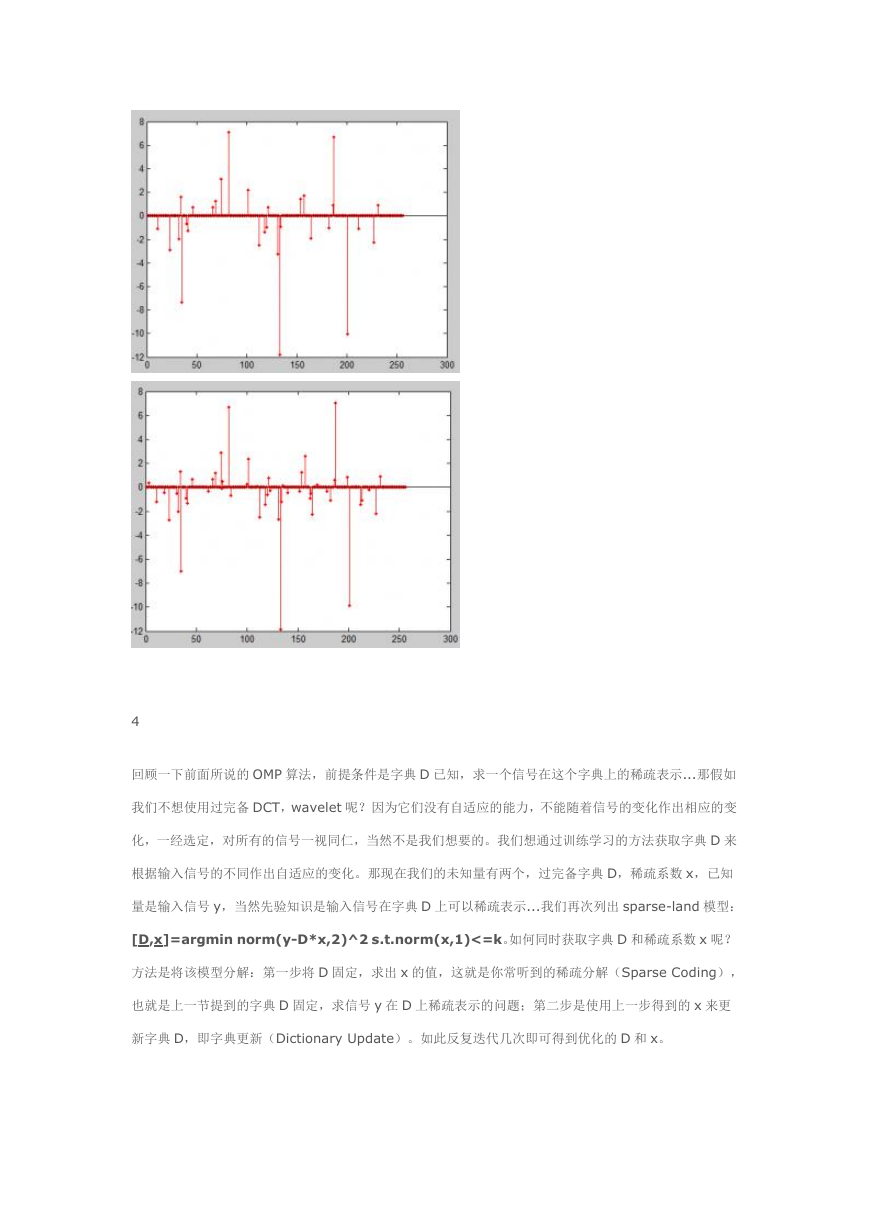考虑非零元大于 1 的情况，其实是类似的，只要将余量 r=y-y0 与 D 的所有列做内积，找到最大值所对应 D 的列即可。...下面是代码和示例结果[其中图 1 是 lena 图像某个 8x8 的图像块在其自身训练得到的字典上的稀疏表示，稀疏值 k=30，相对误差 norm(y-y0,2)/norm(y,2)=1.8724，图 2 是相同的块在相同的字典下的稀疏表述，稀疏值 k=50，相对误差为 0.0051] function A=OMP(D,X,L) % 输入参数: % % % D - 过完备字典，注意：必须字典的各列必须经过了规范化 X - 信号 L - 系数中非零元个数的最大值（可选，默认为 D 的列数，速度可能慢）

% 输出参数: % A - 稀疏系数 if nargin==2 L=size(D,2); end P=size(X,2); K=size(D,2); for k=1:1:P, a=[]; x=X(:,k); residual=x; indx=zeros(L,1); for j=1:1:L, proj=D'*residual; [maxVal,pos]=max(abs(proj)); pos=pos(1); indx(j)=pos; a=pinv(D(:,indx(1:j)))*x; residual=x-D(:,indx(1:j))*a; if sum(residual.^2) < 1e-6 break; end end; temp=zeros(K,1); temp(indx(1:j))=a; A(:,k)=sparse(temp); end; return;

4 回顾一下前面所说的 OMP 算法，前提条件是字典 D 已知，求一个信号在这个字典上的稀疏表示...那假如我们不想使用过完备 DCT，wavelet 呢？因为它们没有自适应的能力，不能随着信号的变化作出相应的变化，一经选定，对所有的信号一视同仁，当然不是我们想要的。我们想通过训练学习的方法获取字典 D 来根据输入信号的不同作出自适应的变化。那现在我们的未知量有两个，过完备字典 D，稀疏系数 x，已知量是输入信号 y，当然先验知识是输入信号在字典 D 上可以稀疏表示...我们再次列出 sparse-land 模型： [D,x]=argmin norm(y-D*x,2)^2 s.t.norm(x,1)<=k。如何同时获取字典 D 和稀疏系数 x 呢？方法是将该模型分解：第一步将 D 固定，求出 x 的值，这就是你常听到的稀疏分解（Sparse Coding），也就是上一节提到的字典 D 固定，求信号 y 在 D 上稀疏表示的问题；第二步是使用上一步得到的 x 来更新字典 D，即字典更新（Dictionary Update）。如此反复迭代几次即可得到优化的 D 和 x。

Sparse Coding：x=argmin norm(y-D*x,2) s.t.norm(x,1)<=k Dictinary Update:D=argmin norm(y-D*x,2)^2 我们主要通过实例介绍三种方法：MOD，K-SVD,Online... 首先是 MOD(Method of Optimal Direction)。Sparse Coding 其采用的方法是 OMP 贪婪算法， Dictionary Update 采用的是最小二乘法，即 D=argmin norm(y-D*x,2)^2 解的形式是 D=Y*x'*inv(x*x’)。因此 MOD 算法的流程如下：初始化：字典 D_mxn 可以初始化为随机分布的 mxn 的矩阵，也可以从输入信号中随机的选取 n 个列向量，下面的实验我们选取后者。注意 OMP 要求字典的各列必须规范化，因此这一步我们要将字典规范化。根据输入信号确定原子 atoms 的个数，即字典的列数。还有迭代次数。主循环： Sparse Coding 使用 OMP 算法；Dictionary Update 采用最小二乘法。注意这一步得到的字典 D 可能会有列向量的二范数接近于 0，此时为了下一次迭代应该忽略该列原子，重新选取一个服从随机分布的原子。下面是使用 MOD 算法进行去噪的程序，首先是 MOD 算法，后面是将一幅 256x256 的图像进行去噪的程序，训练图像是含躁图像本身，采用重叠块的形式取块大小为 8x8，字典大小为 64x256，噪声标准差为 20. function [A,x]= MOD(y,codebook_size,errGoal) %============================== %input parameter % y - input signal % codebook_size - count of atoms %output parameter % A - dictionary % x - coefficent %============================== if(size(y,2)

资料库

字典学习KSVD.doc

相关推荐

行业

热门标签

最新资料