华南师范大学本科生实验报告
姓名_林少油 _
学号 20102100076
院系_计算机学院_ 专业_嵌入式 _
年级 2010 级
班级_3 班
小组实验任务分工_ 独立完成
实验时间
2012 年_5 月 12_日
实验名称
动态规划的应用
指导老师及职称 陈卫东 副教授
华南师范大学教务处编印
�
实验课程:算法分析与设计
实验名称:用动态规划法求解资源分配问题
(验证型实验)
实验目标:
(1)掌握用动态规划方法求解实际问题的基本思路。
(2)进一步理解动态规划方法的实质,巩固设计动态规划算法的基本步骤。
实验任务:
(1)设计动态规划算法求解资源分配问题,给出算法的非形式描述。
(2) 在 Windows 环境下用 C 语言实现该算法。计算 10 个实例,每个实例中 n=30, m=10,
Ci j 为随机产生于范围(0,103)内的整数。记录各实例的数据及执行结果(即最优分配方
案、最优分配方案的值)、运行时间。
(3)从理论上分析算法的时间和空间复杂度,并由此解释相应的实验结果。
实验设备及环境:
PC;C/C++等编程语言。
实验主要步骤:
(1) 根据实验目标,明确实验的具体任务;
(2) 分析资源分配问题,获得计算其最优值的递推计算公式;
(3) 设计求解问题的动态规划算法,并编写程序实现算法;
(4) 设计实验数据并运行程序、记录运行的结果;
(5) 分析算法的时间和空间复杂度,并由此解释释相应的实验结果;
问题分析:
问题描述:
某厂根据计划安排,拟将 n 台相同的设备分配给 m 个车间,各车间获得这种设备后,
可以为国家提供盈利 Ci j(i 台设备提供给 j 号车间将得到的利润,1≤i≤n,1≤j≤m) 。问如
何分配,才使国家得到最大的盈利?
算法基本思想:
本问题是一简单资源分配问题,由于具有明显的最优子结构,故可以使用动态规划求解,
用 状 态 量 f[i][j] 表 示 用 i 台 设 备 分 配 给 前 j 个 车 间 的 最 大 获 利 , 那 么 显 然 有 f[i][j] =
max{ f[k][j–1] + c[i-k][j] },0<=k<=i。再用 p[i][j]表示获得最优解时第 j 号车间使用的设备数
为 i-p[i][j],于是从结果倒推往回求即可得到分配方案。程序实现时使用顺推,先枚举车间
数,再枚举设备数,再枚举状态转移时用到的设备数,简单 3 重 for 循环语句即可完成。时
间复杂度为 O(n^2*m),空间复杂度为 O(n*m),倘若此题只需求最大获利而不必求方案,则
状态量可以减少一维,空间复杂度优化为 O(n)。
程序代码:
�
#include
#include
#include
#include
#include
using namespace std;
#define N 31
#define M 11
int c[N][M], f[N][M], p[N][M];
int main() {
int
i, j, n, m, k;
srand(time(NULL));
n = 30; m = 10;
for (int cas = 1; cas <= 5; ++cas) {
cout<<"实例"<




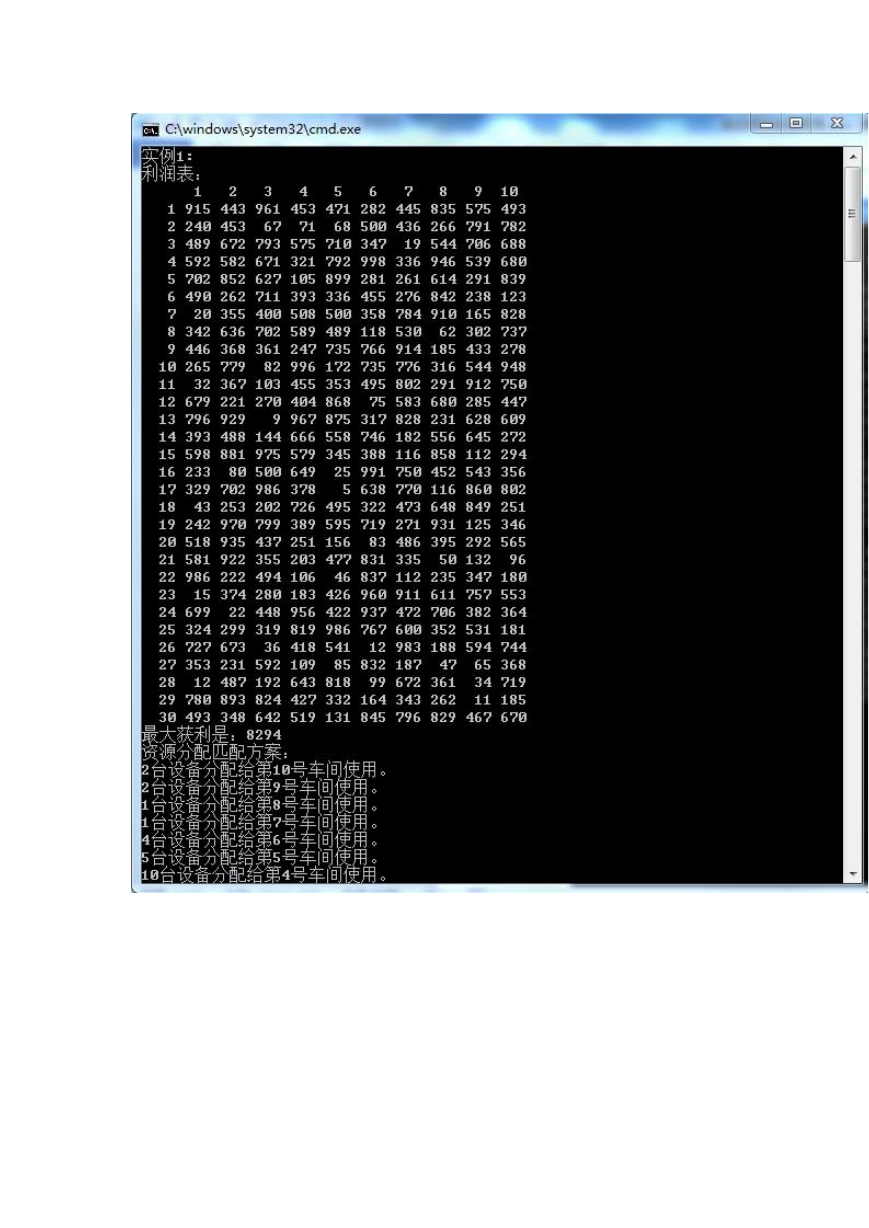
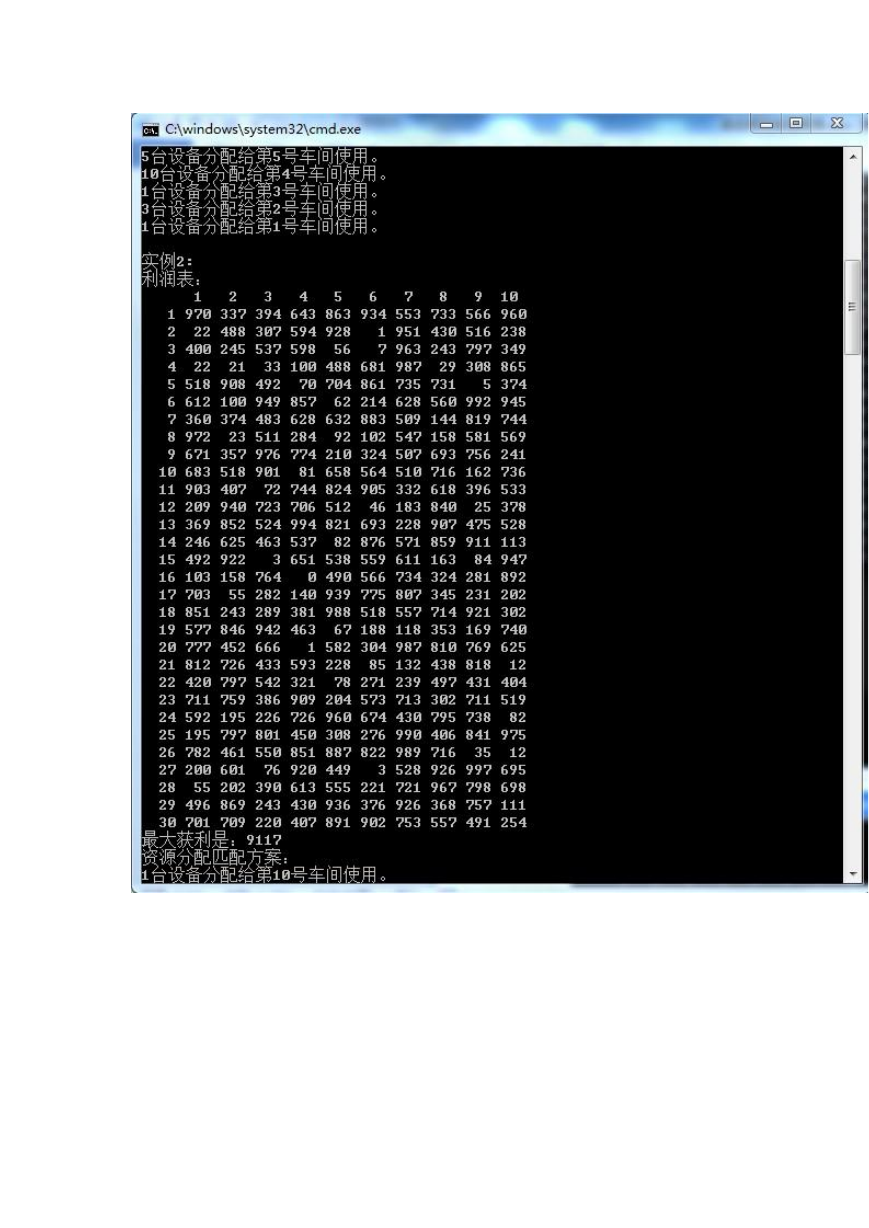
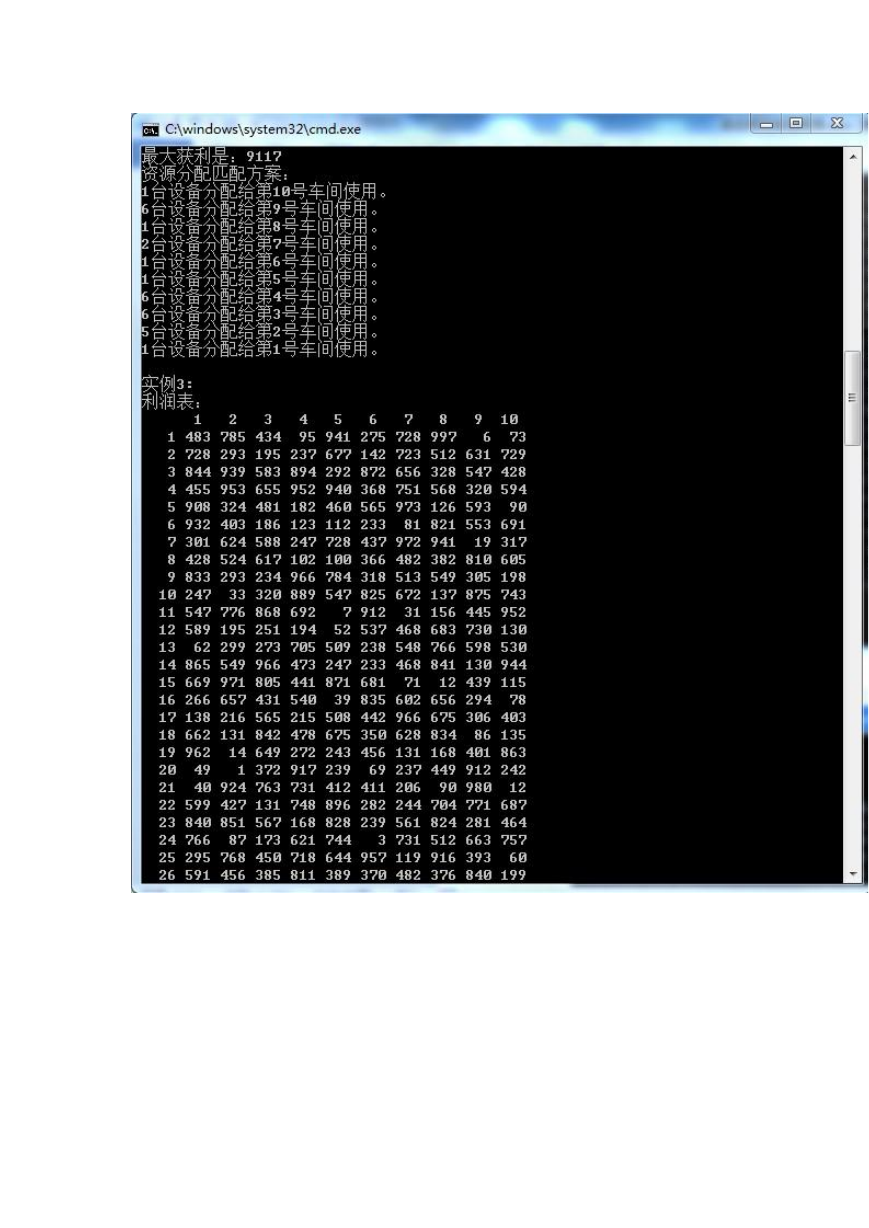









 2023年江西萍乡中考道德与法治真题及答案.doc
2023年江西萍乡中考道德与法治真题及答案.doc 2012年重庆南川中考生物真题及答案.doc
2012年重庆南川中考生物真题及答案.doc 2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc 2020年四川甘孜小升初语文真题及答案I卷.doc
2020年四川甘孜小升初语文真题及答案I卷.doc 2020年注册岩土工程师专业基础考试真题及答案.doc
2020年注册岩土工程师专业基础考试真题及答案.doc 2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc 2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc 2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc 2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc 2012年河北国家公务员申论考试真题及答案-省级.doc
2012年河北国家公务员申论考试真题及答案-省级.doc 2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc 2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc