2011年甘肃省嘉峪关市中考数学真题及答案.doc-资料库

第1页 / 共11页

第2页 / 共11页

第3页 / 共11页

第4页 / 共11页

第5页 / 共11页

第6页 / 共11页

第7页 / 共11页

第8页 / 共11页

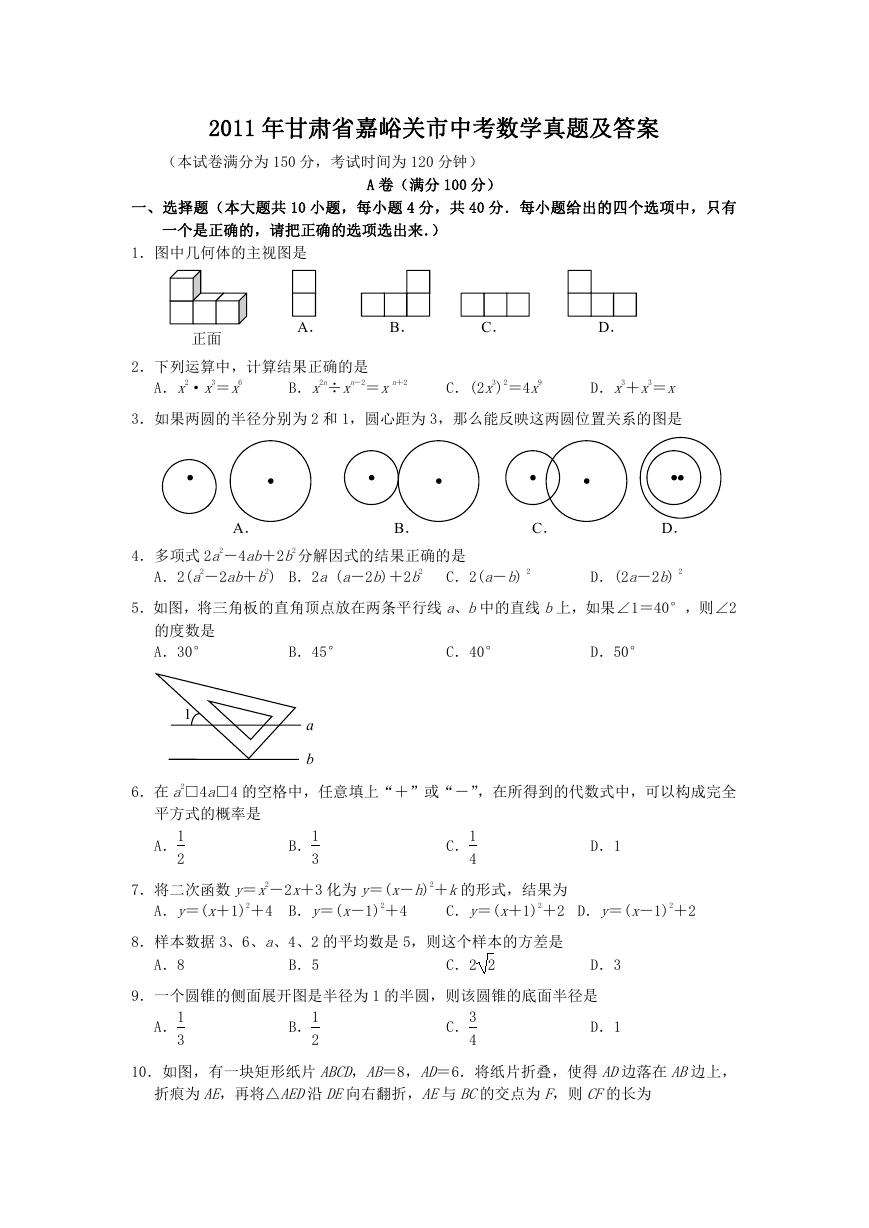
2011 年甘肃省嘉峪关市中考数学真题及答案（本试卷满分为 150 分，考试时间为 120 分钟） A 卷（满分 100 分）一、选择题（本大题共 10 小题，每小题 4 分，共 40 分．每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来．） 1．图中几何体的主视图是正面 A． B． C． D． 2．下列运算中，计算结果正确的是 A．x2·x3＝x6 B．x2n÷xn－2＝xn＋2 C．(2x3)2＝4x9 D．x3＋x3＝x 3．如果两圆的半径分别为 2 和 1，圆心距为 3，那么能反映这两圆位置关系的图是 A． B． C． D． 4．多项式 2a2－4ab＋2b2 分解因式的结果正确的是 A．2(a2－2ab＋b2) B．2a (a－2b)＋2b2 C．2(a－b) 2 D．(2a－2b) 2 5．如图，将三角板的直角顶点放在两条平行线 a、b中的直线 b上，如果∠1＝40°，则∠2 的度数是 A．30° 1 B．45° C．40° D．50° a b 6．在 a2□4a□4 的空格中，任意填上“＋”或“－”，在所得到的代数式中，可以构成完全平方式的概率是 1 A． 2 1 B． 3 1 C． 4 D．1 7．将二次函数 y＝x2－2x＋3 化为 y＝(x－h)2＋k的形式，结果为 A．y＝(x＋1)2＋4 B．y＝(x－1)2＋4 C．y＝(x＋1)2＋2 D．y＝(x－1)2＋2 8．样本数据 3、6、a、4、2 的平均数是 5，则这个样本的方差是 A．8 B．5 C．2 2 D．3 9．一个圆锥的侧面展开图是半径为 1 的半圆，则该圆锥的底面半径是 1 A． 3 1 B． 2 3 C． 4 D．1 10．如图，有一块矩形纸片 ABCD，AB＝8，AD＝6．将纸片折叠，使得 AD边落在 AB边上，折痕为 AE，再将△AED沿 DE向右翻折，AE与 BC的交点为 F，则 CF的长为

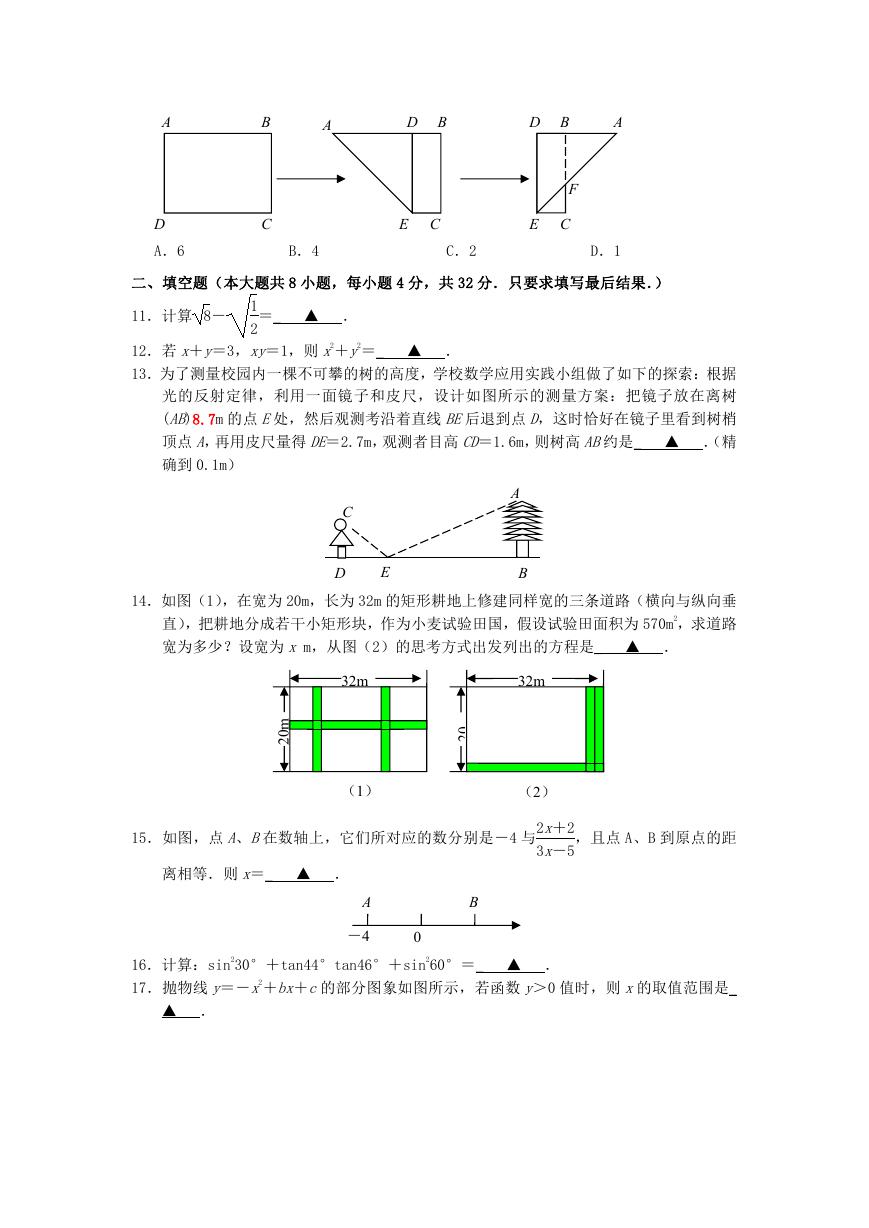
A D A．6 B C A D B D B A E C F E C B．4 C．2 D．1 二、填空题（本大题共 8 小题，每小题 4 分，共 32 分．只要求填写最后结果．） 11．计算 8－＝_ ▲ ． 1 2 12．若 x＋y＝3，xy＝1，则 x2＋y2＝_ ▲ ． 13．为了测量校园内一棵不可攀的树的高度，学校数学应用实践小组做了如下的探索：根据光的反射定律，利用一面镜子和皮尺，设计如图所示的测量方案：把镜子放在离树 (AB)8.7m 的点 E处，然后观测考沿着直线 BE后退到点 D，这时恰好在镜子里看到树梢顶点 A，再用皮尺量得 DE＝2.7m，观测者目高 CD＝1.6m，则树高 AB约是_ ▲ ．（精确到 0.1m） C D E A B 14．如图（1），在宽为 20m，长为 32m 的矩形耕地上修建同样宽的三条道路（横向与纵向垂直），把耕地分成若干小矩形块，作为小麦试验田国，假设试验田面积为 570m2，求道路宽为多少？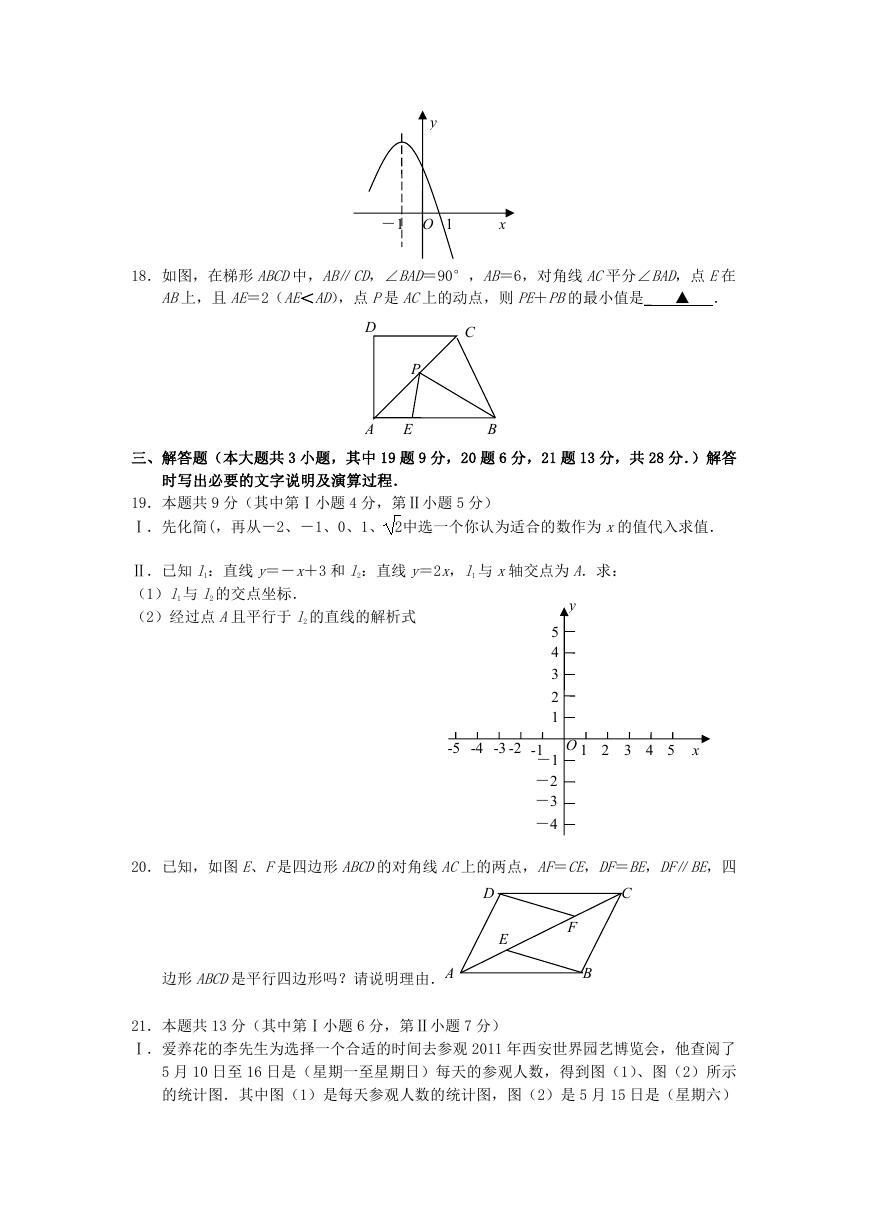设宽为 x m，从图（2）的思考方式出发列出的方程是_ ▲ ． 32m 32m m 0 2 0 2 （1）（2） 15．如图，点 A、B在数轴上，它们所对应的数分别是－4 与 2x＋2 3x－5 ，且点 A、B 到原点的距离相等．则 x＝_ ▲ ． A －4 0 B 16．计算：sin230°＋tan44°tan46°＋sin260°＝_ ▲ ． 17．抛物线 y＝－x2＋bx＋c的部分图象如图所示，若函数 y＞0 值时，则 x的取值范围是_ ▲ ．

y －1 O 1 x 18．如图，在梯形 ABCD中，AB∥CD，∠BAD＝90°，AB＝6，对角线 AC平分∠BAD，点 E在 AB上，且 AE＝2（AE＜AD），点 P是 AC上的动点，则 PE＋PB的最小值是_ ▲ ． D C P A E B 三、解答题（本大题共 3 小题，其中 19 题 9 分，20 题 6 分，21 题 13 分，共 28 分．）解答时写出必要的文字说明及演算过程． 19．本题共 9 分（其中第Ⅰ小题 4 分，第Ⅱ小题 5 分） Ⅰ．先化简(，再从－2、－1、0、1、 2中选一个你认为适合的数作为 x的值代入求值． Ⅱ．已知 l1：直线 y＝－x＋3 和 l2：直线 y＝2x，l1 与 x轴交点为 A．求：（1）l1 与 l2 的交点坐标．（2）经过点 A且平行于 l2 的直线的解析式 y 5 4 3 2 1 1 2 3 4 5 x -5 -4 -2-3 O y -1 －1 －2 －3 －4 20．已知，如图 E、F是四边形 ABCD的对角线 AC上的两点，AF＝CE，DF＝BE，DF∥BE，四边形 ABCD是平行四边形吗？请说明理由． A D E C F B 21．本题共 13 分（其中第Ⅰ小题 6 分，第Ⅱ小题 7 分） Ⅰ．爱养花的李先生为选择一个合适的时间去参观 2011 年西安世界园艺博览会，他查阅了 5 月 10 日至 16 日是（星期一至星期日）每天的参观人数，得到图（1）、图（2）所示的统计图．其中图（1）是每天参观人数的统计图，图（2）是 5 月 15 日是（星期六）

这一天上午、中午、下午和晚上四个时段参观人数的扇形统计图，请你根据统计图解答下面的问题：（1）5 月 10 日至 16 日这一周中，参观人数最多的是日是_ ▲ ，有_ ▲ 万人，参观人数最少的是日是_ ▲ ，有_ ▲ 万人，中位数是_ ▲ ．（2）5 月 15 日是（星期六）这一天，上午的参观人数比下午的参观人数多多少人？（精确到 1 万人）（3）如果李先生想尽可能选择参观人数较少的时间参观世园会，你认为选择什么时间较合适？ Ⅱ．如图在等腰 Rt△OBA和 Rt△BCD中，∠OBA＝∠BCD＝90°，点 A和点 C都在双曲线 y＝（k＞0）上，求点 D的坐标． 4 x y y＝4 x A C O B D x B 卷（满分 50 分）四、解答题（本大题共 50 分，解答时写出必要的演算步骤过程及推理过程．） 22．（8 分）如图，在平面直角坐标系中，O为坐标原点，每个小方格的边长为 1 个单位长度．正方形 ABCD顶点都在格点上，其中，点 A的坐标为 (1，1)．（1）若将正方形 ABCD绕点 A顺时针方向旋转，点 B到达点 B1，点 C到达点 C1，点 D到达点 D1，求点 B1、C1、D1 的坐标．（2）若线段 AC1 的长度．．与点 D1 的横坐标．．．的差．恰好是一元二次方程 x2＋ax＋1＝0 的一个根，求 a的值．

y C D O A B x 第 220 题 23．（10 分）某校开展的一次动漫设计大赛，杨帆同学运用了数学知识进行了富有创意的图案设计，如图（1），他在边长为 1 的正方形 ABCD内作等边△BCE，并与正方形的对角线交于点 F、G，制作如图（2）的图标，请我计算一下图案中阴影图形的面积． B A C D F G O E (1) A F G E (2) D 24．（10 分）某电脑公司各种品牌、型号的电脑价格如下表，育才中学要从甲、乙两种品牌电脑中各选择一种型号的电脑．（1）写出所有选购方案（利用树状图或列表方法表示）．如果各种选购方案被选中的可能性相同，那么 A型号电脑被选中的概率是多少？（2）该中学预计购买甲、乙两种品牌电脑共 36 台，其中甲品牌电脑只选了 A型号，学校规定购买费用不能高于 10 万元，又不低于 9.2 万元，问购买 A型号电脑可以是多少台？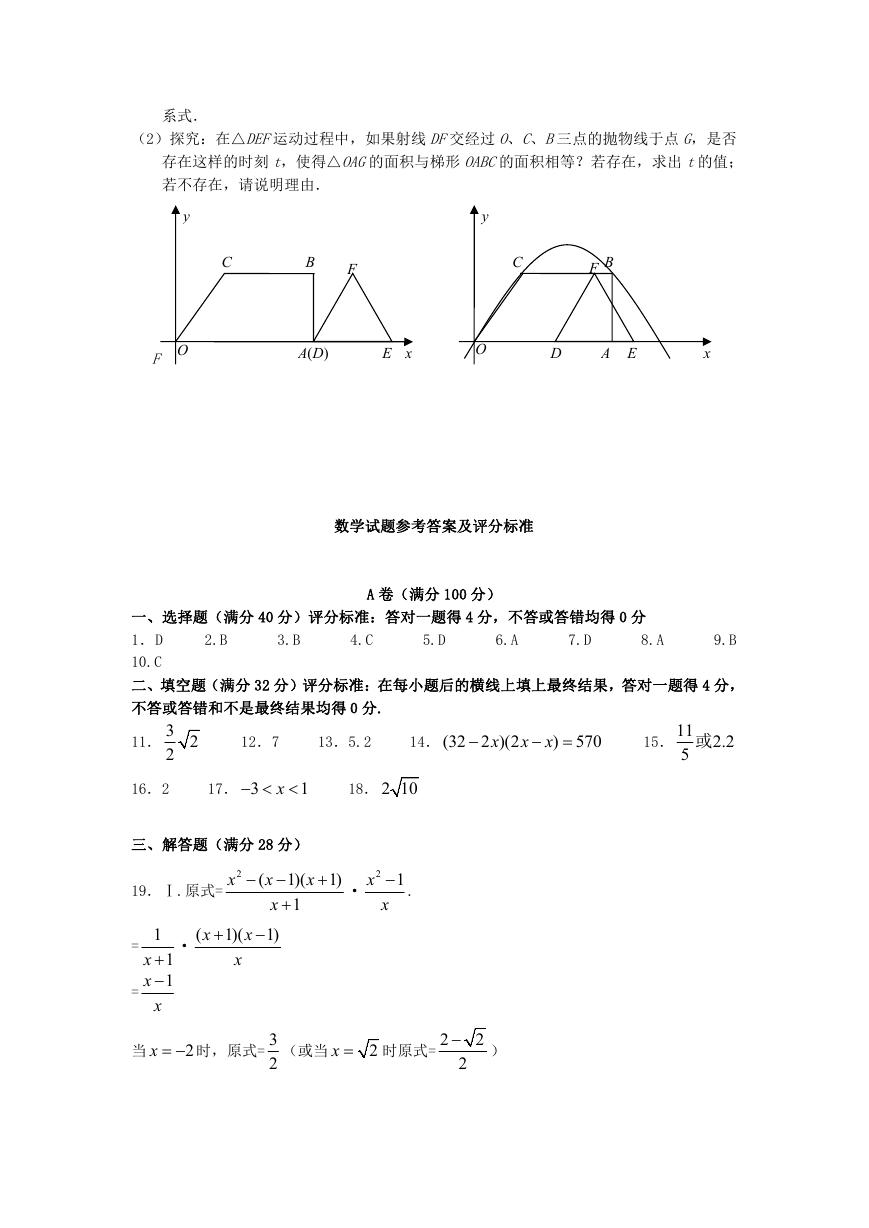型号 A 甲 B 乙 C D E 单价（元/台） 6000 4000 2500 5000 2000 25．（10 分）在△ABC中，AB＝AC，点 O是△ABC的外心，连接 AO并延长交 BC于 D，交△ABC 的外接圆于 E，过点 B作⊙O的切线交 AO的延长线于 Q，设 OQ＝，BQ＝3 2． 9 2 （1）求⊙O的半径；（2）若 DE＝ 3 5 ，求四边形 ACEB的周长． A B O E D C Q 26．（10 分）在梯形 OABC中，CB∥OA，∠AOC＝60°，∠OAB＝90°，OC＝2，BC＝4，以点 O 为原点，OA所在的直线为 x轴，建立平面直角坐标系，另有一边长为 2 的等边△DEF， DE在 x轴上（如图（1）），如果让△DEF以每秒 1 个单位的速度向左作匀速直线运动，开始时点 D与点 A重合，当点 D到达坐标原点时运动停止．（1）设△DEF运动时间为 t，△DEF与梯形 OABC重叠部分的面积为 S，求 S关于 t的函数关

系式．（2）探究：在△DEF运动过程中，如果射线 DF交经过 O、C、B三点的抛物线于点 G，是否存在这样的时刻 t，使得△OAG的面积与梯形 OABC的面积相等？若存在，求出 t的值；若不存在，请说明理由． y C B F O F A(D) E x y O C B F D A E x 数学试题参考答案及评分标准 A 卷（满分 100 分） 2.B 3.B 4.C 一、选择题（满分 40 分）评分标准：答对一题得 4 分，不答或答错均得 0 分 1．D 10.C 二、填空题（满分 32 分）评分标准：在每小题后的横线上填上最终结果，答对一题得 4 分，不答或答错和不是最终结果均得 0 分. 5.D 6.A 7.D 8.A 9.B 11． 3 2 2 12．7 13．5.2 14． (32 2 )(2  x x  x ) 570  15． 11 5 或 2.2 16．2 17． 3 1x    18． 2 10 三、解答题（满分 28 分） x  1) · x 2 1  x . 1)( x  1 x  1) 19．Ⅰ.原式= 2 x  ( ( x  · x  1)( x = = 1 1x  1x  x 当 x   时，原式= 2 3 2 （或当 x  时原式= 2 2 ） 2  2

Ⅱ.解：（1）设直线 1l 与 2l 的交点为 M ，则由    3 y    y x x 2 1, 2. 解得 x    y ∴ (1 2)M ， . (2)设经过点 A 且平行于 2l 的直线的解析式为 2  y . x b  ∵直线 1l 与 x 轴的交点 (3 0) A ， ∴ 6 则：所求直线的解析式为 2 x b  ，∴ b   6. 0 y  6.  ， 20.解：结论：四边形 ABCD 是平行四边形. 证明：∵ DF ∥ BE . ∴∠ AFD =∠CEB . 又∵ AF CE DF BE ， ∴△ AFD ≌△CEB （SAS）. ∴ AD CB ，∠ DAF =∠ BCE . ∴ AD ∥CB . ∴四边形 ABCD 是平行四边形. 说明：其它证法可参照上面的评分标准评分. 21.Ⅰ.①15，34；10，16；22 万； ②34(74%-6%)≈23（万人） ③答案不唯一，只要符合题意均可得分. Ⅱ．解：点 A 在双曲线 y ∴ AB OB  2  上，且在△OBA 中，AB OB 4 x ，∠ OBA  °则 90 OB AB   4 . 过点C 作CE ⊥ x 轴于 E CF， ⊥ y 轴于 F .设 BE x . 中由在 BCD△ 又点C 在双曲线  BC CD 4 x y  上，∠ BCD  90 °.则CE x . x x  ( 2)  4. 解得 x   5 1  ， x 0 ，

x   OD  5 1.  2 2( 5 1)     ， 2 5 点 (2 5,0) D ．四、解答题（本大题共 50 分，解答时写出必要的演算步骤及推理过程） B 卷（满分 50 分） B 22.解：（1）由已知 1 (2 (3 2) ，，，，， (4 0) 1) D 1 C 1 （2）由勾股定理得： AC  10 则 ( 10 3) 是方程 2 x ax 1 0   的一根，设另一根为 0x ，则 0x ( 10 3) =1. x  0 1 10 3   10 3  a   [( 10 3)   ( 10 3)]    2 10 a a 2    另解： ， 1 0   ( 10 3) ( 10 3) 2 10. 23.解：连接 FG 并延长交 AB 于 M AC，于 N ， △   MN AB MN CD  ， 45 ABE  ∠ ，∠ 和四边形 ABCD 分别是正三角形和正方形. BCE  BAC .  30   设 MF x ，则 x  3 x  1.   x  S 1 3 1  S =  3 1  2 阴影正方形  S △ BCE  2 S △ ABF . 1   1 4 3  3 1  2  6 3 3  4 另解： S 阴影    ( 1 1 3 4 2 2 6 3 3   4 1 4 1 2  S  S 正方形四边形 BCDF )(1 2   3 1  2 )

资料库

2011年甘肃省嘉峪关市中考数学真题及答案.doc

相关推荐

中考

热门标签

最新资料