用改进的欧拉方法和四阶龙格-库塔方法解初值问题 一、题目： 取步长 2.0h ，分别用改进的欧拉方法和四阶龙格—库塔方法解初值问题    ' x y  .1)0(   y y 0, ;1 x 并比较结果。 二、基本思想： 1.改进的欧拉方法 改进的欧拉方法用梯形公式计算  y x  +1 -  y x n n  = +1  x n x n   f x y x dx   , . 中的积分，并以 ny 和 +1ny 分别表示  y x 和  n +1n y x 的近似值，就得到 y n +1 = + y n  h 2  , f x y n n   + f x n , y +1 n +1   . （梯形公式） 梯形公式也是一个一步法公式。由于公式右端也含有未知的 +1ny ，故被称作是隐式的。 隐式格式实际上是关于 +1ny 的一个函数方程。为了避免解方程，可以采用欧拉方法计算初始 值，再由梯形公式计算。这样建立起来的计算格式称为改进的欧拉格式：     y p y n +1  n , = + , y hf x y n  , f x y = + y n n n  h  2   + f x n , y +1 n n +1   . 梯形公式也可以采用迭代法求解。如果仍然采用欧拉方法计算迭代初值，那么计算格式就是  n , = + , y hf x y n  , f x y n n n y y   0 +1 n   +1 k +1 n = + y      h  2  由于已假定  h 2   k +1 n = ,  f x n y - y   +1 k +1 n  从而，迭代的收敛条件是 0<   k +1 n y +1,  - f x n hL 2 <1. 2.四阶龙格-库塔方法  + f x n  n , y   k +1 n +1   . f x y 满足里普希兹条件，所以有  , y  -1 k +1 n +1   hL 2 y   k +1 n - y  -1 k +1 n  . 龙格—库塔方法不是用求导数的办法，而是用计算不同点上  yxf , 的函数值，然后对 这些函数值作线性拟合，构造近似公式。组合的原则是使得近似公式与泰勒展开式有尽 可能多的项吻合，以达到较高的精度。 改进的欧拉格式 

    y p y n +1  n , = + , y hf x y n  , f x y = + y n n n  h  2   + f x n , y +1 n n +1   . 可以改写为 y  1 n y n  1 2  K 1  K 2 , 其中 K K 1 2    xhf n  xhf n ,  , n y n  K 1 . y , 1  可见改进的欧拉格式可这样理解：首先计算 x , 和 n y n x 1,  n y n  K 1 两点的函数 值  xf , 和  n y xf n 1,  n y n  K 1 ，然后以它们的算术平均值作为  yxf , 的近似值，而 点 x n +1 , + y K 中的 1K 则是通过已知值 ny 来预报的。这个处理过程告诉我们：如果设 n 1  法多计算几个点处的函数值，然后以这些值得某种加权平均值作为  f x y 的近似值， , 则有可能构造出更精确的计算格式。 一般地龙格—库塔格式可以写成 N C K i , i i =1 y n +1 = + y n  , n 其中 K  1 , hf x y n  K hf = i    x a h y n , + + n i i -1  j =1 b K ij j    , =2,3, i , N  . 选择参数 , C a b 的原则是：要求 +1 n i y , ij i = + y n N C K i i =1 , i 的右端在 ,n x y 处的泰勒展开式按 h n  的幂重新排列后得到的 y n +1 = + y d h d h 2 n + 1 2 3 + d h  3 + 与微分方程的解  y x 在点 nx 的展开式 +1n  y x n +1   = y x n   + hy x ' n  + 又尽可能多的项重合。 1 2! '' 2 h y  x n  + 1 3! ''' 3 h y  x  n  + 经典的四阶龙格—库塔方法的计算公式是： 

y n +1 K 1  2 K 2  2 K 3  K 4  , 1 6 n  , hf x y n n              K 1 K 2 K 3 K 4   hf = + y         hf  , , + h y n , + h y n  1 2 1 2 x n + x n + K 1 K 2 , ,       1 2 1 2  .  + , + hf x h y K n n 3 三、程序设计： 1.改进的欧拉方法 eulerpro.m 文件 function [x,y]=eulerpro(h,x0,y0); x(1)=x0;y(1)=y0; for i=1:10; x(i+1)=x(i)+h; y1=y(i)+h*(x(i)+y(i)); y2=y(i)+h*(x(i+1)+y1); y(i+1)=(y1+y2)/2; end 计算：[x,y]=eulerpro(0.1,0,1) 2.四阶龙格-库塔方法 lgkt4j.m文件 function [x,y]=lgkt4j(x0,y0,h) x(1)=x0;y(1)=y0; for i=1:10 x(i+1)=x(i)+h; K1=h*(x(i)+y(i)); K2=h*(x(i)+1/2*h+y(i)+1/2*K1); K3=h*(x(i)+1/2*h+y(i)+1/2*K2); K4=h*(x(i)+h+y(i)+K3); y(i+1)=y(i)+1/6*(K1+2*K2+2*K3+K4); end 计算：[x,y]=lgkt4j(0,1,0.1) 四、结果分析： 改进的欧拉方法运行结果： x = 0 0.4000 0.8000 y = 1.0000 1.5818 2.6456 0.1000 0.5000 0.9000 1.1100 1.7949 3.0124 0.2000 0.6000 1.0000 1.2421 2.0409 3.4282 0.3000 0.7000 1.3985 2.3231 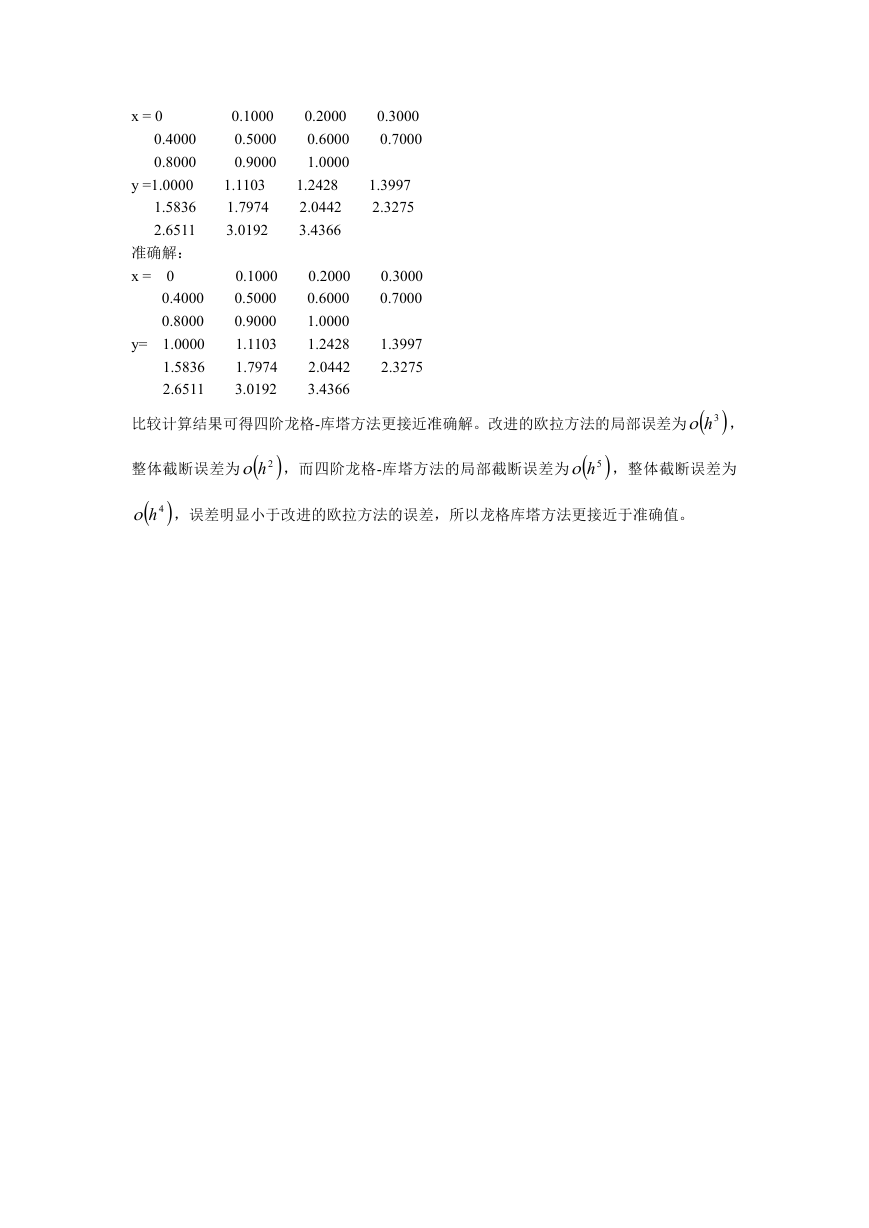四阶龙格-库塔方法运行结果： 

x = 0 0.4000 0.8000 y =1.0000 1.5836 2.6511 准确解： x = 0 0.4000 0.8000 y= 1.0000 1.5836 2.6511 0.1000 0.5000 0.9000 1.1103 1.7974 3.0192 0.2000 0.6000 1.0000 1.2428 2.0442 3.4366 0.3000 0.7000 1.3997 2.3275 0.1000 0.5000 0.9000 1.1103 1.7974 3.0192 0.2000 0.6000 1.0000 1.2428 2.0442 3.4366 0.3000 0.7000 1.3997 2.3275 比较计算结果可得四阶龙格-库塔方法更接近准确解。改进的欧拉方法的局部误差为  整体截断误差为   4h ，误差明显小于改进的欧拉方法的误差，所以龙格库塔方法更接近于准确值。 2h ，而四阶龙格-库塔方法的局部截断误差为  3h ， 5h ，整体截断误差为