第1页 / 共20页
第2页 / 共20页
第3页 / 共20页
第4页 / 共20页
第5页 / 共20页
第6页 / 共20页
第7页 / 共20页
第8页 / 共20页
生物医学信号处理习题.doc
第一章生物医学信号处理绪论
第二章数字信号处理基础
第三章随机信号基础
第四章数字卷积和数字相关
第五章维纳滤波
第六章卡尔曼滤波
第七章参数模型
第八章自适应信号处理
生物医学信号处理习题集
第一章 生物医学信号处理绪论...................................................................................................... 1
数字信号处理基础...............................................................................................................1
第二章
随机信号基础.......................................................................................................................5
第三章
第四章 数字卷积和数字相关.......................................................................................................... 9
第五章 维纳滤波.............................................................................................................................10
第六章 卡尔曼滤波.........................................................................................................................13
第七章 参数模型.............................................................................................................................16
自适应信号处理.................................................................................................................19
第八章
第一章 生物医学信号处理绪论
1. 生物医学信号处理的对象是什么信号？
解答：
包括生理过程自发产生的信号，如心电、脑电、肌电、眼电、胃电等电生理信号和血压、体温、脉
搏、呼吸等非电生理信号；还有外界施加于人体的被动信号，如超声波、同位素、X 射线等。
2. 生物信号的主要特点是什么？
解答：
随机性强，噪声背景强。
第二章 数字信号处理基础
You can use Matlab where you think it’s appropriate.
1.FIR 滤波器和 IIR 滤波器的主要区别是什么？
解答：
FIR 滤波器的单位脉冲响应是有限长的序列，该滤波器没有极点，具有稳定性。
IIR 滤波器的单位脉冲响应是无限长的序列，该滤波器有极点，有可能不稳定。
2.两个滤波器级联，第一个的传递函数为
1)z(H
1
-1
2z
2
z
，第二个为
z1)z(H
2
-1
，当输入为单
位脉冲时，求输出序列，画出级联滤波器的频率响应。
解答：
)z(H
1(
2z
-1
z
2
1
)z1)(
=
z1
-1
z
2
z
3
h(n)=[1,1,-1,-1]，n=0，1，2，3。即输入单位脉冲时的输出序列值。
freqz(h,1)
.0)2n(
0181x
)3n(
0.0181];
0.0543, 0.0543,
.0)1n(
2781y
0543x
)3n(
.0)n(
1829y
0543x
.0)2n(
.0
0181x
76y
.1)1n(
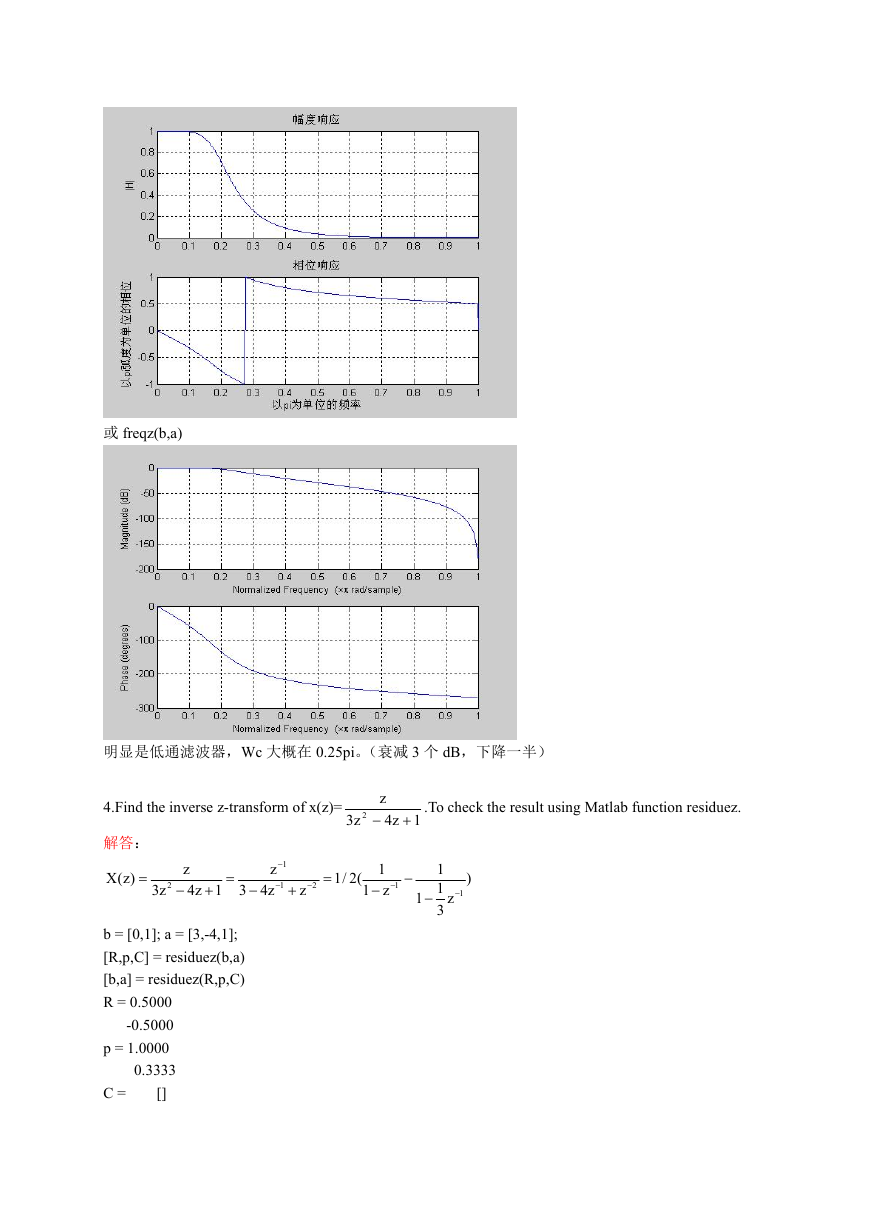
3.A 3rd-order lowpass filter is described by the difference equation:
)n(y
.1
Plot the magnitude and the phase response of this filter and verify that it is a lowpass filter.
解答：
b = [0.0181,
a = [1.0000, -1.7600, 1.1829, -0.2781];
m = 0:length(b)-1; l = 0:length(a)-1;
K = 500; k = 1:1:K;
w = pi*k/K; % [0, pi] 分成 501 个点.
num = b * exp(-j*m'*w); % 分子计算
den = a * exp(-j*l'*w); % 分母计算
H = num ./ den;
magH = abs(H); angH = angle(H);
subplot(1,1,1);
subplot(2,1,1); plot(w/pi,magH); grid; axis([0,1,0,1])
xlabel(''); ylabel('|H|');
title('幅度响应');
subplot(2,1,2); plot(w/pi,angH/pi); grid on; axis([0,1,-1,1])
xlabel('以 pi 为单位的频率'); ylabel('以 pi 弧度为单位的相位');
title('相位响应');
或 freqz(b,a)
明显是低通滤波器，Wc 大概在 0.25pi。（衰减 3 个 dB，下降一半）
4.Find the inverse z-transform of x(z)=
z
4z
1
2
3z
.To check the result using Matlab function residuez.
1
z
1
4z
(2/1
1
z1
1
2
z
1
11
3
)
1
z
解答：
)z(X
z
4z
2
3z
1
3
b = [0,1]; a = [3,-4,1];
[R,p,C] = residuez(b,a)
[b,a] = residuez(R,p,C)
R = 0.5000
-0.5000
p = 1.0000
0.3333
[]
C =
b = -0.0000
a = 1.0000
笔算和程序结果一致。
0.3333
-1.3333
0.3333
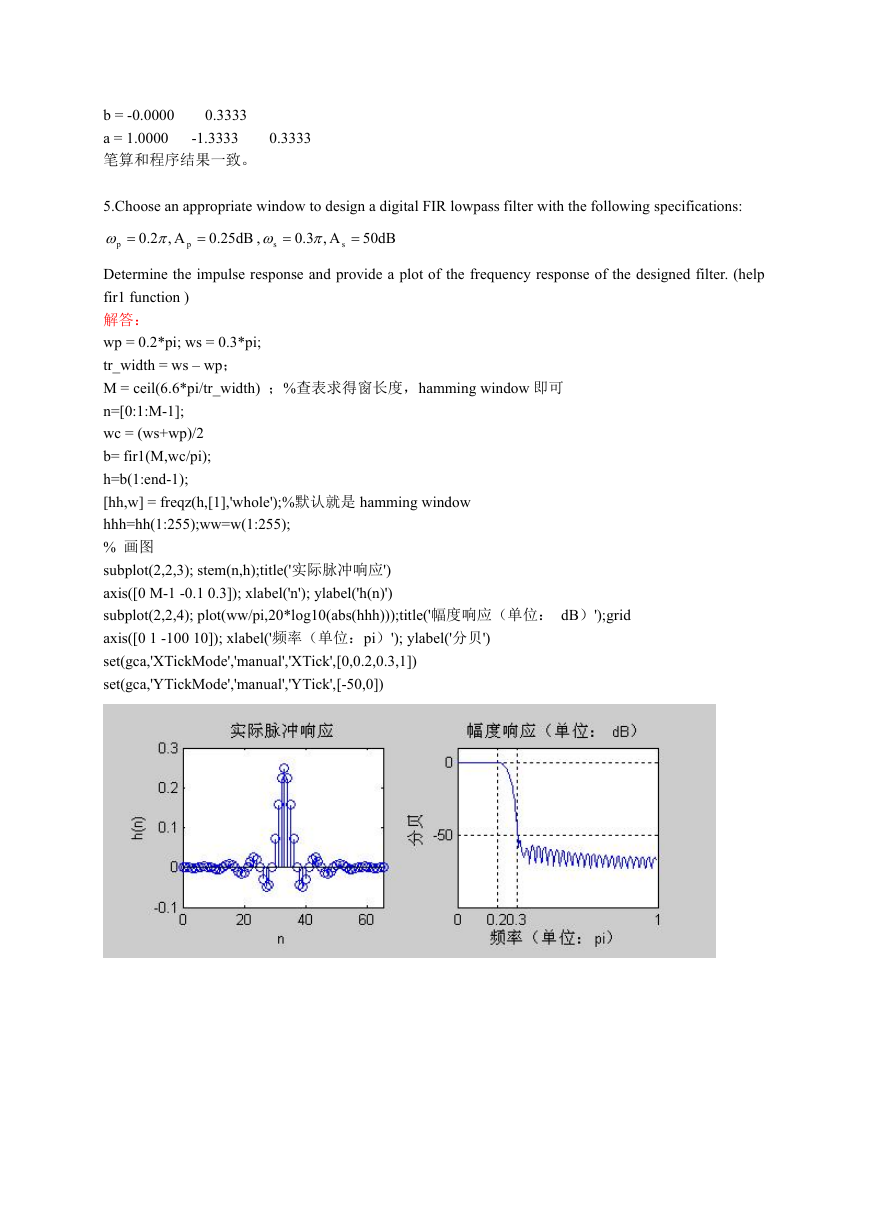
5.Choose an appropriate window to design a digital FIR lowpass filter with the following specifications:
p
A,2.0
p
.0
25dB
,
s
A,3.0
s
50dB
Determine the impulse response and provide a plot of the frequency response of the designed filter. (help
fir1 function )
解答：
wp = 0.2*pi; ws = 0.3*pi;
tr_width = ws – wp；
M = ceil(6.6*pi/tr_width) ；%查表求得窗长度，hamming window 即可
n=[0:1:M-1];
wc = (ws+wp)/2
b= fir1(M,wc/pi);
h=b(1:end-1);
[hh,w] = freqz(h,[1],'whole');%默认就是 hamming window
hhh=hh(1:255);ww=w(1:255);
% 画图
subplot(2,2,3); stem(n,h);title('实际脉冲响应')
axis([0 M-1 -0.1 0.3]); xlabel('n'); ylabel('h(n)')
subplot(2,2,4); plot(ww/pi,20*log10(abs(hhh)));title('幅度响应（单位： dB）');grid
axis([0 1 -100 10]); xlabel('频率（单位：pi）'); ylabel('分贝')
set(gca,'XTickMode','manual','XTick',[0,0.2,0.3,1])
set(gca,'YTickMode','manual','YTick',[-50,0])
第三章 随机信号基础
1.什么是平稳各态遍历的随机过程？
解答：
如果随机信号的统计特性与开始进行统计分析的时刻无关，则为平稳随机过程，否则为非平稳随机
过程。对于平稳过程，如果所有样本在固定时刻的统计特征和单一样本在全时间上的统计特征一致，
则为各态遍历的随机过程。平稳且各态遍历是本课程分析医学信号的一个前提假设
2.判断随机相位正弦波在均值意义下是否各态遍历。
)(
tx
A
sin(
)
0
t
，A 0 是固定值，是随
机变量，分布为均匀分布：
p
)(
1
2
0,
2
，其它为零。
解答：
该随机过程的时间平均为：
m
x
lim
T
1
2T
T
(Asin
T
t
dt)
0
0
该随机过程的总体平均为：
)x(E
A
A-
dx)x(xp
因此该过程在均值意义下是各态遍历的。
2
(Asin
0
d)(p)
t
0
0
3.讨论相互独立、互不相关、相互正交的区别和联系。
解答：
随机变量统计独立的条件为：
)y,x(
cov
互不相关的条件为：
)xy(E
0
正交的条件为：
)y,x(p
0
)y(p)x(p
对于一般的随机变量：统计独立则互不相关；当其中有任意一个变量的均值为零，则互不相关和正
交可以互相推导。
对于高斯随机变量，统计独立和互不相关可以相互推导；当其中有任意一个变量的均值为零，则三
者都能互相推导。
4.输入序列 nx 的一阶概率密度函数是
(
xp
n
)
2
e
2
x
n
(
xu
n
)
1x 、 2x 都是具有上述分布的随机序列，求
)(yE 。
解答：
)x(E
n
dx)x(px
n
n
n
0
x
n
2e
-2x
n
dx
n
0
x-
de
n
-2x
n
。证明：
(
nxE
)
5.0
y
2
x
1
4
x
2
，
；如
ex
n
2x
n
0
0
2x-
n
e
dx
n
0
2x- dx
e n
n
5.0
0
2x-
n
de
=
e(5.0
n2x
)
0
=0.5
E（y）=E(2x1+4x2)=E(2x1)+E(4x2)=3
5.已知平稳随机过程 x 的自相关函数如下，求其功率谱密度及均方，并根据所得结果说明该随机过
程是否含有直流分量或周期性分量。
（ⅰ）
)(R x
4e
cos
cos3
（ⅱ）
)(R
x
25e
4
解答：
cos
0
16
（ⅰ）
(P
x
)
e)(R
x
j
d
)]3
)3
([
(
[8
1
)
(1
2
1
)
(1
]
2
2
)0(R)x(E
x
因为
[8)0(P
x
514
2
2
1
0]
，所以含有直流分量；
因为周期信号的自相关函数也是周期性的，而 R 中包含有一个周期性的成分，因此该随机过程含有
周期性分量。
（ⅱ）
(P
x
)
e)(R
x
j
d
32
)
(
[50
16
1
(
0
2
)
1
(
0
]
2
)
16
2
)0(R)x(E
x
25
16
41
因为
)0(P
x
32
[50
2
0
2
16
0]
，所以含有直流分量；
因为周期信号的自相关函数也是周期性的，而 R 中没有包含周期性的成分，因此该随机过程不含有
周期性分量。
6.设 x（t）是平稳过程，
，证明的 )t(y 功率谱是：
)Tt(x)t(x
)t(y
(P
y
)
解答：
(P
y
)
e)(R
y
j
d
(2P
x
1)(
cos
)T
其中
t(y)t(y(E)(R y
))
))Tt(x)t(x[(E
t(x(
t(x)
))]T
t(x)t(x[E
t(x)Tt(x)
t(x)t(x)
t(x)Tt(x)T
)]T
(R)(R
x
x
(R)T
x
)(R)T
x
(P
y
)
e)(R
y
j
d
[2R
x
(R)(
x
(R)T
x
e)]T
j
d
(2Px
)
[R
x
(
(R)T
x
e)]T
j
d
(2P
x
e1)[
Tj
Tj
e
]
(2Px
1)(
cos
)T
，得证。
7. 一 个 随 机 信 号 )t(x1 的 自 相 关 函 数 是
eA)(R
1
1
， 另 一 个 随 机 信 号
)t(x 2 的 自 相 关 函 数 为
eA)(R
2
2
，在下列条件下，分别求信号相加后
x(t)
)t(x)t(x
1
2
的自相关函数
)(R x 。
（ⅰ） )t(x1 ， )t(x 2 相互独立；
（ⅱ） )t(x1 ， )t(x 2 来自同一信号源，只是幅度差一个常数因子 K（K 不为 1）： )t(x 2
=K
)t(x1 。
解答：
（ⅰ） )t(x1 ， )t(x 2 相互独立
t(x)t(x(E)(R x
))
))t(x)t(x[(E
2
1
t(x(
1
t(x)
2
))]
t(x)t(x[E
t(x)t(x)
t(x)t(x)
t(x)t(x)
)]
2
1
1
2
1
1
2
2
t(x[E)]t(x[E)(R
2
1
1
)]
t(x[E
1
)(R)]t(x[E)]
2
2
limR1
)(
limE[x
(t)x
1
1
(t
)]
t(x(E))t(x(E
1
1
))
2
)]t(x[E
1
2
)]t(x[E
1
0
，同理
2
)]t(x[E
2
0
)(R)(R)(R
2
1
x
)eAA(
2
1
（ⅱ） )t(x 2
=K
)t(x1
由前面计算可得
)(R x
t(x)t(x[E)(R
2
1
1
)]
t(x[E
1
)(R)]t(x)
2
2
t(Kx)t(x[E)(R
1
1
1
)]
t(x[E
1
)(R)]t(Kx)
2
1
)(R
1
2KR
1
)(R)(
2
8.
1
1
2KA
)eA
A(
nx 是零均值，方差为 2
2
x 的白噪过程，把它先送入一个平均器，得
y
n
1
2
(
x
n
1
n
x
)
，然后再将 ny 送
给一个差分器
z
n
y
n
1y
n
，求 nz 的均值、方差、自相关函数和功率谱密度。
解答：
1
2
(
x
n
x
n
1
)
1
2
x(
1-n
x
2n
)
1
2
(
x
n
2
n
x
)
n
n
z
y
1y
n
1(E)z(E
2
n
x(
x
n
2n
))
0
2
z
)z(E 2
n
2
)z(E
n
1[E
4
(
x
n
2
n
x
2
])
1[E
4
(
x
2
n
x2x
n
2n
2
x
2
n
)]
= 2
x /2=
)0(R nz
)1(R nz
=
zz(E
n
1n
)
(
x
n
x
n
2
x)(
1n
x
1n
)]
=0
=
zz(E
n
)2(R nz
当|m|>=3，自相关都为 0。
2n
x
)
(
n
x
n
2
x)(
2n
)]x
n
=－ 2
x /4
1[E
4
1[E
4
)m(R nz
=
)m([
1 2
x
2
1
2
11[
2
1
2
)2m(
1
2
)]2m(
1
2
1 2
2
-
e
jw2
2
x
)w(P nz
9. 随 机 序 列 nx 各 次 采 样 互 相 独 立 ， 且 均 匀 分 布 于 － 1 ～ 1 之 间 ， 设
cos2w
1[
x
jw2
e
]
]
y
n
x
n
1
n
x
，
z
n
x
n
2
x
1
n
x
n
2
，
w
n
5.0
w
n
1
x
n
，求 nx 的均值和方差； ny 、 nz 、 nw 的自相关函数和
功率谱。
解答：
均值：
)x(E
n
dx)x(px
n
n
n
=
1
x
1
n
0.5dx
n
0
均方值：
2
)x(E
n
2
dx)x(px
n
n
n
x1
1
2
n
0.5dx
n
1
3
方差：Var(xn)=
)x(E)x(E
n
2
n
2
)0(R ny
(E)y(E
2
n
x
n
x
1
n
)
2
=
1
3
2
3
yy(E)1(R
n
yn
)
x(E[
n
x
1n
1n
x)(
1n
)]x
n
1
3
yy(E)2(R
n
yn
)
x(E[
n
x
1n
x)(
2n
x
1n
2n
)]
0
，当|m|>=2 时，y 的自相关函数都为零
)m(R ny
=
1
3
)m(2[
)1m(
)]1m(
，
)w(P ny
2
3
11[
2
e
jw-
1
2
jw
]e
2
1[
3
cosw
]
。
)0(R nz
(E)z(E
2
n
x
n
2
x
1
n
x
2n
2
)
= 2
zz(E)1(R
n
zn
)
x(E[
n
2x
1n
1n
x
2n
x)(
1n
2x
n
x
1n
)]
zz(E)2(R
n
zn
)
x(E[
n
2x
1n
x
2n
x)(
2n
2x
1n
)]x
n
2n
当|m|>=3 时，z 的自相关函数都为零
)m(R nz
=
)w(P nz
1
3
1
3
)1m(4)1m(4)m(6[
)2m(
)]2m(
6[
4e
jw-
4e
jw
e
2jw
j2w
e
]
82
3
cosw
cos2w
4
3
1
3
，
，
。
2
3
1
4
)0(R nw
(E)w(E
2
n
5w.0
2
)
=
n
1
)wx(E)x(E
1n
2
n
n
2
)w(E
1n
，由于中间一项为零，所以有
)0(R nw
=
4
3
n =
2
)x(E
nx
4 ，
9
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
