第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
分治法求最近点对问题.docx
一、实验目的：
二、内容：
三、算法思想提示
四、实验要求
五、实验步骤、结果与分析
1.蛮力法：
2.分治法：
3.蛮力法与分治法算法效率比较：
六．实验心得
深 圳 大 学 实 验 报 告
课程名称：
算法设计与分析
实验名称：
分治法求最近点对问题
学院： 计算机与软件学院 专业： 计算机科学与技术
报告人： 学号：
班级：
同组人：
无
指导教师：
实验时间：
2017/10/12——2017/10/26
实验报告提交时间：
2017/10/26
教务处制
一、实验目的：
（1）掌握分治法思想。
（2）学会最近点对问题求解方法。
二、内容：
1. 对于平面上给定的N个点，给出所有点对的最短距离，即，输入是平面上的N个点，输出
是N点中具有最短距离的两点。
2. 要求随机生成N个点的平面坐标，应用蛮力法编程计算出所有点对的最短距离。
3. 要求随机生成N个点的平面坐标，应用分治法编程计算出所有点对的最短距离。
4. 分别对N=100,1000,10000,100000，统计算法运行时间，比较理论效率与实测效率的差异，
同时对蛮力法和分治法的算法效率进行分析和比较。
5. 如果能将算法执行过程利用图形界面输出，可获加分。
三、算法思想提示
1. 预处理：根据输入点集S中的x轴和y轴坐标进行排序，得到X和Y,很显然此时X和Y中的点
就是S中的点。
2. 点数较少时的情形
3. 点数|S|>3时，将平面点集S分割成为大小大致相等的两个子集SL和SR，选取一个垂直线L
作为分割直线，考虑XL和XR，YL和YR，这里还需要排序吗？
4. 两个递归调用，分别求出SL和SR中的最短距离为dl和dr。
5. 取d=min(dl, dr)，在直线L两边分别扩展d，得到边界区域Y，Y’是区域Y中的点按照y坐标
值排序后得到的点集，Y'又可分为左右两个集合Y’L和Y’R
6. 对于Y’L中的每一点，检查Y’R中的点与它的距离，更新所获得的最近距离
四、实验要求
1. 在blackboard提交电子版实验报告，注意实验报告的书写，整体排版。
2. 实验报告的实验步骤部分需详细给出算法思想与实现代码之间的关系解释，不可直接粘
贴代码（直接粘贴代码者视为该部分内容缺失）。
3. 实验报告样式可从http://192.168.2.3/guide.aspx 表格下载－学生适用－在校生管理－实
践教学－实验：深圳大学学生实验报告）
4. 源代码作为实验报告附件上传。
5. 在实验课需要现场运行验证。
五、实验步骤、结果与分析
1.蛮力法：
过程：（注：距离为 0 时不计入，即两点重合）
从 n 个点中选取第 i 个点，让其与余下（n-i）个点分别配对算出两点间距离，更新最短距离；
继续循环…….一直循环 n*(n-1)/2 次
实验结果：
以 n 个点为输入规模，固定 n，随机生成并运行 20 组测试样本，统计出蛮力法在 20 个随机
样本上的平均运行时间（ms）。（n=100,1000,10000,100000）
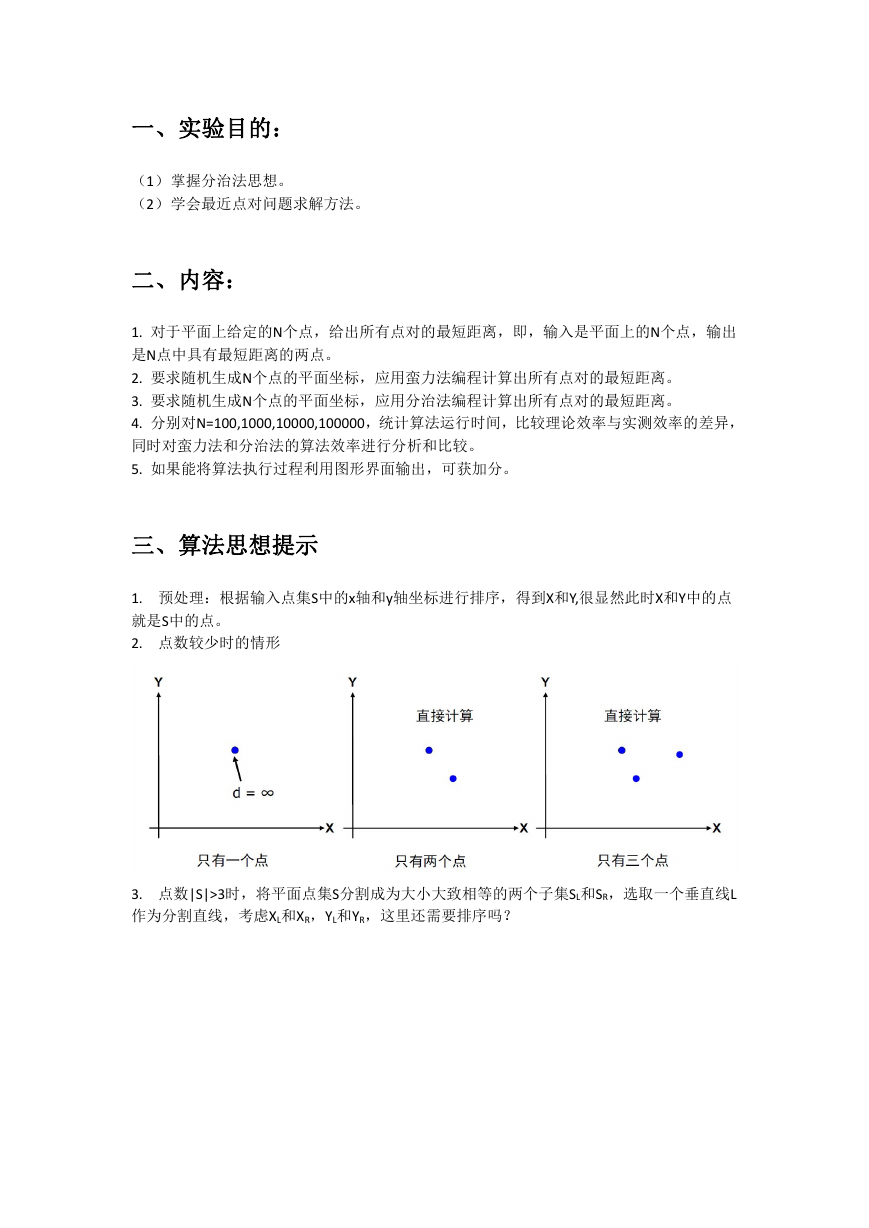
作出在蛮力法下 20 个随机样本的平均运行时间与输入规模 n 的关系图如下：
性能分析：
从数学角度看，n 个点间两两配对可以形成 n*（n-1）/2 对点对，算出他们之间的距离，再
从中筛选出最短距离。详细求解如下：
T(n)=(n-1)+(n-2)+…+2+1+0=(n-1+0)*n/2=1/2*n^2-1/2*n
所以蛮力法的时间复杂度为：
O(n^2)
作出在蛮力法下比较操作执行次数与输入规模 n 的关系图如下：
结论：
以输入规模为 1000 的数据运行时间为基准点，计算输入规模为其他值的理论运行时间，画
出不同规模数据的理论运行时间与实际运行时间曲线的对比图如下：
通过分析对比在蛮力法下理论与实际时间效率可知，二者极为相近，蛮力法时间复杂度为
O(n^2)。
2.分治法：
过程：（注：距离为 0 时不计入，即两点重合）
a. 递归停止条件。当点集 p 里只有一个点或没有点时，无距离；当点集 p 里只有两个点时，
直接计算两点间距离；当点集 p 里有三个点时，调用蛮力法求出三点间最短距离。
b. 将点集 p 里的点投影到平面坐标轴 x-y 上，以直线 x=L（x 轴上的中线）将点集 p 划分为
两个集合：SL（xL）。
c. 两个递归调用，分别求出 SL 和 SR 中的最短距离为 dl 和 dr。
d. 取 d=min(dl,dr)，获取边界区域 Y（[L-d,L+d]），并将其划分为两个集合 yl（[L-d,L]）和 yl
（[L,L+d]）。
e. 对于 yl 中的每一点，检查 yr 中的点与它的距离，并更新所获得的最近距离。
f. 最终结果筛选。因为划分 yl 和 yr 时，将在分割线 x=L 上的点重复划分到了两个集合中，
所以需要对所获得的最近点对进行筛选，排除重复计入的点对。
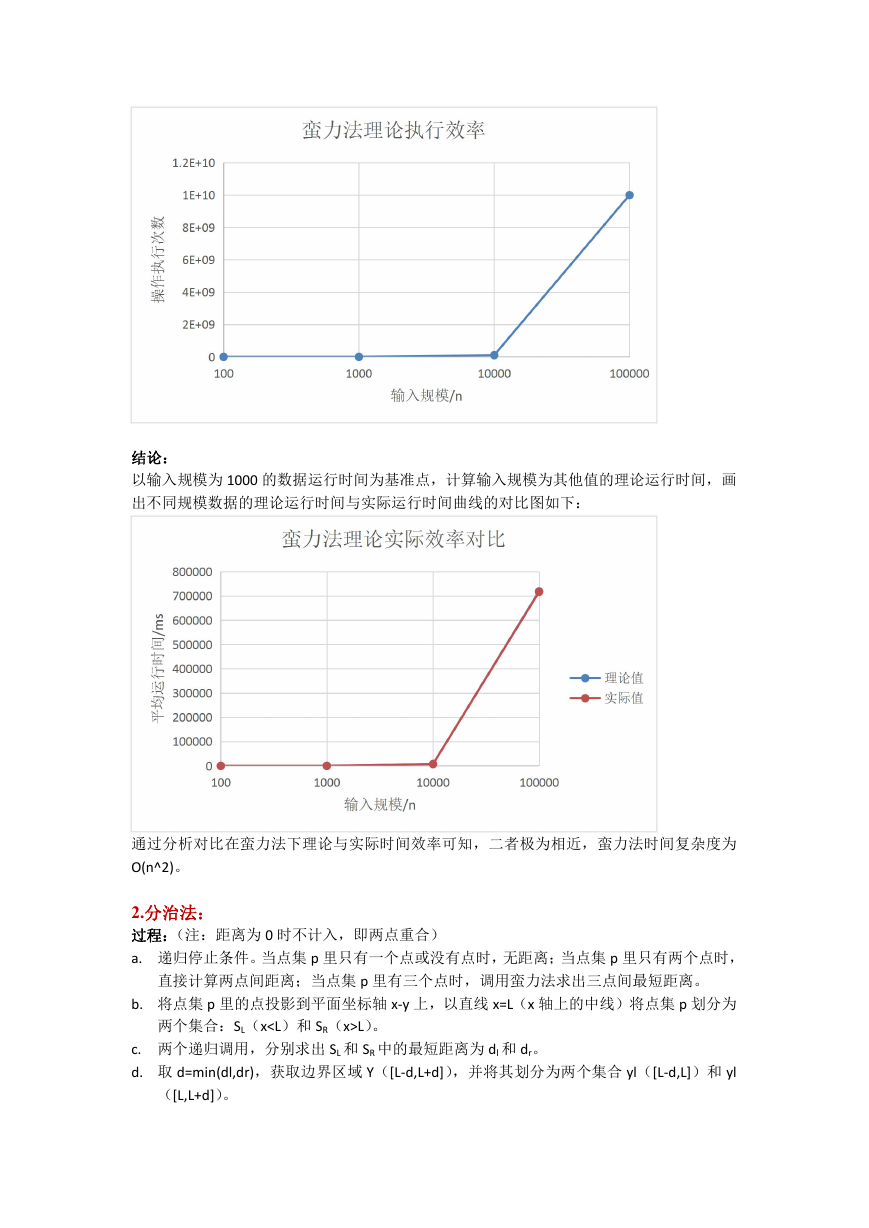
实验结果：
以 n 个点为输入规模，固定 n，随机生成并运行 20 组测试样本，统计出分治法在 20 个随机
样本上的平均运行时间（ms）。（n=100,1000,10000,100000）
作出在分治法下 20 个随机样本的平均运行时间与输入规模 n 的关系图如下：
性能分析：
运用主定理法分析最近点对分治算法如下：
T(n) = 2T(n/2) + 3*n
a=2,b=2,d=1
因为 a=bd，所以 T(n)属于 O(ndlogn)，故分治算法的时间复杂度为：
O(nlogn)
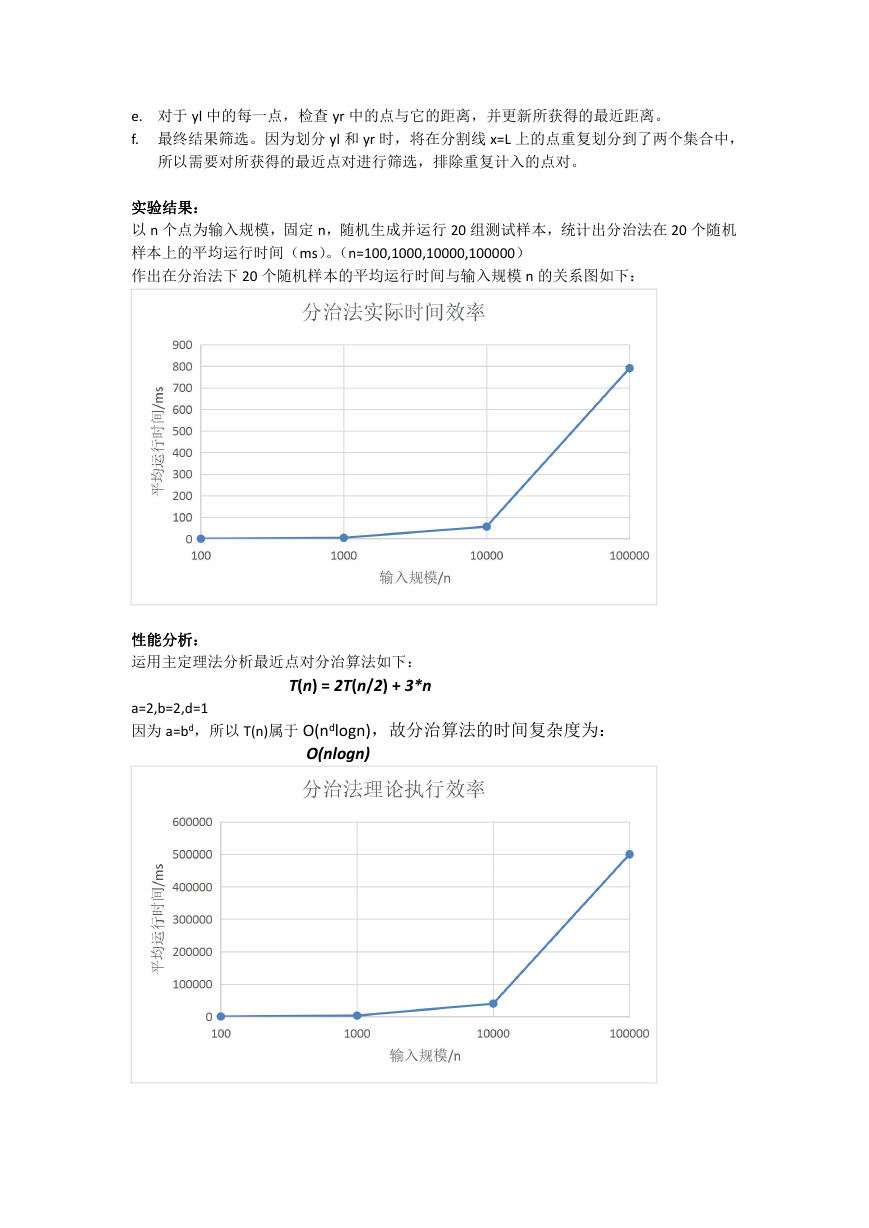
结论：
以输入规模为 1000 的数据运行时间为基准点，计算输入规模为其他值的理论运行时间，画
出不同规模数据的理论运行时间与实际运行时间曲线的对比图如下：
通过分析对比在分治法下的时间效率，可知实际效率与理论效率大致吻合，时间复杂度计算
值正确。
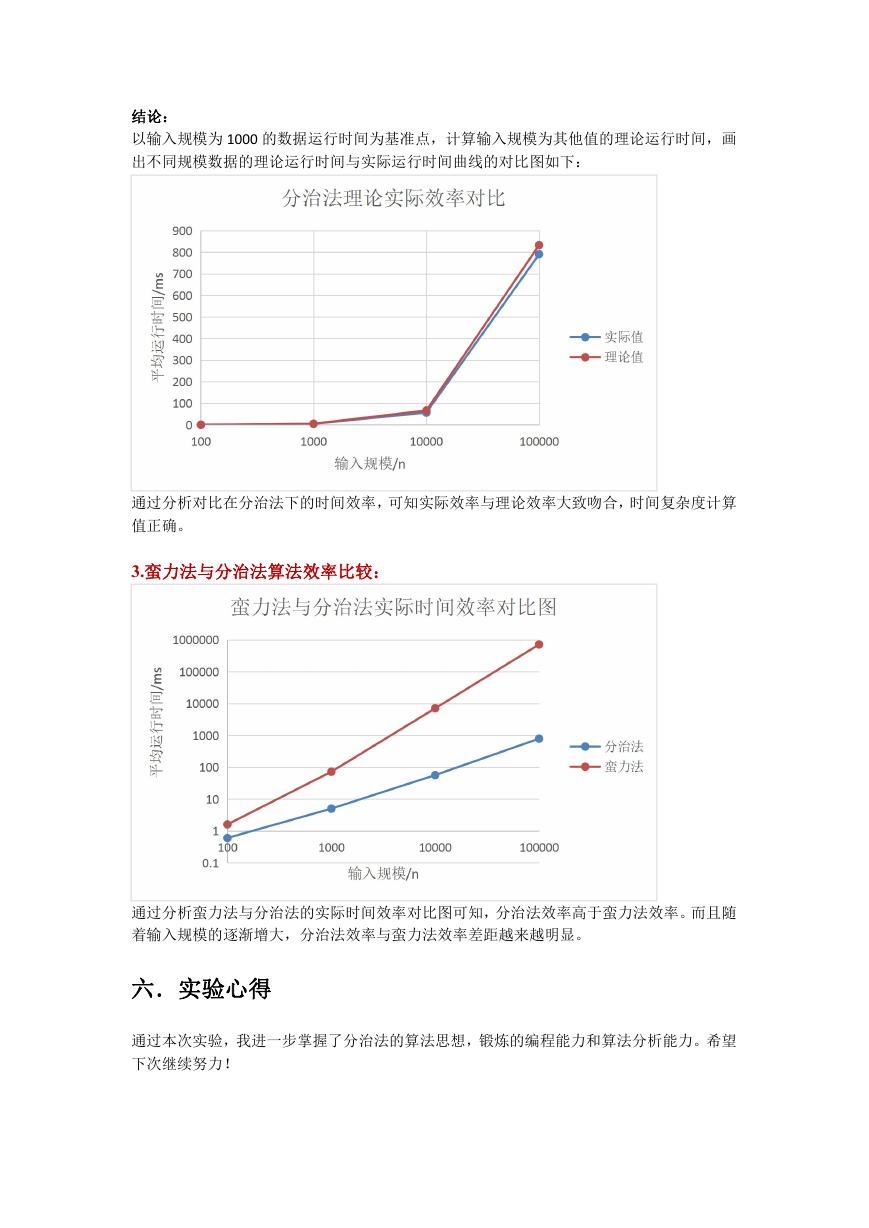
3.蛮力法与分治法算法效率比较：
通过分析蛮力法与分治法的实际时间效率对比图可知，分治法效率高于蛮力法效率。而且随
着输入规模的逐渐增大，分治法效率与蛮力法效率差距越来越明显。
六．实验心得
通过本次实验，我进一步掌握了分治法的算法思想，锻炼的编程能力和算法分析能力。希望
下次继续努力！
指导教师批阅意见：
成绩评定：
备注：
指导教师签字：
年
月
日
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
