中国科技论文在线 http://www.paper.edu.cn 煤炭需求预测模型分析 蔡武 1，袁莎莎 2，张强 1 1 中国矿业大学矿业工程学院，江苏徐州，221116 2 中国矿业大学计算机科学与技术学院，江苏徐州，221116 E-mail：aaacaiwu@126.com 摘 要：基于回归曲线拟合，灰色预测和最优组合模型，建立了全国煤炭需求量的预测模型， 并利用各模型预测了全国 2009 年的煤炭需求量。最后，对三种模型的预测结果作了分析， 得出结论：最优组合预测模型从总体上起到了提高预测精度的作用，用此方法进行预测是有 效的，预测的结果是可信的。 关键词：煤炭需求；回归曲线拟合；灰色预测；最优组合预测 0 前言 2004年通过的《能源中长期发展规划纲要(2004年-2020年)》中明确规定：实施“以煤为 主体，电力为中心，油气和新能源全面发展的战略”。建国以来，煤炭在我国一次能源消费 构成中占75%左右，预计到2050年，这一比例仍将高达50%以上。表1[1]为近年我国煤炭消费 总量和GDP总量及其增长率，图1表示出了煤炭消费量增长率和GDP增长变化趋势。 年 份 煤炭消费量（亿吨） 1999 2000 2001 13.2 12.9 13.4 煤炭消费量增长率（%） — 2.33 1.52 8.95 8.21 9.73 — 9.01 8.72 表1 近年我国煤炭消费总量和GDP总量及其增长率 2005 21.7 12.44 18.2 13.75 GDP（万亿元） GDP 增长率（%） 2004 19.3 14.88 16 36.75 2003 16.8 19.15 11.7 12.50 2002 14.1 5.22 10.4 6.89 2007 2006 25.23 23.8 6.01 9.68 20.9 24.7 14.84 18.18 2008 27.4 8.60 30.1 21.86 从图1可以看出，煤炭消费量的变化同GDP的变化具有很好的一致性，这一点充分说明 了煤炭的需求量与国民经济的增长息息相关。因此，及时了解煤炭需求量的变化，尤其是近 期的变化趋势，可以及时地掌握决策的主动权，做出合理的决策。同时，保障我国煤炭供应 安全对能源安全具有重要作用，而不断提高煤炭需求量预测精度对保障我国煤炭供应安全具 有重要意义。 图1 煤炭消费量增长率和GDP增长变化趋势 本文根据煤炭消费的时间序列特点，建立了回归曲线拟合模型和灰色预测模型，为了提 高预测精度，减少由单一模型求解的系统误差，建立了回归曲线拟合模型与灰色预测模型的 优化组合模型，预测全国2009年的煤炭需求。 1 回归曲线拟合模型 回归分析的原理是最小二乘原理。最小二乘原理就是找到一条曲线 ˆy ，使散点 ( x y 的 i ) , i iy 值 与 曲 线 ˆy 的 ˆiy 值 之 差 趋 于 最 小 。 给 定 函 数 x y n ( , ) , i i ky x k ⋅⋅⋅ ，选取一组简单函数 ( )( 0,1, 0,1, i )( m = = ) , 的 一 组 观 测 值 ⋅⋅⋅ 作为基函数，建立拟合模型 y = f x ( ) - 1 - 

中国科技论文在线 http://www.paper.edu.cn ˆ y = u y x ( ) 0 0 + u y x ( ) 1 1 + ⋅⋅⋅ + u y x ( ) n n 。其回归分析过程为：由 Q = ∑ ( y i − ⇒ ) 2 ˆ y i min ， 令 0 Q ∂⎧ ⎪∂⎪⎪ u ⎨ M ⎪ ∂⎪ Q u ∂⎪⎩ n = 0 = 0 求得参数 0 u u 1, , u⋅⋅⋅ 即可。定义相关系数 , n R = l l xy l xx yy (0 ≤ R ≤ ，其中 1) l xx = −∑ x i ( i 2 x ) ， l yy = −∑ y i ( i 2 y ) l xy = ， ∑ i ( x i − x y )( i − y ) 。按数理统计理论，自由度 ( nµµ= − 与相 2) 关系数 Kα存在一定的关系。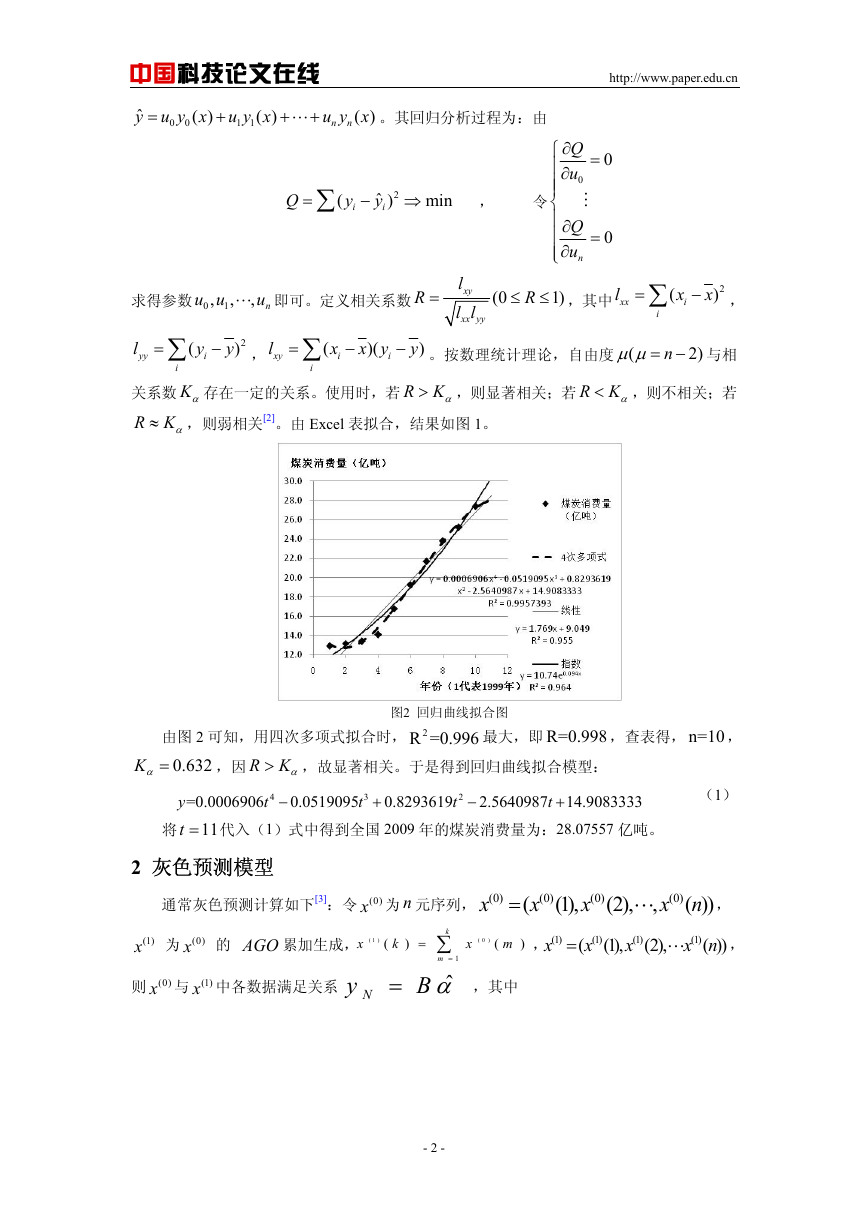使用时，若 R Kα> ，则显著相关；若 R Kα< ，则不相关；若 R Kα≈ ，则弱相关[2]。由 Excel 表拟合，结果如图 1。 图2 回归曲线拟合图 由图 2 可知，用四次多项式拟合时， 2R =0.996 最大，即 R=0.998 ，查表得， n=10 ， 0.632 ，因 R Kα> ，故显著相关。于是得到回归曲线拟合模型： Kα = 4 y t =0.0006906 t = 代入（1）式中得到全国 2009 年的煤炭消费量为：28.07557 亿吨。 14.9083333 t 0.8293619 t 0.0519095 2.5640987 将 11 − + − + t 2 3 （1） 2 灰色预测模型 x 通常灰色预测计算如下[3]：令 (0)x 为 n 元序列， (0) = ( x (0) (1), x (0) (1)x 为 (0)x 的 AGO 累加生成， ( 1 ) x Ny 则 (0)x 与 (1)x 中各数据满足关系 ( k = ∑ k ) ˆ Bα= m = 1 x ( 0 ) ( m ) x ， (1) = ( x (1) (1), ，其中 (2), , L x (2), (1) x (0) n ( )) ， x n ( )) (1) ， L - 2 - 

中国科技论文在线 http://www.paper.edu.cn y N ⎡ ⎢ ⎢ = ⎢ ⎢ ⎢ ⎣ x x x ( 0 ) ( 0 ) ( 2 ) (3) M ( ( 0 ) n ) ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ˆ a = ( T B B ) − 1 T B y N ， (1) (1) B x (2), 1 ⎤ ⎡ − ⎥ ⎢ x (3), 1 −⎢ ⎥ = ⎢ ⎥ M ⎥ ⎢ n x ( ), 1 ⎢− ⎥ ⎦ ⎣ 0.0956 −⎡ = ⎢ 10.1 512 ⎣ ⎤ ⎥ ⎦ M (1) ， ˆ a ⎡ = ⎢ ⎣ a b ⎤ ⎥ ⎦ ，解得 (1,1) GM 影子方程的解为： 1) + (1 ) ˆ x ( t 模型预测值为： = ( x ( 0 ) (1) − b / a e ) − a t + b / a ˆ x ( 0 ) 1) 于是得到灰色预测模型： + ( t = (1 ) ˆ x ( t + 1) − ˆ x (1 ) t ( ) (0) ˆ x t ( 1) 10.8572 + = e 0.0956 t (2) 将 10 t = 代入（3）式中得到全国 2009 年的煤炭需求量为：28.24233 亿吨。 3 最优组合预测模型 组合预测就是把多个基于不同假设条件下的预测模型的预测结果加权线性组合作为预 测结果的预测方法。组合预测模型包含了各单个模型所包含的有用信息，因此能改善模型的 拟合能力和提高预测精度。组合预测方法的关键是确定组合权系数[4]。 设t时刻的实际煤炭需求量为 ty ( t = 1 ,2 , ⋅ ⋅⋅ ， 1ty 表示回归曲线拟合模型t时刻的预 测值， 2ty 表示灰色预测模型t时刻的预测值， iw ( i = 1 2 )， 表示权系数。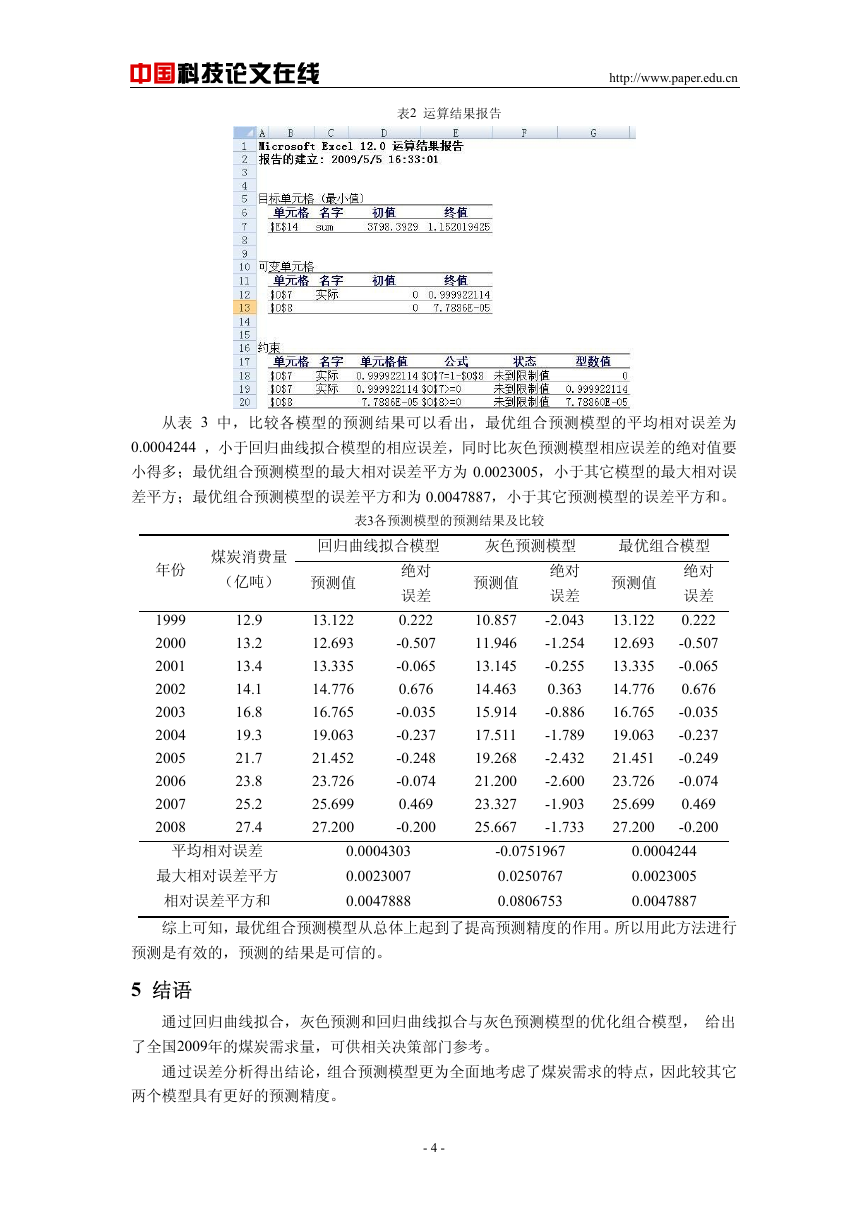建立如下权系 数优化模型: , n ) m in = n ∑ t= 1 (y t − w y 1 1 t − w y 2 2 t 2 ) st w w 1 + = 2 1 w w , 0 ≥ 1 2 ⎧ ⎨ ⎩ 选取表3中1999～2008年全国煤炭消费量及各模型预测结果，利用Excel表中的规划求解 功能求解，得到表2运算结果报告，即 1w = 0.999922 ， 2w = 0.000078 ，从而得到煤炭需 求组合预测模型： y = 0.999922y + 0.000078y （3） t 1t 2t 利用该组合模型对全国2009年的煤炭需求进行预测，结果为：28.07558亿吨。 4 模型分析 以上所建立的三种模型较其它预测模型的特点是，所需数据量最少，只从自身的发展趋 势来推断未来的发展，把与之相关的所有因素的影响都看作已蕴涵在其自身的成长过程中， 这种模型对于煤炭消费量变化趋势稳定时具有较高的准确性，并且可以用前期数据对以后几 个间隔期的消费量进行预测，这是其它预测模型所不具备的。 - 3 - 

中国科技论文在线 http://www.paper.edu.cn 表2 运算结果报告 从表 3 中，比较各模型的预测结果可以看出，最优组合预测模型的平均相对误差为 0.0004244 ，小于回归曲线拟合模型的相应误差，同时比灰色预测模型相应误差的绝对值要 小得多；最优组合预测模型的最大相对误差平方为 0.0023005，小于其它模型的最大相对误 差平方；最优组合预测模型的误差平方和为 0.0047887，小于其它预测模型的误差平方和。 表3各预测模型的预测结果及比较 年份 煤炭消费量 （亿吨） 预测值 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 12.9 13.2 13.4 14.1 16.8 19.3 21.7 23.8 25.2 27.4 平均相对误差 最大相对误差平方 相对误差平方和 回归曲线拟合模型 绝对 误差 0.222 -0.507 -0.065 0.676 -0.035 -0.237 -0.248 -0.074 0.469 -0.200 13.122 12.693 13.335 14.776 16.765 19.063 21.452 23.726 25.699 27.200 预测值 灰色预测模型 绝对 误差 -2.043 -1.254 -0.255 0.363 -0.886 -1.789 -2.432 -2.600 -1.903 -1.733 10.857 11.946 13.145 14.463 15.914 17.511 19.268 21.200 23.327 25.667 0.0004303 0.0023007 0.0047888 -0.0751967 0.0250767 0.0806753 预测值 最优组合模型 绝对 误差 13.122 0.222 -0.507 12.693 13.335 -0.065 14.776 0.676 -0.035 16.765 -0.237 19.063 21.451 -0.249 23.726 -0.074 25.699 0.469 27.200 -0.200 0.0004244 0.0023005 0.0047887 综上可知，最优组合预测模型从总体上起到了提高预测精度的作用。所以用此方法进行 预测是有效的，预测的结果是可信的。 5 结语 通过回归曲线拟合，灰色预测和回归曲线拟合与灰色预测模型的优化组合模型， 给出 了全国2009年的煤炭需求量，可供相关决策部门参考。 通过误差分析得出结论，组合预测模型更为全面地考虑了煤炭需求的特点，因此较其它 两个模型具有更好的预测精度。 - 4 - 

中国科技论文在线 http://www.paper.edu.cn 参考文献 [1] 国家统计局.中国能源统计年鉴2008 [M].北京:中国统计出版社，2009 [2] 林在康，郑西贵 矿业信息技术基础[M].徐州：中国矿业大学出版社，2009 [3] 刘涛，梁国军，汪春梅 灰色系统预测理论在矿井生产中的应用[J]．煤，2007年11月，第16卷 第11期 [4] 侯运炳，张文，张浩，彭勃，潘仁飞.煤炭需求最优组合预测[J]．煤炭工程，2007年第11期 Analysis of Prediction Model on Coal Demand CAI Wu1，YUAN Sha-sha2，Zhang Qiang1 1 School of Mine, China University of Mining and Technology, Xuzhou, Jiangsu (221116) 2 School of Computer Science and Technology, China University of Mining and Technology, Xuzhou, Jiangsu (221116) Abstract Based on the model of regression curve fitting, gray prediction and optimal combination, models for forecasting coal demand are built, With the model , the prediction of coal demand is made for 2009.Finally, the predictable results of the three models are discussed, come to the conclusion: the optimal combination forecasting model on the whole plays a role in improving prediction accuracy, using this method is effective, the predictable results are credible. Key words: Coal demand; Regression curve fitting; Gray prediction; Optimal combination forecasting 作者简介: 蔡武(1988-)，男，湖南桃江人，现中国矿业大学采矿工程 06 级在读本科生。 - 5 -