2011年山东青岛科技大学材料力学考研真题.doc

发布时间：2022-09-15 发布人：admin 分类：说明书资料大小：0.05M 资料格式：doc 举报版权申诉

第1页 / 共5页

第2页 / 共5页

第3页 / 共5页

第4页 / 共5页

第5页 / 共5页

文本预览

2011 年山东青岛科技大学材料力学考研真题一、判断对错（冬小题 3 分，共 30 分） 1.使杆件产生轴向拉压变形的外力必须是一对沿杆件轴线的集中力。（） 2.一空心圆截面直杆，其内、外径之比为 1 = 0.8,两端承受轴向拉力作用，如将内外径增加一倍，则其抗拉刚度将是原来的 8 倍。（） 3.圆轴受扭时，横截面上的最大切应力发生在截面形心处。（） 4.若将受扭实心圆轴的以径增加•倍，则其刚度是原来的 16 倍。（） 5.在平面图形的儿何性质中，静矩和惯性积的偵可正、可负、也可为零。 6.梁在集中力偶作用的截面处，它的内力图为 Ml#］冇突变，Q 图无变化。（） 7.包围一点一定有一个单元体，该单元体各面只有正应力而无切应力。（） 8.对一受静水压力的小球，小球的形状改变比能为零。（） 9.铸铁水管冬天结冰时会因冰膨胀而涨裂，而管内的冰不破碎，这是因为冰处丁•三向近似等压应力状态。（） 10.细长压杆受轴向压力作用凌轴向压力大于临界压力时，细长压杆不可能保持平衡。（）二.选择题（冬小题 4 分，共 40 分） 1 .胡克定律应用的条件是什么？（） A 只适用于塑性材料。 B 灌适用于轴向拉伸。 C 应力不超过比例极限。 D 应力不超过屈服极限。 2.应力与内力冇什么不同？（） A 内力大于应力 B 内力等于应力的代数和。 C 内力为矢量，而应力为标量。 D 进-步精确描写内力分布情况的物理量，它们的量纲不同 3. 布钢铝两根圆截面轴，其尺寸大小都相同。已知 E ffl=3E 当受帔矩 T 彘相同吋: A 钢轴的最大切应力和扭转伯都小丁•铝轴的。 B 钢轴的最大切应力和扭转角都等丁•铝轴的。 C 两轴的最大切应力相等，而钢轴的扭转角小丁•铝轴的 D 两轴的最大切应力相等，而钢轴的扭转伯大丁•铝轴的 4.关于抗弯刚度 EI 与抗弯截面模量 Wz 下列说法，那种止确？（） A 抗弯刚度与杆件材妙无关，用丁•计算最大弯曲正应力；抗弯截面模量与. 料冇关，用 T-TO 变形。

B 抗弯刚度与杆件材料冇关，与横截面形状和尺寸冇关，用丁•毋域*T；姓弯截面模量与材料无关，与横截面形状、尺寸冇关，用丁•计算强度。g C 抗君刚度与杆件的截面形状无关，抗君截面模量与排牛截面形状冇关。 D 抗君刚度与杆件的截面形状冇关，抗君截面模量与杆件截面形状无关。 5.关于转角可以这样描述：第一种，转角是指横截面的角位移。第二种，转角是指中性轴的角位移。第三种，转角是指形心在垂直方向的位移。下列答案中哪一个是正确的？ A 第一种说法正确。 B 第二种说法正确。 C 第三种说法正确。 D 三种说法都不正确。 6.应用叠加原理求梁位移时的条件是：（） A 必须是等截面的梁； B 必须是静定的梁； C 必须是小变形的梁； D 必须是平面弯曲的梁。 7.铸铁试件拉伸时，沿横截面断裂；扭转时沿与轴线成 450 倾角的螺旋面断裂。这与什么有关？（） A 最大切应力； B 最大拉应力； C 最大切应力和最大拉应力； D 最大切应变。 8.在纯剪切应力状态下，用第四强度理论可以证明：塑性材料的许用剪应力为 11 许用拉应力的关系：（） A [t] = [s]M/3 B [t] = [s]/3 C [t] = [s] D [t] = [s]/2 9.圆轴受轴向偏心压缩时，横截面上存在的内力应该有：（） A 只有轴力 B 只有弯矩 C 只有扭矩 D 轴力为 11 弯矩 10.应用单位载荷法算出构件上某处的位移是什么位移？（） A 是该点的总位移。 B 是该点都在某方向上的位移分量。 C 是该点沿单位载荷方向的相应位移。 D 是该点的实际位移。

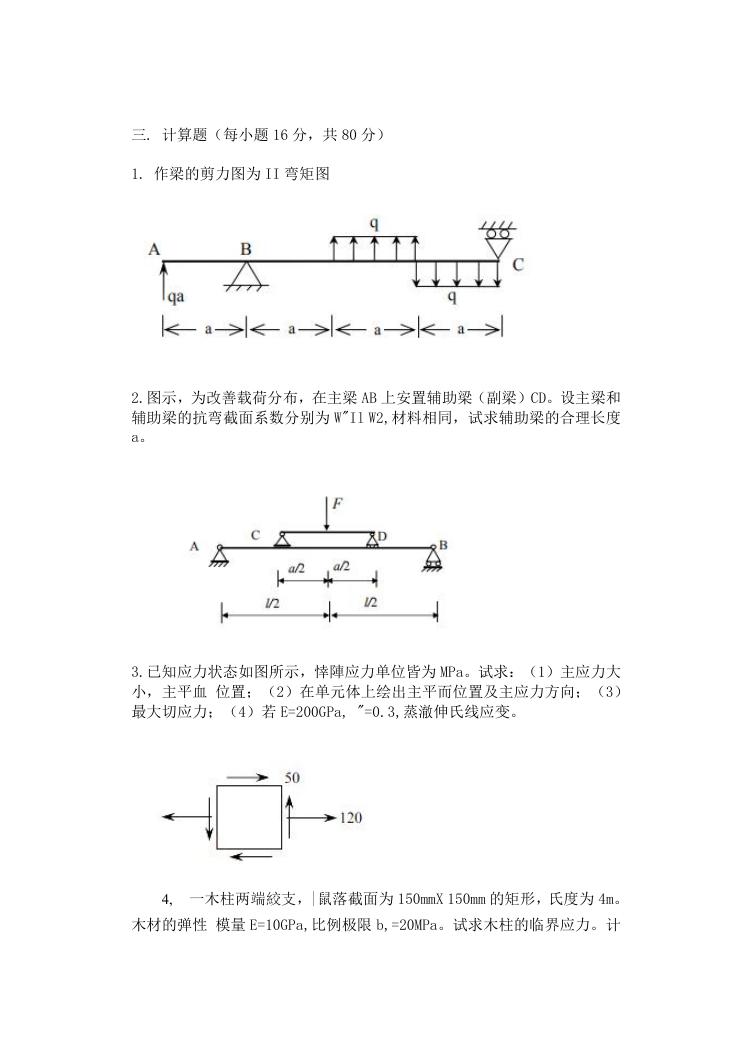
三. 计算题（每小题 16 分，共 80 分） 1. 作梁的剪力图为 II 弯矩图 2.图示，为改善载荷分布，在主梁 AB 上安置辅助梁（副梁）CD。设主梁和辅助梁的抗弯截面系数分别为 W"Il W2,材料相同，试求辅助梁的合理长度 a。 3.已知应力状态如图所示，悻陣应力单位皆为 MPa。试求：（1）主应力大小，主平血位置；（2）在单元体上绘出主平而位置及主应力方向；（3）最大切应力；（4）若 E=200GPa, "=0.3,蒸澈伸氏线应变。 4, 一木柱两端絞支，|鼠落截面为 150mmX 150mm 的矩形，氏度为 4m。木材的弹性模量 E=10GPa,比例极限 b,=20MPa。试求木柱的临界应力。计

算临界应力的公式冇（a）欧拉公式 j （b） g 线公式 OCr=2.87-0.19L. 5. 图示梁的抗弯刚度时为常数。试用能最法计算 B 截面的转伯和 C 截而挠度。

分享到：

赞收藏

资料库

2011年山东青岛科技大学材料力学考研真题.doc

相关推荐

考研

热门标签

最新资料