MATLAB计算微带线特性阻抗.docx

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：0.41M 资料格式：docx 举报版权申诉

liulianlalala-12041538-4744300845234059660.docx.pdf-第1页.png

第1页 / 共7页

liulianlalala-12041538-4744300845234059660.docx.pdf-第2页.png

第2页 / 共7页

liulianlalala-12041538-4744300845234059660.docx.pdf-第3页.png

第3页 / 共7页

liulianlalala-12041538-4744300845234059660.docx.pdf-第4页.png

第4页 / 共7页

liulianlalala-12041538-4744300845234059660.docx.pdf-第5页.png

第5页 / 共7页

liulianlalala-12041538-4744300845234059660.docx.pdf-第6页.png

第6页 / 共7页

liulianlalala-12041538-4744300845234059660.docx.pdf-第7页.png

第7页 / 共7页

MATLAB计算微带线特性阻抗

MATLAB 计算微带线特性阻抗实验目的：在射频电路及高速数字电路设计的过程中，传输线阻抗控制必不可少。微带线是最受欢迎的传输线形式，给定微带线线宽，微带线厚度，PCB 板材的相对介电常数εr ，设计一款计算器，这款计算器可以快速地计算出微带线的特征阻抗 Zo，而且这款计算器的准确度丝毫不逊于商业软件。实验原理：微带线的加工与印制电路工序基本一致。一种是采用双面聚四氟乙烯（ε r=2.1，tanδ=0.008）或聚四氟乙烯玻璃纤维（εr=2.55，tanδ=0.008）覆铜板，经照相制版、光刻腐蚀做成电路。再一种就是氧化铝陶瓷（εr=9.5-10，tan δ=0.0003）基片上用真空镀膜技术蒸发上电路。后一种加工工艺复杂，成本高，多用于特殊要求的场合。微波单片集成电路所用的半导体基片材料主要是砷化镓（εr=13，tanδ=0.006）。微带电路与普通晶体管印制电路的区别为：微带电路要求基片介质必须损耗小，不易变形，介电常数εr 的取值一般在 2-20 之间，金属板的导电性能要好，加工线条的精确度要高。微带线是一种最流行的平面传输线，主要是因为它可以用照相印制工艺来加工，而且它容易与其他有源和无源的微波器件集成。微带线的几何结构如图 2-1 （a）。宽度为 W 的导体印制在薄的、厚度为 d，相对介电常数为εr 的接地电介质基片上；其场力线的示意图如图 2-1（b）。严格地讲，微带线属于非均匀介质系统，在非均匀介质的结构中不存在 TEM 模，也不存在纯 TE 模或纯 TM 模，而是 TE 模和 TM 模的混合模。微带线可以看成是由平行双导线演变来的，假设在无限均匀介质中有一平行双导线线上传输的主模是纯 TEM 模，如果在两导线间的中心对称面上放置一个极薄的理想的导体板，将双导线从中心对称面分为.上下两部分，如果在任一单根导线和理想导体平板之间馈电，其间仍可传输纯 TEM 模，因而将未馈电的那一根导线移去，也不会改

变馈电的导线与理想导体平板场分布。把此馈电的导线变成扁平导体带，就形成了上半空间为同一种介质的微带线，若该介质是空气则称为空气微带线。对于空气介质的微带线,它是双导线系统,且周围是均匀的空气,因此它可以存在无色散的 TEM 模。若电介质不存在(εr=1),则我们可以把这个传输线想象成一个双线传输线，它由宽度为 W、分开距离为 2d 的两个平的带状导体组成(根据镜像理论接地平面可以拉开)。在这种情形下，我们应该有一个简单的 TEM 传输线，其中 vp=c,β =k0。电介质的的存在，特别是电介质没有填充带的.上边的区域(y>d)的实际情况，使得微带线的行为和分析复杂化。由于微带线不能支持纯的 TEM 波，因为在电介质区域的 TEM 场的相速应该是 c/ ，但是空气区域中的 TEM 场的相速却是 c。这样，在电解质、空气分界面上不可能实现 TEM 的波的相位匹配。一个是介质基片换成空气微带线单位长度电容 C1a;另一个是微带线单位长度电容 C1。特性阻抗 Z。和相位常数β可以用这两个电容表示为:

微带线的主要参数： 1. 等效介电常数(εeff): 2.特性阻抗（Zo）

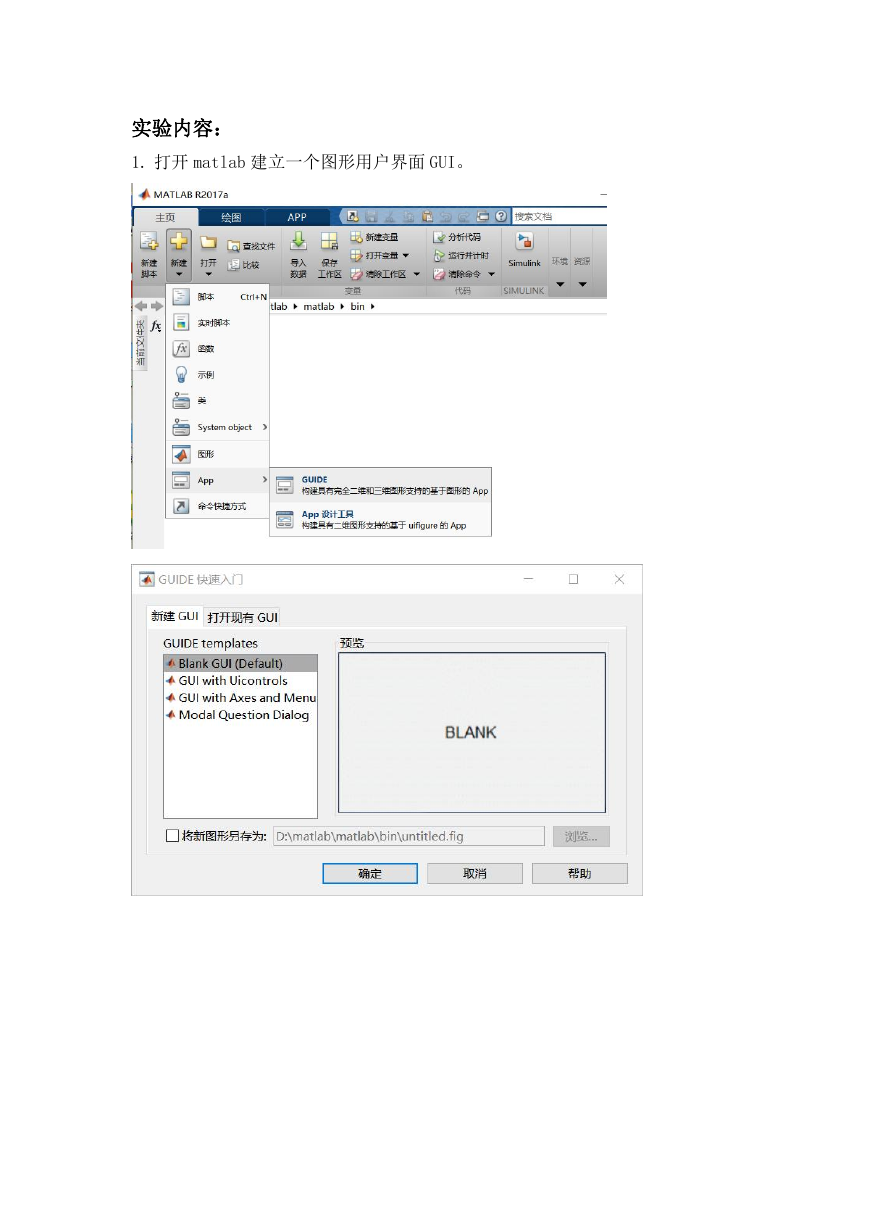
实验内容： 1. 打开 matlab 建立一个图形用户界面 GUI。

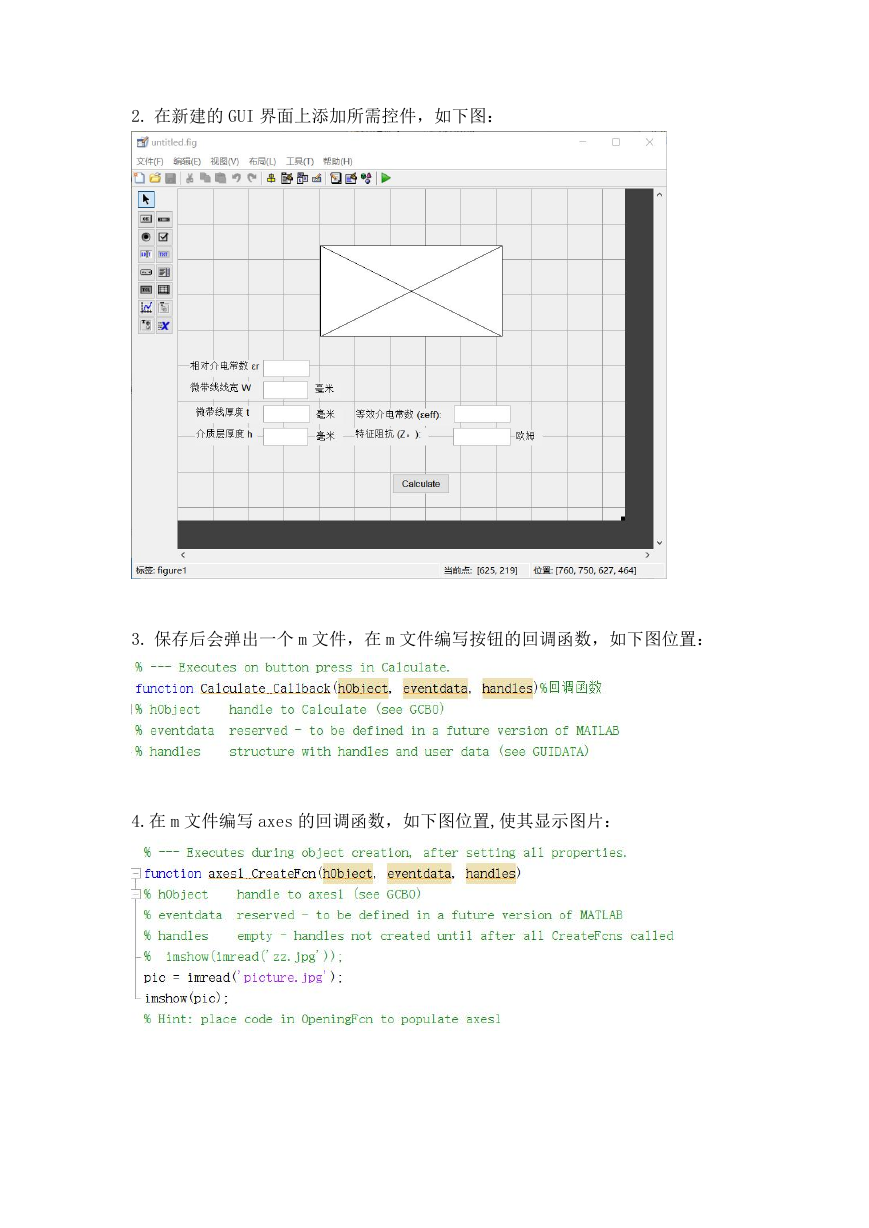
2. 在新建的 GUI 界面上添加所需控件，如下图： 3. 保存后会弹出一个 m 文件，在 m 文件编写按钮的回调函数，如下图位置： 4.在 m 文件编写 axes 的回调函数，如下图位置,使其显示图片：

handle to Calculate (see GCBO) structure with handles and user data (see GUIDATA) 实验程序： % --- Executes on button press in Calculate. function Calculate_Callback(hObject, eventdata, handles)%回调函数 % hObject % eventdata reserved - to be defined in a future version of MATLAB % handles str1=get(handles.line_er,'string');%先取出值εr er=str2num(str1); str2=get(handles.line_w,'string');%先取出值 w w=str2num(str2); str3=get(handles.line_t,'string');%先取出值 t t=str2num(str3); str5=get(handles.line_h,'string');%先取出值 h h=str2num(str5); m = (t/h)^2+((1/pi)/(w/t+1.1))^2; n = (1+1/er)/2; w0 = (t/pi)*log(4*exp(1)/m); w1 = w0*n; w2 = w+w1; a = 4*h/w2; b = (14+8/er)/11; c = (b^2)*(a^2)+n*pi^2; Zo = 120*pi/(2*sqrt(2)*pi*sqrt(er+1))*log(1+a*(b*a+sqrt(c))); e1 = (er+1)/2; e2 = (er-1)/2; f = 1/sqrt(1+(12*h/w)); if w/h<1 else end str5 = num2str(Zo) set(handles.line_z0, 'string',str5); %将之前计算的 num 型再次转换成字符串然后输入到第 5 个格子里。 str6 = num2str(Eeff) set(handles.line_Eeff,'string',str6); %将之前计算的 num 型再次转换成字符串然后输入到第 6 个格子里。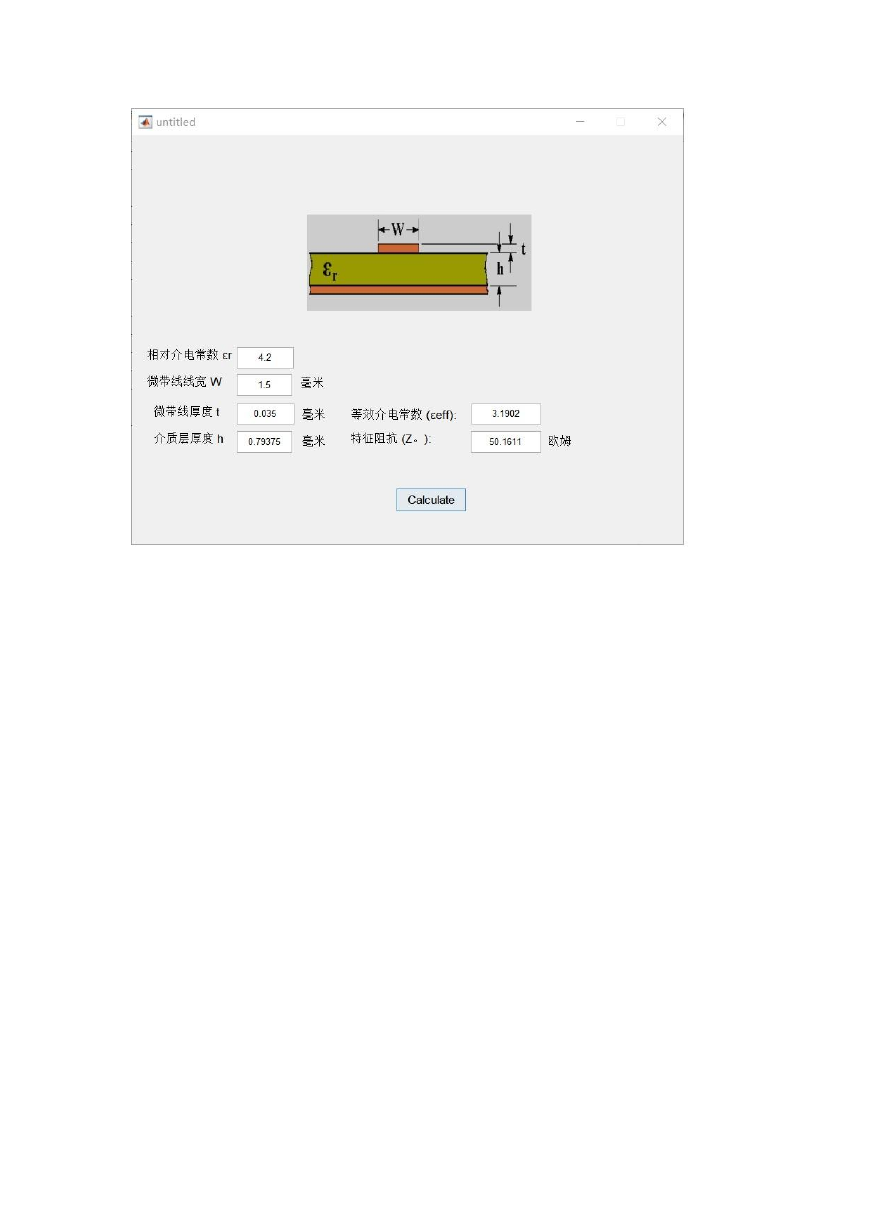 Eeff = e1+e2*(f+0.04*(1-(w/h))^2); Eeff = e1+e2*f; 实验结果：

分享到：

赞收藏

资料库

MATLAB计算微带线特性阻抗.docx

相关推荐

课程资源

热门标签

最新资料