logo资料库

三次Bezier曲线原理及实现代码.doc

发布时间：2022-06-03 发布人：admin 分类：说明书 资料大小：0.87M 资料格式：doc 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    Bezier曲线原理及实现代码（c++）
    二次方贝塞尔曲线的路径由给定点 P0、P1、P2 的函数 B(t) 追踪：
    P0、P1、P2、P3 四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于 P0 走向 P
    曲线的
    现代的成象系统，如
    一般化
     
     
     
     
    P0、P1、…、Pn，其贝塞尔曲线即
    例如 ：
    如上公式可如下递归表达： 用
    用平常话来说， 阶贝塞尔曲线之间的插值。
    一些关于参数曲线的术语，有
    即多项式
    又称作 n 阶的
    点 Pi 称作贝塞尔曲线的控制点。
     
     
    线性贝塞尔曲线函数中的 t 会经过由 P0 至P1 的 B(t) 所描述的曲线。例如当 t=0.25
    为建构二次贝塞尔曲线，可以中介点 Q0 和 Q1 作为由 0 至 1 的 t：
    由 P0 至 P1 的连续点 Q0，描述一条线性贝塞尔曲线。
    由 P1 至 P2 的连续点 Q1，描述一条线性贝塞尔曲线。
    由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线。
     
    为建构高阶曲线，便需要相应更多的中介点。对于三次曲线，可由线性贝塞尔曲线描述的中介点 Q0、Q1、Q
    对于四次曲线，可由线性贝塞尔曲线描述的中介点 Q0、Q1、Q2、Q3，由二次贝塞尔曲线描述的点 R0
    P(t)=(1-t)P0+tP1 ,
    　　P(t)=(1-t)3P0+3t(1-t)2P1+3t2(1-t)P2+t3P3 矩阵表示为：
    二、算法（c++）
    工程目录是:Win32App vc6.0#include#includ
      HDC hdc;  static POINT pt[NUM];  TEXTMETRIC tm
    Bezier 曲线原理及实现代码（c++） 一、原理： 贝塞尔曲线于 1962 年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他 运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由 Paul de Casteljau 于 1959 年 运用 de Casteljau 算法开发，以稳定数值的方法求出贝塞尔曲线。 线性贝塞尔曲线 给定点 P0、P1，线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出： 且其等同于线性插值。 二次方贝塞尔曲线的路径由给定点 P0、P1、P2 的函数 B(t) 追踪： 。 TrueType 字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。 P0、P1、P2、P3 四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于 P0 走向 P1，并从 P2 的方向来到 P3。一般不会经过 P1 或 P2；这两个点只是在那里提供 方向资讯。 P0 和 P1 之间的间距，决定了曲线在转而趋进 P3 之前，走向 P2 方向的“长 度有多长”。 曲线的参数形式为： 。 现代的成象系统，如 PostScript、Asymptote 和 Metafont，运用了以贝塞尔样条 组成的三次贝塞尔曲线，用来描绘曲线轮廓。 一般化
    P0、P1、…、Pn，其贝塞尔曲线即 。 例如 ： 。 如上公式可如下递归表达： 用 表示由点 P0、P1、…、Pn 所决定的贝塞尔 曲线。则 用平常话来说， 阶贝塞尔曲线之间的插值。 一些关于参数曲线的术语，有 即多项式 又称作 n 阶的伯恩斯坦基底多项式，定义 00 = 1。 点 Pi 称作贝塞尔曲线的控制点。多边形以带有线的贝塞尔点连接而成，起始于 P0 并以 Pn 终止，称作贝塞尔多边形（或控制多边形）。贝塞尔多边形的凸包（convex hull） 包含有贝塞尔曲线。
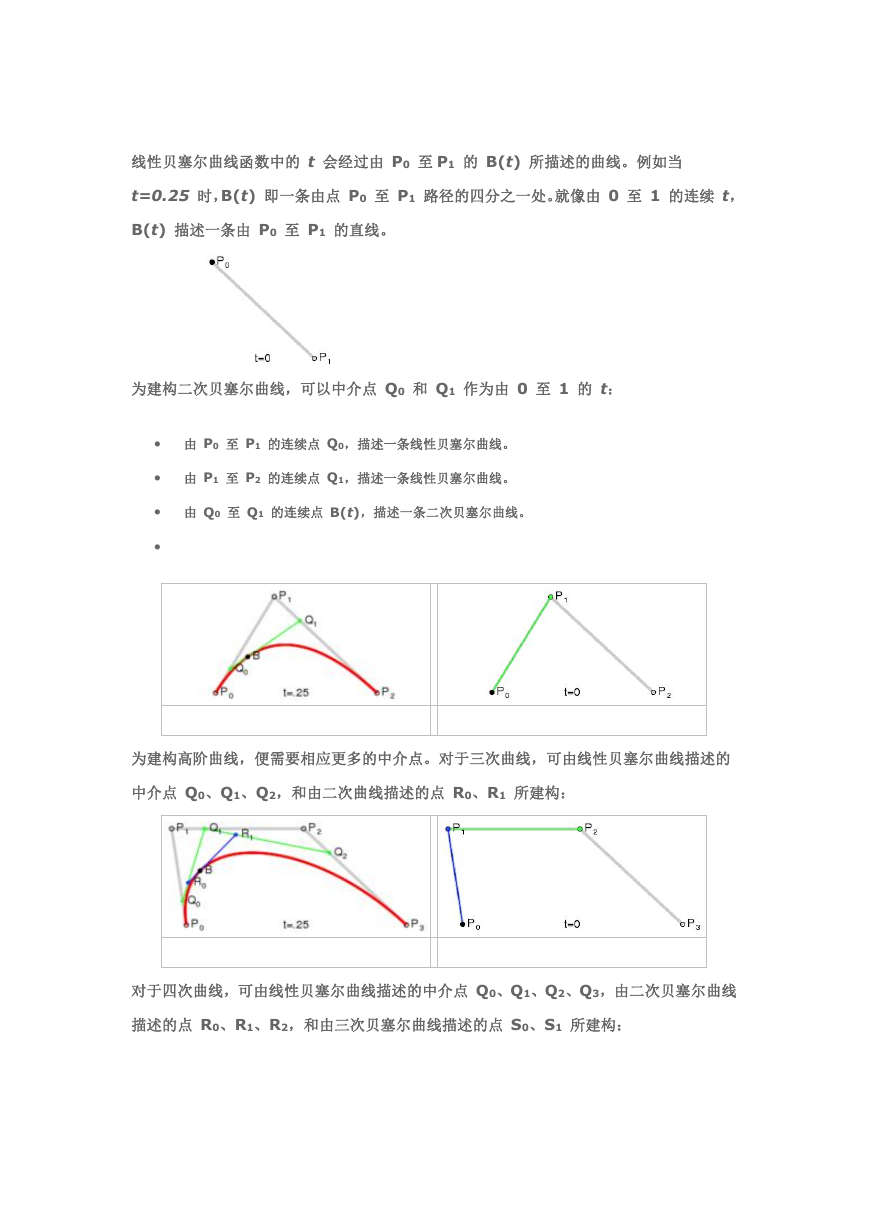
    线性贝塞尔曲线函数中的 t 会经过由 P0 至 P1 的 B(t) 所描述的曲线。例如当 t=0.25 时，B(t) 即一条由点 P0 至 P1 路径的四分之一处。就像由 0 至 1 的连续 t， B(t) 描述一条由 P0 至 P1 的直线。 为建构二次贝塞尔曲线，可以中介点 Q0 和 Q1 作为由 0 至 1 的 t：  由 P0 至 P1 的连续点 Q0，描述一条线性贝塞尔曲线。  由 P1 至 P2 的连续点 Q1，描述一条线性贝塞尔曲线。  由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线。  为建构高阶曲线，便需要相应更多的中介点。对于三次曲线，可由线性贝塞尔曲线描述的 中介点 Q0、Q1、Q2，和由二次曲线描述的点 R0、R1 所建构： 对于四次曲线，可由线性贝塞尔曲线描述的中介点 Q0、Q1、Q2、Q3，由二次贝塞尔曲线 描述的点 R0、R1、R2，和由三次贝塞尔曲线描述的点 S0、S1 所建构：
    P(t)=(1-t)P0+tP1 , 。 矩阵表示为： ， P(t)=(1-t)2P0+2t(1-t)P1+t2P2, 矩阵表示为： 。 。 P(t)=(1-t)3P0+3t(1-t)2P1+3t2(1-t)P2+t3P3 ， 。 矩阵表示为： （6－3－2） ， 。 在（6－3－2）式中，Mn+1 是一个 n＋1 阶矩阵，称为 n 次 Bezier 矩阵。 ， 。 （6－3－3） 其中， 。
    利用（6－3－3）式，我们可以得到任意次 Bezier 矩阵的显式表示，例如 4 次和 5 次 Bezier 矩阵为： ， 可以证明，n 次 Bezier 矩阵还可以表示为递推的形式： （6－3－4） 二、算法（c++） 工程目录是:Win32App vc6.0 #include #include #include #define NUM 10
    LRESULT CALLBACK Winproc(HWND,UINT,WPARAM,LPARAM); int WINAPI WinMain(HINSTANCE hInstance,HINSTANCE hPrevInstanc,LPSTR lpCmdLine,int nShowCmd) { MSG msg; static TCHAR szClassName[] = TEXT("::Bezier 样条计算公式由 法国雷诺汽车公司的工程师 Pierm Bezier 于六十年代提出"); HWND hwnd; WNDCLASS wc; wc.cbClsExtra =0; wc.cbWndExtra =0; wc.hbrBackground = (HBRUSH)GetStockObject(WHITE_BRUSH); wc.hCursor = LoadCursor(NULL,IDC_ARROW); wc.hIcon = LoadIcon(NULL,IDI_APPLICATION); wc.hInstance = hInstance; wc.lpfnWndProc = Winproc; wc.lpszClassName = szClassName; wc.lpszMenuName = NULL; wc.style = CS_HREDRAW|CS_VREDRAW; if(!RegisterClass(&wc)) { MessageBox(NULL,TEXT("注册失败"),TEXT("警告框 "),MB_ICONERROR); return 0; } hwnd = CreateWindow(szClassName,szClassName, WS_OVERLAPPEDWINDOW,
    CW_USEDEFAULT,CW_USEDEFAULT, CW_USEDEFAULT,CW_USEDEFAULT, NULL,NULL,hInstance,NULL); ShowWindow(hwnd,SW_SHOWMAXIMIZED); UpdateWindow(hwnd); while(GetMessage(&msg,NULL,0,0)) { TranslateMessage(&msg); DispatchMessage(&msg); } return msg.wParam; } LRESULT CALLBACK Winproc(HWND hwnd,UINT message, WPARAM wparam,LPARAM lparam) { HDC hdc; static POINT pt[NUM]; TEXTMETRIC tm; static int cxClient,cyClient; HPEN hpen; int i,j,k,n,t; switch(message) { case WM_CREATE: static int cxchar;
    hdc = GetDC(hwnd); GetTextMetrics(hdc,&tm); cxchar = tm.tmAveCharWidth; ReleaseDC(hwnd,hdc); case WM_SIZE: cxClient = LOWORD(lparam); cyClient = HIWORD(lparam); return 0; case WM_PAINT: hdc = GetDC(hwnd); srand(time(0)); Rectangle(hdc,0,0,cxClient,cyClient); for(i=0; i<500; i++) { SelectObject(hdc,GetStockObject(WHITE_PEN)); PolyBezier(hdc,pt,NUM); for(j=0; j
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料