第1页 / 共25页
第2页 / 共25页
第3页 / 共25页
第4页 / 共25页
第5页 / 共25页
第6页 / 共25页
第7页 / 共25页
第8页 / 共25页
数学建模层次分析法案例大学毕业生就业选择问题.doc
一、问题举例：
二、问题分析：
三、确定各层次互相比较的方法——成对比较矩阵和权向量
四：一致性矩阵
一致性矩阵（一致阵）性质：
解释：
分析：
问题：Remark
五、一致性检验——一致性指标：
1．一致性检验指标的定义和确定——（平均值）的定义：
2．随机一致性检验指标——
3. 一致性检验指标的定义——一致性比率。
六、标度——比较尺度解：
七、组合权向量的计算——层次总排序的权向量的计算
八、层次分析法的基本步骤：
九、特征根的近似求法（实用算法）
1．“和法”求最大特征根和对应特征向量（近似解）
2．“根法”求最大特征根特征向量近似值：
3．“幂法”求最大特征根：
十、应用实例
层次分析法建模
层次分析法（AHP－Analytic Hierachy process）---- 多目标决策方法
70 年代由美国运筹学家 T·L·Satty 提出的，是一种定性与定量分析相结合的多目标决策
分析方法论。吸收利用行为科学的特点，是将决策者的经验判断给予量化，对目标（因素）结
构复杂而且缺乏必要的数据情况下，採用此方法较为实用，是一种系统科学中，常用的一种系
统分析方法，因而成为系统分析的数学工具之一。
传统的常用的研究自然科学和社会科学的方法有：
机理分析方法：利用经典的数学工具分析观察的因果关系；
统计分析方法：利用大量观测数据寻求统计规律，用随机数学方法描述（自然现象、
社会现象）现象的规律。
基本内容：（1）多目标决策问题举例 AHP 建模方法
（2）AHP 建模方法基本步骤
（3）AHP 建模方法基本算法
（3）AHP 建模方法理论算法应用的若干问题。
参考书： 1、姜启源，数学模型（第二版，第 9 章；第三版，第 8 章），高等教育出版社
2、程理民等， 运筹学模型与方法教程，（第 10 章），清华大学出版社
3、《运筹学》编写组，运筹学（修订版），第 11 章，第 7 节，清华大学出版社
一、问题举例：
A．大学毕业生就业选择问题
获得大学毕业学位的毕业生，“双向选择”时，用人单位与毕业生都有各自的选择标准和要
求。就毕业生来说选择单位的标准和要求是多方面的，例如：
1 能发挥自己的才干为国家作出较好贡献（即工作岗位适合发挥专长）；
2 工作收入较好（待遇好）；
3 生活环境好（大城市、气候等工作条件等）；
4 单位名声好（声誉-Reputation）；
5 工作环境好（人际关系和谐等）
6 发展晋升（promote, promotion）机会多（如新单位或单位发展有后劲）等。
问题：现在有多个用人单位可供他选择，因此，他面临多种选择和决策，问题是他将如何
作出决策和选择？——或者说他将用什么方法将可供选择的工作单位排序？
工作选择
贡献
收入
发展
声誉
工作环境
生活环境
1
可供选择的单位 P1’ P2 ‘
----- Pn
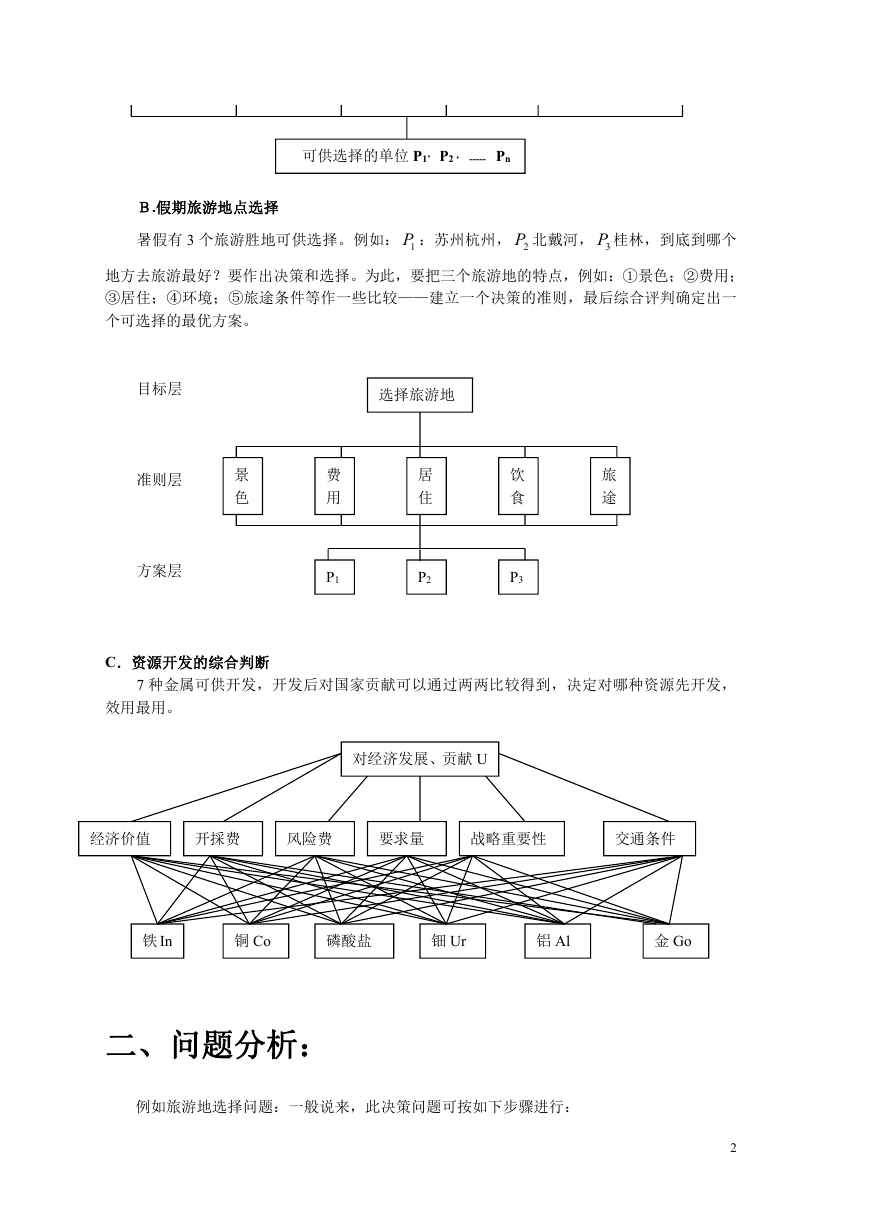
Ｂ.假期旅游地点选择
暑假有 3 个旅游胜地可供选择。例如： 1P ：苏州杭州， 2P 北戴河， 3P 桂林，到底到哪个
地方去旅游最好？要作出决策和选择。为此，要把三个旅游地的特点，例如：①景色；②费用；
③居住；④环境；⑤旅途条件等作一些比较——建立一个决策的准则，最后综合评判确定出一
个可选择的最优方案。
目标层
选择旅游地
准则层
景
色
方案层
费
用
P1
居
住
P2
饮
食
P3
旅
途
C．资源开发的综合判断
7 种金属可供开发，开发后对国家贡献可以通过两两比较得到，决定对哪种资源先开发，
效用最用。
对经济发展、贡献 U
经济价值
开採费
风险费
要求量
战略重要性
交通条件
铁 In
铜 Co
磷酸盐
钿 Ur
铝 Al
金 Go
二、问题分析：
例如旅游地选择问题：一般说来，此决策问题可按如下步骤进行：
2
（S1）将决策解分解为三个层次，即：
目标层：（选择旅游地）
准则层：（景色、费用、居住、饮食、旅途等 5 个准则）
方案层：（有 1P ， 2P ， 3P 三个选择地点）
并用直线连接各层次。
（S2）互相比较各准则对目标的权重，各方案对每一个准则的权重。这些权限重在人的思维过
程中常是定性的。
例如：经济好，身体好的人：会将景色好作为第一选择；
中老年人：会将居住、饮食好作为第一选择；
经济不好的人：会把费用低作为第一选择。
而层次分析方法则应给出确定权重的定量分析方法。
（S3）将方案后对准则层的权重，及准则后对目标层的权重进行综合。
（S4）最终得出方案层对目标层的权重，从而作出决策。
以上步骤和方法即是 AHP 的决策分析方法。
三、确定各层次互相比较的方法——成对比较
矩阵和权向量
在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因
而 Santy 等人提出：一致矩阵法
．．．．．
即：1. 不把所有因素放在一起比较，而是两两相互比较
2. 对此时採用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，提高准确度。
因素比较方法 —— 成对比较矩阵法：
目的是，要比较某一层 n 个因素
,
CC
1 对上一层因素 O 的影响（例如：旅游决策解
,
nC
,
2
中，比较景色等 5 个准则在选择旅游地这个目标中的重要性）。
採用的方法是：每次取两个因素 iC 和 jC 比较其对目标因素 O 的影响，并用 ija 表示，全部
比较的结果用成对比较矩阵表示，即：
A
(
a
ij
)
nxn
,
a
ij
,0
a
ji
( 1
a
ij
或
a
ij
a
ij
)1
（1）
由于上述成对比较矩阵有特点：
A
(
a
ij
, )
a
ij
,0
a
ij
1
a
ji
故可称 A 为正互反矩阵：显然，由
a
ij
1 ，即：
a
ji
a
ij a
ji
1
，故有：
1jia
3
例如：在旅游决策问题中：
12 a
1
=
2
C
（景色）
1
C
（费用）
2
表示：
C
（
景色）对目标
1
C
（费用）对目标
2
O
1
的重要性为
O
2
的重要性为
故：
12 a
1
1
(2
即景色重要性为
，费用重要性为
2
）
a
13
4
4
1
=
C
（景色）
1
C
（居住条件）
3
表示：
即：景色为 4，居住为 1。
(
C
景色）对目标
1
C
（居住条件）对目标
3
O
的重要性为
4
O
1
的重要性为
的重要性为
7
O
1
的重要性为
a
23
7
7
1
=
O
表示：
C
（费用）
2
C
（居住条件）
3
(
C
费用）对目标
2
C
（居住条件）对目标
3
即：费用重要性为 7，居住重要性为 1。
33
55
1
2
11
11
1
4
2
7
1
1
17
1
2
5
1
3
5
1
2
1
1
1
4
3
3
A
3
1
因此有成对比较矩阵：
？？问题：稍加分析就发现上述成对比较矩阵的问题：
1 即存在有各元素的不一致性，例如：
既然：
a
12
C
1
C
2
a
21
1
2
;2
a
13
所以应该有：
a
23
C
C
2
3
a
a
21
31
C
2
C
3
C
1
C
1
而不应为矩阵 A 中的
23 a
7
1
a
31
4
1
1
a
13
1
4
8
8
1
C
1
C
3
2
1
4
②成对比较矩阵比较的次数要求太
，因： n 个元素比较次数为：
2
Cn
)1
(
nn
!2
次，
因此，问题是：如何改造成对比较矩阵，使由其能确定诸因素
,1 对上层因素 O 的
C
,
nC
权重？
对此 Saoty 提出了：在成对比较出现不一致情况下，计算各因素
,1 对因素（上层
C
,
nC
因素）O 的权重方法，并确定了这种不一致的容许误差范围。
为此，先看成对比较矩阵的完全一致性——成对比较完全一致性
4
四：一致性矩阵
Def：设有正互反成对比较矩阵：
A
a
11
a
21
W
1
W
1
W
2
W
1
1
a
12
a
22
2
W
1
W
W
W
2
2
, 1
,
a
1
n
, 1
,
a
2
n
W
1
W
n
W
W
2
n
a
ij
W
i
W
j
a
1
n
W
n
W
1
a
n
2
W
W
n
2
a
nn
W
W
n
n
1
(4)
除满足：（i）正互反性：即
a
ij
0
a
ij
( 1
a
或
a
ji
a
ji
ij
)1
而且还满足：（ii）一致性：即
a
ij
a
a
i
j
ka
i
a
kj
ha
i
ha
j
j i,
1,
2,
n
则称满足上述条件的正互反对称矩阵 A 为一致性矩阵，简称一致阵。
一致性矩阵（一致阵）性质：
性质 1： A 的秩 Rank(A)=1
A 的唯一非 0 的特征根为 n
性质 2： A 的任一列（行）向量都是对应特征根 n 的特征向量：
即有(特征向量、特征值)：
A
n
2
2
W
1
W
W
W
W
W
1
1
W
W
1
W
W
2
W
W
1
n
W
W
n
n
W
W
1
W
W
2
2
2
n
n
，则向量
W
2
W
1
W
W
3
5
满足：
WA
W
1
W
1
W
n
W
1
2
W
W
1
1
W
W
W
W
W
W
n
n
n
2
n
2
W
1
W
W
n
nW
1
nW
2
nW
n
Wn
即：
(
A
WnI
)
0
启发与思考：既然一致矩阵有以上性质，即 n个元素 W1, W2,W3 , …Wn 构成的向量
是一致矩阵 A 的特征向量，则可以把向量 W 归一化后的向量，看成是诸元素 W1, W2,W3 , …Wn
目标的权向量，因此，可以用求 A的特征根和特征向量的办法，求出元素 W1, W2,W3 , …Wn相对于
目标 O 的劝向量。
W
1
W
2
nW
W
解释：
一致矩阵即： n 件物体
MM
,
1
,
，它们重量分别为
nM
,
2
WW
,
1
,
，将他们两两比较
nW
,
2
重量，其比值构成一致矩阵，若用重量向量
W
W
1
W
2
nW
右乘 A ，则
为特征根的特征向量为
：重量向量
，＝
则归一化后的特征向量
W
W
1
W
2
nW
：
,
n
n
A
的特征根为
以
权向量，此种用特征向
W＝
W
1
W
1W
＝
，就表示诸因素
C
i
，C，，C
1
2
对上层因素O的权重，
为即
n
量
称特征根法，
求权向量的方法
6
分析：
若重量向量
W
2
W
1
W
nW
未知时，则可由决策者对物体
MM
,
1
,
之间两两相比关系，
nM
,
2
主观作出比值的判断，或用 Delphi（调查法）来确定这些比值，使 A 矩阵（不一定有一致性）
为已知的，并记此主观判断作出的矩阵为（主观）判断矩阵 A ，并且此 A （不一致）在不一致
的容许范围内，再依据： A 的特征根或和特征向量W 连续地依赖于矩阵的元素 ija ，即当 ija 离
一致性的要求不太远时， A 的特征根i 和特征值（向量）W 与一致矩阵 A 的特征根和特征向
量W 也相差不大的道理：由特征向量W 求权向量W 的方法即为特征向量法，并由此引出一致
性检查的方法。
问题：Remark
以上讨论的用求特征根来求权向量W 的方法和思路，在理论上应解决以下问题：
1． 一致阵的性质 1 是说：一致阵的最大特征根为 n （即必要条件），但用特征根来求特征向量
时，应回答充分条件：即正互反矩阵是否存在正的最大特征根和正的特征向量？且如果正互
反矩阵 A 的最大特征根
nmax
时， A 是否为一致阵？
2． 用主观判断矩阵 A 的特征根和特征向量W 连续逼近一致阵 A 的特征根和特征向量W
时，即： 由
得到：
即：
lim
k
k
k
lim
k
lim
k
WW k
Ak
A
是否在理论上有依据。
3．一般情况下，主观判断矩阵 A 在逼近于一致阵 A 的过程中，用与 A 接近的 *A 来代替 A ，
即有
A *
A
，这种近似的替代一致性矩阵 A 的作法，就导致了产生的偏差估计问题，即一致
性检验问题，即要确定一种一致性检验判断指标，由此指标来确定在什么样的允许范围内，
主观判断矩阵是可以接受的，否则，要
两两比较构造主观判断矩阵。此问题即一致性检
验问题的内容。
以上三个问题：前两个问题由数学严格比较可获得（见教材 P325，定理 1、定理 2）。第
7
3 个问题：Satty 给出一致性指标（TH1,TH2 介绍如下：）
附：
Th1：（教材 P326，perronTh 比隆 1970 ）对于正矩阵 A （ A 的所有元素为正数）
（1） A 的最大特征根是正单根；
（2）对应正特征向量W （W 的所有分量为正数）
lim
k
（3）
k
eA
T
k
eAe
1
1
1
证明：（3）可以通过将 A 化为标准形证明
其中：
W
e
为半径向量，W 是对应的归一化特征向量
Th2： n 阶正互反阵 A 的最大特征根
n ；
当
n 时， A 是一致阵
五、一致性检验——一致性指标：
1．一致性检验指标的定义和确定—— IC （平均值）的定义：
当人们对复杂事件的各因素，采用两两比较时，所得到的主观判断矩阵 A ，一般不可直接
保证正互反矩阵 A 就是一致正互反矩阵 A ，因而存在误差（及误差估计问题）。这种误差，必
然导致特征值和特征向量之间的误差
(
－及
WW)
。此时就导致问题
WA ＝
Wmax
与问
题
AW
nW
之间的差别。（上述问题中 max 是主观判断矩阵 A 的特征值，W 是带有偏差的相
对权向量）。这是由判断矩阵不一致性所引起的。
因此，为了避免误差太大，就要衡量主观判断矩阵 A 的一致性。
因为：
①当主观判断矩阵 A 为一致阵 A 时就有：
n
＝
k
k
1
n
n
1
k
n
k
1
a
kk
n
k
1
1
n
A 为一致阵时有：
1iia
（a[ii]为对角线
上的值，按照一致性矩阵的理解，它应该为 1）
此时存在唯一的非
max
n
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
