第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
MATLAB解偏微分方程.docx
1.绝热细杆的无源导热方程
2.弦的无阻尼自由振动方程
22=222
=
其中，t 是时间，x 是横坐标，u 是温度;
=,c 是物质的比热容，ρ是细杆的线密度
其中，t 是时间，x 是横坐标，u 是弦的横向位移;
=,T 是弦上的纵向张力，ρ是弦的线密度
其中，x 是横坐标，y 是纵坐标，，u 是稳定的温度;
22+22=0
3.拉普拉斯方程（常用于稳态引力场 稳态静电场 稳态温度场）
一.绝热细杆的无源导热方程
=
1.为便于求解，给定如下边值条件
其中，t 是时间，x 是横坐标，u 是温度;
=,c 是物质的比热容，ρ是细杆的线密度
>0 边值
=0,=1,=1,=1
0<<1 初场
,=0=
2.为便于求解令=，令,为横坐标值和时间值
∆ ，∆为时间间隔。
时间项使用向前差分，即=,+−,
空间项使用二阶中心差分，即=+,−,+−,
∆
=+,−,+−,
原式可变为 ,+−,
∆
∆
,+= ∆∆+,+(− ∆∆),+ ∆∆−,
移项和整理成如下形式
3.按稳定性条件∆∆<.,所以取时间间隔∆=0.0001s,空间间隔∆=0.02
，∆为空间间隔。
4.Matlab 编程如下
%% 左边值
%% 右边值
%% 给定边值，时间间隔，空间间隔,稳定性条件
u_a=1;
u_b=1;
deta_t=0.0001; %% 时间间隔
Total_time=0.5; %% 总时长
deta_x=0.02;
n=1:51;
sigma=deta_t/(deta_x^2);
k=0;
%% 一维杆的初值
u(1)=u_a;
u(51)=u_b;
for i=2:50
%% 空间间隔
%% 节点序号
%% 时刻标志位，用于绘图
%% 左边值
%% 右边值
u(i)=(i-1)/50;
%% 初始时刻的函数
end
plot((n-1)/50,u,'r');
hold on
%% 时间步进
%% 画出初始时刻温度图
for j=0:deta_t:Total_time
%% 左边界值，在该问题中不随时间变化
%% 左边界值，在该问题中不随时间变化
u_next(1)=u(1);
u_next(51)=u(51);
%% 计算下一时刻温度值
for i=2:50
u_next(i)=sigma*u(i-1)+(1-2*sigma)*u(i)+sigma*u(i+1);
end
%% 交换数据与绘图
u=u_next;
k=k+1;
if(mod(k,1000)==0)
plot((n-1)/50,u,'-');
end
end
%% 绘图修正
xlabel('X 值');
ylabel('温度');
legend('0 秒','0.1 秒','0.2 秒','0.3 秒','0.4 秒','0.5 秒');
axis([0 1 0 1.2]);
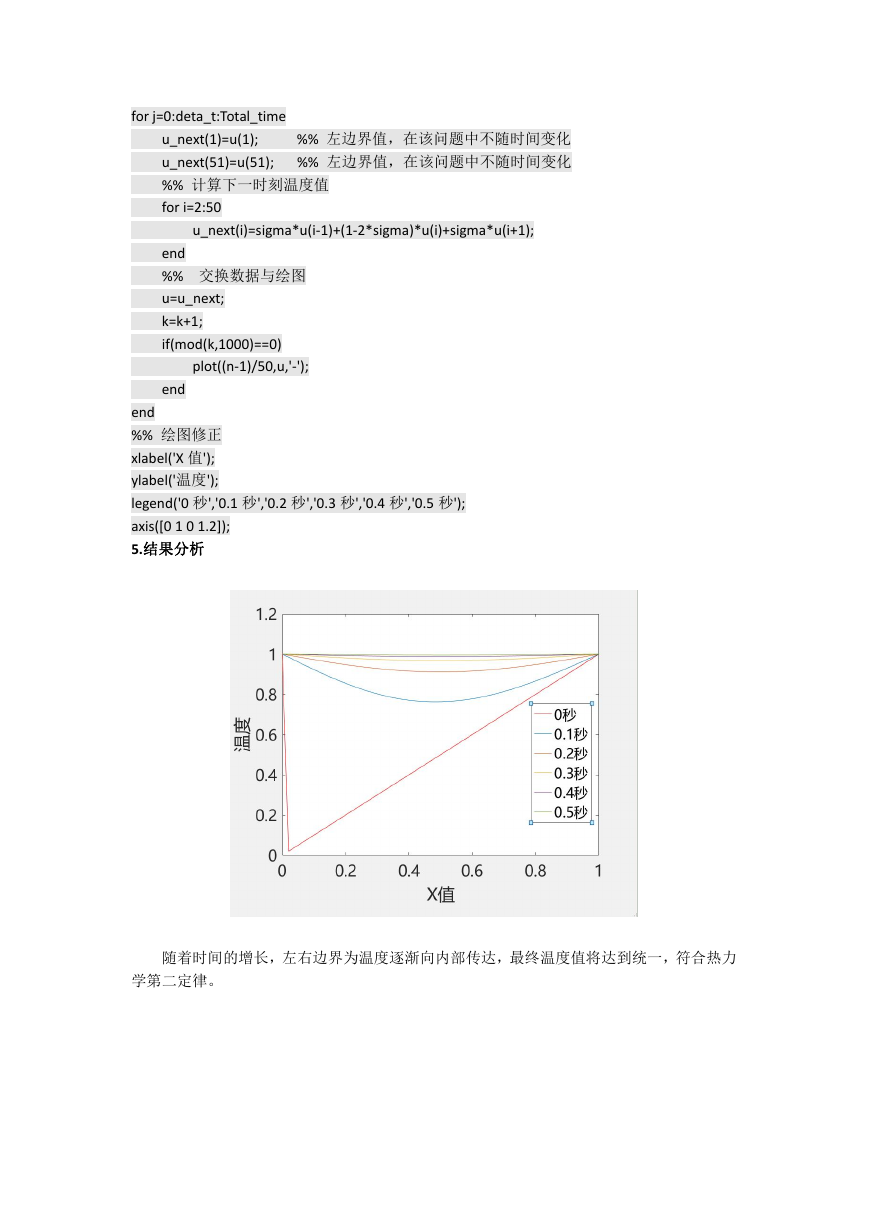
5.结果分析
随着时间的增长，左右边界为温度逐渐向内部传达，最终温度值将达到统一，符合热力
学第二定律。
2.弦的无阻尼自由振动方程
22=222
其中，t 是时间，x 是横坐标，u 是弦的横向位移;
=,T 是弦上的纵向张力，ρ是弦的线密度
1.为便于求解，给定如下边值条件=0,=1,=1,=1
>0 边值
,=0=cos(2)
0<<1 初场
0<<1
,=0=0
2.为便于求解令=，令,为横坐标节点数和时间节点数
，∆为时间间隔。
时间项 使用向前差分，即=,+−,+,−
∆
，∆为空间间隔。
空间项使用二阶中心差分，即=+,−,+−,
∆
原式可变为 ,+−,+,−
=+,−,+−,
∆
∆
,+=∆∆+,+ −∆∆ ,+∆∆−,−,−
移项和整理成如下形式
注意：在=时刻，即=时，,−=,−，因为,=0=,−,−
所以,−=,，,==,−,
3.按稳定性条件∆∆<,所以取时间间隔∆=0.001s,空间间隔∆=0.02
∆ 。,=(∆∆+,+ −∆∆ ,+∆∆−,)，这
∆ =0，
一步仅在起始步有作用。
%% 左边值
%% 右边值
4.Matlab 编程如下
%% 给定边值，时间间隔，空间间隔,稳定性条件
u_a=1;
u_b=1;
deta_t=0.001; %% 时间间隔
Total_time=0.25; %% 总时长
deta_x=0.02;
n=1:51;
nn=max(n-1);
sigma=(deta_t^2)/(deta_x^2);
k=0;
%% 一维杆的初值
u(1)=u_a;
%% 空间间隔
%% 节点序号
%% 最大步数减一
%% 时刻标志位，用于绘图
%% 左边值
u(nn+1)=u_b;
for i=2:nn
%% 右边值
u(i)=cos(2*pi*(i-1)/nn);
%% 初始时刻的函数
%% 画出初始时刻位移图
end
plot((n-1)/nn,u,'ro');
hold on
%% 起始步
u_next(1)=u(1);
u_next(nn+1)=u(nn+1);
%% 左边界值，在该问题中不随时间变化
%% 左边界值，在该问题中不随时间变化
%% 计算第一时刻位置值
for i=2:nn
u_next(i)=0.5*(sigma*u(i+1)+(2-2*sigma)*u(i)+sigma*u(i-1));
end
u_last=u;
u=u_next;
k=k+1;
plot((n-1)/nn,u,'b+');
%% 时间步进
for j=deta_t:deta_t:Total_time
%% 画出起始步时刻位移图
%% 左边界值，在该问题中不随时间变化
%% 左边界值，在该问题中不随时间变化
u_next(1)=u(1);
u_next(nn+1)=u(nn+1);
%% 计算下一时刻位移值
for i=2:nn
u_next(i)=sigma*u(i+1)+(2-2*sigma)*u(i)+sigma*u(i-1)-u_last(i);
end
%% 交换数据与绘图
u_last=u;
u=u_next;
k=k+1;
if(mod(k,50)==0)
plot((n-1)/nn,u,'-');
end
end
%% 绘图修正
xlabel('X 值');
ylabel('位移');
legend('0 秒','0.001 秒','0.05 秒','0.10 秒','0.15 秒','0.20 秒','0.25 秒');
axis([0 1 -1 1]);
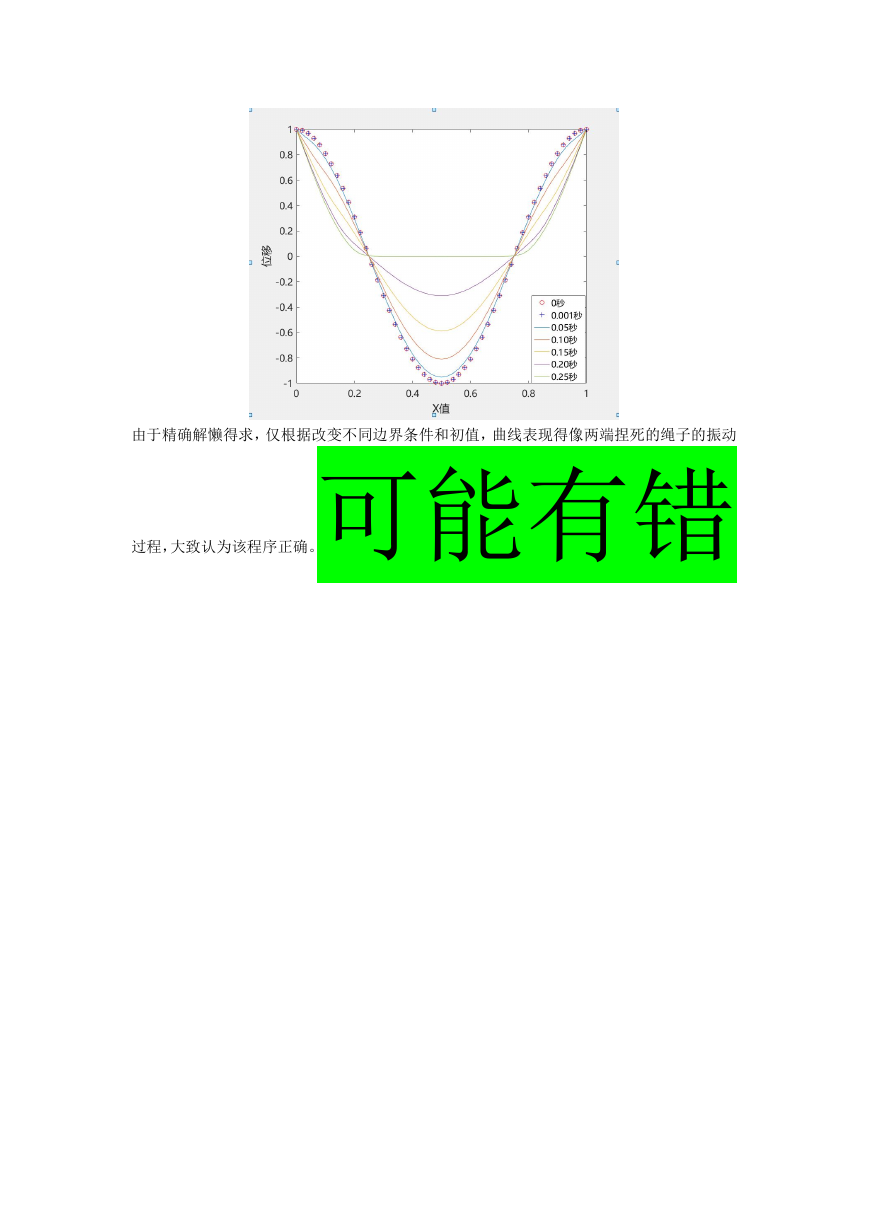
5.结果分析
由于精确解懒得求，仅根据改变不同边界条件和初值，曲线表现得像两端捏死的绳子的振动
过程，大致认为该程序正确。可能有错
3.拉普拉斯方程（常用于稳态引力场 稳态静电场 稳态温度场）
22+22=0
1.为便于求解，给定如下边值条件
其中，x 是横坐标，y 是纵坐标，u 是稳定的温度;
∈ , 边值
=0,=1,=1,=0
∈ , 边值
,=0=1,,=1=1
2.为便于求解令=，令,为横坐标节点数和纵坐标节点数
空间项使用二阶中心差分，即=+,−,+−,
∆
空间项使用二阶中心差分，即=,+−,+,−
∆
=
原式可变为 +,−,+−,
∆
∆+∆ +,+ −, + ∆
,= ∆
−,+−,+,−
∆
移项和整理成如下形式
，∆为空间向间隔。
，∆为空间向间隔。
∆+∆( ,++ ,−)
由于直接求解矩阵较大，为便于迭代，采用超松弛迭代，迭代的顺序是逐行迭代，如下图，
蓝色是边界值不参与迭代，迭代顺序是 a->b->c->d->e->f->g->h->l (i 已使用，跳过)
即将上述公式转为：
∆
∆
+
∆+∆ +,
,+=
,+
∆+∆
∆
∆
∆+∆ ,−+ +(−),
+ +
+
∆+∆ −,
其中，是超松弛因子， 最佳超松弛因子由如下公式确定：
2
ω=
max−1+cos
max−1
1+ 1− cos
2
3.为便于求解,取空间间隔∆=0.01,空间间隔∆=0.01，,∈ ,
2
%% y 间隔
%% 节点序号
4.Matlab 编程如下
%% 给定空间区域，空间间隔,超松弛因子
deta_x=0.01; %% x 间隔
Total_x=1; %% 总 x 长
deta_y=0.01;
Total_y=1; %% 总 y 长
n=1:((Total_x/deta_x)+1);
nn=max(n)-1;
sigma=0.25;
omega=2/(1+sqrt(1- ((cos(pi/nn)+cos(pi/nn))/2 ).^2) ); %% 最佳超松弛因子
iteration_max=10000;
convergence=1e-8;
%% 二维温度场的坐标值和初值
for i=1:nn
%迭代总次数
%迭代精度
x(i)=i*deta_x; %% 定义网格点坐标
end
for j=1:nn
y(j)=j*deta_y; %% 定义网格点坐标
end
u=zeros(nn,nn); %对 u 赋初值
%% 二维温度场的四条边的边界值
for i=1:nn
j=1;
u(i,j)=1;
%% y=0 的 u 值
end
for i=1:nn
j=nn;
u(i,j)=0;
end
for j=1:nn
i=1;
u(i,j)=1;
end
for j=1:nn
i=nn;
u(i,j)=1;
%% y=1 的 u 值
%% x=0 的 u 值
%% x=1 的 u 值
end
u_last=u;
u_next=u;
%% 设置迭代
for iteration=1:iteration_max
for j=2:nn-1
for i=2:nn-1
u_next(i,j)=omega.*sigma.*(u(i+1,j)+u(i,j+1)+u(i-1,j)+u(i,j-1))...
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
