logo资料库

数字图像处理实验报告.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：1.38M 资料格式：docx 举报 版权申诉
第1页 / 共17页
第2页 / 共17页
第3页 / 共17页
第4页 / 共17页
第5页 / 共17页
第6页 / 共17页
第7页 / 共17页
第8页 / 共17页
资料共17页，剩余部分请下载后查看
    实验一 图像几何变换
    实验二 图像增强
    实验三 图像恢复
    实验四 图像边缘检测
    实验五 图像分割
    实验六 基于特征的图像识别
    实验一 图像几何变换 一、 实验目的 1. 掌握图像的基本几何变换的方法 2. 图像的平移 3. 图像的旋转 二、 实验内容 练习用 matalb 命令实现图像的平移、旋转操作。 1. 编写实现图像平移的函数。 2. 用 imread 命令从你的硬盘读取一幅 256×256 灰度图。 3. 调用平移函数，将 256×256 灰度图平移 100 行 200 列，在同一个窗口中 显示平移前和平移后的图像。 4. 再开辟一个窗口，分别用最近邻插值法、双线性插值法实现图像顺势针 旋转 50°，显示在同一窗口中，并比较两种效果图（在报告中）。 三、 实验算法分析 1. 图像平移算法： 2. 图像旋转算法： 四、 实验步骤 利用 Matlab 编程，从硬盘中读取一张图片，然后实现图像的平移算法和旋 转算法，保存结果并截图。 五、 源程序 1. 图像平移 SY1shift.m clc %清空命令窗口 I=rgb2gray(imread('C:\Users\Zhilong\Pictures\SavedPictures\1.JPG'));% 读 入 图 片 并 转化为灰度图 subplot(1,2,1) imshow(I);%建立窗口，显示灰度图 I [r,c]=size(I);%计算灰度图的大小，r 表示行，c 表示列，即通过 size 函数将灰度图 I 的行数存在矩阵的 r 中，列数存在矩阵的 c 中，这样就知道灰度图的大小是 r
    ×c dst=zeros(r,c);%建立 r×c 的 0 矩阵（平移结果矩阵），初始化为零（黑色） dx=50;%平移的 x 方向的距离，这里是竖直方向 dy=80;%平移的 y 方向的距离，这里是水平方向 tras=[10dx;01dy;001];%平移变换矩阵 fori=1:r forj=1:c temp=[i;j;1];%灰度图 I 要平移变换的点，这里用矩阵表示 temp=tras*temp;%矩阵相乘，得到三行一列的矩阵 temp，即平移后的矩阵 x=temp(1,1);%把矩阵 temp 的第一行第一列的元素给 x y=temp(2,1);%把矩阵 temp 的第二行第一列的元素给 y if(x>=1&&x<=r)&&(y>=1&&y<=c)%判断所变换后得到的点是否越界 dst(x,y)=I(i,j);%得到平移结果矩阵，点(x,y)是由点(i,j)平移而来的，有对应关系 end end end subplot(1,2,2) imshow(uint8(dst));%建立窗口，显示平移后的图 2. 图像旋转 SY1rotation.m init=imread('C:\Users\Zhilong\Pictures\SavedPictures\1.JPG');%读取图像 subplot(2,1,1) imshow(init);%建立窗口，显示灰度图 I [R,C]=size(init);%获取图像大小 res=zeros(R,C);%构造结果矩阵。每个像素点默认初始化为 0（黑色） alfa=-30*3.1415926/180.0;%旋转角度 tras=[cos(alfa)-sin(alfa)0;sin(alfa)cos(alfa)0;001];%旋转的变换矩阵 fori=1:R forj=1:C temp=[i;j;1]; temp=tras*temp;%矩阵乘法 x=uint16(temp(1,1)); y=uint16(temp(2,1)); %变换后的位置判断是否越界 if(x<=R)&(y<=C)&(x>=1)&(y>=1) res(i,j)=init(x,y); end end end; subplot(2,1,2) imshow(uint8(res));%显示图像 六、 实验结果
    1. 图像平移 2. 图像旋转 七、 结果分析和讨论 本实验根据图像像素点坐标的变换，实现了对图像的平移操作和旋转操作。 用 matlab 的库函数读取图像后，要转换为了二值图，并计算图像的大小，利用 矩阵的加减乘除运算，变换像素点的坐标，从而组建得到新的图像。
    实验二 图像增强 一、 实验目的 熟悉数字图像增强的一般方法，包括： 1. 掌握空域变换增强的原理、方法。 2. 掌握直方图变换的原理、方法。 二、 实验内容 练习图像增强的 Matlab 命令：histeq，histem。 1. 一幅 256X256 的灰度图像如图（a）,将 0~60 灰度级压缩到 0~30 范围内, 压缩比 1/2;60~180 的灰度级扩大到 30~240,比率为 190/120;将 180~255 灰度级压 缩到 240~255 范围内,压缩比为 15/75。 2. 熟悉命令 histeq，将原图做直方图均衡处理，比较图像增强的效果，并 用命令 histem 绘制增强后图像的直方图。 三、 实验算法分析 直方图是一个统计数据，变现为图像中灰度值出现的概率，假设一副 640*480 的图像，其中灰度值为 100 的像素点为 1240 个，那么灰度值 100 出现 的概率为：1240/（640*480）.把每一个像素值出现的次数都统计出来，就得到 了各个值对应的概率。在这里加入一点概率分布和概率密度函数的记录，方便查 阅。设离散型随机变量 X 的分布律为: 四、 实验步骤 利用 matlab 编程从硬盘中读取图像，并将图像转为二维的，即灰值化。然 后调用 matlab 库函数 imshow 显示原始图像，imhist 显示图像的直方图，对图像 进行均衡化后，在显示出增强后的图像。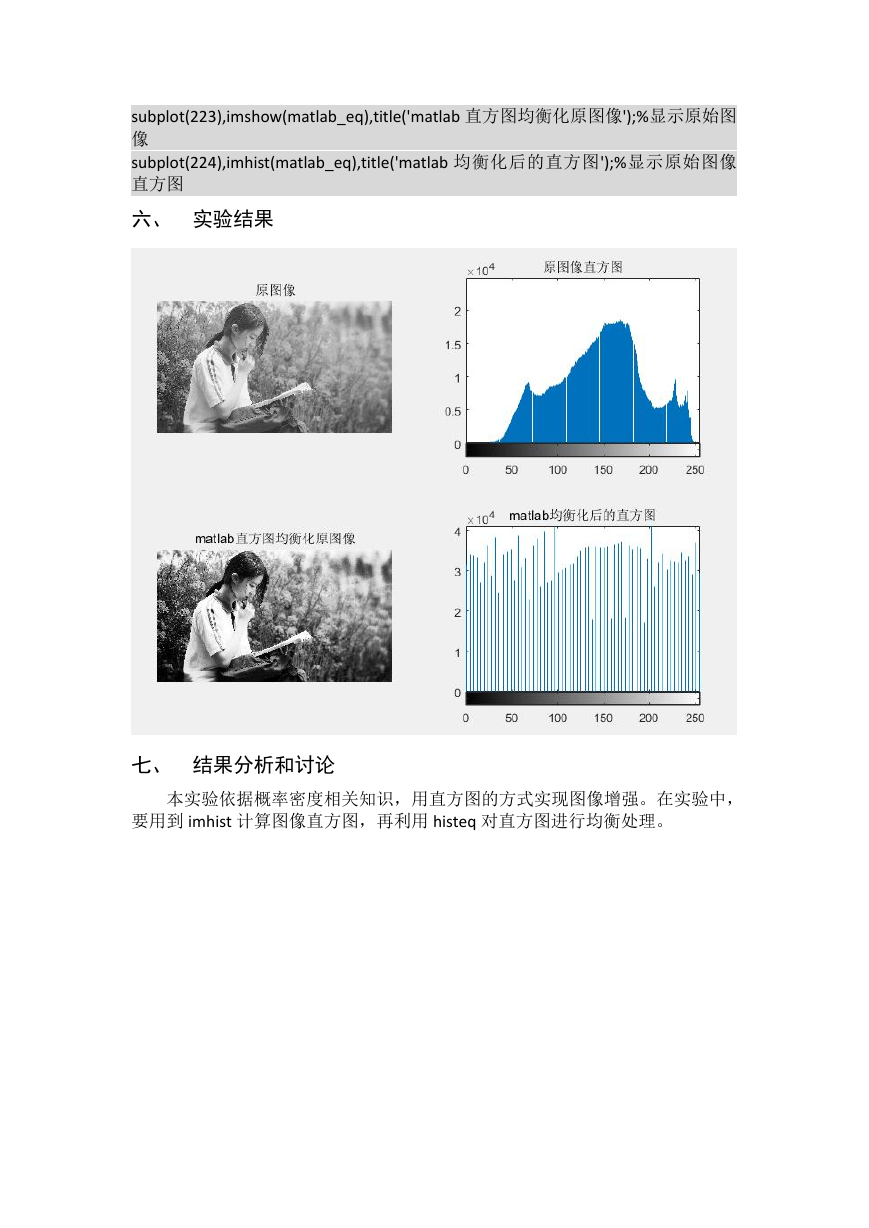 五、 源程序 SY2.m clc,clear; src_img=imread('C:\Users\Zhilong\Pictures\SavedPictures\1.JPG'); src_img=rgb2gray(src_img);%灰值化 figure(1) subplot(221),imshow(src_img),title('原图像');%显示原始图像 subplot(222),imhist(src_img),title('原图像直方图');%显示原始图像直方图 matlab_eq=histeq(src_img);%利用 matlab 的函数直方图均衡化
    subplot(223),imshow(matlab_eq),title('matlab 直方图均衡化原图像');%显示原始图 像 subplot(224),imhist(matlab_eq),title('matlab 均衡化后的直方图');%显示原始图像 直方图 六、 实验结果 七、 结果分析和讨论 本实验依据概率密度相关知识，用直方图的方式实现图像增强。在实验中， 要用到 imhist 计算图像直方图，再利用 histeq 对直方图进行均衡处理。
    实验三 图像恢复 一、 实验目的 掌握图像恢复的常用方法：图像的几何畸变复原或者几何畸变校正。 二、 实验内容 对一幅硬盘中的图片进行几何畸变校正。 三、 实验算法分析 几何基准图像的坐标系统用(x,y)来表示，需要校正的图像的坐标系统用 (x’,y’)表示，设两个图像坐标系统之间的关系用解析式表示 通常 h1(x,y)和 h2(x,y)用多项式来表示： 通常用线性畸变来近似较小的几何畸变 更精确一些可以用二次型来近似 若基准图像为 f(x,y)，畸变图像为 g(x’,y’)，对于景物上的同一个点，假定 其灰度不变，则 已知 h1(x,y)和 h2(x,y) 通常用线性畸变来近似较小的几何畸变 零级内插 双线性插值 则：
    线性畸变 可 由 基 准 图 找 出 三 个 点 (r1,s1),(r2,s2),(r3,s3) 与 畸 变 图 像 上 三 个 点 (u1,v1),(u2,v2),(u3,v3)一一对应。 将对应点代入，有： 解联立方程组，得出 6 个系数。  四、 实验步骤 利用 matlab 编程从硬盘中读取图像，图像坐标系和矩阵的表示是相反的， 将图像像素点 x 和 y 进行畸变的处理，再利用线性插值得到非畸变的图像，与畸 变图像进行对比。 五、 源程序 SY3.m clear; clc; A=[5.9418398977142772e+00203.1950000000000000e+002; 05.941839897714e+0022.3950000000000000e+002; 001]; D=[6.7442695842244271e-0022.4180872220967919e-00100-3.3970575589699975e -001]; fx=A(1,1); fy=A(2,2); cx=A(1,3); cy=A(2,3); k1=D(1); k2=D(2); k3=D(5); p1=D(3); p2=D(4);
    K=A; I_d=imread('C:\Users\Zhilong\Pictures\SavedPictures\1.JPG'); I_d=rgb2gray(I_d); I_d=im2double(I_d); I_r=zeros(size(I_d)); %图像坐标系和矩阵的表示是相反的 %[row,col]=find(X)，坐标按照列的顺序排列，这样好和 reshape()匹配出响应的图 像矩阵 [vu]=find(~isnan(I_r)); %XYZc 摄像机坐标系的值，但是已经归一化了，因为没有乘比例因子 %公式 s[uv1]'=A*[XcYcZc]'，其中 s 为比例因子，不加比例因子，Zc 就为 1，所以 此时的 Xc 相对于(Xc/Zc) XYZc=inv(A)*[uvones(length(u),1)]'; %此时的 x 和 y 是没有畸变的 r2=XYZc(1,:).^2+XYZc(2,:).^2; x=XYZc(1,:); y=XYZc(2,:); %x 和 y 进行畸变的 x=x.*(1+k1*r2+k2*r2.^2)+2*p1.*x.*y+p2*(r2+2*x.^2); y=y.*(1+k1*r2+k2*r2.^2)+2*p2.*x.*y+p1*(r2+2*y.^2); %(u,v)对应的畸变坐标(u_d,v_d) u_d=reshape(fx*x+cx,size(I_r)); v_d=reshape(fy*y+cy,size(I_r)); %线性插值出非畸变的图像 I_r=interp2(I_d,u_d,v_d); %对比图像 subplot(121); imagesc(I_d); title('畸变原图像'); subplot(122); imagesc(I_r); title('校正后图像'); 六、 实验结果
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料