和利时/Hollysys_ConMaker组态手册_附录：自整定PID的使用.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：1.08M 资料格式：pdf 举报版权申诉

weixin_38743481-11859411-4744302542950134876.pdf-第1页.png

第1页 / 共9页

weixin_38743481-11859411-4744302542950134876.pdf-第2页.png

第2页 / 共9页

weixin_38743481-11859411-4744302542950134876.pdf-第3页.png

第3页 / 共9页

weixin_38743481-11859411-4744302542950134876.pdf-第4页.png

第4页 / 共9页

weixin_38743481-11859411-4744302542950134876.pdf-第5页.png

第5页 / 共9页

weixin_38743481-11859411-4744302542950134876.pdf-第6页.png

第6页 / 共9页

weixin_38743481-11859411-4744302542950134876.pdf-第7页.png

第7页 / 共9页

weixin_38743481-11859411-4744302542950134876.pdf-第8页.png

第8页 / 共9页

文本预览

SmartPro 自整定 PID 的使用 1. 自整定原理简介.................................................................................................................................................................2 2. 自整定方法简介.................................................................................................................................................................2 3. 自整定 PID 相关参数定义...............................................................................................................................................2 4. 自整定 PID 使用 ................................................................................................................................................................2 5. 注意事项 ..............................................................................................................................................................................3 6. 实际使用仿真 .....................................................................................................................................................................4 6.1 采样周期 0.1 S.........................................................................................................................................................4 6.2 采样周期 0.5 S.........................................................................................................................................................7 7. 推荐.......................................................................................................................................................................................9 第 1 页共 9 页

1. 自整定原理简介在自整定方式下，调节器的输出产生震荡，以方波、正玄波常见。此时对象反馈相应震荡，对象特性可以计算出来，再由此产生调节器参数。在 SmartPro 的 hsac.lib 库中的 HSPIDITG 功能块中，集成了自整定 PID。 2. 自整定方法简介，缺省值目前可以使用的 PID 自整定方法（tunning mode）有： 1． Ziegler-Nichols PI 2． Ziegler-Nichols PID 3． Astron-Hannlund PID 4． Wang Adam PI 5． Wang Adam PID 6． Gain-phase Margin PID 7． Robust Optimal PI 8． Sensitivity Optimal PI 此自整定方法可以设定，tunning mode 为 BYTE 类型，如设定为其它值（1— 8 以外），则使用缺省值 2，即 Ziegler-Nichols PID 工作方式。 3. 自整定 PID 相关参数定义 relay ：REAL auto_pt:REAL auto_ti:REAL auto_td:REAL; accptautopara:BOOL; 确认接受 pid 自整定参数输出振幅 pid 自整定计算参数：比例带 pid 自整定计算参数：积分时间 pid 自整定计算参数：微分时间 4. 自整定 PID 使用如下使用，均在 ConMaker 的 HSPIDITG(或 HSART_PID1)类型的功能块中进行。 1）将 PID 置为手动（RM=0），调整输出至现场的正常工作点上。一般应以50 附近为宜。主要考虑到在自整定过程中，输出震荡，必须预留足够的震荡空间，否则对象反馈可能不起震，自整定方法失败。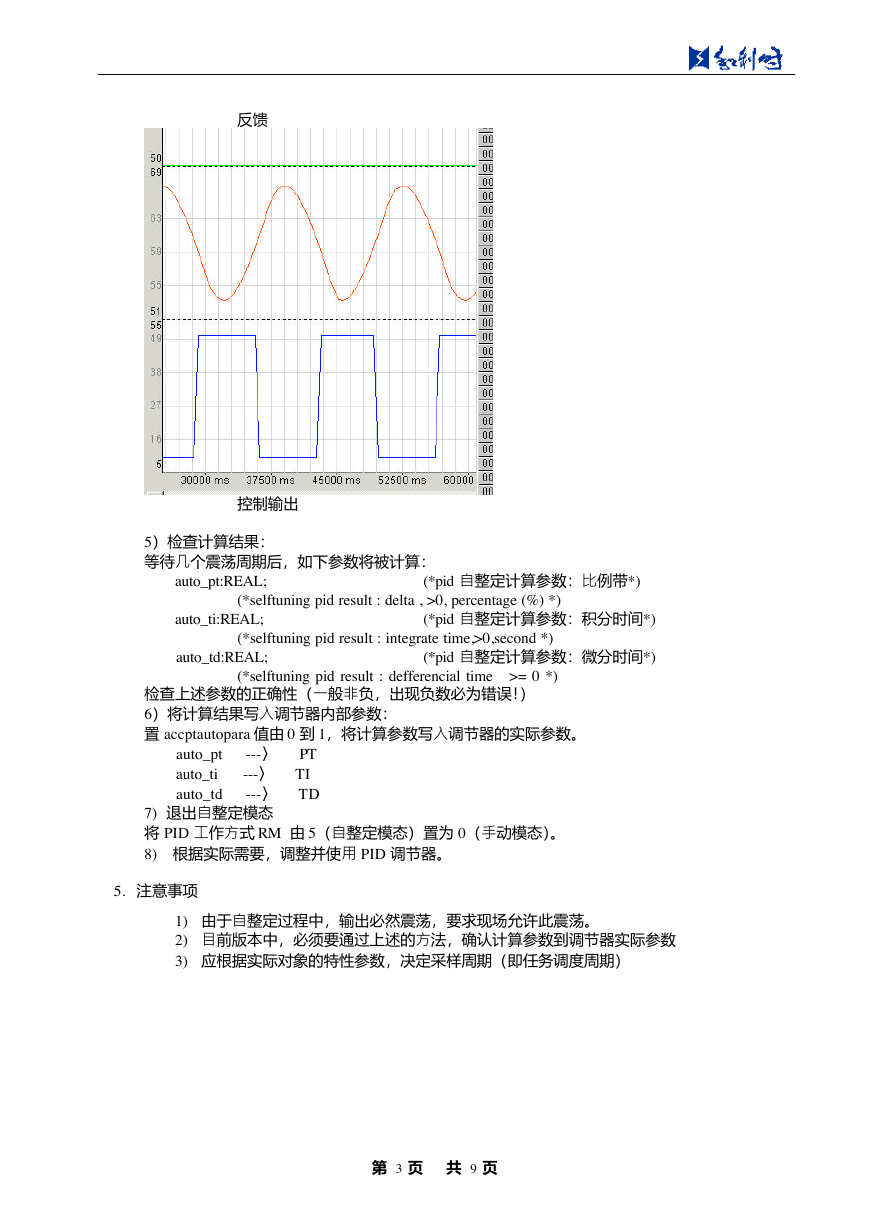 2）设定 PID 的 RM 值为 5，进入自整定模态 3）选择设定 PID 的 tunning mode，设定自整定方法 4）此时调节输出应震荡，参看下图：第 2 页共 9 页

反馈控制输出 5）检查计算结果：等待几个震荡周期后，如下参数将被计算： (*selftuning pid result : delta , >0, percentage (%) *) (*pid 自整定计算参数：比例带*) (*selftuning pid result : integrate time,>0,second *) (*pid 自整定计算参数：积分时间*) (*pid 自整定计算参数：微分时间*) auto_pt:REAL; auto_ti:REAL; auto_td:REAL; (*selftuning pid result : defferencial time >= 0 *) 检查上述参数的正确性（一般非负，出现负数必为错误！） 6）将计算结果写入调节器内部参数：置 accptautopara 值由 0 到 1，将计算参数写入调节器的实际参数。 auto_pt ---〉 PT auto_ti ---〉 TI auto_td ---〉 TD 7) 退出自整定模态将 PID 工作方式 RM 由 5（自整定模态）置为 0（手动模态）。 8) 根据实际需要，调整并使用 PID 调节器。 5. 注意事项 1) 由于自整定过程中，输出必然震荡，要求现场允许此震荡。 2) 目前版本中，必须要通过上述的方法，确认计算参数到调节器实际参数 3) 应根据实际对象的特性参数，决定采样周期（即任务调度周期）第 3 页共 9 页

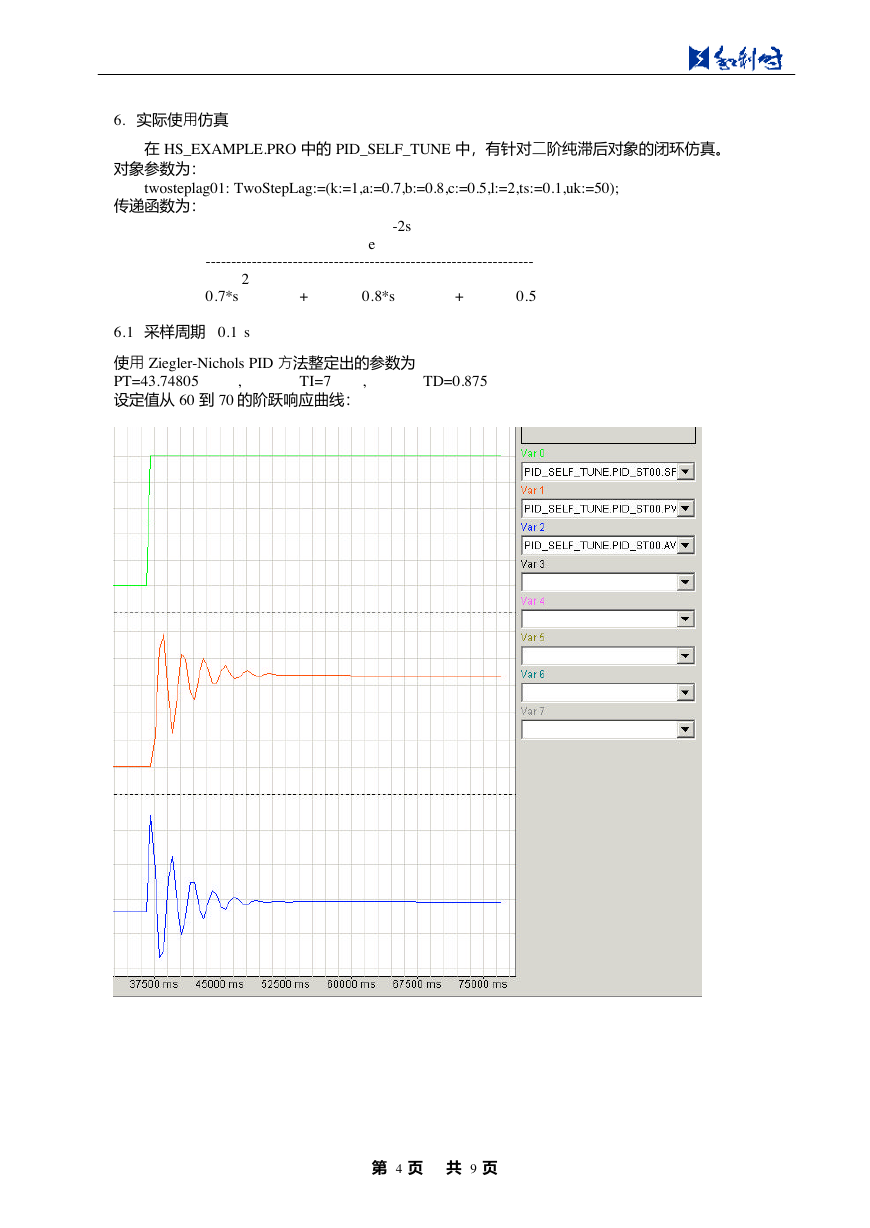
6. 实际使用仿真在 HS_EXAMPLE.PRO 中的 PID_SELF_TUNE 中，有针对二阶纯滞后对象的闭环仿真。对象参数为： twosteplag01: TwoStepLag:=(k:=1,a:=0.7,b:=0.8,c:=0.5,l:=2,ts:=0.1,uk:=50); 传递函数为： -2s e ---------------------------------------------------------------- 2 0.7*s + 0.8*s + 0.5 6.1 采样周期 0.1 s 使用 Ziegler-Nichols PID 方法整定出的参数为 PT=43.74805 设定值从 60 到 70 的阶跃响应曲线： TI=7 , , TD=0.875 第 4 页共 9 页

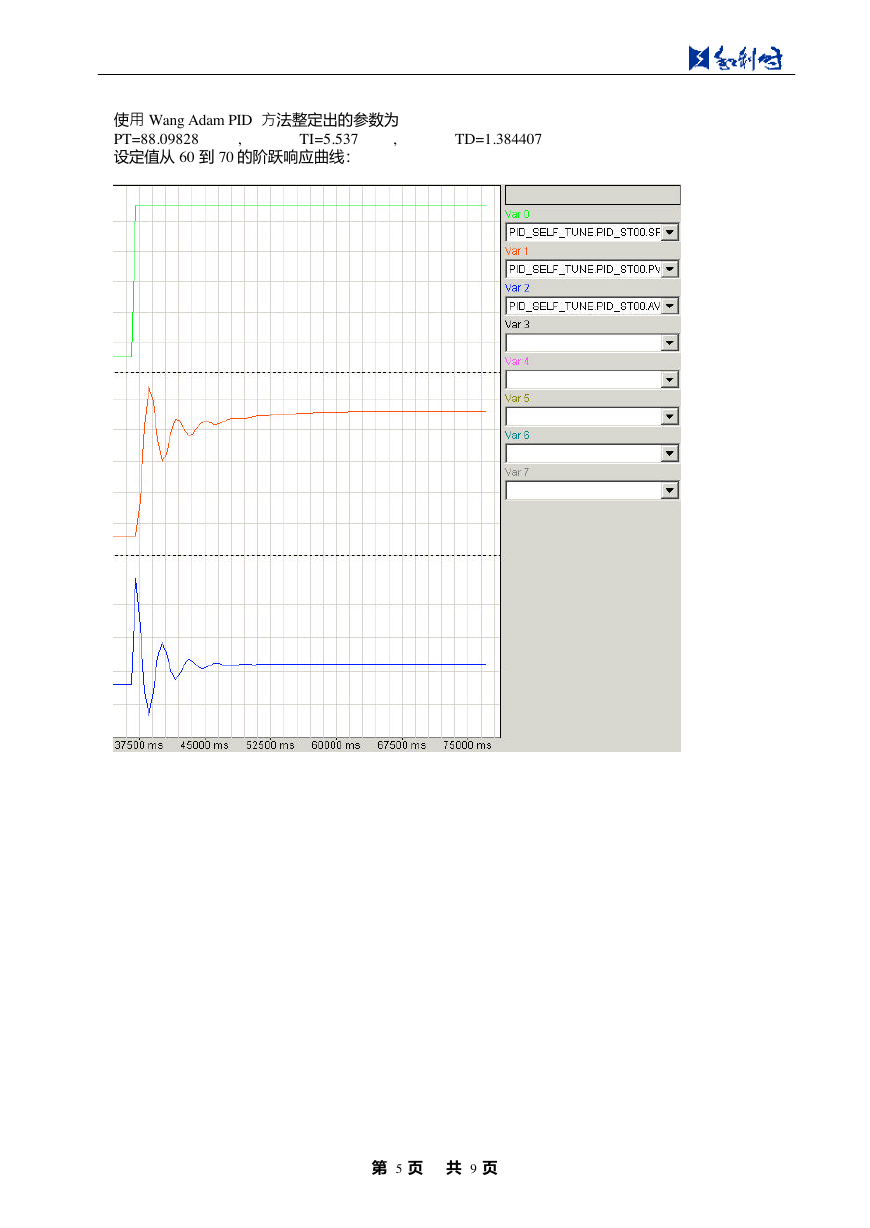
使用 Wang Adam PID 方法整定出的参数为 PT=88.09828 , TI=5.537 设定值从 60 到 70 的阶跃响应曲线： , TD=1.384407 第 5 页共 9 页

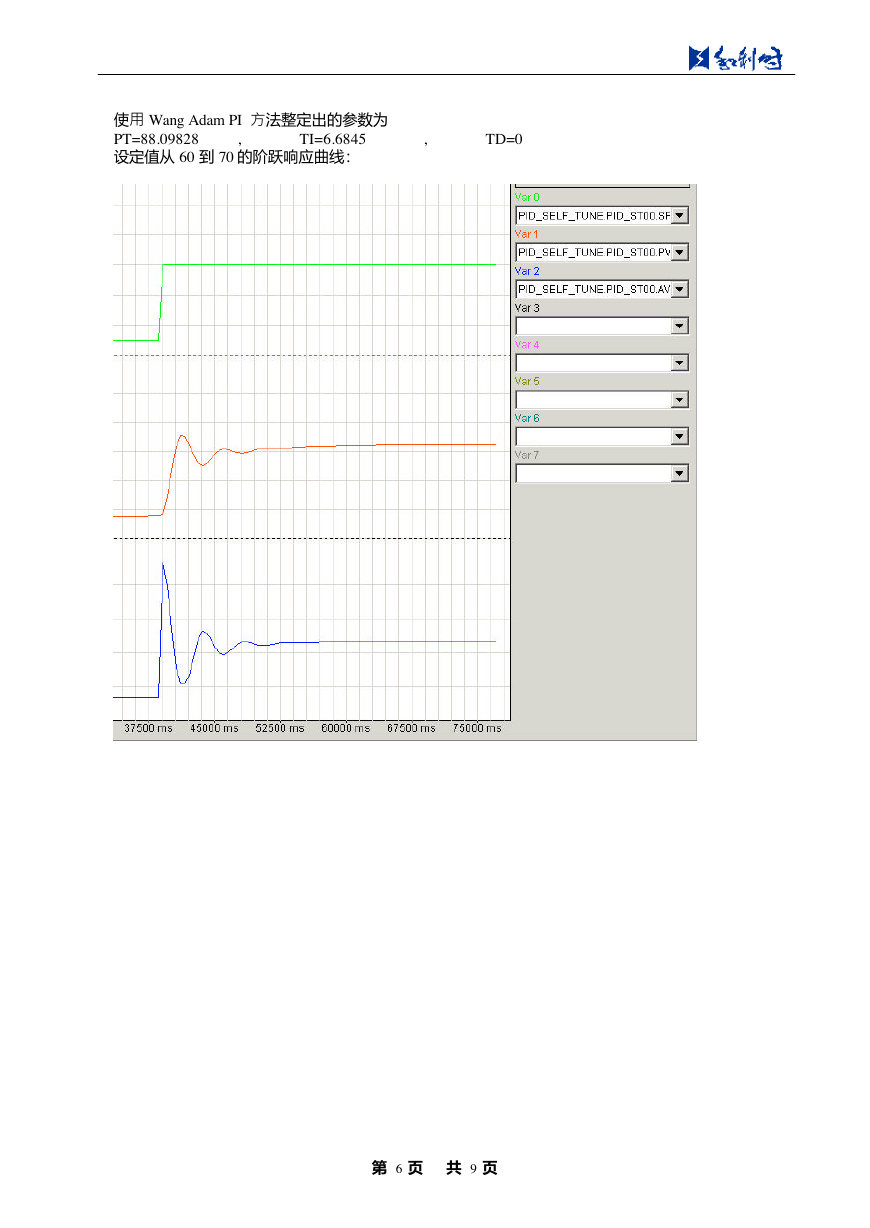
使用 Wang Adam PI 方法整定出的参数为 PT=88.09828 TI=6.6845 设定值从 60 到 70 的阶跃响应曲线： , , TD=0 第 6 页共 9 页

6.2 采样周期 0.5 s 使用 Ziegler-Nichols PID 方法整定出的参数为 PT=150.5969 设定值从 60 到 70 的阶跃响应曲线： TI=3 , , TD=0.375 第 7 页共 9 页

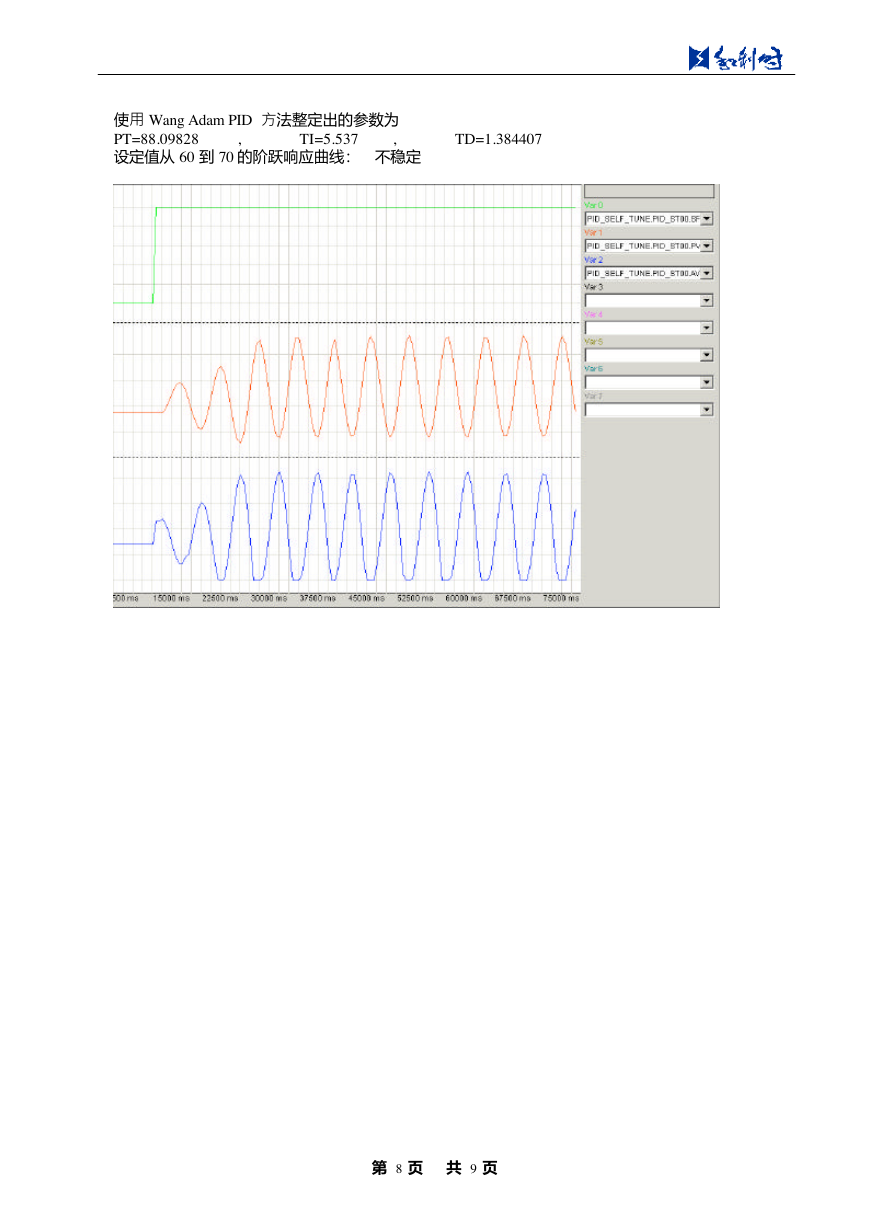
使用 Wang Adam PID 方法整定出的参数为 PT=88.09828 , 设定值从 60 到 70 的阶跃响应曲线：不稳定 TI=5.537 , TD=1.384407 第 8 页共 9 页

分享到：

赞收藏

资料库

和利时/Hollysys_ConMaker组态手册_附录：自整定PID的使用.pdf

相关推荐

开发技术

热门标签

最新资料