logo资料库

背包问题实验报告.doc

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.08M 资料格式：doc 举报 版权申诉
第1页 / 共10页
第2页 / 共10页
第3页 / 共10页
第4页 / 共10页
第5页 / 共10页
第6页 / 共10页
第7页 / 共10页
第8页 / 共10页
资料共10页，剩余部分请下载后查看
    实验题目：背包问题 背包问题 问题描述：假设有一个能装入总体积为 T 的背包和 n 件体积分别为 w1 , w2 , … , wn 的 物品，能否从 n 件物品中挑选若干件恰好装满背包，即使 w1 +w2 + … + wn=T，要求找 出所有满足上述条件的解。 例如：当 T=10，各件物品的体积{1，8，4，3，5，2}时，可找到下列 4 组解： （1，4，3，2） （1，4，5） （8，2） （3，5，2）。 概要设计： 采用栈数据结构，利用回溯法的设计思想来解决背包问题。 首先将物品排成一列，然后顺序选取物品装入背包，假设已选取了前 i 件物品之 后背包还没有装满，则继续选取第 i+1 件物品，若该件物品“太大”不能装入，则弃 之而继续选取下一件，直至背包装满为止。但如果在剩余的物品中找不到合适的物品以 填满背包，则说明“刚刚”装入背包的那件物品“不合适”，应将它取出“弃之一边”， 继续再从“它之后”的物品中选取，如此重复，直至求得满足条件的解，或者无解。 ADT Stack { 数据对象：D＝{ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 } 数据关系：R1＝{ | ai-1, ai∈D, i=2,...,n } 约定 an 端为栈顶，a1 端为栈底。 基本操作： InitStack(&S) 操作结果：构造一个空栈 S。 DestroyStack(&S) 初始条件：栈 S 已存在。 操作结果：栈 S 被销毁。 ClearStack(&S) 初始条件：栈 S 已存在。 操作结果：将 S 清为空栈。 StackEmpty(S) 初始条件：栈 S 已存在。
    操作结果：若栈 S 为空栈，则返回 TRUE，否则 FALSE。 StackLength(S) 初始条件：栈 S 已存在。 操作结果：返回 S 的元素个数，即栈的长度。 GetTop(S, &e) 初始条件：栈 S 已存在且非空。 操作结果：用 e 返回 S 的栈顶元素。 Push(&S, e) 初始条件：栈 S 已存在。 操作结果：插入元素 e 为新的栈顶元素。 Pop(&S, &e) 初始条件：栈 S 已存在且非空。 操作结果：删除 S 的栈顶元素，并用 e 返回其值。 } ADT Stack 源代码： #include #include #include #include #define OK 1 #define N 20 FILE *fp1,*fp2; //fp1 指向数据文件，fp2 指向结果文件 typedef struct SqStack{ int *base; int *top; int num;
    }SqStack; struct SqStack *S,L; int InitStack(SqStack *s,int n){ s->base=(int *)malloc(n*sizeof(int)); if(!s->base) exit(0); s->top=s->base; s->num=0; return OK; }//创建栈 int Push(SqStack *s,int m){ *s->top++=m; s->num++; return OK; }//元素入栈 int Pop(SqStack *s,int *p){ if(s->base==s->top)return 0; --s->top; *p=*s->top;
    s->num--; return OK; }//元素出栈,用指针 p 返回 int print(SqStack *s,int w[]){ int *p; p=s->base; while(ptop){ fprintf(fp2,"%d ",w[*p]); printf("%d ",w[*p]); p++; } fprintf(fp2,"\n"); printf("\n"); return OK; }//把栈中元素在文件中输出和在屏幕上输出 int StackEmpty(SqStack *s){ if(s->base==s->top) return 0; else return 1; }//栈是否为空
    void knapsack (int w[],int T,int n) { // 已知 n 件物品的体积分别为 w[0], w[1], …, w[n]，背包的总体积为 T, // 本算法输出所有恰好能装满背包的物品组合解 // 从第 0 件物品考察起 //计算输出结果组数，如果没有，则提示无结果 int k=0; int pint=0; int *pk=&k; S=&L; InitStack(S,n); do{ if(Pop(S,pk)){ // 退出栈顶物品 T+=w[k]; k++; // 继续考察下一件物品 } while(T>0&&k=0) { // 第 k 件物品可选，则 k 入栈 Push(S,k); T-=w[k]; } k++; // 继续考察下一件物品 if(T==0) {
    print(S,w); pint++; }// 输出第一组解 } } while ((StackEmpty(S))&&(k<=n)); if(!pint){ //while fprintf(fp2,”未找到匹配结果”); printf(“未找到匹配结果”); } }// knapsack int main(int argc,char *argv[]){ //命令输入为：(可执行文件名）（输入文件名）（输出文件名） //例如：beibao shuju.txt jieguo.txt //shuju.txt 文件中输入为：T n w1 w2 ... wn int i,n,T; int a[N]; if((fp1=fopen(argv[1],"r"))==NULL){ printf("文件未找到，请创建并输入:");
    exit(0); } if((fp2=fopen(argv[2],"w"))==NULL){ printf("创建文件失败"); exit(0); } fscanf(fp1,"%d%d",&T,&n); for(i=0;i
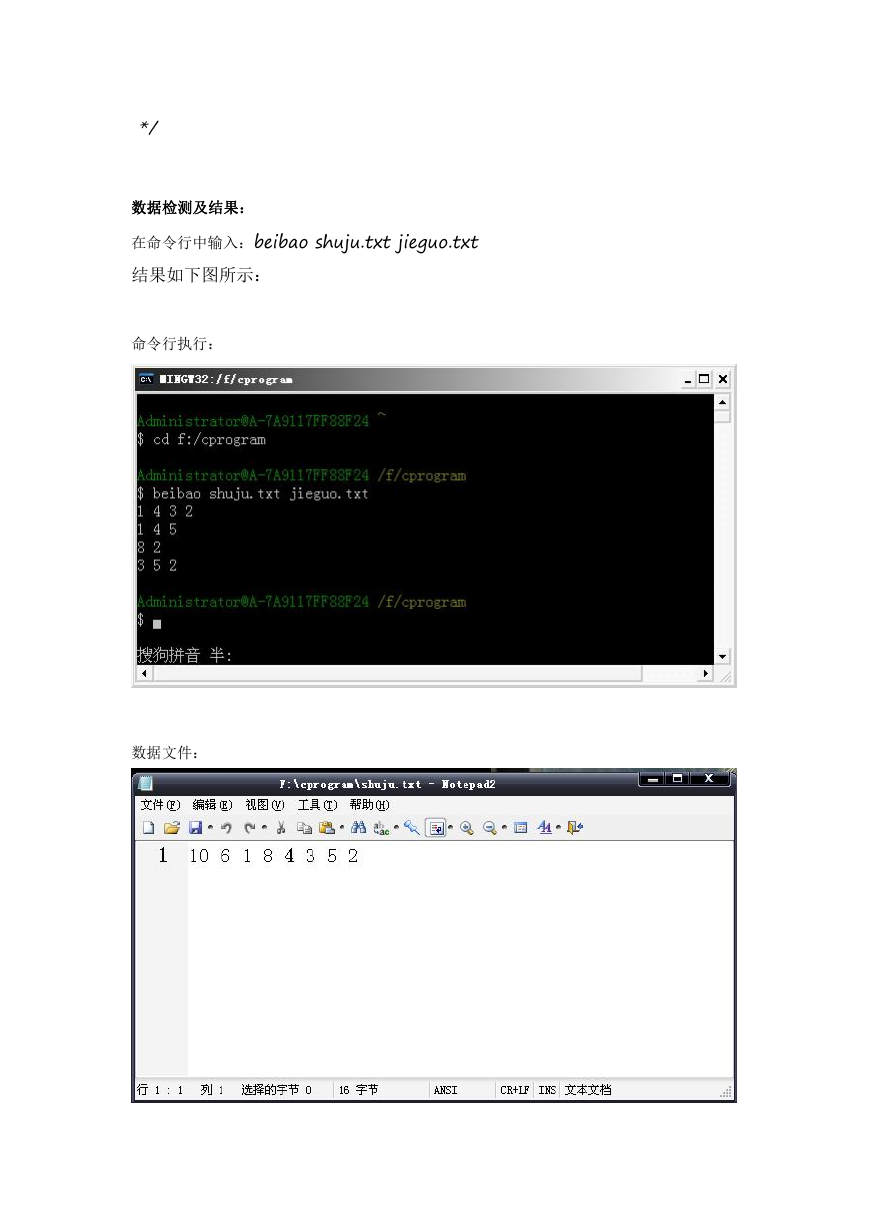
    */ 数据检测及结果： 在命令行中输入：beibao shuju.txt jieguo.txt 结果如下图所示： 命令行执行： 数据文件：
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料