论文研究-基于MATLAB的三维混沌系统吸引子的研究 .pdf-资料库

weixin_39840588-11570727-4744302542963558684.pdf-第1页.png

第1页 / 共7页

weixin_39840588-11570727-4744302542963558684.pdf-第2页.png

第2页 / 共7页

weixin_39840588-11570727-4744302542963558684.pdf-第3页.png

第3页 / 共7页

weixin_39840588-11570727-4744302542963558684.pdf-第4页.png

第4页 / 共7页

weixin_39840588-11570727-4744302542963558684.pdf-第5页.png

第5页 / 共7页

weixin_39840588-11570727-4744302542963558684.pdf-第6页.png

第6页 / 共7页

weixin_39840588-11570727-4744302542963558684.pdf-第7页.png

第7页 / 共7页

基于 MATLAB 的三维混沌系统吸引子的研究 http://www.paper.edu.cn 陈朝1，2 汤天浩1 沈鼎新1 1上海海事大学电气自动化系上海（200135） 2中国地质大学信息工程学院武汉（430074） chenzhao217@126.com 摘要混沌研究的复杂性大都源于其非线性，对于非线性方程的解很难给出具体的值，本文在试验仿真的基础上，实现了常见的 Chua’s 电路、Lorenz 系统和 Rossler 系统等三维混沌系统的吸引子仿真图形，在给出几种三维混沌系统的吸引子图形基础上分析其内在的联系。关键词混沌，吸引子，仿真 1. 引言分析复杂的非线性系统可用在相空间观察其轨道的方法。所谓相空间就是由所研究的物理量本身作为坐标分量所构成的广义空间，系统的任意状态相当于相空间中的一个代表点，系统的状态随时间变化过程对应于代表点在相空间中的变化。非线性系统随时间的演变将趋向于维数比原来相空间低的极限集合——吸引子。有关混沌研究的主要方法一般包括：Lyapunov指数，微分拓扑等。三维混沌系统由于是一组复杂的常微分方程，因此其数值解不具有直观性，为了更好的分析其时间向量和状态向量的特性，在 MATLAB环境中仿真具有直观、简单、灵活的特性。[1] 2. 四阶龙格－库塔（Runge-Kutta）原理对 dY dt = ,( YtF ) ，一般的解法可以表示为 Y n =+ 1 Y n ×+ YtDh , n ( n ) ：其中 n YtD , n ( ) 是动点在 t ( n t , 1+n ) 中的平均速度。设 nY 是精确的， tY ( ) =+ 1 n tY ( n + h ) = tY ( ) + tYh ( ′ ) + n n tYh 2 ( ′′ 2 ) + n tYh 3 ( ′′′ !3 ) n L+ 所以得到： YtD , n ( n tY ( n 1 + ) = tY ( ) n ) − h tY ( ′= ) + n tYh ( ′′ 2 ) + n tYh 2 ( ′′′ !3 ) + n + L h r 1 − r ! r )( Y t ( n ) + L 由此得到高阶的单步法。本课题得到上海市教委重点学科建设项目资助。 1

但是，往往右函数的高阶导数或者无法直接得到、或者计算太过复杂。所以实际的做法是：用 t [ n t , 1+n ] 区间中解曲线邻域的一些已知点函数值的线性组合来代替 ,( YtF ) 的导数，从而得到高阶的单步法公式。 Runge-Kutta 法的局部截断误差估计比较复杂，它和方法的阶数、方法的具体系数、待 http://www.paper.edu.cn =+ 1 Y n 2 K 2 + 2 K 3 + K ] 4 + 1 ( + Kh [ 6 YtF , ) n 1 2 1 2 Yh , n tF ( tF ( tF ( + + + n n n n Yh , n Yh , n + = = = = K 1 K ⎧ Y ⎪ n ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ K K 2 3 4 ) 1 ) 2 + Kh 2 Kh 2 hK + ) 3 解微分方程的性质、采用的步长等等因素相关。如果采用固定步长计算，局部误差会有比较大的波动。 3. MATLAB 实现基于Runge-Kutta法，MATLAB提供了求常微分方程数值解的函数，一般调用格式为： [2] [t,y]=ode23(‘fname’,tspan,y0) [t,y]=ode45(‘fname’,tspan,y0) 其中 fname 是定义的函数文件名，该函数文件必须返回一个列向量。tspan 形式为 [t0,tf]，y0 表示求解区间。是初始状态列向量。t 和 y 分别给出时间向量和相应的状态向量。这两个函数分别采用了二阶、三阶Runge-Kutta法和四阶、五阶Runge-Kutta法，并采用自适应变步长的求解方法，即当解的变化较慢时采用较大的步长，从而使得计算速度很快，当解的变化较快时步长会自动地变小，从而使得计算精度很高。在MATLAB中一般选用四阶的龙格库塔方法，它对步长自动选取，既减少计算量又适应精度要求。尽管采用四阶龙格库塔方法，但误差还是不可避免。实际上，除非步长非常小，否则截断误差通常是较严重的误差来源。对于大多数系统而言，随积分步数的增加其误差将逐步减小。但是混沌系统的一个显著特征就是对初始条件的极端敏感性，扰动将明显地改变 ,( YtF ) 的轨迹，使得附近的轨迹呈指数分离。绝大多数工程上感兴趣的系统都是结构稳定的，即在中一个小扰动将导致在其吸引子中也产生一个相应的 F 小扰动。而数值误差可看作是一种扰动，因此，对混沌吸引子的模拟在细节上可能和实际情况不完全相同，但它保持了吸引子的宏观形状。 2

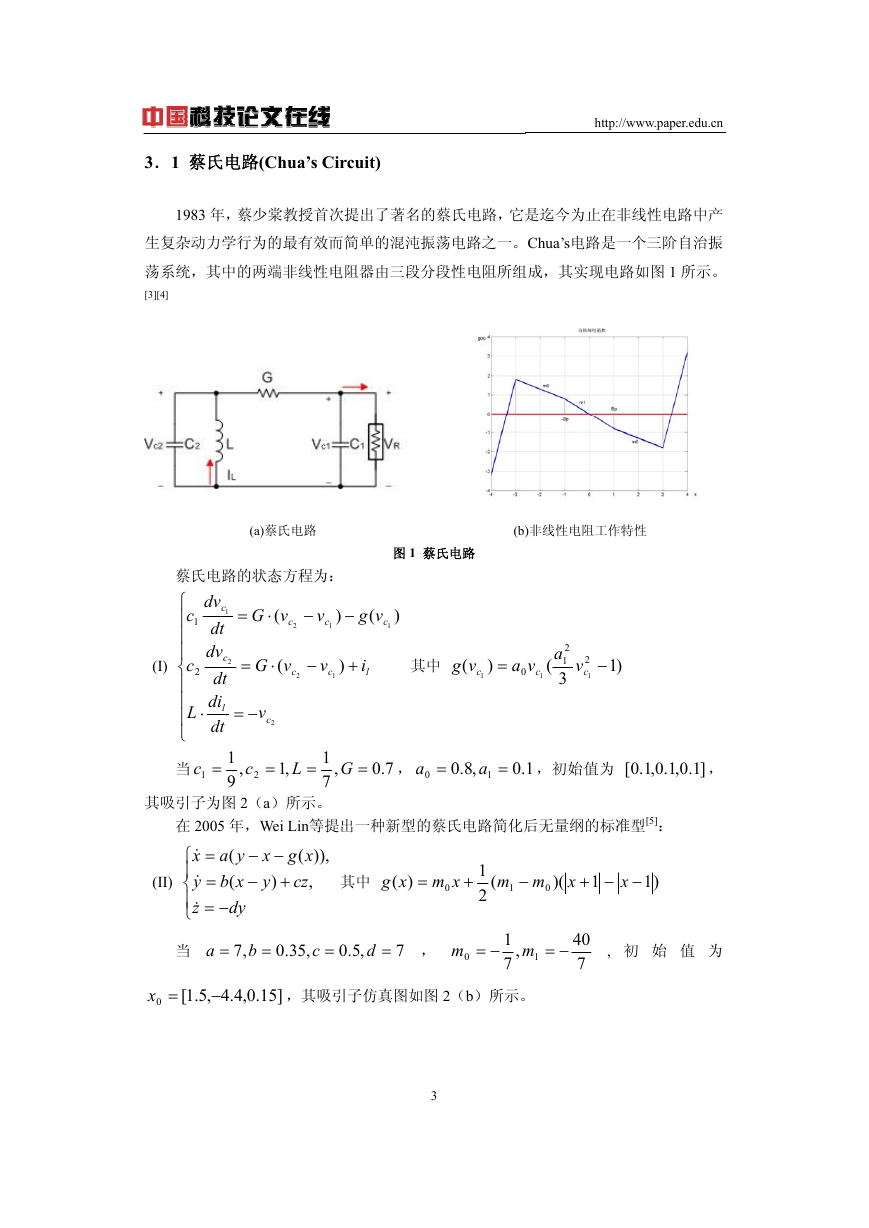
3．1 蔡氏电路(Chua’s Circuit) http://www.paper.edu.cn 1983 年，蔡少棠教授首次提出了著名的蔡氏电路，它是迄今为止在非线性电路中产生复杂动力学行为的最有效而简单的混沌振荡电路之一。Chua’s电路是一个三阶自治振荡系统，其中的两端非线性电阻器由三段分段性电阻所组成，其实现电路如图 1 所示。 [3][4] (a)蔡氏电路 (b)非线性电阻工作特性图 1 蔡氏电路 vg ( ) c 1 − + i l 其中 vg ( c 1 ) = va 0 c 1 ( va 2 1 3 2 c 1 − )1 c 2 ⋅ c 1 ) v = − vG ( 蔡氏电路的状态方程为： ⎧ c ⎪ 1 ⎪ ⎪ c ⎨ ⎪ ⎪ ⎪ ⎩ dv c 1 dt dv c dt di l dt vG ( −= L − = v v ) c 1 ⋅ ⋅ 2 c 2 c 2 (I) 2 当 c 1 1 7 其吸引子为图 2（a）所示。 1 9 ,1 L = = = c , 2 , G = 7.0 ， a 0 = ,8.0 a 1 = 1.0 ，初始值为 ]1.0,1.0,1.0[ ，在 2005 年，Wei Lin等提出一种新型的蔡氏电路简化后无量纲的标准型[5]： ⎧ ⎪ ⎨ ⎪ ⎩ xg ( −− cz ) , + − ya ( xb ( dy xmm )( = = −= −−+ 其中 xm 0 xg )( x & y & z & 1 2 x y )), )1 − + = 1 x ( 0 1 (II) 当 a = ,7 b = ,35.0 c = ,5.0 d = 7 ， m 0 −= 1 7 , m 1 −= 40 7 , 初始值为 =x 0 ]15.0,4.4,5.1[ − ，其吸引子仿真图如图 2（b）所示。 3

http://www.paper.edu.cn (a)离散蔡氏电路 (b)无量纲蔡氏电路图 2 蔡氏电路吸引子 3．2 劳伦兹系统(Lorenz System) 1963 年,Lorenz在研究大气对流时,在三维自治系统中发现了第一个混沌吸引子。系统为如下的三阶微分方程组(I)，1993 年，Kevin等提出了一种适于电路实现的Lorenz电路[6]，运用坐标变换： u = x ,10/ v = y ,10/ zw = 20/ ，等到一种新的变形电路，三阶微分方程组如(II)所示：两种吸引子分别如图 3 所示：（I） (II) = = = ( σ rx xy x y ), − y xz −− z − β x ⎧ & ⎪ y ⎨ & ⎪ z ⎩ & u uv ), ( − = & σ ⎧ ⎪ ru v v 20 = −− ⎨ & ⎪ w bw uv 5 − = ⎩ & , 其中 σ = ,10 β = 8 3 , r = 28 ，初始值为 ]1,1,1[ uw , 其中 σ = ,16 b = ,4 r = 6.45 ，初始值为 ]1,1,1[ (a) 劳伦兹系统 I (b) 劳伦兹系统 II 图 3 劳伦兹系统吸引子 4

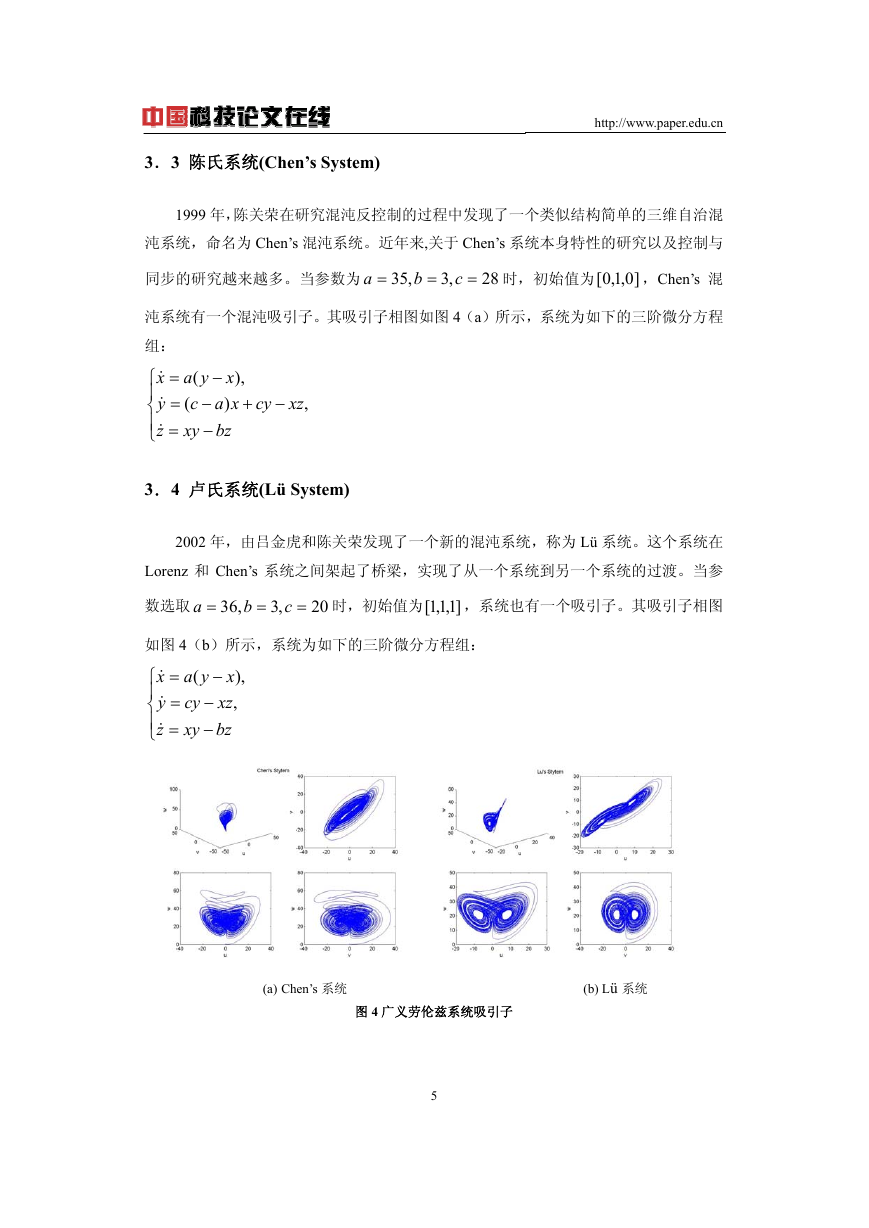
http://www.paper.edu.cn 3．3 陈氏系统(Chen’s System) 1999 年，陈关荣在研究混沌反控制的过程中发现了一个类似结构简单的三维自治混沌系统，命名为 Chen’s 混沌系统。近年来,关于 Chen’s 系统本身特性的研究以及控制与同步的研究越来越多。当参数为 a = ,35 b = ,3 c = 28 时，初始值为 ]0,1,0[ ，Chen’s 混沌系统有一个混沌吸引子。其吸引子相图如图 4（a）所示，系统为如下的三阶微分方程组： x & y & z & ⎧ ⎪ ⎨ ⎪ ⎩ = = = − ya x ( ), xac ) ( + − xy bz − cy − xz , 3．4 卢氏系统(Lü System) 2002 年，由吕金虎和陈关荣发现了一个新的混沌系统，称为 Lü 系统。这个系统在 Lorenz 和 Chen’s 系统之间架起了桥梁，实现了从一个系统到另一个系统的过渡。当参数选取 a = ,36 b = ,3 c = 20 时，初始值为 ]1,1,1[ ，系统也有一个吸引子。其吸引子相图如图 4（b）所示，系统为如下的三阶微分方程组： x & y & z & ⎧ ⎪ ⎨ ⎪ ⎩ = = = x ya ( ), − cy xz , − xy bz − (a) Chen’s 系统 (b) Lü 系统图 4 广义劳伦兹系统吸引子 5

3．5 洛丝勒系统(Rossler System) http://www.paper.edu.cn 1976 年，由 Rossler 在研究具有中间产物的化学反映问题时，通过适当的标度变换，给出了一个很简单的非线性常微分方程组， x & y & z & ⎧ ⎪ ⎨ ⎪ ⎩ y ( −= x += xz ( = 当参数如 ), z + ay , c ) − a 2.0== b + b ， 7.5=c 时，初始值为 ]1,1,1[ ，系统会产生一个奇怪吸引子，如图 5 所示。 4. 总结图 5 洛丝勒系统吸引子在众多三维混沌系统吸引子仿真中发现初始值的选取至关重要。尤其在蔡式电路的初始值的选取时，很细微的差别吸引子的变化是非常明显的，充分证明了混沌现象的初始值的敏感性。而劳伦兹和洛丝勒系统的初始值的选取都选择状态向量。对迭代次数的要求，即步长的选取也是非常重要的，在混沌现象吸引子的产生里面都有一个迭代步长的问题。对蔡式电路实现时，即使初值选的合适，其步长也是直接影响其效果的因素，通常选取区间为：[1,100]，也是为了充分考虑仿真的计算时间与吸引子的效果。在广义的劳伦兹系统里面有一些共同之处：陈氏系统和卢氏系统都是劳伦兹系统的变形，其中卢氏系统是劳伦兹系统和陈氏系统的过渡过程。在实际的系统应用分析中选取何种系统产生混沌从而达到最终的目的，不仅在这些三维混沌的背景上有讲究，同时也要考虑其无量纲后产生的信号的混沌吸引子的特性，即时间序列或者李雅普诺夫指数等相关性质。有待在后续的文章中进一步的分析。参考文献 [1] 郝柏林从抛物线谈起－混沌动力学引论上海科技教育出版社 1995 年； [2] 刘卫国 MATLAB 程序设计教程中国水利水电出版社 2005 年 [3] 盛昭瀚马海军非线性动力系统分析引论科学出版社 2001 年； [4] 苏大生，夏小建利用 Matlab 模拟混沌系统泉州师范学院学报(自然科学) 2003 年 11 月 29-32 [5] Wei Lin and Yangbo He. Complete synchronization of the noise-perturbed Chua's circuits Chaos 15, 023705 (2005) 6

[6] Kevin M.C. and Alan V.O. and Steven H.S. Synchronization of Lorenz-Based Chaotic Circuit with Applications to Communications IEEE Trans on CAS II: Analog and Digital Signal Processing vol. 40,No 10,1993 626-633 http://www.paper.edu.cn Research on the 3-Dimension chaos system attractors based on the MATLAB Zhao Chen1,2 Tianhao Tang1 Dingxin Shen1 1Department of Electric Automation, Shanghai Maritime University, Shanghai (200135) 2Insititue of Information Engineering, China University of Geosciences, Wuhan (430074) Abstract The complex of the research on the chaos is coming from the characteristics of nonlinear. It’s very hard to give the exact value of the nonlinear equation. This paper gives the relation of the several chaos system attractors which based on the simulation of the MATLAB. Key words Chaos Attractor Simulation 7

资料库

论文研究-基于MATLAB的三维混沌系统吸引子的研究 .pdf

相关推荐

开发技术

热门标签

最新资料