任务分配问题.ppt

发布时间：2022-06-03 发布人：admin 分类：说明书资料大小：0.08M 资料格式：ppt 举报版权申诉

qq_40200628-10655152-16359647607634068139.ppt.pdf-第1页.png

第1页 / 共17页

qq_40200628-10655152-16359647607634068139.ppt.pdf-第2页.png

第2页 / 共17页

qq_40200628-10655152-16359647607634068139.ppt.pdf-第3页.png

第3页 / 共17页

qq_40200628-10655152-16359647607634068139.ppt.pdf-第4页.png

第4页 / 共17页

qq_40200628-10655152-16359647607634068139.ppt.pdf-第5页.png

第5页 / 共17页

qq_40200628-10655152-16359647607634068139.ppt.pdf-第6页.png

第6页 / 共17页

qq_40200628-10655152-16359647607634068139.ppt.pdf-第7页.png

第7页 / 共17页

qq_40200628-10655152-16359647607634068139.ppt.pdf-第8页.png

第8页 / 共17页

文本预览

组合问题中的分支限界法任务分配问题主讲人：郭嘉明张旋

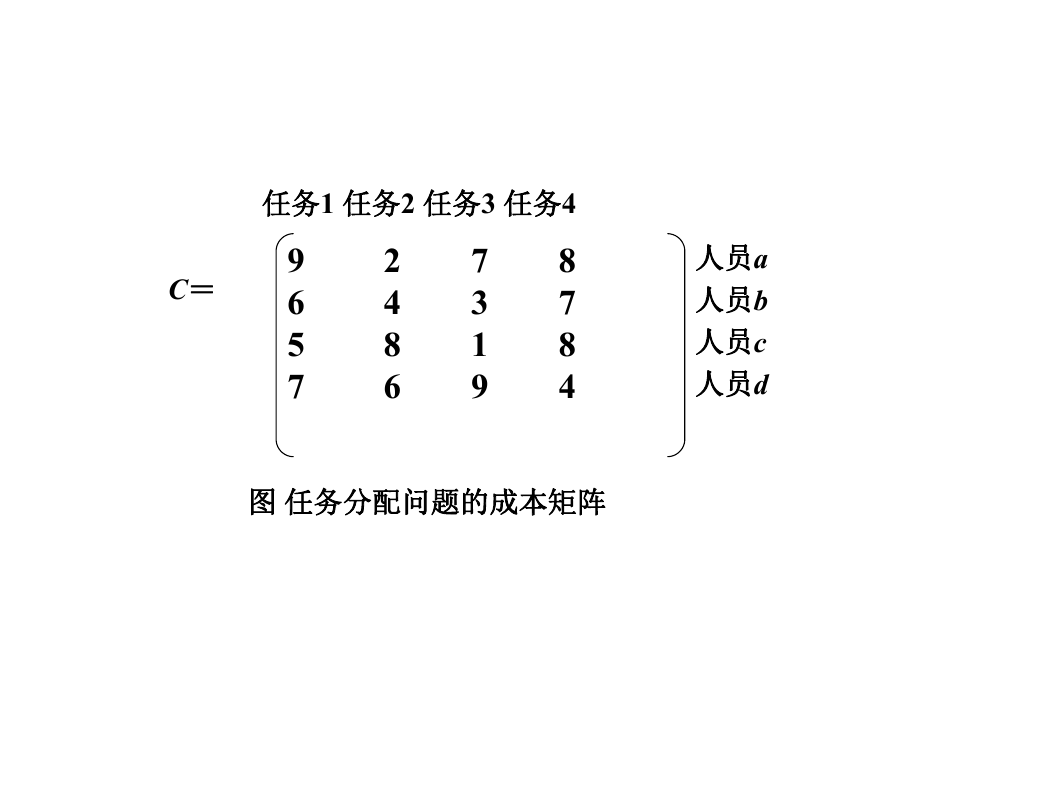
任务分配问题任务分配问题要求把n项任务分配给n个人，每个人完成每项任务的成本不同，要求分配总成本最小的最优分配方案。如图所示是一个任务分配的成本矩阵。 C＝任务1 任务2 任务3 任务4 9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4 人员a 人员b 人员c 人员d 图任务分配问题的成本矩阵

求最优分配成本的上界和下界考虑任意一个可行解，例如矩阵中的对角线是一个合法的选择，表示将任务1分配给人员a、任务2分配给人员b、任务3 分配给人员c、任务4分配给人员d，其成本是9+4+1+4=18；或者应用贪心法求得一个近似解：将任务2分配给人员a、任务3分配给人员b、任务1分配给人员c、任务4分配给人员d，其成本是2+3+5+4=14。显然，14是一个更好的上界。为了获得下界，考虑人员a执行所有任务的最小代价是2，人员b 执行所有任务的最小代价是3，人员c执行所有任务的最小代价是1，人员d执行所有任务的最小代价是4。因此，将每一行的最小元素加起来就得到解的下界，其成本是 2+3+1+4=10。需要强调的是，这个解并不是一个合法的选择（3和1来自于矩阵的同一列），它仅仅给出了一个参考下界，这样，最优值一定是[10, 14]之间的某个值。

设当前已对人员1～i分配了任务，并且获得了成本v，则限界函数可以定义为：行的最小值  v lb n  ik  k 第 1

应用分支限界法求解图所示任务分配问题，对解空间树的搜索如图所示，具体的搜索过程如下：（1）在根结点1，没有分配任务，根据限界函数估算目标函数值为2+3+1+4=10；（2）在结点2，将任务1分配给人员a，获得的成本为9，目标函数值为9 + (3+1+4)=17，超出目标函数的界[10, 14]，将结点2 丢弃；在结点3，将任务2分配给人员a，获得的成本为2，目标函数值为2 + (3+1+4)=10，将结点3加入待处理结点表PT中；在结点4，将任务3分配给人员a，获得的成本为7，目标函数值为 7 + (3+1+4)=15，超出目标函数的界[10, 14]，将结点4丢弃；在结点5，将任务4分配给人员a，获得的成本为8，目标函数值为 8 + (3+1+4)=16，超出目标函数的界[10, 14]，将结点5丢弃；

（3）在表PT中选取目标函数值极小的结点3优先进行搜索；（4）在结点6，将任务1分配给人员b，获得的成本为2+6=8，目标函数值为8+(1+4)＝13，将结点6加入表PT中；在结点7，将任务3分配给人员b，获得的成本为2+3=5，目标函数值为 5+(1+4)＝10，将结点7加入表PT中；在结点8。将任务4分配给人员b，获得的成本为2+7=9，目标函数值为9+(1+4)＝14，将结点8加入表PT中；（5）在表PT中选取目标函数值极小的结点7优先进行搜索；（6）在结点9，将任务1分配给人员c，获得的成本为5+5=10，目标函数值为10+4=14，将结点9加入表PT中；在结点10，将任务4分配给人员c，获得的成本为5+8=13，目标函数值为 13+4=17，超出目标函数的界[10, 14]，将结点10丢弃；

（7）在表PT中选取目标函数值极小的结点6优先进行搜索；（8）在结点11，将任务3分配给人员c，获得的成本为8+1=9，目标函数值为9+4=13，将结点11加入表PT中；在结点12，将任务4分配给人员c，获得的成本为8+8=16，目标函数值为 16+4=20，超出目标函数的界[10, 14]，将结点12丢弃；（9）在表PT中选取目标函数值极小的结点11优先进行搜索；（10）在结点13，将任务4分配给人员d，获得的成本为 9+4=13，目标函数值为13，由于结点13是叶子结点，同时结点13的目标函数值是表PT中的极小值，所以，结点13对应的解即是问题的最优解，搜索结束。

C＝任务1 任务2 任务3 任务4 9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4 人员a 人员b 人员c 人员d 图任务分配问题的成本矩阵

分享到：

赞收藏

资料库

任务分配问题.ppt

相关推荐

大数据

热门标签

最新资料