2022年江苏常州中考数学试题及答案.doc

发布时间：2022-08-24 发布人：admin 分类：说明书资料大小：3.32M 资料格式：doc 举报版权申诉

第1页 / 共21页

第2页 / 共21页

第3页 / 共21页

第4页 / 共21页

第5页 / 共21页

第6页 / 共21页

第7页 / 共21页

第8页 / 共21页

文本预览

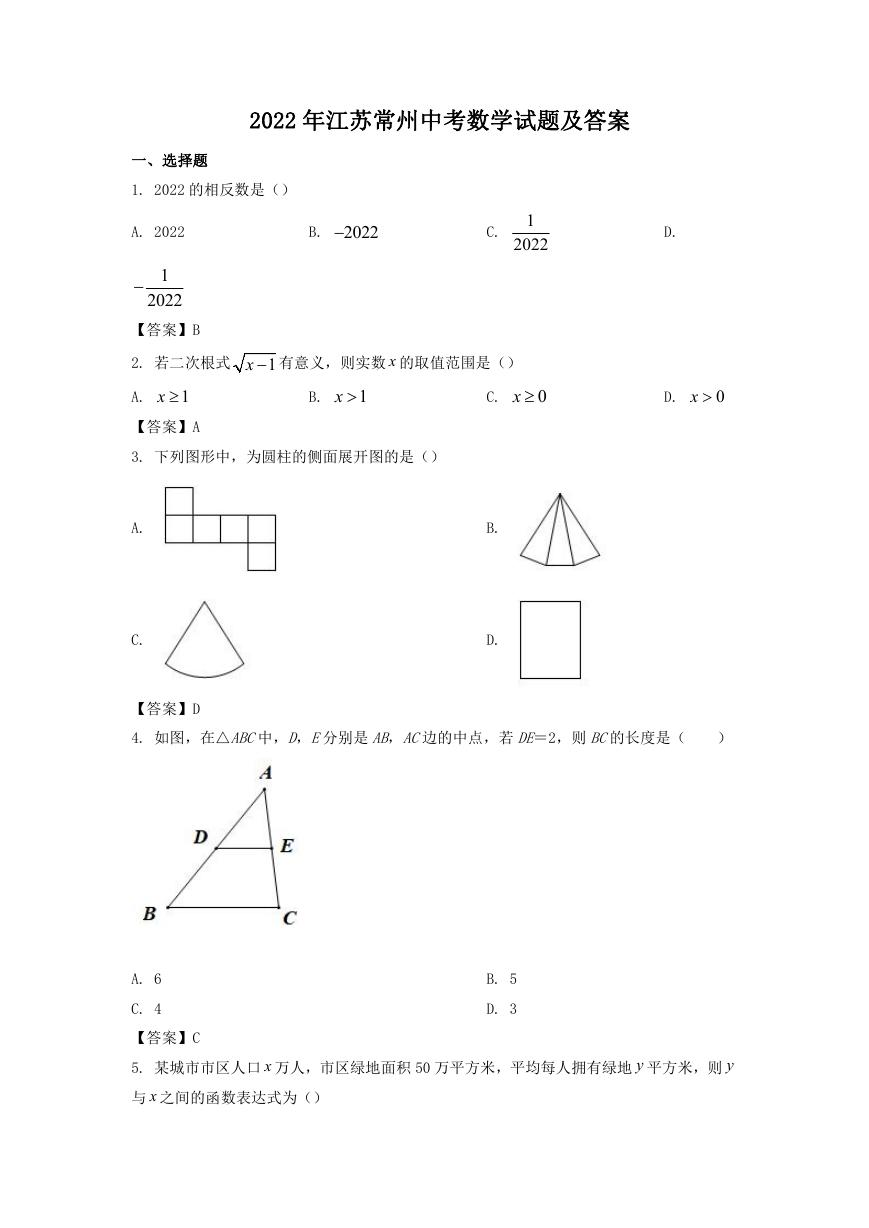
2022 年江苏常州中考数学试题及答案一、选择题 1. 2022 的相反数是（） A. 2022  1 2022 【答案】B B. 2022  C. 1 2022 D. 2. 若二次根式 1x  有意义，则实数 x 的取值范围是（） A. 1x 【答案】A B. 1x  C. 0x  D. x  0 3. 下列图形中，为圆柱的侧面展开图的是（） A. C. 【答案】D B. D. 4. 如图，在△ABC中，D，E分别是 AB，AC边的中点，若 DE＝2，则 BC的长度是（） A. 6 C. 4 B. 5 D. 3 【答案】C 5. 某城市市区人口 x 万人，市区绿地面积 50 万平方米，平均每人拥有绿地 y 平方米，则 y 与 x 之间的函数表达式为（）

A. y x  50 B. y  50 x C. y  50 x D. y  x 50 【答案】C 6. 如图，斑马线的作用是为了引导行人安全地通过马路．小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一想法体现的数学依据是（） A. 垂线段最短 B. 两点确定一条直线 C. 过一点有且只有一条直线与已知直线垂直 D. 过直线外一点有且只有一条直线与已知直线平行【答案】A 7. 在平面直角坐标系 xOy 中，点 A与点 1A 关于 x 轴对称，点 A与点 2A 关于 y 轴对称．已知点 1(1,2) A. ( 2,1) ( 1, 2)   ，则点 2A 的坐标是（） C. ( 1,2) B. ( 2, 1)   D. A   【答案】D 8. 某汽车评测机构对市面上多款新能源汽车的 0 ~100 进行了性能评测，评测结果绘制如下，每个点都对应一款新能源汽车的评测数据．已知 km 的加速时间的中位数是 sm ，满电续航里程的中位数是 nkm ，相应的直线将 0 ~100 平面分成了①、②、③、④四个区域（直线不属于任何区域）．欲将最新上市的两款新能源 km 的加速时间和满电续航里程 / h / h 汽车的评测数据对应的点绘制到平面内，若以上两组数据的中位数均保持不变，则这两个点可能分别落在（）

A. 区域①、② B. 区域①、③ C. 区域①、④ D. 区域 ③、④ 【答案】B 二、填空题 9. 计算： 3 8 =___．【答案】2 【详解】解：∵23=8， ∴ 3 8=2 ，故答案为：2． 10. 计算： 4 m m _______． 2  【答案】 2m 【详解】解： 4 m m m  ．  2 2 故答案为： 2m ． 11. 分解因式： 2 x y 【答案】xy(x+y) 2 xy  ______． 2 【详解】 2 x y y xy x  故答案为： ( xy x y ．  ) ( x  y ) ， 12. 2022 年 5 月 22 日，中国科学院生物多样性委员会发布《中国生物物种名录》2022 版，共收录物种及种下单元约 138000 个．数据 138000 用科学记数法表示为______．【答案】1.38×105 【详解】解：由题意可知： 138000=1.38×105，故答案为：1.38×105

13. 如图，数轴上的点 A 、B 分别表示实数 a 、b ，则 1 a ______ 1 b ．（填“>”、“=”或“<”）【答案】  【详解】解：由图可得：1 a b   ，由不等式的性质得：故答案为： ． 14. 如图，在 ABC 是______． 1 a  ， 1 b 中， E 是中线 AD 的中点．若 AEC△ 的面积是 1，则 ABD△ 的面积   的面积 1 ，的面积 DCE    的面积 ACD 【答案】2 【详解】解： AD 是 BC 边上的中线， E 为 AD 的中点，根据等底同高可知， ACE ABD 故答案为：2． 15. 如图，将一个边长为 20cm 的正方形活动框架（边框粗细忽略不计）扭动成四边形 ABCD ，对角线是两根橡皮筋，其拉伸长度达到36cm 时才会断裂．若皮筋 AC _____断裂（填“会”或“不会”，参考数据： 3 1.732 的面积 2 ，的面积 2 AEC   BAD  60  ，则橡  ）．【答案】不会【详解】解：设扭动后对角线的交点为O ，如下图：

 BAD  根据正方形的性质得， 60  ， 20  ，得出扭动后的四边形四边相等为菱形， AD AB ABD BD  ，为等边三角形， 20 1 2  ， BD 10   BO  AO  2 AB  2 BO  10 3 ，根据菱形的对角线的性质： AC AO 2  20 3  34.64 ， 34.64 36  AC 不会断裂，，故答案为：不会． 16. 如图， ABC ______．是 O 的内接三角形．若 ABC  45  ， AC  ，则 O 的半径是 2 【答案】1 【详解】解：连接OA 、OC ，

   ， 45 ABC   2 ABC AOC   OA OC   OA  ， 2 2 解得： 1 故答案为：1． 17. 如图，在四边形 ABCD 中， CD  ，则sin ABD 3  ______．  90  ， AC 2 ，即 2 OA  ， 2 2    A ABC  90  ， DB 平分 ADC ．若 AD  ， 1 【答案】 6 6 【详解】解：过点 D 作 BC 的垂线交于 E ， 90 DEB    ABC A     ， 四边形 ABED 为矩形， 1  DE AB AD BE 90     ， / / ABD ,    BDQ    BDE ，平分 ADC ，，   ADB / / AD BE ADB CDB ， CBD   ，   ∴∠CDB=∠CBD 3 ， CD CB AD BE   ， 1 

∴ CE  2 ，  DE  2 DC  CE 2  9 4   ， 5   BD 2 DE  BE 2  5 1   6   sin BDE  BE BD  1 6  6 6 ，   sin ABD  6 6 ，故答案为： 6 6 ． 4 3 中， 90  ， C  AC  ， 9 EF  ．用一条始终绷直的弹性染色线连接CF ，Rt DEF 18. 如图，在 Rt ABC△ DF  ，与点 B 重合）平移至终止位置（点 E 与点 A 重合），且斜边 DE 始终在线段 AB 上，则 Rt ABC△ 的外部．．被染色的区域面积是______． BC  ．在 Rt DEF 12   中， F  90  ，从起始位置（点 D 【答案】28 【详解】解：过点 F 作 AB 的垂线交于G ，同时在图上标出 , ,M N F 如下图：  C  90  ， AC  ， 9 BC  ， 12   AB 2 AC  2 BC 15  ，

在 Rt DEF  中， F  90  ， DF  ， 3 EF  ． 4 2 2   / / 15 5 10 DF   , 5  ，    FE DE  AE AB DE  EF AF EF AF     四边形 AEFF 为平行四边形，   10  ，，， AE FF 1 2 DEF  S  DF EF   1 2 DE GF   6 ，解得： GF  ， 12 5 ACM FDM  ,   CAM ， DF   ，   / / AC DFM DFM ACM ∽ 1 DM DF 3 AM AC    ，  ，  DM  1 3 AM  1 4 AB  ， 15 4  ， / / BC AF  AN AF BC DN  同理可证： ANF 1 3 3 4 DN AN   3     ，  ∽ DNC ， AB  ， 45 4  MN DN DM    45 15 4 4   ， 30 4 Rt ABC 的外部被染色的区域面积为 S 梯形  MNF F   1 2    30 4  10     12 5  28 ，故答案为：28．三、解答题 19. 计算：（1） ( 2) 2  (   0 3)  1 3 ；（2） ( x 2  1)  ( x  1)( x  1) ．【答案】（1） 4 3

分享到：

赞收藏

资料库

2022年江苏常州中考数学试题及答案.doc

相关推荐

中考

热门标签

最新资料