第1页 / 共14页
第2页 / 共14页
第3页 / 共14页
第4页 / 共14页
第5页 / 共14页
第6页 / 共14页
第7页 / 共14页
第8页 / 共14页
信号处理_python科学计算.pdf
14-6-19
频域信号处理 — 用Python做科学计算
18 频域信号处理
用FFT(快速傅立叶变换)能将时域的数字信号转换为频域信号。转换为频域信号之后我们可
以很方便地分析出信号的频率成分，在频域上进行处理，最终还可以将处理完毕的频域信
号通过IFFT(逆变换)转换为时域信号，实现许多在时域无法完成的信号处理算法。本章通
过几个实例，简单地介绍有关频域信号处理的一些基本知识。
18.1 观察信号的频谱
将时域信号通过FFT转换为频域信号之后，将其各个频率分量的幅值绘制成图，可以很直观
地观察信号的频谱。下面的程序完成这一任务：
# -*- coding: utf-8 -*-
import numpy as np
import pylab as pl
sampling_rate = 8000
fft_size = 512
t = np.arange(0, 1.0, 1.0/sampling_rate)
x = np.sin(2*np.pi*156.25*t) + 2*np.sin(2*np.pi*234.375*t)
xs = x[:fft_size]
xf = np.fft.rfft(xs)/fft_size
freqs = np.linspace(0, sampling_rate/2, fft_size/2+1)
xfp = 20*np.log10(np.clip(np.abs(xf), 1e-20, 1e100))
pl.figure(figsize=(8,4))
pl.subplot(211)
pl.plot(t[:fft_size], xs)
pl.xlabel(u"时间(秒)")
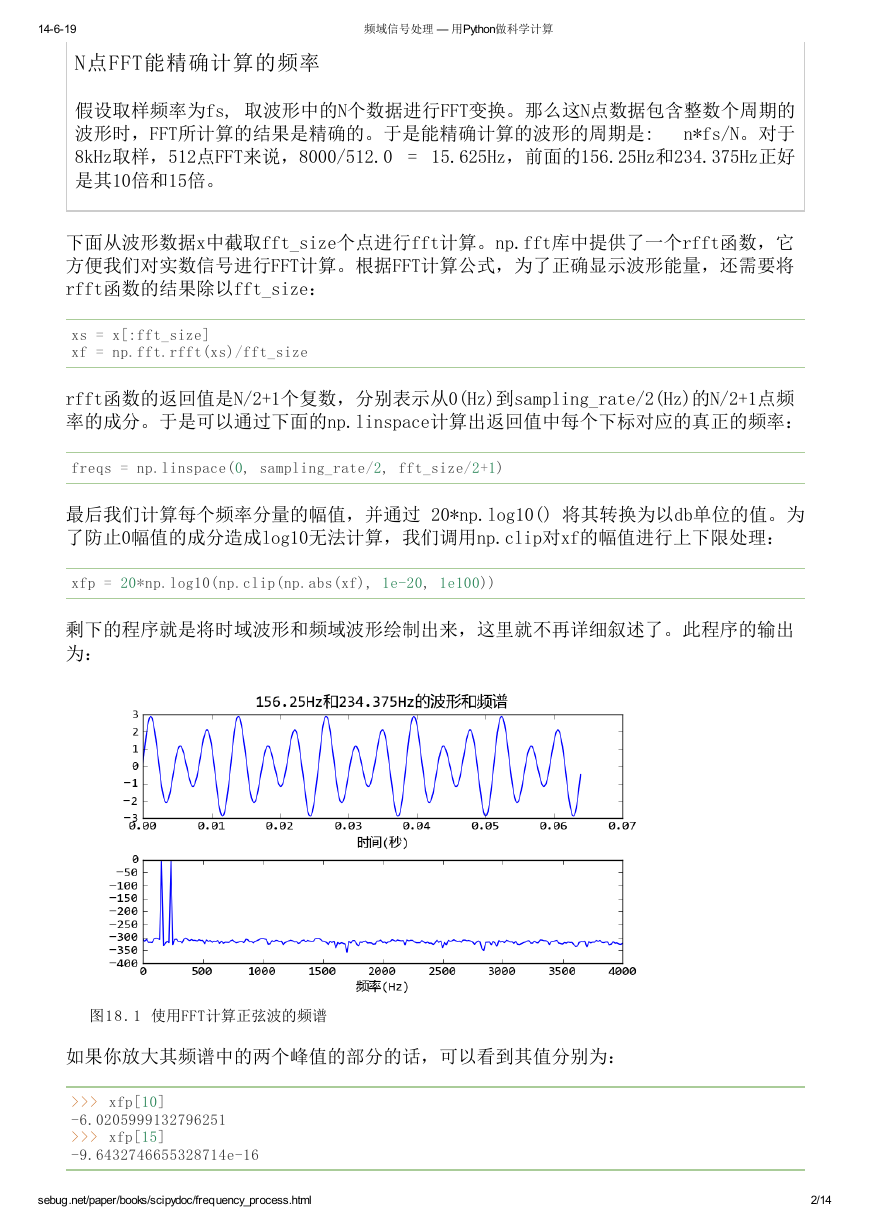
pl.title(u"156.25Hz和234.375Hz的波形和频谱")
pl.subplot(212)
pl.plot(freqs, xfp)
pl.xlabel(u"频率(Hz)")
pl.subplots_adjust(hspace=0.4)
pl.show()
下面逐行对这个程序进行解释：
首先定义了两个常数：sampling_rate, fft_size，分别表示数字信号的取样频率和FFT的
长度。
然后调用np.arange产生1秒钟的取样时间，t中的每个数值直接表示取样点的时间，因此其
间隔为取样周期1/sampline_rate：
t = np.arange(0, 1.0, 1.0/sampling_rate)
用取样时间数组t可以很方便地调用函数计算出波形数据，这里计算的是两个正弦波的叠
加，一个频率是156.25Hz，一个是234.375Hz：
x = np.sin(2*np.pi*156.25*t) + 2*np.sin(2*np.pi*234.375*t)
为什么选择这两个奇怪的频率呢？因为这两个频率的正弦波在512个取样点中正好有整数个
周期。满足这个条件波形的FFT结果能够精确地反映其频谱。
sebug.net/paper/books/scipydoc/frequency_process.html
1/14
14-6-19
频域信号处理 — 用Python做科学计算
N点FFT能精确计算的频率
假设取样频率为fs, 取波形中的N个数据进行FFT变换。那么这N点数据包含整数个周期的
波形时，FFT所计算的结果是精确的。于是能精确计算的波形的周期是:
n*fs/N。对于
8kHz取样，512点FFT来说，8000/512.0 = 15.625Hz，前面的156.25Hz和234.375Hz正好
是其10倍和15倍。
下面从波形数据x中截取fft_size个点进行fft计算。np.fft库中提供了一个rfft函数，它
方便我们对实数信号进行FFT计算。根据FFT计算公式，为了正确显示波形能量，还需要将
rfft函数的结果除以fft_size：
xs = x[:fft_size]
xf = np.fft.rfft(xs)/fft_size
rfft函数的返回值是N/2+1个复数，分别表示从0(Hz)到sampling_rate/2(Hz)的N/2+1点频
率的成分。于是可以通过下面的np.linspace计算出返回值中每个下标对应的真正的频率：
freqs = np.linspace(0, sampling_rate/2, fft_size/2+1)
最后我们计算每个频率分量的幅值，并通过 20*np.log10() 将其转换为以db单位的值。为
了防止0幅值的成分造成log10无法计算，我们调用np.clip对xf的幅值进行上下限处理：
xfp = 20*np.log10(np.clip(np.abs(xf), 1e-20, 1e100))
剩下的程序就是将时域波形和频域波形绘制出来，这里就不再详细叙述了。此程序的输出
为：
图1 8 . 1 使用FFT计算正弦波的频谱
如果你放大其频谱中的两个峰值的部分的话，可以看到其值分别为：
>>> xfp[10]
-6.0205999132796251
>>> xfp[15]
-9.6432746655328714e-16
sebug.net/paper/books/scipydoc/frequency_process.html
2/14
14-6-19
频域信号处理 — 用Python做科学计算
即156.25Hz的成分为-6dB， 而234.375Hz的成分为0dB，与波形的计算公式中的各个分量的
能量(振幅值/2)符合。
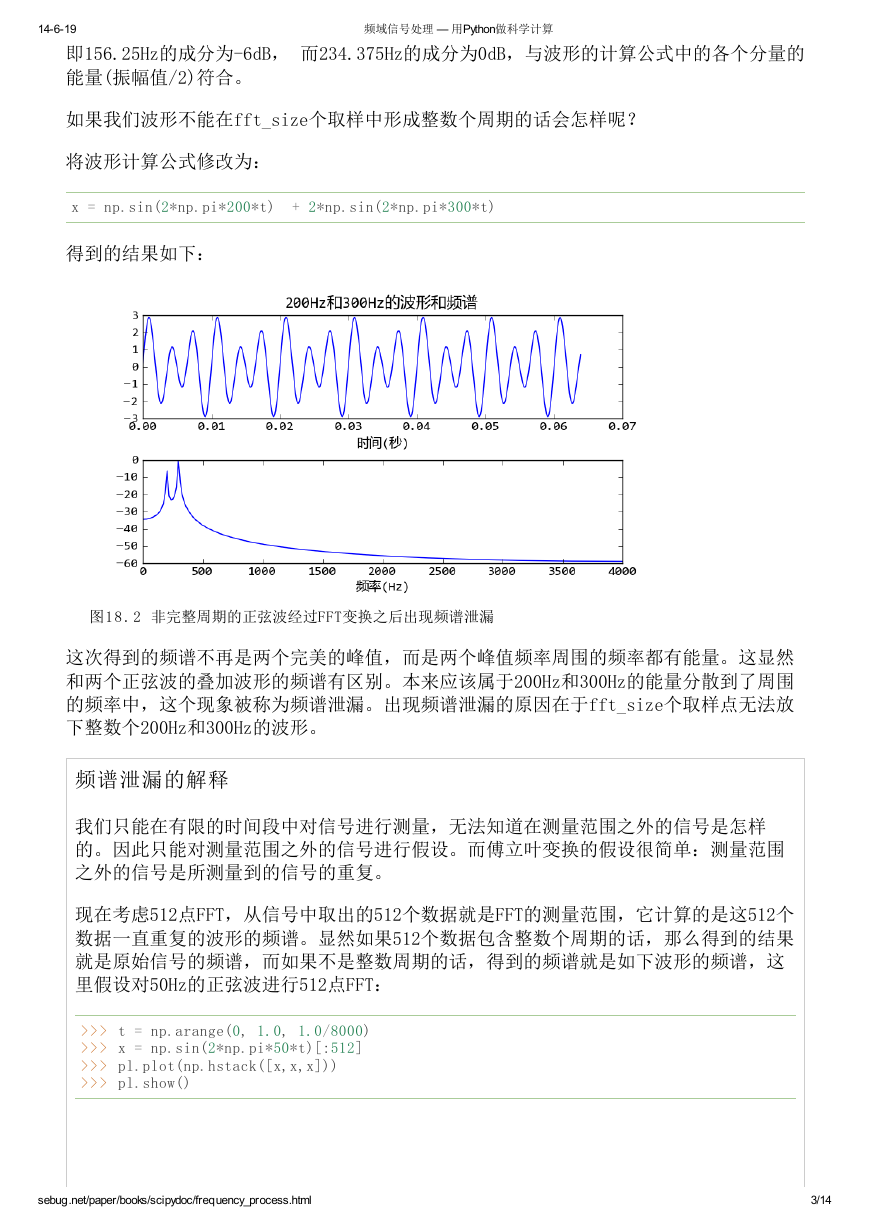
如果我们波形不能在fft_size个取样中形成整数个周期的话会怎样呢？
将波形计算公式修改为：
x = np.sin(2*np.pi*200*t) + 2*np.sin(2*np.pi*300*t)
得到的结果如下：
图1 8 . 2 非完整周期的正弦波经过FFT变换之后出现频谱泄漏
这次得到的频谱不再是两个完美的峰值，而是两个峰值频率周围的频率都有能量。这显然
和两个正弦波的叠加波形的频谱有区别。本来应该属于200Hz和300Hz的能量分散到了周围
的频率中，这个现象被称为频谱泄漏。出现频谱泄漏的原因在于fft_size个取样点无法放
下整数个200Hz和300Hz的波形。
频谱泄漏的解释
我们只能在有限的时间段中对信号进行测量，无法知道在测量范围之外的信号是怎样
的。因此只能对测量范围之外的信号进行假设。而傅立叶变换的假设很简单：测量范围
之外的信号是所测量到的信号的重复。
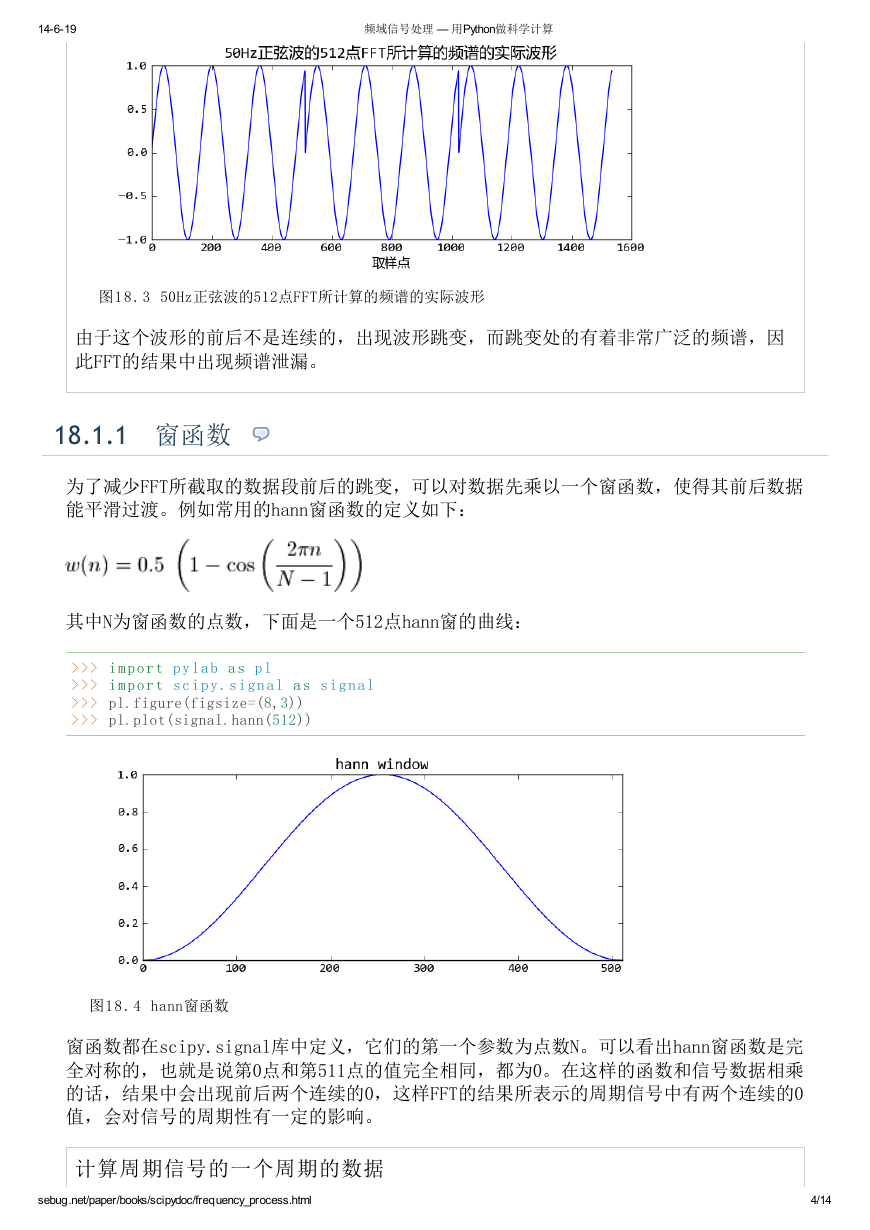
现在考虑512点FFT，从信号中取出的512个数据就是FFT的测量范围，它计算的是这512个
数据一直重复的波形的频谱。显然如果512个数据包含整数个周期的话，那么得到的结果
就是原始信号的频谱，而如果不是整数周期的话，得到的频谱就是如下波形的频谱，这
里假设对50Hz的正弦波进行512点FFT：
>>> t = np.arange(0, 1.0, 1.0/8000)
>>> x = np.sin(2*np.pi*50*t)[:512]
>>> pl.plot(np.hstack([x,x,x]))
>>> pl.show()
sebug.net/paper/books/scipydoc/frequency_process.html
3/14
14-6-19
频域信号处理 — 用Python做科学计算
图1 8 . 3 50Hz正弦波的512点FFT所计算的频谱的实际波形
由于这个波形的前后不是连续的，出现波形跳变，而跳变处的有着非常广泛的频谱，因
此FFT的结果中出现频谱泄漏。
18.1.1 窗函数
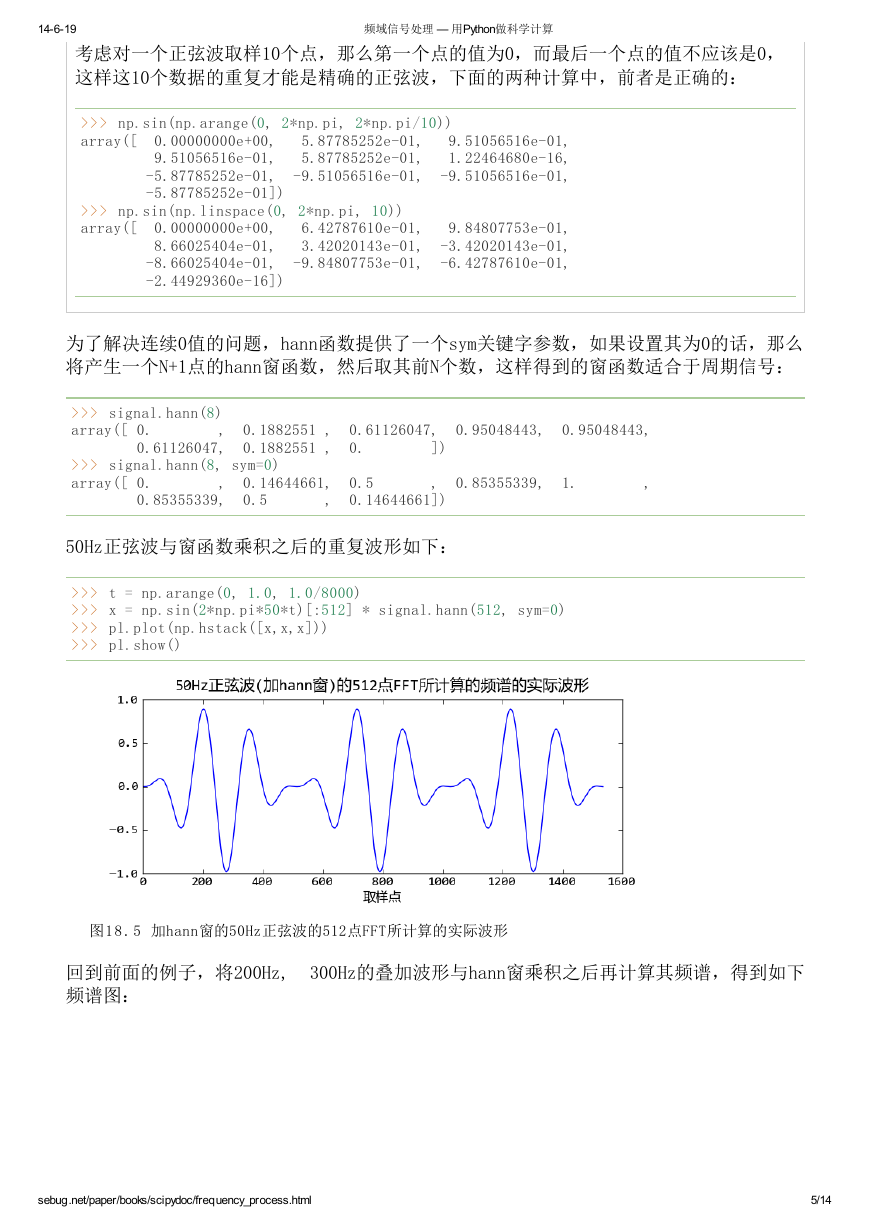
为了减少FFT所截取的数据段前后的跳变，可以对数据先乘以一个窗函数，使得其前后数据
能平滑过渡。例如常用的hann窗函数的定义如下：
其中N为窗函数的点数，下面是一个512点hann窗的曲线：
>>> import pylab as pl
>>> import scipy.signal as signal
>>> pl.figure(figsize=(8,3))
>>> pl.plot(signal.hann(512))
图1 8 . 4 hann窗函数
窗函数都在scipy.signal库中定义，它们的第一个参数为点数N。可以看出hann窗函数是完
全对称的，也就是说第0点和第511点的值完全相同，都为0。在这样的函数和信号数据相乘
的话，结果中会出现前后两个连续的0，这样FFT的结果所表示的周期信号中有两个连续的0
值，会对信号的周期性有一定的影响。
计算周期信号的一个周期的数据
sebug.net/paper/books/scipydoc/frequency_process.html
4/14
14-6-19
频域信号处理 — 用Python做科学计算
考虑对一个正弦波取样10个点，那么第一个点的值为0，而最后一个点的值不应该是0，
这样这10个数据的重复才能是精确的正弦波，下面的两种计算中，前者是正确的：
>>> np.sin(np.arange(0, 2*np.pi, 2*np.pi/10))
array([ 0.00000000e+00, 5.87785252e-01, 9.51056516e-01,
9.51056516e-01, 5.87785252e-01, 1.22464680e-16,
-5.87785252e-01, -9.51056516e-01, -9.51056516e-01,
-5.87785252e-01])
>>> np.sin(np.linspace(0, 2*np.pi, 10))
array([ 0.00000000e+00, 6.42787610e-01, 9.84807753e-01,
8.66025404e-01, 3.42020143e-01, -3.42020143e-01,
-8.66025404e-01, -9.84807753e-01, -6.42787610e-01,
-2.44929360e-16])
为了解决连续0值的问题，hann函数提供了一个sym关键字参数，如果设置其为0的话，那么
将产生一个N+1点的hann窗函数，然后取其前N个数，这样得到的窗函数适合于周期信号：
>>> signal.hann(8)
array([ 0. , 0.1882551 , 0.61126047, 0.95048443, 0.95048443,
0.61126047, 0.1882551 , 0. ])
>>> signal.hann(8, sym=0)
array([ 0. , 0.14644661, 0.5 , 0.85355339, 1. ,
0.85355339, 0.5 , 0.14644661])
50Hz正弦波与窗函数乘积之后的重复波形如下：
>>> t = np.arange(0, 1.0, 1.0/8000)
>>> x = np.sin(2*np.pi*50*t)[:512] * signal.hann(512, sym=0)
>>> pl.plot(np.hstack([x,x,x]))
>>> pl.show()
图1 8 . 5 加hann窗的50Hz正弦波的512点FFT所计算的实际波形
回到前面的例子，将200Hz, 300Hz的叠加波形与hann窗乘积之后再计算其频谱，得到如下
频谱图：
sebug.net/paper/books/scipydoc/frequency_process.html
5/14
14-6-19
频域信号处理 — 用Python做科学计算
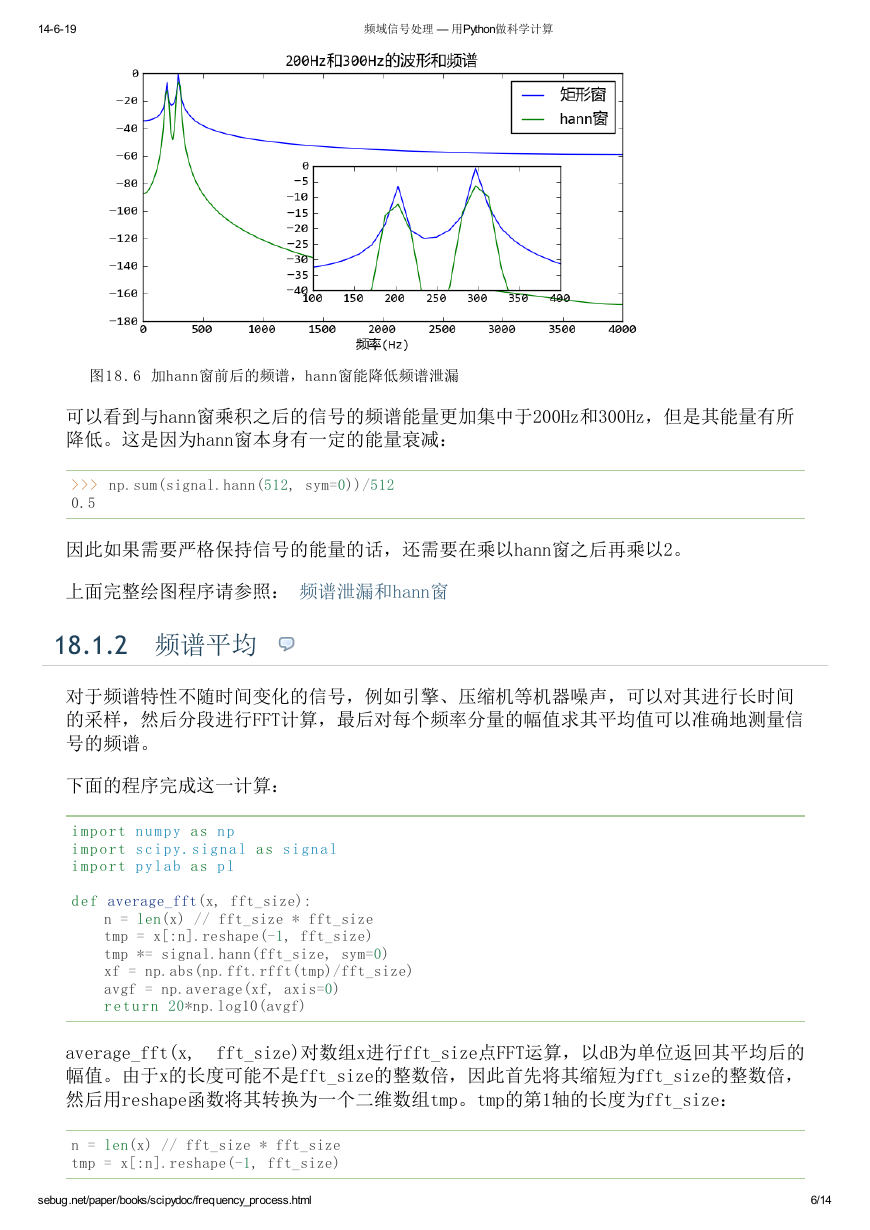
图1 8 . 6 加hann窗前后的频谱，hann窗能降低频谱泄漏
可以看到与hann窗乘积之后的信号的频谱能量更加集中于200Hz和300Hz，但是其能量有所
降低。这是因为hann窗本身有一定的能量衰减：
>>> np.sum(signal.hann(512, sym=0))/512
0.5
因此如果需要严格保持信号的能量的话，还需要在乘以hann窗之后再乘以2。
上面完整绘图程序请参照： 频谱泄漏和hann窗
18.1.2 频谱平均
对于频谱特性不随时间变化的信号，例如引擎、压缩机等机器噪声，可以对其进行长时间
的采样，然后分段进行FFT计算，最后对每个频率分量的幅值求其平均值可以准确地测量信
号的频谱。
下面的程序完成这一计算：
import numpy as np
import scipy.signal as signal
import pylab as pl
def average_fft(x, fft_size):
n = len(x) // fft_size * fft_size
tmp = x[:n].reshape(-1, fft_size)
tmp *= signal.hann(fft_size, sym=0)
xf = np.abs(np.fft.rfft(tmp)/fft_size)
avgf = np.average(xf, axis=0)
return 20*np.log10(avgf)
average_fft(x, fft_size)对数组x进行fft_size点FFT运算，以dB为单位返回其平均后的
幅值。由于x的长度可能不是fft_size的整数倍，因此首先将其缩短为fft_size的整数倍，
然后用reshape函数将其转换为一个二维数组tmp。tmp的第1轴的长度为fft_size：
n = len(x) // fft_size * fft_size
tmp = x[:n].reshape(-1, fft_size)
sebug.net/paper/books/scipydoc/frequency_process.html
6/14
14-6-19
频域信号处理 — 用Python做科学计算
然后将tmp的第1轴上的数据和窗函数相乘，这里选用的是hann窗：
tmp *= signal.hann(fft_size, sym=0)
调用rfft对tmp每的行数据进行FFT计算，并求其幅值：
xf = np.abs(np.fft.rfft(tmp)/fft_size)
接下来调用average函数对xf沿着第0轴进行平均，这样就得到每个频率分量的平均幅值：
avgf = np.average(xf, axis=0)
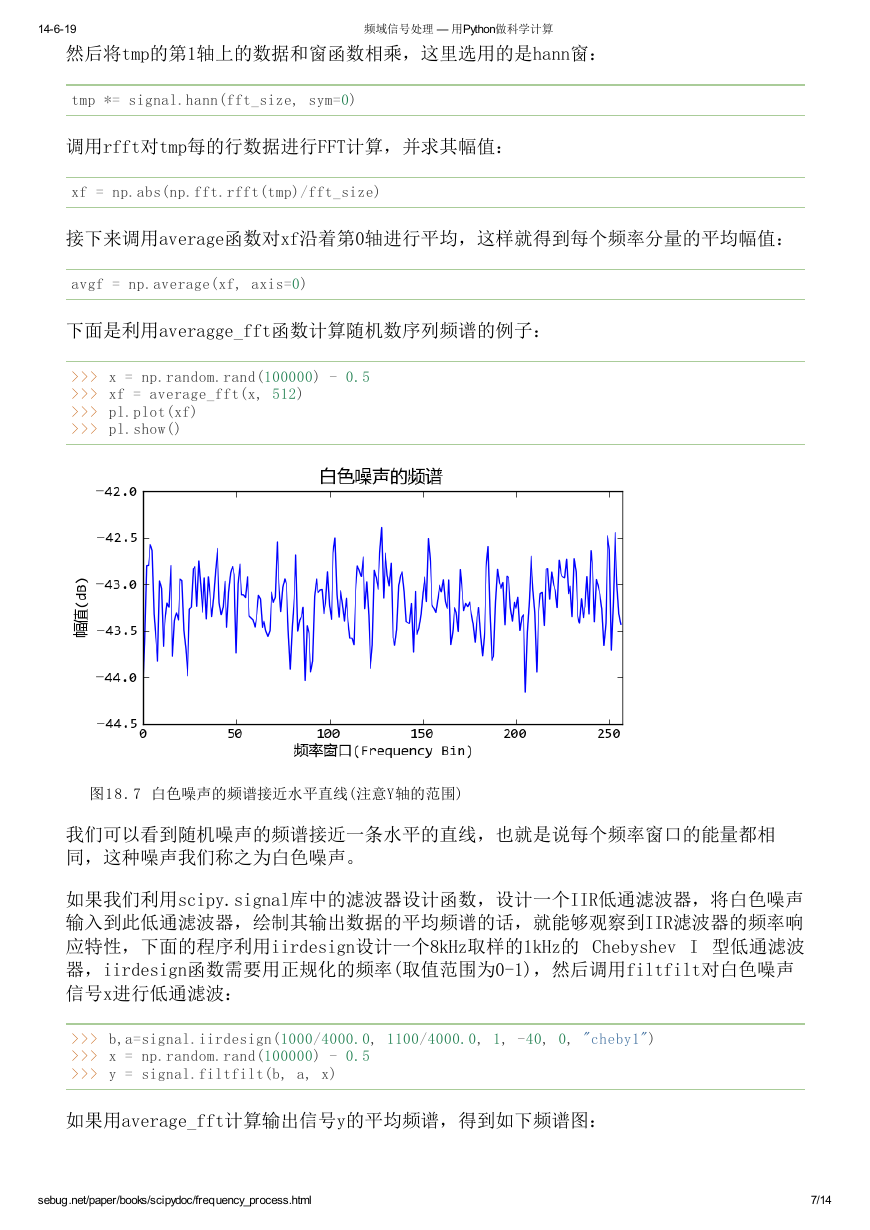
下面是利用averagge_fft函数计算随机数序列频谱的例子：
>>> x = np.random.rand(100000) - 0.5
>>> xf = average_fft(x, 512)
>>> pl.plot(xf)
>>> pl.show()
图1 8 . 7 白色噪声的频谱接近水平直线(注意Y轴的范围)
我们可以看到随机噪声的频谱接近一条水平的直线，也就是说每个频率窗口的能量都相
同，这种噪声我们称之为白色噪声。
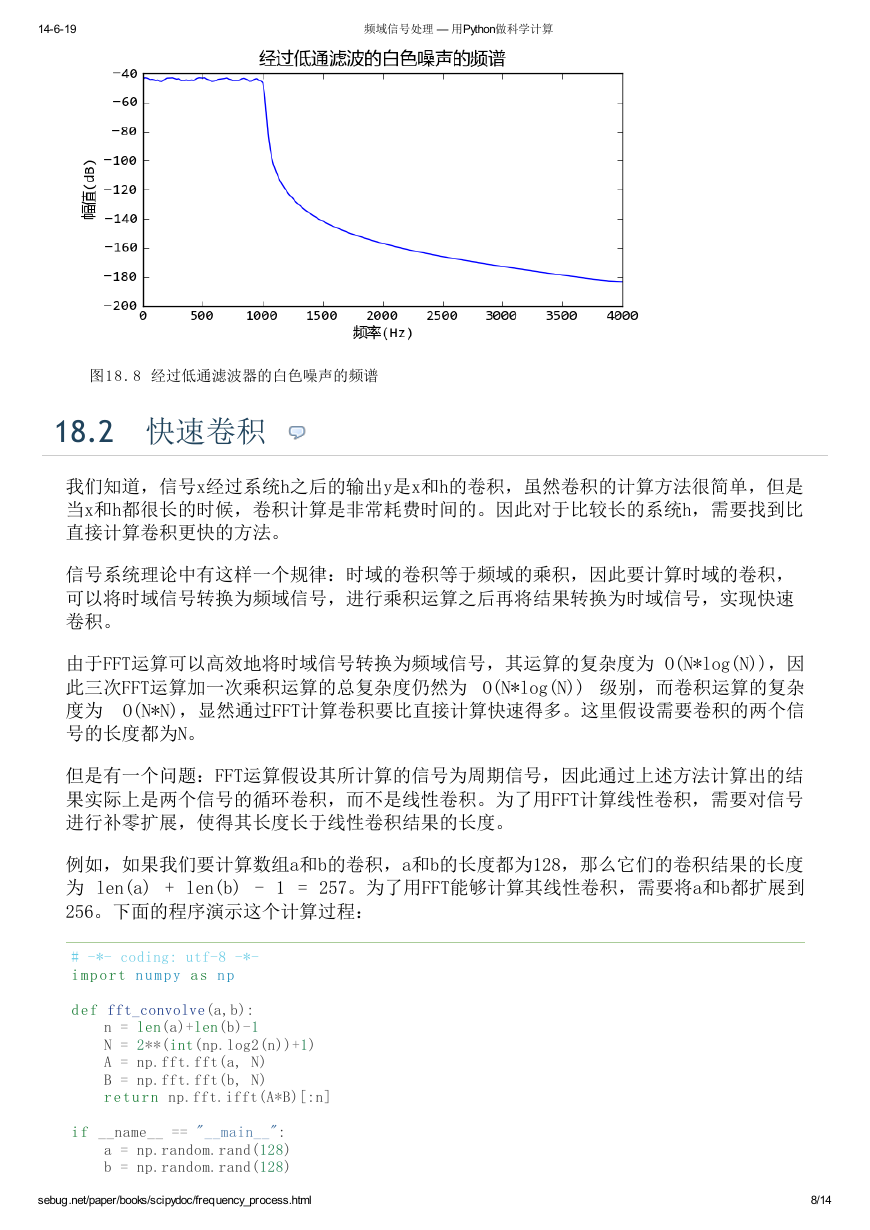
如果我们利用scipy.signal库中的滤波器设计函数，设计一个IIR低通滤波器，将白色噪声
输入到此低通滤波器，绘制其输出数据的平均频谱的话，就能够观察到IIR滤波器的频率响
应特性，下面的程序利用iirdesign设计一个8kHz取样的1kHz的 Chebyshev I 型低通滤波
器，iirdesign函数需要用正规化的频率(取值范围为0-1)，然后调用filtfilt对白色噪声
信号x进行低通滤波：
>>> b,a=signal.iirdesign(1000/4000.0, 1100/4000.0, 1, -40, 0, "cheby1")
>>> x = np.random.rand(100000) - 0.5
>>> y = signal.filtfilt(b, a, x)
如果用average_fft计算输出信号y的平均频谱，得到如下频谱图：
sebug.net/paper/books/scipydoc/frequency_process.html
7/14
14-6-19
频域信号处理 — 用Python做科学计算
图1 8 . 8 经过低通滤波器的白色噪声的频谱
18.2 快速卷积
我们知道，信号x经过系统h之后的输出y是x和h的卷积，虽然卷积的计算方法很简单，但是
当x和h都很长的时候，卷积计算是非常耗费时间的。因此对于比较长的系统h，需要找到比
直接计算卷积更快的方法。
信号系统理论中有这样一个规律：时域的卷积等于频域的乘积，因此要计算时域的卷积，
可以将时域信号转换为频域信号，进行乘积运算之后再将结果转换为时域信号，实现快速
卷积。
由于FFT运算可以高效地将时域信号转换为频域信号，其运算的复杂度为 O(N*log(N))，因
此三次FFT运算加一次乘积运算的总复杂度仍然为 O(N*log(N)) 级别，而卷积运算的复杂
度为 O(N*N)，显然通过FFT计算卷积要比直接计算快速得多。这里假设需要卷积的两个信
号的长度都为N。
但是有一个问题：FFT运算假设其所计算的信号为周期信号，因此通过上述方法计算出的结
果实际上是两个信号的循环卷积，而不是线性卷积。为了用FFT计算线性卷积，需要对信号
进行补零扩展，使得其长度长于线性卷积结果的长度。
例如，如果我们要计算数组a和b的卷积，a和b的长度都为128，那么它们的卷积结果的长度
为 len(a) + len(b) - 1 = 257。为了用FFT能够计算其线性卷积，需要将a和b都扩展到
256。下面的程序演示这个计算过程：
# -*- coding: utf-8 -*-
import numpy as np
def fft_convolve(a,b):
n = len(a)+len(b)-1
N = 2**(int(np.log2(n))+1)
A = np.fft.fft(a, N)
B = np.fft.fft(b, N)
return np.fft.ifft(A*B)[:n]
if __name__ == "__main__":
a = np.random.rand(128)
b = np.random.rand(128)
sebug.net/paper/books/scipydoc/frequency_process.html
8/14
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
