logo资料库

GARCH模型中美式亚式期权价值的蒙特卡罗模拟算法.pdf

发布时间：2022-06-10 发布人：admin 分类：说明书 资料大小：0.47M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    2 2 Ξ 第 21 卷第 2 期 2004 年 6 月 　　　　　　 　　 　　　　　　　 　V o l. 21　N o. 2 Jun. 2004 经　济　数　学 M A TH EM A T ICS IN ECONOM ICS GARCH 模型中美式亚式 期权价值的蒙特卡罗模拟算法 邵　斌　丁　娟 (上海财经大学, 证券期货学院, 上海　200433) 摘　要　我们运用 L ongstaff 和 Schw artz 最近提出的用蒙特卡罗模拟法计算美式期权的方法在 GA RCH 模 型中求解美式亚式期权, 我们的结果表明和其它数值方法相比, 这个方法不仅有相当的精确度, 而且使用简便 并具有更广泛的适用性, 对于 GA RCH 模型中运用格点法难以求解的浮动执行价格的美式亚式期权同样可 以得到稳定解. 关键词　蒙特卡罗模拟法, GA RCH 期权定价模型, 美式亚式期权 1. 引　言 除了少数情况, 金融衍生产品的定价一般必需通过数值计算才能解决, 而常用的数值计算 方法为蒙特卡罗模拟法, 二叉树法, 偏微分方程法及格点法. 人们通常认为如果一个期权的支 付函数是与路径相关的或问题中的状态变量的数目较多时, 使用蒙特卡罗模拟法较方便, 但前 提是它必须是欧式的, 即在到期日之前不可以提前执行. 这是因为我们在运用蒙特卡罗模拟法 时通常采用一种前向的算法, 即从现在出发向前模拟资产价格的路径到期权的最后到期日并 独立计算每条路径上期权的价值后加以平均. 而对于带有提前执行的性质的期权, 如美式期 权, 却一般需要倒向的算法来计算每个时点上继续持有这个期权的价值, 并将这个持有价值和 立即执行期权所得的收益比较来确定是否应该提前执行. 二叉树法, 偏微分方程法及格点法都 运用倒向的算法, 即从期权的到期日出发向后倒推计算得到期权现在的价格. 如果期权的支付 函数与路径无关, 问题中的状态变量的数目较少, 并且可以提前执行, 那么使用后三种方法一 般都能有效准确地求得期权的价值. 但是如果期权的支付函数与路径相关, 状态变量的数目较 多, 同时又具有提前执行的性质 (本文要考察的美式亚式期权就是这样一个例子) , 那么选用那 一个方法求解更方便呢? 如果问题不是很复杂, 状态变量的数目还不是很大的时候, 我们还可 以继续用二叉树法, 偏微分方程法及格点法求解, 但如果状态变量的数目超过三的话, 我们就 很难再用这些方法, 这是因为它们都会受所谓”维数灾难”(dim en sional cu rse) 的影响, 即使用 这些方法时, 计算量会随着问题维数的增加指数式地迅速增加. 和这些方法不同的是, 蒙特卡 罗模拟法的计算量随着问题维数只是线性地增加, 因此人们一直在寻找一种在蒙特卡罗模拟 法框架下处理提前执行的性质的方法. 显然有了这样的方法几乎所有的期权都能用蒙特卡罗 模拟法求解了. T illey [ 1 ]在 1993 年最先提出了一个用蒙特卡罗模拟法求解美式期权的方法, 他在B lack 收稿日期: 2003 10 18
    —241— 经　济　数　学　　　　　　　　　　　　　　　　第 21 卷　 Scho les 模型的框架下模拟股价的路径后, 在每个时间点上将所有的路径按照股价大小分组归 类, 股价相近的路径集中起来放在一个组里, 用同一组中路径样本来近似计算美式期权的持有 价 值. T illey 的 方 法 运 用 起 来 很 简 单, 但 精 确 度 不 高, 难 以 达 到 实 际 运 用 的 要 求. 之 后 B arraquand 和M artineau [ 2 ], B roadie 和 Glasserm an [ 3, 4 ], B raodie, Glasserm an 和 Jain [ 5 ], R aym ar 和 Zw echer [ 6 ]等人提出了不同形式的筛孔法来近似计算转移密度函数. Gran t, V o ra 和W eek s[ 7 ]等人则提出用有限个参数来确定美式期权的提前执行边界的方法, 通过对这些 参数进行最优化处理后计算期权的价值. 最近L ongstaff 和 Schw artz [ 8 ]提出用一组以状态变量为自变量的基函数来展开美式期 权计算中所需的继续持有的价值函数, 在每个时间点上利用所有路径上期权今后的价值根据 最小二乘法原理求得基函数的展开系数, 从而得到继续持有的价值函数. 在他们的论文中, L ongstaff 和 Schw artz 给出了用这个方法计算许多带有提前执行特点的金融衍生品的例子, 说明了这个方法的普遍适用性. Egloff 和M in- OO [ 9 ]从理论上也证明了这个方法的收敛性. 本文将运用L ongstaff 和 Schw artz 的方法在 GA RCH 模型中对美式亚式期权进行计算. 亚式期权是一种最常见的奇异期权, 有着广泛的实际应用, 和普通的期权不同的是当期权被执 行时, 我们不是用标的资产在执行日的价格, 而是用标的资产在包括执行日在内的一段时间内 的平均价格来计算其现金流量的. 美式亚式期权的数值计算问题很有特点, 一方面它的支付函 数与路径相关, 因而用二叉树法, 偏微分方程法及格点法求解都有一定的困难, 另一方面它又 具有提前执行的特点, 这是传统的蒙特卡罗模拟法难以处理的问题. 在B lack Scho les 模型的 框架下, H u ll 和W h ite [ 10 ]利用二叉树和格点方法做了一些研究工作,B arraquand 和 Pudet [ 11 ]及 Zvan, Fo rsyth 和V etzal[ 12, 13 ]分别用不同的方法来求解美式亚式期权所满足的偏微 分方程, Am eu r, B reton 和 L ’Ecuyer [ 14 ]提出了一个采用对亚式期权的价值函数进行分段多 项式近似, 按照动态最优化原理进行求解的数值方法. 然而在 GA RCH 模型中, 由于其状态变 量比 B lack Scho les 模型多了一个, 大大增加了运用二叉树法及格点法的难度 (GA RCH 模型 因是离散时间下的模型, 没有偏微分方程解法). 最近本文作者在[ 15 ]第一次提出了一个在 GA RCH 模型中运用格点法的数值求解美式亚式期权的方法. 但是这个格点法虽然可以用于 固定执行价格的亚式期权, 对于浮动执行价格的亚式期权的定价问题我们却发现很难找到合 适的格点分法来得到稳定的数值解. 一般说来, 基于蒙特卡罗模拟的算法都具有较好的稳定 S 所提出的方法能更有效地解决美式亚式期权的定价问题. 在下一节中 性, 因此我们希望L S 方法求解美式亚式期权的步骤, 然后举例验证 我们首先在B lack 这个方法的准确性. 尔后在第三节中我们讨论 GA RCH 模型中美式亚式期权的L S 蒙特卡罗 模拟算法. Scho les 模型中解释运用L 2. B-S 模型中的蒙特卡罗模拟算法 我们首先在B lack Scho les 模型中讨论美式亚式期权的计算. 我们假设存在一个风险中性 测度Q , 在这个测度下资产价格服从几何B row n 运动, 即: dS S = rd t + d z (1)
    　第 2 期　　　邵　斌　丁　娟　GA RCH 模型中美式亚式期权价值的蒙特卡罗模拟算法 —341— 其中 r 和 分别为无风险利率和波动率 由于美式亚式期权可以提前执行, 我们在求解其价值时需要在每个时间点上计算该期权 立即执行的情况下的执行价值 (exercise value) 和不立即执行的情况下的持有价值 (ho lding value) , 并取两者中较大的作为在该时点上的价值 根据美式亚式期权的支付函数, 我们可以 设在时间 t, 期权标的资产的价格为 S t, 按照期权合约所计算的 很容易地求得它的执行价值 资产的平均价值为 S t. 如果亚式期权的执行价格是固定的, 记为 K , 那么它的执行价值为: 　　其中对于看涨期权 么它的执行价值为: V e ( t) = m ax ( = 1, 而对于看跌期权 (S t - K ) , 0) (2) = - 1, 如果亚式期权的执行价格是浮动的, 那 V e ( t) = m ax ( (S t - S t) , 0) 　　相比之下, 持有价值的计算则要困难得多, 它的定义为: ) ] t)V e ( 是期权第一次被执行的时间, 它是一个随机变量. V h ( t) = E Q 其中 t [ e- r ( - (3) (4) 我们设现在的时间为 0, 期权到期日为 T. 为了进行模拟计算我们将这段时间分为N 个长 度相等的时间段, 0= t0< t1< …< tN - 1< tN = T , 其中 ti+ 1- 下面的步骤应用L ongstaff 和 Schw artz 的方法计算美式亚式期权: ti= T N , i= 0, 1, …, N - 1. 我们按照 第一步: 从现在的资产价格 S 0 出发, 我们根据 (1) 式模拟M 条资产价格的路径, S p i , 和相 i , 其中指标 p 代表第 p 条路径, p = 1, 2, …,M , 而 i 是时间指标, i= 0, 1, …, p 应的平均价格 S N . 第二步: 在到期日 T , 我们用 (2) 或 (3) 式求得期权的价值 V p N , 并将每条路径的执行时间都 取为: 　　第三步: 在时间 tN - 1, 我们选用所有执行价值大于零的路径, 假设共有L 条这样的路径, 指 标为 p 1, p 2, …, p L , 在每条路径上计算持有价值的现值: p N = T , p = 1, 2, …,M Y j = V h ( tN - 1) = exp (- r ( p jN - tN - 1) )V e p j ( tN ) , j = 1, 2, …, L (5) t, 我们取八个以这两个状态变量为自变量的基函数: 1, t) , k = 1, 2, …, 8. 在这 L 条路径上算出这些基函 这里的状态变量有两个, 即为 S t 和 S S t, S t , S 数的值得到 t 和 S tS 2 t , S tS t, S 2 tS t, S 2 2 t , 记为 X k (S t, S 并用最小二乘法求解回归方程: X j k = X k (S p jtN , S p jtN ) Y j = 8 k= 1 a kX j k　j = 1, 2, …, L (6) (7) 得到展开式中的系数 a 1, a 2, …, a 8 这时我们将根据以下的规则确定在所有M 条路径上, 期权 是否在时间 tN - 1执行: 对于执行价值等于零的路径, 期权不会在 tN - 1执行; 对于 L 条执行价值 大于零的路径, 我们用最小二乘法得到的函数 Y = 8 k= 1 a kX k (S t, S t) (8)
    —441— 经　济　数　学　　　　　　　　　　　　　　　　第 21 卷　 来重新计算期权的持有价值, 如果所得到的持有价值小于这条路径上的执行价值, 那么期权将 被执行; 如果所得到的持有价值大于这条路径上的执行价值, 期权则不会被执行 根据期权是 否被执行的判断, 我们得到 tN - 1时每条路径上的期权执行时间 N - 1: 如果第 p 条路径被执行, N - 1= tN - 1, 否则, p N - 1= p N. p p 第四步: 我们按照第三步的方法, 逐次向后倒推 i+ 1, 为了确定 ti 时的期权执行时间 设我们已经求得 ti+ 1时的每条路径上的 期权执行时间 i , 我们先选出所有执行价值大于零的路 径, 假设共有 L ’条这样的路径, 指标为 p 1, p 2, …, p L ’, 在每条路径上计算持有价值在 ti 的现 值: p p Y j = exp (- 和基函数在这些路径上的值 X j r ( p ji+ 1 - ti) )V e p j ( p ji+ 1) , j = 1, 2, …, L ’ k, 用最小二乘法求解回归方程 Y j = 8 k= 1 a kX j k (S t, S t) , j = 1, 2, …, L ’ (9) (10) p 表示根据上面回归函数计算得到的第 p 条路径的期权在 ti 时的持有价值, 我们有 如果用 V h 下面的关系: p < V h p = 0 或V e p i = ti 1) 如果 V e 2) 否则, 第五步: 重复第四步一直算到 t1, 我们便得到期权的价值: p , 则 p i+ 1 p i = V = 1 M M p = 1 r e- p 1V e p ( p 1 ) (11) 　　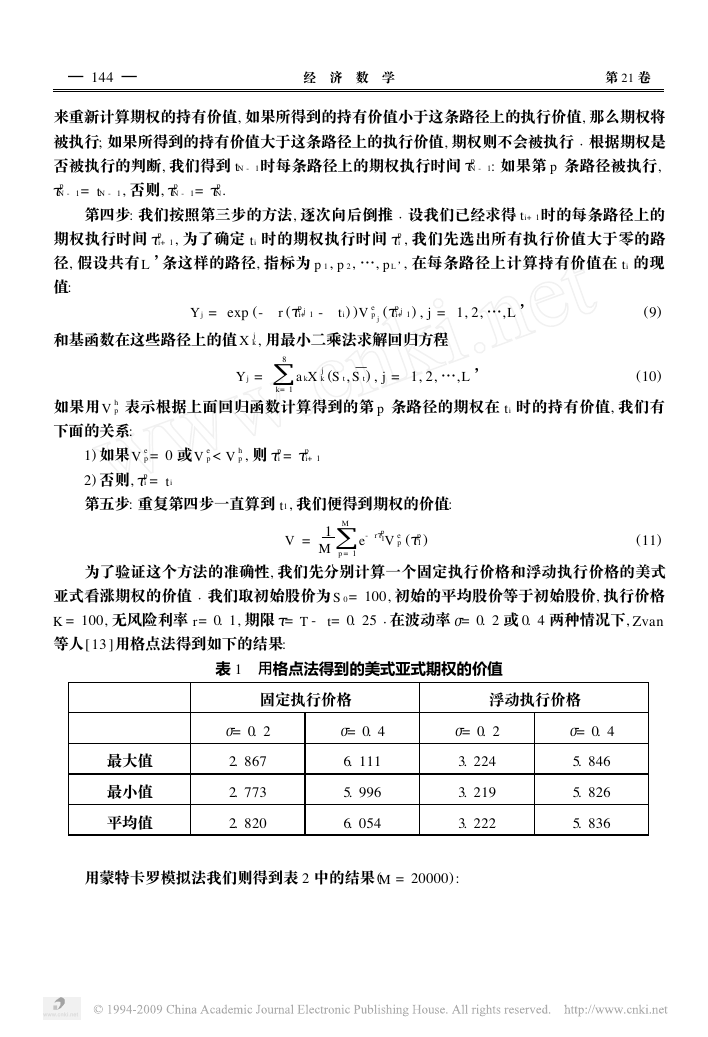为了验证这个方法的准确性, 我们先分别计算一个固定执行价格和浮动执行价格的美式 我们取初始股价为 S 0= 100, 初始的平均股价等于初始股价, 执行价格 亚式看涨期权的价值 K = 100, 无风险利率 r= 0. 1, 期限 = 0. 2 或 0. 4 两种情况下, Zvan 等人[ 13 ]用格点法得到如下的结果: 在波动率 t= 0. 25 = T - 表 1　用格点法得到的美式亚式期权的价值 固定执行价格 浮动执行价格 = 0. 2 2. 867 2. 773 2. 820 = 0. 4 6. 111 5. 996 6. 054 = 0. 2 3. 224 3. 219 3. 222 = 0. 4 5. 846 5. 826 5. 836 最大值 最小值 平均值 用蒙特卡罗模拟法我们则得到表 2 中的结果 (M = 20000) :
    　第 2 期　　　邵　斌　丁　娟　GA RCH 模型中美式亚式期权价值的蒙特卡罗模拟算法 —541— 表 2　用蒙特卡罗模拟法得到的美式亚式期权的价值 固定执行价格 浮动执行价格 = 0. 2 2. 810 = 0. 4 6. 050 = 0. 2 3. 196 = 0. 4 5. 788 将表 2 的结果跟表 1 中的平均值比较表明两种方法所得到的结果十分接近 我们可以看出无 论是计算固定执行价格的美式亚式期权还是浮动执行价格的美式亚式期权的价格, 两种方法 所得到的结果都十分接近. 这些例子说明蒙特卡罗模拟法可以用于B S 模型中美式亚式期权 的计算. 下面我们把这个方法推广到 GA RCH 期权定价模型中. 3. GARCH 模型中的蒙特卡罗模拟算法 D uan [ 13 ]在 1995 年第一次提出了一个在 GA RCH 模型框架下期权定价的完整理论, 他 运用均衡定价原理证明了当投资者的效用函数满足一定的条件时, 就存在一个满足局部风险 中性定价关系的概率测度Q , 在这个测度下资产收益率由下式给出: 其中 r 是无风险利率, t+ 1 ln S t+ 1 S t = r - 1 2 h t+ 1 + h t+ 1 t+ 1 Q ～ N (0, 1) , 也就是说在测度 Q 下, t (12) t+ 1是一个在时间 t 时的条件 分布为标准正态分布的随机变量. 因而在时间 t 时资产收益率的条件方差为 h t+ 1, 其变化则满 足下面的 GA RCH 过程: h t+ 1 = 0 + 1h t + 2h t ( t - - ) 2 (13) 其中 0> 0, 1 0, 2 0 和 都得 GA RCH 模型中的参数, 则是风险溢价率. 我们在 GA RCH 模型下可以运用同样的方法来计算美式亚式期权. 我们对上节所列的步 骤只要做下面两点修改就可以了: 1. 我们改用 (12) 和 (13) 式模拟资产价格的路径: 2. 由于 GA RCH 模型下每个时点上的状态变量有三个, 即 S t, S 个基函数来表示期权的持有价值函数: 1, S t, S h 3 th 2 t+ 1, S tS 2 t h t+ 1, S th 2 th t+ 1, S 2 tS t h t+ 1, S tS t+ 1, S t, S 2 2 t , S t, h t+ 1, S 2 t+ 1. t 和 h t+ 1, 我们取以下二十 3 t , t, S th t+ 1, S th t+ 1, S 3 t , S t , S 2 t , h 2 t+ 1, S tS 我们首先计算几个固定执行价格的美式亚式期权的价值, 并和文献[ 15 ]中用格点法所得 = 0. . 初始股价取为 S 0= 50, 执行价格 K = 50, 期权的期限公别为 结果进行比较. 作为例子我们取 GA RCH 模型的参数为 3, 30 天, 90 天和 180 天, 计算结果列于表 3 中, 在计算中取M = 20000. = 0. 2, 无风险年利率 r= 5 0= 0. 00001, 1= 0. 8, 2= 0. 8,
    —641— 经　济　数　学　　　　　　　　　　　　　　　　第 21 卷　 表 3　固定执行价格的美式亚式期权的价值 期限 30 天 90 天 180 天 蒙特卡罗模拟法 格点法 0. 780 1. 490 2. 242 0. 843 1. 558 2. 331 从表 3 中我们可以看到两种方法所得结果很接近, 但在实际使用时, 蒙特卡罗模拟法要比 格点法简便的多. 格点法不仅需要复杂的编程, 在使用过程中还需要我们认真选择合适的格点 才能保证得到精确的解. 我们在 GA RCH 模型中远用格点法来计算浮动执行价格的美式亚式 期权时则发现很难找到合适的格点分法来得到稳定的数值解, 而对于蒙特卡罗模拟法, 我们只 要将用于计算固定执行价格的美式亚式期权价值的程序稍加修改就可以用于浮动执行价格的 美式亚式期权而得到稳定的数值解, 相应的结果列在表 4 中. 表 4　浮动执行价格的美式亚式看涨期权的价值 期限 30 天 90 天 180 天 蒙特卡罗模拟法 0. 959 1. 835 2. 730 最后需要指出的是在所有用蒙特卡罗模拟法进行的计算中, 我们所取路径数均为M = 20000. 为了说明我们所得数值解的稳定性, 我们以表 4 中的 90 天期权为例, 取不同的路径数 重新计算, 结果列于表 5 表 5　路径数对期权的价值计算结果的影响 数径数M 90 天期权价 10000 16000 18000 20000 30000 40000 1. 864 1. 841 1. 836 1. 835 1. 837 1. 830 从表中结果可以看到, 当M = 20000 时, 期权价已经收敛了, 再增加路径数对期权价的影响不 超过 0. 01.
    2 2 —741— 2 2 2 2 　第 2 期　　　邵　斌　丁　娟　GA RCH 模型中美式亚式期权价值的蒙特卡罗模拟算法 4. 总结 带有提前执行性质的金融衍生产品 (如美式期权) 的价值计算一直是研究工作者和实务工 作者所关心的问题. 一般来讲, 这些产品的定价必需使用数值求解方法. 在诸多的数值方法中, 蒙特卡罗模拟法是最易使用, 稳定性最好的一种, 而且和其它方法不同的是它不受所谓维数灾 难的影响, 尤其适用于复杂的模型中期权定价问题. 然而通常在直接运用蒙特卡罗模拟法时人 们采用一种前向的算法, 而美式期权的计算需要倒向的算法, 因此在很长的一段时间里人们认 为蒙特卡罗模拟法不能用来计算美式期权. 最近L ongstaff 和 Schw artz 提出了运用蒙特卡罗模拟法求解美式期权的最小二乘算法, 受到人们特别是实务工作者的普遍关注, 许多过去由于模型和产品的复杂性而不能求解的美 式期权问题有可能在这种方法下得到解决. 本文用 GA RCH 模型中美式亚式期权的定价这样一个较为复杂的问题作为例子, 检验了 这种方法的适用性和准确性. 我们希望今后把这种方法运用到其它更复杂的模型和期权的定 价问题上. 参　考　文　献 [ 1 ] 　T illey J A. , V alu ing Am erican op tion s in a path sim u lation m odel[J ], T ransactions of the S ociety of A ctua ries, 45 (1993) , 83 104 [2 ] 　B arraquand J , M artineau D , N um erical valuation of h igh dim en sional m u ltivariate Am erican secu rities [J ], J ou rna l of F inancia l and Q uan tita tiv e A na ly sis, 30 (1995) , 383 405 [ 3 ]　B roadie M , Glasserm an P, P ricing Am erican- style secu rities u sing sim u lation [J ]. J ou rna l of E conom ic D y nam ics and C on trol, 21 (1997a) , 1323 1352 [ 4 ] 　B roadie M , Glasserm an P M on te Carlo m ethods fo r p ricing h igh dim en sional Am erican op tion s: an overview [J ]. 21 (1997b) , 1323 1352 [ 5 ] 　B roadie M , Glasserm an P, Jain G Enhanced M on te Carlo estim ates fo r Am erican op tion s p rices [J ], J ou rna l of D eriv a tiv es, 5 (1997) , 25 44 [ 6 ]　 R aym ar S, Zw echer M , A M on te Carlo valuation of Am erican call op tion s O n the m ax im um of several stock s[J ], J ou rna l of D eriv a tiv es, 5 (1997) , 7 23 [ 7 ]　 Gran t D , V o ra G W eek s D. Sim u lation and the early exercise op tion p rob lem [J ], J ou rna l of F inancia l E ng ineering , 5 (1996) , 211 227 [ 8 ]　L ongstaff F A , Schw artz E S, V alu ing Am erican op tion s by sim u lation: a sim p le least square app roach [J ], R ev iew of F inancia l S tud ies, 14 (2001) , 113 147 [ 9 ] 　Ego lff D an iel,M in [J ], P rep rin t, 2002. OO M aung, Convergence of M on te Carlo algo rithm s fo r p ricing Am erican op tion s [ 10 ]　H u ll J ,W h ite A , Efficien t p rocedu res fo r valu ing Eu ropean and Am erican path dependen t op tion s[J ], J ou rna l of D eriv a tiv es, 1 (1993) , 21 31. [ 11 ] 　B arraquand J , Pudet T , P ricing of Am erican path dependen t con tingen t claim s [ J ], M a them a tica l
    —841— 经　济　数　学　　　　　　　　　　　　　　　　第 21 卷　 F inance, 6 (1996) , 17 51 [ 12 ]　Zvan R P, Fo rsyth P A , V etzal K P, Robu st num erical m ethods fo r PD E m odels of A sian op tion s[J ], J ou rna l of C om p u ta tiona l F inance, 1 (1998) , 39 78. [13 ] 　Zvan R P, Fo rsyth P A , V etzal K R , D iscrete A sian barrier op tion s [J ], J ou rna l of C om p u ta tiona l F inance, 3 (1999) , 41 67 [ 14 ]　Am eu r H B , B reton M , L ’Ecuyer P, A num erical p rocedu re fo r p ricing Am erican style A sian op tion s, P rep rin t, 2000. [ 15 ]　邵斌, 丁娟, GA RCH 模型中美式亚式期权的数值解法[J ], 预测, 5 (2003) , 57- 65 M O NTE CARLO SIM ULAT IO N M ETHOD FO R PR IC ING AM ER ICAN-STYL E ASIAN O PT IO N IN THE GARCH O PT IO N PR IC ING M OD EL Shao B in　D ing Juan (Institu te of S ecu rities and F u tu res, S hang ha i U n iv ersity of F inance and E conom ics, S hang ha i, 200433, C h ina) Abstract　 W e u se the M on te Carlo sim u lation m ethod of L ongstaff and Schw artz to p rice Am erican A sian op tion s in the fram ew o rk of GA RCH op tion p ricing m odel. O u r resu lts dem on strate that th is m ethod style no t on ly has com parab le accu racy as o ther m ethods, bu t also can be im p lem en ted m o re easily w ith w ider app licab ility. In particu lar, th is m ethod can be u sed to ob tain stab le so lu tion s fo r floating- strike Am erican- style A sian op tion s fo r w h ich it is difficu lt to app ly lattice m ethod in the GA RCH op tion p ricing m odel. Key words　M on te Carlo sim u lation m ethod, GA RCH op tion p ricing m odel,Am erican style A sian op tion
    分享到：
    赞 收藏

    相关推荐

    资料库

    存储

    共收录294份资料，累计8个分类，关注成员有19位，主要包括：EMC,SUN,IBM,Dell,HP,Microsoft,Veritas,其它

    热门标签

    EMC SUN IBM Dell HP Microsoft Veritas 其它

    最新资料