logo资料库

核密度估计简略教案.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：4.22M 资料格式：doc 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
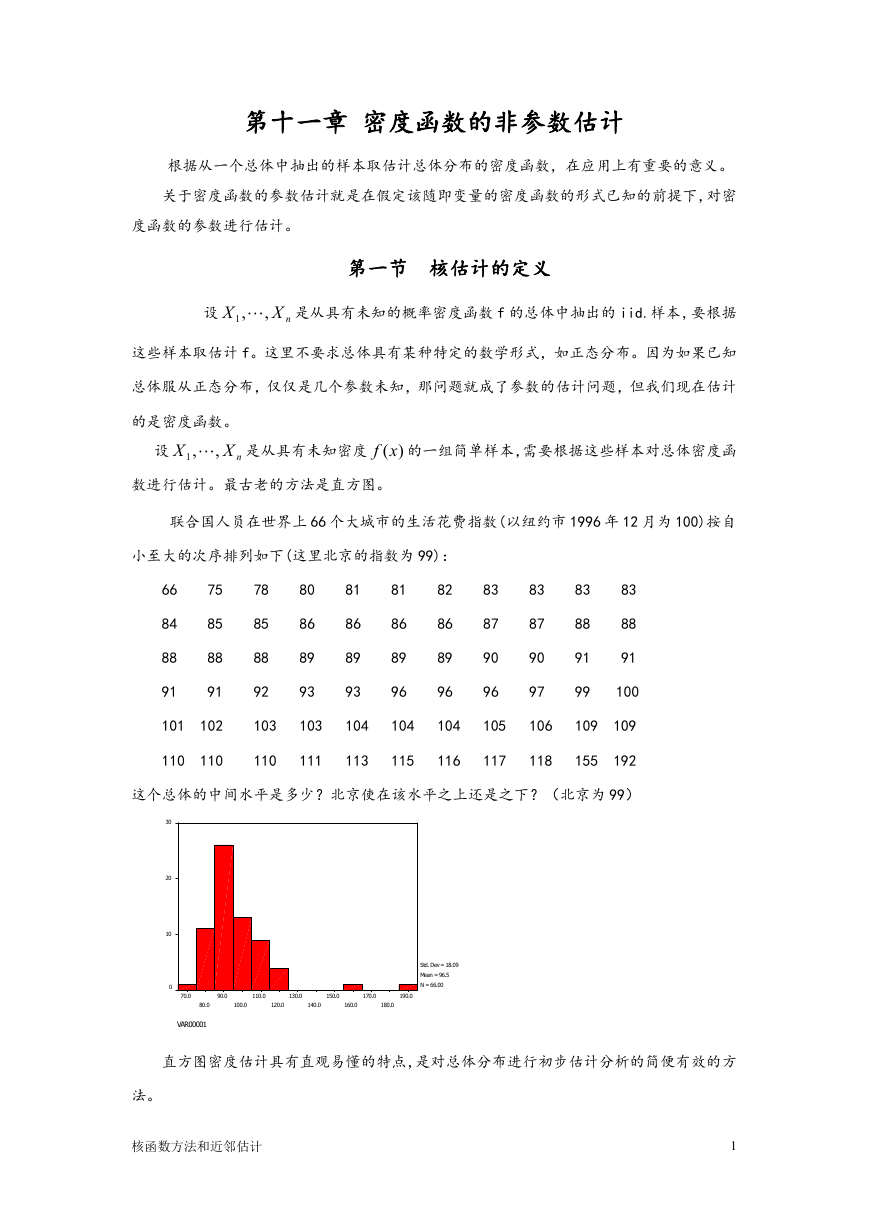
    第十一章 密度函数的非参数估计 根据从一个总体中抽出的样本取估计总体分布的密度函数，在应用上有重要的意义。 关于密度函数的参数估计就是在假定该随即变量的密度函数的形式已知的前提下，对密 度函数的参数进行估计。 第一节 核估计的定义 设 X ,1  是从具有未知的概率密度函数 f 的总体中抽出的 iid.样本，要根据 nX , 这些样本取估计 f。这里不要求总体具有某种特定的数学形式，如正态分布。因为如果已知 总体服从正态分布，仅仅是几个参数未知，那问题就成了参数的估计问题，但我们现在估计 的是密度函数。 nX X 设 ,1  是从具有未知密度 )(xf 的一组简单样本，需要根据这些样本对总体密度函 , 数进行估计。最古老的方法是直方图。 联合国人员在世界上 66 个大城市的生活花费指数(以纽约市 1996 年 12 月为 100)按自 小至大的次序排列如下(这里北京的指数为 99)： 66 84 88 91 75 85 88 91 78 85 88 92 80 86 89 93 81 86 89 93 81 86 89 96 82 86 89 96 83 87 90 96 83 87 90 97 83 88 91 99 83 88 91 100 101 102 103 103 104 104 104 105 106 109 109 110 110 110 111 113 115 116 117 118 155 192 这个总体的中间水平是多少？北京使在该水平之上还是之下？（北京为 99） 30 20 10 0 70.0 90.0 110.0 130.0 150.0 170.0 190.0 80.0 100.0 120.0 140.0 160.0 180.0 VAR00001 Std. Dev = 18.09 Mean = 96.5 N = 66.00 直方图密度估计具有直观易懂的特点，是对总体分布进行初步估计分析的简便有效的方 法。 核函数方法和近邻估计 1
    在做直方图时，区间的划分的方式需要根据实际情况或按经验来决定，一般，在 m 个区间 应该包含全部或绝大部分（比如 99%）的样本，而 m 的大小要根据样本容量而定。 为了克服直方图在区间中心部分估计较好，而在区间端点附近效果比较差的缺点，一种 改进的方法是核估计方法。核估计方法与直方图方法类似，核估计方法也计算某一点周围的 点的个数，只是对于近处的点考虑多一点，远处的点考虑少一点或不考虑。 首先以每个 X 为中心做区间 hXhX  ,  ，其中 h 是事先给定的区间半径，用 xn 记 为 X ,1  落在如此区间的样本点个数，用 nX , )(ˆ x f n  n x 2 hn 去估计密度函数 )(xf 。我们可 以把 )(ˆ x f n  n x 2 hn 看成为该小区域的频率密度。由于对某个区间的所有的 X 值，均以其为 中心构造区间。显然这种密度估计的效果优于直方图估计。具有良好的连续性。 设 )( xK  2/1   0  1 1 x  其它 ，则 )(xK 为 11， 区间上均匀分布的密度函数，而 X 2h )(ˆ x f n  1 nh n  i 1  k ( Xx  h i ) 在上式中，将 )(xK 换成任意一个概率密度就得到密度的核估计。 核函数方法和近邻估计 2
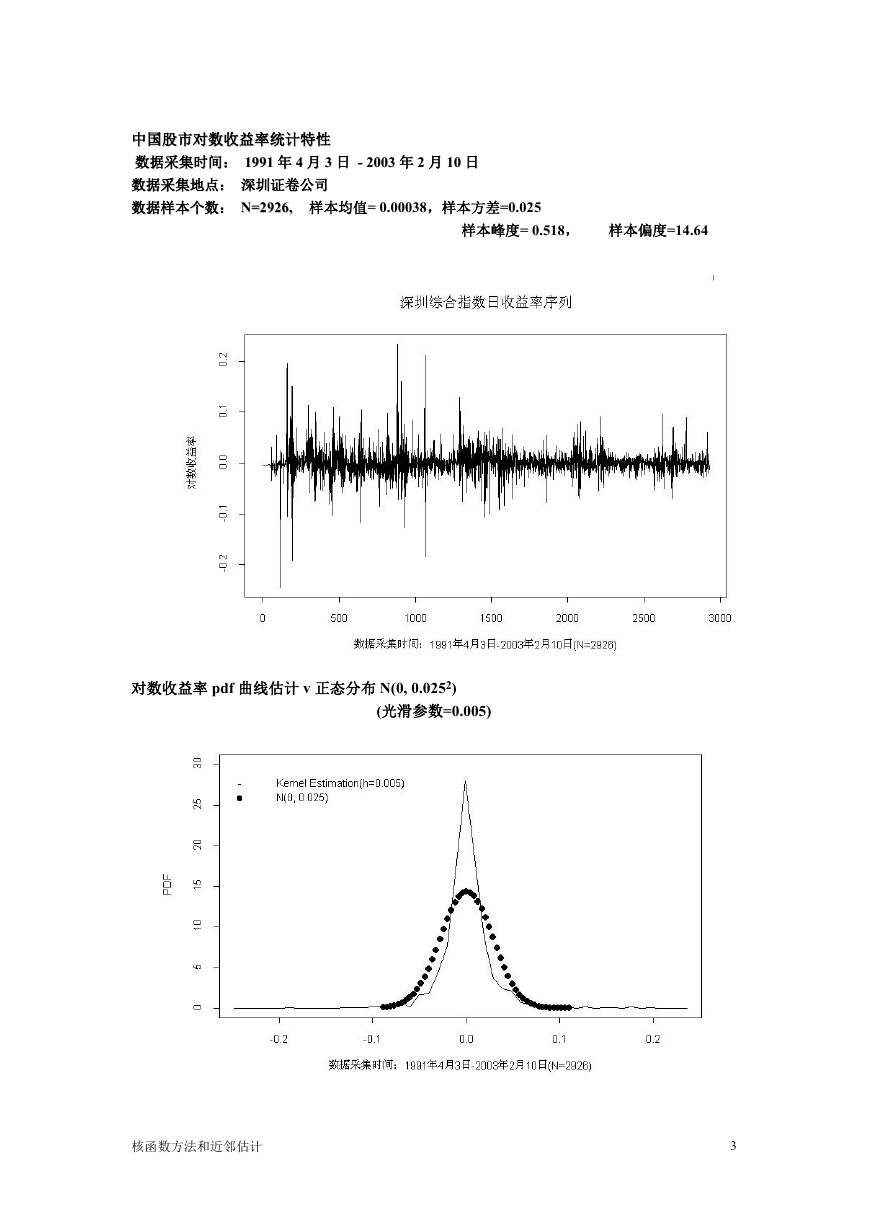
    中国股市对数收益率统计特性 中国股市对数收益率统计特性 1991 年年 44 月月 33 日日 -- 2003 数据采集时间： 1991 数据采集时间： 数据采集地点： 深圳证卷公司 深圳证卷公司 数据采集地点： N=2926, 样本均值= 0.00038，样本方差=0.025 数据样本个数： N=2926, 数据样本个数： 2003 年年 22 月月 1010 日日 样本峰度= 0.518， 样本偏度=14.64 对数收益率 pdf 曲线估计 v 正态分布 N(0, 0.0252) (光滑参数=0.005) 核函数方法和近邻估计 3
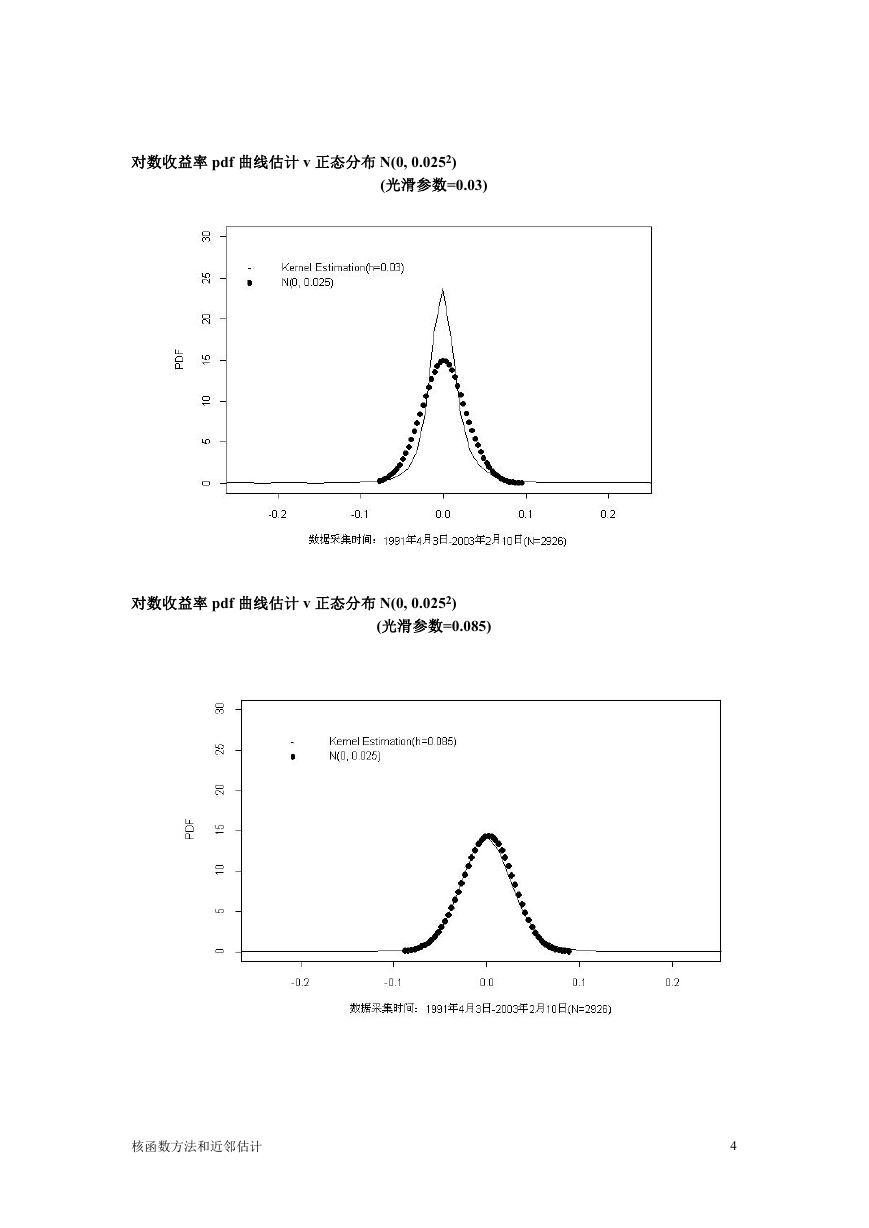
    对数收益率 pdf 曲线估计 v 正态分布 N(0, 0.0252) (光滑参数=0.03) 对数收益率 pdf 曲线估计 v 正态分布 N(0, 0.0252) (光滑参数=0.085) 核函数方法和近邻估计 4
    定义：设 )(xK 为一个概率密度函数， 0h 为给定的常数， )(xf 为总体的密度函数， 则 )(ˆ x f n  1 nh n  i 1  k ( Xx  h i ) 称为 )(xf 的核估计。其中函数 )(xK 称为核，常数 h 称为窗宽。 核函数通常满足对称性及 dx)x(k  1 ，采用在原点有单峰的密度函数。核密度估计的 实质是对样本点施加不同的权数，用加权来代替通常的记数，核函数即为权函数。该估计利 用数据点 ix 到 x 的距离 x  来决定 ix 在估计点 x 的密度时起的作用。离 x 越近的点加的权 ix 越大。 h 称为窗宽， h 越大，估计出的密度函数则越平滑。 在实际的应用中，常用的核函数为： 核函数的名称 核函数  x 均匀核 三角形核 )( uk  5.0   0  1 1 u  其它 )( uK  1(  u )  Epanechikov 核 )( uK   1(75.0 15 16 70 81 1((  1(  )( uK  )( uK   2u )  2 u u 2 ))  2  3) )( uK   2 u 2 e 1 2  1   2   ,0 cos( u ), 当 | u |   2 其它 四次核 六次方核 高斯核 余弦核 )( uK  窗宽 h 的大小与样本容量有关，太小和太大都不好。 二、核估计的大样本性质 1、核估计的渐近无偏性 设 ,1  是抽自均有密度函数 f 的总体的 iid.样本。 x nx , )(ˆ x f n  1 nh n  i 1  k ( Xx  h i ) 是 f 的渐近无偏估计，是指 )(ˆ x fE n lim n   )( xf 。 核函数方法和近邻估计 5
    2、核估计的均方相合性 设有核估计 n )(ˆ x f  fE n lim n  则称 )(ˆ x f n 是 f(x)的均方相合估计。 3、均方误差的渐近性态  1 nh n  i 1  k )(ˆ x  )( xf Xx  h i ) ，若对某个 x 有 (  2  )(ˆ x f n 必是弱相合的，即 0 )(ˆ x f n p  )( xf 。 现在要进一步求出均方误差的主要部分，由此可以对 nh 和 )(xK 的选择提供一些信 息。假定总体的密度函数 f 满足条件 概率密度函数，满足条件 f  在 )(x  , 上有界且处处连续。又设核函数 K 为 k 1 k 2       uK )( duu  0 2 duuKu )(  可以证明 MSE n f ( ( x ))   fE n )( x  2)( xf  1 4  f  )( x 2  2 hk 2 4 2  ( nh n )  2 f 2   )( x     2 duuK )( 2    高阶无穷小项 故上式主要部分是前两项之和。为了使其到达最小，应取  )( xf hn     2 duuK )( /( fk 2  ( x )) 2 51  51  n  cn  1 5 在前面推导中的条件满足的情况下，随着 n 的增加，估计量的偏差 MSE n f ( ( x )) 最多 可以用 54n 的速度收敛到零，而为了达到这个速度， nh 必须以 51n 的速度趋于零。 4、核估计的依概率一致收敛性 设有核估计 )(ˆ x f n  1 nh n n  i 1  k ( Xx  h n i ) 是以 K 为核的核估计，  n  n ( XX , 1 ,  , X 2 n )  sup x f n )( x  )( xf ，有 lim n  E n  0 核函数方法和近邻估计 6
    即  n  n ( XX , 1 ,  , X 2 n )  sup x f n )( x  )( xf 平均收敛到零。 三、窗宽的选择 窗宽 nh 越小，则核估计的偏差越小，但核估计的方差越大。反之，窗宽越大，则核估 计的方差变小，但核估计的偏差却增大，所以窗宽的变化不可能一方面使核估计的偏差变小， 同时又使核估计的方差降低。因而，最佳窗宽选择的标准必须在核估计的偏差核方差中进行 权衡，最佳的理论窗宽为 hn 51  cn ，c 是一个待估的常数。最佳的窗宽的选择在实际应用 中是不断地调整 c，使核估计达到满意的估计结果。 窗宽的选择通常采用交叉核实的方法。交叉核实法的思想是：用删除第 i 个观测的样本 数据集计算来求最佳的窗宽。 交叉核实比较严格，能说明所选择窗宽的有效性。 交叉核实可以检验所用窗宽是否稳定。 交叉核实可以解决样本容量不大的情形，改变样本，来检验方法是否稳定的问题。 具体的方法是：选择窗宽使得 h ISE n ( )          为最小。等价于 因为  所以  )(ˆ xfE )(ˆ xfE  )(ˆ xf  )(ˆ x f 2 dx )(ˆ 2 x f dx  )(ˆ )( xfxf  dx 2)( xf )( f x  2  )(ˆ2  dx dx  )(ˆ2  )( xfxf dx )( xfxf dx 最小。 )(ˆ )( xfxf dx 的无偏估计为 1 n  n 1 i  (ˆ i Xf  ) i 其中 if  ˆ 是将第i 个观测点剔除后的估计。不难推出 2 )(ˆ x f dx  2  hn  n 2  n n  i 1  j 1  x X K (  x n i h ) K ( X i h  x n ) dx  2  hn  n 2 n n  i 1  j 1  t X K (  x n i h  )( ) tKt dt 于是，交错鉴定法实际上是选择 nh 使 核函数方法和近邻估计 7
    ISE ( h ) 1 n  2  hn  n 2 n n  i 1  j 1  t X K (  x n i h  )( ) tKt dt  2 n 1  n  i 1  (ˆ Xf  i ) i 达到最小。 第二节 密度函数近邻密度估计 定义：设 X ,1  为取自一维连续分布的简单样本，对指定的实数 x 及正整数 k ，设 nX , kRX 为距 x 第 k 个最近的样本点，令 )(ˆ x f n  k  |2 Xxn | kR 则称 )(ˆ x f n 为总体密度函数 )(xf 的近邻密度估计。 近邻密度估计核均匀核估计相比，前者在各处估计的精度有较好的一致性，即在各处 的估计精度差别不大，而后者在样本密集的地方估计精度高，在样本稀疏的地方则估计精度 差。 在近邻估计中，入选的近邻样本点数 k 的选择是一个关键，理论上要求 n 和 k ，建议可以先选 k  。 n 将两种方法相结合，可以得到一种推广的形式 )(ˆ x f n  1  Xxn | | R x n  i 1  K ( | Xx  Xx  i ) | x R 其中 kRX 为距 x 第 k 个最近的样本点， )(xK 称为核。 kRXx  为窗宽，但是变化的。 在某些条件成立的情况下，近邻估计是渐近无偏的，依概率收敛。 定义：设  X ,1  ,  nX 是取自 p 维连续总体的简单样本， )(xK 为 p 维密度函数， 0h 为常数，总体密度函数的一个核估计可以表示为： )(ˆ f x n  1 nh p n  i 1  K ( Xx  h i ) 核函数方法和近邻估计 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料