第1页 / 共24页
第2页 / 共24页
第3页 / 共24页
第4页 / 共24页
第5页 / 共24页
第6页 / 共24页
第7页 / 共24页
第8页 / 共24页
Matlab软件包与Logistic回归.doc
Matlab 软件包与 Logistic 回归
在回归分析中，因变量 y 可能有两种情形：（１） y 是一个定量的变量，这
时就用通常的 regress 函数对 y 进行回归；（２）y 是一个定性的变量，比如，y
０或１，这时就不能用通常的 regress 函数对 y 进行回归，而是使用所谓的 Logistic
回归。
Logistic 回归的基本思想是，不是直接对 y 进行回归，而是先定义一种概率
函数，令
Pr
Y
1|
X
1
x X
1
,
2
x
2
,
,
X
n
x
n
1 。此时，如果直接对进行回归，得到的回归方程可能不满足这个
1 。直接求的表达式，是比较困难的一件
要求 0
条件。在现实生活中，一般有 0
事，于是，人们改为考虑
1
y
y
1
的概率
1
的概率
k
一般的， 0 k 。人们经过研究发现，令
Pr
Y
1|
X
1
x X
1
,
2
x
2
,
,
X
n
x
n
1
b X
1
b X
n
n
1
1
a e
a
0,
b
j
0
即，是一个 Logistic 型的函数，效果比较理想。于是，我们将其变形得到：
log
1
b
0
b x
1 1
b x
n n
然 后 ， 对
1
log
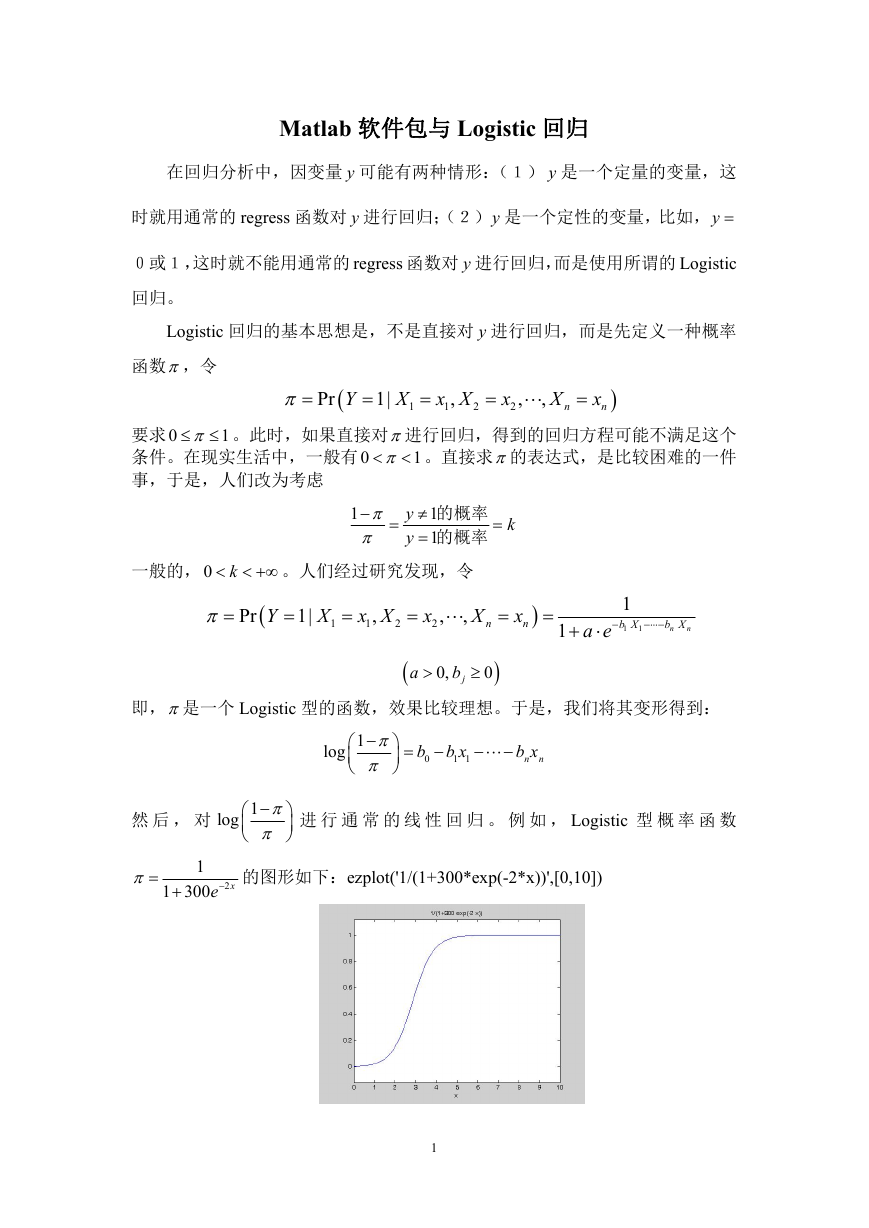
进 行 通 常 的 线 性 回 归 。 例 如 ， Logistic 型 概 率 函 数
1
1 300
2
xe
的图形如下：ezplot('1/(1+300*exp(-2*x))',[0,10])
1
例１ 企业到金融商业机构贷款，金融商业机构需要对企业进行评估。例如，
Moody 公司就是 New York 的一家专门评估企业的贷款信誉的公司。设：
2
2
下面列出美国 66 家企业的具体情况：
Y
X1
X2
y
企业 年后破产
0,
1
，企业 年后具备还款能力
X3
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
-62.8
3.3
-89.5
-3.5
-120.8
-103.2
-18.1
-3.8
-61.2
-20.3
-194.5
20.8
-106.1
-39.4
-164.1
-308.9
7.2
-118.3
-28.8
-50.6
-56.2
-17.4
-25.8
-4.3
-22.9
-35.7
-17.7
-65.8
-22.6
-34.2
-185.9
-280.0
-34.6
-27.9
-48.2
-49.2
-19.2
-18.1
-98.0
-129.0
-4.0
-8.7
-59.2
-13.1
-38.0
-57.9
-8.8
-64.7
-11.4
43.0
47.0
-3.3
35.0
-19.4
6.3
6.8
-17.2
-36.7
-6.5
-20.8
-14.2
-15.8
-36.3
-12.8
-17.6
1.6
0.7
-9.1
-4.0
4.8
16.4
16.0
4.0
20.8
1.7
1.1
2.5
1.1
0.9
1.7
1.0
0.5
1.0
1.5
1.2
1.3
0.8
2.0
1.5
6.7
3.4
1.3
1.6
0.3
0.8
0.9
1.7
1.3
2.1
2.8
2.1
0.9
1.2
0.8
0.9
0.1
0.9
1.3
1.9
2.7
1.9
2
46.7
20.8
33.0
26.1
68.6
37.3
59.0
49.6
12.5
37.3
35.3
49.5
18.1
31.4
21.5
8.5
40.6
34.6
19.9
17.4
54.7
53.5
35.9
39.4
53.1
39.8
59.5
16.3
21.7
12.6
12.5
23.6
10.4
13.8
33.4
23.1
23.8
7.0
34.1
4.2
25.1
13.5
15.7
-14.4
5.8
5.8
26.4
26.7
12.6
14.6
20.6
26.4
30.5
7.1
13.8
7.0
20.4
-7.8
0.9
2.4
1.5
2.1
1.6
3.5
5.5
1.9
1.8
1.5
0.9
2.6
4.0
1.9
1.0
1.5
1.8
1.8
2.3
1.3
1.7
1.1
2.0
1.9
1.9
1.2
2.0
1.0
1.6
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
其中，
X
1
未分配利润
总资产
X
2
支付利息前的利润
总资产
X
3
销售额
总资产
建立破产特征变量 y 的回归方程。
解：在这个破产问题中，
1
y
y
1
的次数
1
的次数
1
我们讨论
1
log
，概率 0,1 。设＝企业２年后具备还款能力的概率，即，
＝企业不破产的概率。因为 66 个数据有 33 个为 0，33 个为 1，所以，取分界
值 0.5，令
3
y
0,
1,
0.5
0.5
由 于 我 们 并 不 知 道 企 业 在 没 有 破 产 前 概 率 的 具 体 值 ， 也 不 可 能 通 过
1 2 3 的数据把这个具体的概率值算出来，于是，为了方便做回归运算，
,
X X X
,
我们取区间的中值， 0
0.25
-62.8
-89.5
y
X1
X2
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.75
0.75
3.3
-3.5
-120.8
-103.2
-18.1
-3.8
-61.2
-20.3
-194.5
20.8
-106.1
-39.4
-164.1
-308.9
7.2
-118.3
-28.8
-50.6
-56.2
-17.4
-25.8
-4.3
-22.9
-35.7
-17.7
-65.8
-22.6
-34.2
-185.9
-280.0
-34.6
-27.9
-48.2
-49.2
-19.2
-18.1
-98.0
-129.0
-4.0
-8.7
-59.2
-13.1
-38.0
-57.9
-8.8
-64.7
-11.4
43.0
47.0
-19.4
6.3
6.8
-17.2
-36.7
-6.5
-20.8
-14.2
-15.8
-36.3
-12.8
-17.6
1.6
0.7
-9.1
-4.0
4.8
16.4
16.0
对应
0.25;
y
1,
对应
0.75
。数据表变为：
X3
1.7
1.1
2.5
1.1
0.9
1.7
1.0
0.5
1.0
1.5
1.2
1.3
0.8
2.0
1.5
6.7
3.4
1.3
1.6
0.3
0.8
0.9
1.7
1.3
2.1
2.8
2.1
0.9
1.2
0.8
0.9
0.1
0.9
1.3
1.9
4
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
0.75
-3.3
35.0
46.7
20.8
33.0
26.1
68.6
37.3
59.0
49.6
12.5
37.3
35.3
49.5
18.1
31.4
21.5
8.5
40.6
34.6
19.9
17.4
54.7
53.5
35.9
39.4
53.1
39.8
59.5
16.3
21.7
4.0
20.8
12.6
12.5
23.6
10.4
13.8
33.4
23.1
23.8
7.0
34.1
4.2
25.1
13.5
15.7
-14.4
5.8
5.8
26.4
26.7
12.6
14.6
20.6
26.4
30.5
7.1
13.8
7.0
20.4
-7.8
2.7
1.9
0.9
2.4
1.5
2.1
1.6
3.5
5.5
1.9
1.8
1.5
0.9
2.6
4.0
1.9
1.0
1.5
1.8
1.8
2.3
1.3
1.7
1.1
2.0
1.9
1.9
1.2
2.0
1.0
1.6
于是，在 Matlab 软件包中编程如下，对
1
log
进行通常的线性回归：
X=[1,-62.8,-89.5,1.7;
1,3.3,-3.5,1.1;
1,-120.8,-103.2,2.5;
1,-18.1,-28.8,1.1;
1,-3.8,-50.6,0.9;
1,-61.2,-56.2,1.7;
1,-20.3,-17.4,1;
1,-194.5,-25.8,0.5;
1,20.8,-4.3,1;
1,-106.1,-22.9,1.5;
5
1,-39.4,-35.7,1.2;
1,-164.1,-17.7,1.3;
1,-308.9,-65.8,0.8;
1,7.2,-22.6,2.0;
1,-118.3,-34.2,1.5;
1,-185.9,-280,6.7;
1,-34.6,-19.4,3.4;
1,-27.9,6.3,1.3;
1,-48.2,6.8,1.6;
1,-49.2,-17.2,0.3;
1,-19.2,-36.7,0.8;
1,-18.1,-6.5,0.9;
1,-98,-20.8,1.7;
1,-129,-14.2,1.3;
1,-4,-15.8,2.1;
1,-8.7,-36.3,2.8;
1,-59.2,-12.8,2.1;
1,-13.1,-17.6,0.9;
1,-38,1.6,1.2;
1,-57.9,0.7,0.8;
1,-8.8,-9.1,0.9;
1,-64.7,-4,0.1;
1,-11.4,4.8,0.9;
1,43,16.4,1.3;
1,47,16,1.9;
1,-3.3,4,2.7;
1,35,20.8,1.9;
1,46.7,12.6,0.9;
1,20.8,12.5,2.4;
1,33,23.6,1.5;
1,26.1,10.4,2.1;
1,68.6,13.8,1.6;
1,37.3,33.4,3.5;
1,59,23.1,5.5;
1,49.6,23.8,1.9;
1,12.5,7,1.8;
1,37.3,34.1,1.5;
1,35.3,4.2,0.9;
1,49.5,25.1,2.6;
1,18.1,13.5,4;
1,31.4,15.7,1.9;
1,21.5,-14.4,1;
1,8.5,5.8,1.5;
1,40.6,5.8,1.8;
6
1,34.6,26.4,1.8;
1,19.9,26.7,2.3;
1,17.4,12.6,1.3;
1,54.7,14.6,1.7;
1,53.5,20.6,1.1;
1,35.9,26.4,2;
1,39.4,30.5,1.9;
1,53.1,7.1,1.9;
1,39.8,13.8,1.2;
1,59.5,7,2;
1,16.3,20.4,1;
1,21.7,-7.8,1.6];
a0=0.25*ones(33,1);a1=0.75*ones(33,1);
y0=[a0;a1];
Y=log((1-y0)./y0);
[b,bint,r,rint,stats] =regress(Y,X)
rcoplot(r,rint)
执行后得到结果：
b =
0.3914
-0.0069
-0.0093
-0.3263
0.0073
-0.0105
-0.0156
-0.5253
bint =
r =
0.7755
-0.0032
-0.0030
-0.1273
-0.0037
1.0561
-0.2683
0.6733
0.5028
0.3179
0.7320
-0.7044
1.1361
0.2553
0.4955
-0.1593
-1.7643
1.1984
0.0662
7
-0.9937
1.3983
0.9988
0.9621
0.3072
0.4942
0.8161
0.3957
0.1141
1.2176
1.2225
0.8670
0.7468
0.8531
0.5777
0.8556
0.2588
0.9675
-0.6179
-0.3984
-0.5943
-0.4360
-0.7585
-0.4476
-0.5541
-0.5288
-0.3687
0.2194
0.9248
-0.3078
-0.7516
-0.4266
-0.9150
-0.0680
0.0653
-0.5082
-1.1506
-0.8882
-0.5701
-0.4191
-0.3540
-0.8289
-0.4239
-0.5720
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
