logo资料库

声光光纤模式耦合的分析.pdf

发布时间：2022-06-14 发布人：admin 分类：说明书 资料大小：0.45M 资料格式：pdf 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    2 2 Ξ 第 7 卷 第 6 期 　 　　　　　　　　　 　　　上 海 大 学 学 报 (自 然 科 学 版) 　　　　 　 　　　　　 V o l. 7, N o. 6 2001 年 12 月　 　 　 　　　　　　JOU RNAL O F SHAN GHA I UN IV ER S IT Y (NA TU RAL SC IEN CE) 　　　　　　　　　　 D ec. 2001 文章编号: 1007 2861 (2001) 06 0481 06 声光光纤模式耦合的分析 肖彦萍, 　吴亚明, 　薛时光 (上海大学 通信与信息工程学院, 上海 200072) 摘要: 光纤声光器件是基于光纤中的超声光栅引起的两个光波同向模式间的耦合. 此文比较了声切变波和疏密波 激发的光纤超声光栅对双模光纤中对称模 L P 01、非对称模 L P 11间模式耦合的影响, 得到一个重要结论: 除了光纤超 声光栅的周期必须满足这两个耦合模式间的相位匹配条件外, 该光纤超声光栅还必须要破坏这两个模式间径向电 场的正交性. 这一结论为光纤声光器件控制光纤超声光栅产生有效的模式耦合提供了理论依据. 关键词: 模式耦合; 光纤声光器件; 光纤超声光栅 中图分类号: TN 25　　文献标识码: A Ana lysis of Acousto-O ptic F iber M ode Coupl ing X IAO Yan p ing, 　W U Ya m ing, 　XU E Sh i guang (Schoo l of Comm un ication and Info rm ation Engineering, Shanghai U n iversity, Shanghai 200072, Ch ina) Abstract: F iber acou sto op tic devices are based on coup ling betw een tw o cop rop agating m odes cau sed by u ltrason ic grating in the fiber. T he differen t fiber u ltrason ic gratings m ade of acou stic in the differen t m ode coup ling betw een L P 01 and L P 11 tran sverse and longitudinal w ave resu lt m odes w ith differen t p rop erties. T h is leads to an im po rtan t resu lt, in o rder to m ake the tw o m odes coup le effectively, the fiber u ltrason ic grating m u st distu rb the o rthogonality betw een the tw o m odes in addition to the p hase m atch condition. A cco rding to the resu lt, the fiber u ltra son ic grating cau sed by u ltrason ic w ave in the fiber can be selected to ach ieve effective coup ling of the tw o fiber Key words: m ode coup ling; fiber acou so op tic device; fiber u ltrason ic grating op tic m odes. that is, 　　全光透明的波分复用 (W DM ) 光纤通信网被广 泛认为是未来信息高速公路的骨干通信网, 而波长 选择性器件因其对波长具有分辨和选择能力在 W DM 系统中起着基本而重要的作用, 具有潜在、广 泛的应用前景. 波长选择性器件大都是基于模式耦 合机制, 例如光纤频移器[ 1～ 4 ]、光纤光栅滤波器[ 5～ 8 ]、 下线复用器 (ADM ) [ 9～ 10 ]、光路由开关[ 11～ 15 ]和光 上 纤可调谐滤波器[ 16～ 19 ]等等. 光纤声光器件可任意调 谐至所需的波长通道, 实现多个波长被同时且独立 地操作, 因而是实现W DM 光网络的关键器件, 也 被广泛认为是最有希望的多波长器件. 目前它已成 为W DM 光通信研究的热点, 有很多这方面的研究 报道. 光纤声光器件利用超声波在光纤纤芯中传播产 收稿日期: 2000 11 05　基金项目: 国家自然科学基金 (69777014) 资助项目; 上海科委启明星 (98QD 14020) 资助项目 　作者简介: 肖彦萍 (1974～ ) , 女, 湖南衡阳人, 硕士生, 主要从事W DM 光纤通信网络、全光网技术、光无源器件方面的研究.
    3Μ Λ Λ Μ ·284·　　　　　　　　　　　　　　　　 　 上 海 大 学 学 报 (自 然 科 学 版) 　　　　　　　　　　　　 　　第 7 卷 生光纤超声光栅, 补偿在同一光纤中传播的L P 01、 L P 11两个耦合模式间的传播常数差, 使得满足由光 纤超声光栅决定的相位匹配条件的两个模式之间发 生耦合, 产生能量交换, 从而实现波长的调谐和选 择. 光纤既是光波传输介质, 又是声波传输介质, 声 波与光波在同一光纤传输中发生相互作用. 由于多 个独立的光纤超声光栅在声光互作用区中可以同时 存在、相互叠加而不会互相干扰, 这样使得它可同 时、独立开关多个波长通道且波长可任意选择, 波长 调谐范围宽 (1. 2～ 1. 6 m ). 目前研究的声光器件 主要有两种: 一种为集成波导型的, 这种器件经过多 年的研究和发展, 技术已经比较成熟, 但是由于与通 信光纤耦合时的插入损耗很大、成本高, 影响其在光 纤通信系统中的应用; 另外一种是全光纤声光器件, 例如光纤声光频移器、光纤声光可调谐滤波器、光纤 路由开关和光纤上 下复用器 (ADM ) 等. 由于全光 纤型器件具有插入损耗小、能与通信光纤兼容、工艺 简单、体积小等优点, 已成为目前研究的热点. 本文通过研究基于模式耦合的光纤声光器件, 比较分析了不同模式的超声波 (剪切声波与疏密声 波) 在双模光纤中产生的光纤超声光栅对光波模式 耦合的影响. 着重分析了疏密声波产生的光纤超声 光栅, 与研究得较成熟的剪切声波产生的光纤超声 光栅做了比较, 从而得到一个重要的结论: 对称模与 非对称模之间的耦合除了必须满足相位匹配条件 外, 引起模式耦合的光纤超声光栅还必须破坏这两 个模式电场的正交性, 使得这两个传播模式电场不 再正交, 从而产生模式间的耦合. 1　激发光纤超声光栅的声波模式对光 波模式耦合的影响 光纤中任意两个模式间的耦合系数 k , 可以用 这两个模式的电场的空间矢量重积分来描述[ 20 ]: k = ∫D (n 2 - n 2 0) E E dA , (1) , E 分别为发生耦合的两个模式的电场分布, D 0 为由外界影响而产 E 为耦合叠加积分的面积, n 2- n 2 生的折射率扰动. 1. 1　切变声波激发的超声光栅及其引起的光波模 式耦合 在双模光纤中, 两个耦合模L P 01、L P 11之间的耦 合机理是在光纤中传播的切变声波会引起光纤周期 性的弯曲. 图 1 为光纤周期性弯曲的几何示意图, 耦 合系数 k 可以用下式表示[ 21 ]: k = E 0 ( r) exp j 2 n (1 - ) r co s , E 1 ( r, ) r d rd (2) 其中, E 0 ( r) 是 L P 01的电场分布, 指数项为由微弯引 起的空间相位畸变, E 1 ( r, ) 是 L P 11的电场分布, 且 满足 E 1 ( r, 是单个微弯的弯曲 [ 21 ]. ) = E 1 ( r) co s 角度 (假设为一很小值) , 为光纤受扰后总的幅度 变化, 系数 (= 0. 22) 为由光纤弯曲造成的拉伸而 产生的折射率变化的修正系数[ 22 ]. 图 1　光纤周期性弯曲的几何示意图 F ig. 1　Geom etry of fiber sub ject to periodic m icrobending 从式 (2) 中可以看到由于光纤受切变声波的激 发产生了周期性的微弯形变. 在切变声波的振动平 面内存在微弯形变, 而在垂直于振动平面内不存在 微弯形变, 即两个垂直平面内产生的扰动是不对称 的, 因而这种扰动的不对称性破坏了L P 01、L P 11之间 的正交性, 产生了径向方向上的变化, 即积分项中的 指数项 (与 co s 有关). 在没有扰动时,L P 01、L P 11之 间的电场是正交的, 其交叠积分为零, 而受到扰动 后, 式 (2) 的交叠积分结果不为零, 这就表明原本正 交的模式L P 01、L P 11之间产生了耦合, 发生了能量的 交换. 式 (2) 可以进一步简化为[ 21 ] k = 2 2n (1 - ) 4 L B ∫E 0 ( r) E 1 ( r) r2d r ≈ 2a, (3) 式中, L B 为 L P 01、L P 11模式间的拍差, a 为光纤的纤 芯半径. 由于光纤受切变声波激发的超声光栅产生 周期性的微弯形变, 导致了 L P 01、L P 11 模式间的耦 合. 从式 (3) 可以看到, 切变声波激发的超声光栅能 使L P 01、L P 11产生有效的耦合, 并且耦合强度与外部 切变声波的幅度大小 1. 2　声疏密波激发的超声光栅及其引起的光波模 成正比. 式耦合 当在光纤中传播的超声疏密波造成介质的局部 压缩和伸长时, 将产生光弹效应, 使得纤芯的折射率 发生变化. 因此, 在纤芯中形成周期性的折射率的变 化, 其作用结果相当于超声相位光栅, 其周期等于声
    3 ·384· p 12) , (9) n = 1 4 n 3S 3 (p 11 - ∃ ∃ 第 6 期　　　　　　　　　　　　　　　　肖彦萍, 等: 声光光纤模式耦合的分析 波的周期, 图 2 为光纤受到超声疏密波产生形变的 几何示意图, 其中虚线表示为光纤纤芯, 为超声疏 密波的周期. 在只考虑声疏密波作用的情况下, 光纤 被迫产生纵向应变, 使光纤的折射率发生纵向变化, 由光纤的光弹效应引起的折射率变化可表示为[ 23 ] B ij = 1 n 2 ij = p ij k lS k l, (4) ( i, j , k , l = 1, 2, 3) B ij为逆介电张量的增量, S k l为应变张量, p ijk l 式中, 为弹光系数张量. 考虑到应变张量 S k l和介质的逆介 电张量 B ij 的增量均为对称的二阶张量, 因此式 (4) 可以缩标表示为 B m = 1 n 2 m = p m nS n, (m , n = 1, 2, …, 6) (5) 图 2　光纤受纵向压缩后形变的示意图 F ig. 2　D iagram of fiber sub ject to periodic longitudinal strain 由弹性力学可知, 对于均匀的各向同性介质, 弹 光系数张量用矩阵表示为 p 11 p 12 p 12 p 11 p = p 12 0 0 0 p 12 0 0 0 式中, p 44= (p 11- p 12) 由式 (4) 和 (6) 得 0 0 0 p 44 0 0 0 0 0 0 p 44 0 0 0 0 0 0 p 44 p 12 p 12 p 11 0 0 0 2. , (6) B 1 = B 2 = B 3 = 1 n 2 1 n 2 1 n 2 1 2 3 = p 11S 1 + p 12S 2 + p 12S 3, = p 12S 1 + p 11S 2 + p 12S 3, (7) = p 12S 1 + p 12S 2 + p 11S 3, 式中, S 1、S 2 为光纤的径向应变 (S 1= S 2) , S 3 为光纤 的纵向应变 (S 3 = L ) , p m n 为弹光系数张量. 将 (7) 式代入 (8) 式中 L n = - 1 2 n 3 B , (8) 可得沿光纤纵向传播光相应的折射率变化, 即 式 (9) 是从光纤内部受扰动后的光弹效应产生的折 射率变化. 假设由声疏密波引起的光纤超声光栅折射率分 布为余弦分布, 可以得到纤芯折射率分布的表达式 为[ 24 ] n (z ) = n 0 + co s 2 z , (10) 式中, n 0 为没有受到扰动前的折射率, 光栅的调制强度参数, 于光纤超声光栅有 纤超声光栅, 则折射率的平方为 为光纤超声 为光纤超声光栅的周期. 对 1, 采用微扰理论[ 20 ]来分析光 n 2 (z ) n 2 0 + 2n 0 co s 2 z = n 2 0 + n ’, (11) n ’(= n 2- n 2 0) 为折射率的微扰项. 比较式 (9) 与 (11) , 可以看到两者的折射率变化 均是由同样的纵向压缩拉伸扰动引起的, 由此可以 得到调制强度 应当等于由光弹效应引起的折射率 的变化项, 即可得 = 1 4 n 3 (p 11 - p 12) S 3. (12) 将式 (12) 代入 n ’= 2n 0 co s 2 z 中, 可得: n ’= 1 2 n 0n 3 (p 11 - p 12) S 3 co s 2 z . (13) 　　依据公式 (1) , 可以得到由声疏密波产生的伸缩 变化而引起的L P 01、L P 11模式间的耦合系数 k 为 k =∫D (n 2 - n 2 0) E 0E 1 dA = n ’E 0 ( r) exp ( j 01z ) (14) E 1 ( r) co s exp (- j 11z ) r d rd . 　　从式 (13) 中可以看出, 由声疏密波引起的折射 n ’与由光弹效应产生的纵向应变 S 3 成 率变化项 正比, 即由声疏密波引起超声光栅的折射率变化是 沿光波传播方向的变化, 而在光纤圆周方向上的变 化是对称的, 所以并没有破坏对称模L P 01与非对称 模 L P 11径向电场之间的正交性. 这就导致了式 (14) 中的扰动项 n 并未产生径向方向上的变化, 使得 对称模 L P 01与非对称模 L P 11径向电场依然是正交 的, 从而使耦合系数 k 为零. 因此从以上分析中可以 得出结论: 在声疏密波产生的超声光栅的扰动下对 称的 L P 01模与非对称的 L P 11模式间并不能发生有 效的耦合.
    Η Β Η ·484·　　　　　　　　　　　　　　　　 　 上 海 大 学 学 报 (自 然 科 学 版) 　　　　　　　　　　　　 　　第 7 卷 1. 3　倾斜光纤超声光栅引起的光波模式的耦合 在垂直的光纤超声光栅中, 由于折射率扰动的 影响在纤芯的径向上为对称的, 所以L P 01模与 L P 11 模之间不会发生有效的耦合. 如果当光栅条纹与光 纤轴有一定的倾斜角 时, 对称的 L P 01模与不对称 模 L P 11模式之间就会发生模式间的耦合[ 26, 27 ]. 这是 由于倾斜光栅条纹导致的折射率扰动在光纤纤芯的 径向是不对称的, 这样就破坏了L P 01、L P 11这两个对 称模与非对称模之间的正交性, 从而使得这两个模 式之间发生有效的耦合. 在倾斜光栅中L P 01、L P 11这 两个模式间的耦合系数 k 可表示为[ 28 ] 光纤轴线有一定角度 的夹角, 如图 4 所示, 其中虚 线所示为光纤纤芯. 倾斜的超声光栅引起光纤纤芯 圆周方向折射率变化的不对称, 破坏了同向的对称 与不对称的两个模式间电场的正交性, 导致这两个 模式间能产生有效的耦合. 通过这种方法, 即使加上 声疏密波, 通过选择超声光栅的倾斜角 至 3°左右, 这样可以使得对称的 L P 01模与非对称的 L P 11模之 间发生耦合强度最大. g) 图 4　倾斜超声光栅的示意图 (15) F ig. 4　D iagram of fiber sub ject to titled u ltrason ic grating g + i 0) 2　光纤超声光栅与光纤光栅的分析 k c = ( 0n n 8)∫2 d 0 ∫a rd r k s = ( 0n n 8)∫2 d 0 ∫a rd r exp (2i E 11c ( r, r co s ) E exp (2i E 11s ( r, r sin ) 0 sin 01 ( r) , 0 sin 01 ( r) , E (16) 其中, k c 表示 L P 01与 L P 11偶模间的耦合系数, k s 表 示 L P 01与 L P 11奇模间的耦合系数, 为倾斜光栅的 g 为倾斜光栅的周期. 从 (15)、(16) 式可以 倾斜角, 看出, 由于光栅有了一定的倾斜角 , 使得原本不能 耦合的 L P 01、L P 11q (q= c 表示偶模, q= s 表示奇模) 两个模式间发生了有效的耦合. 在光纤纤芯半径 a m , 相对折射率为 0. 01, 两模式间的拍差为 = 3. 62 m 的条件下, 根据式 (15)、(16) 可以计算得 225. 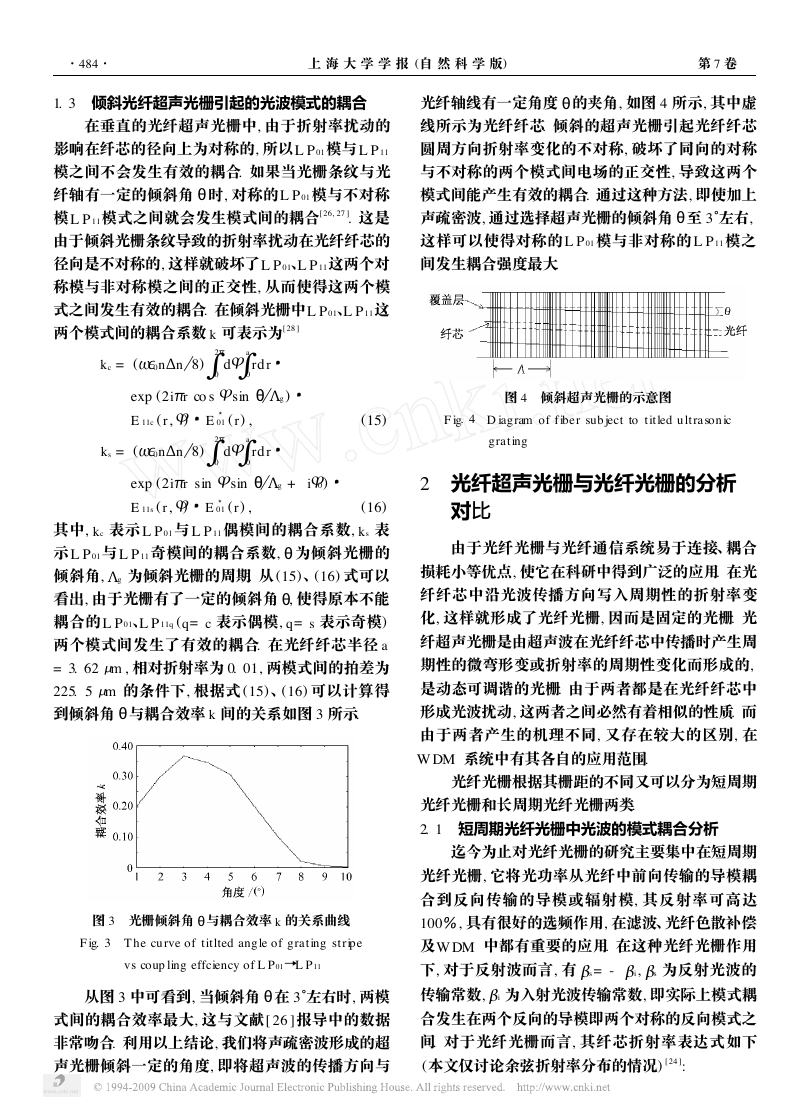5 到倾斜角 与耦合效率 k 间的关系如图 3 所示. 对比 由于光纤光栅与光纤通信系统易于连接、耦合 损耗小等优点, 使它在科研中得到广泛的应用. 在光 纤纤芯中沿光波传播方向写入周期性的折射率变 化, 这样就形成了光纤光栅, 因而是固定的光栅. 光 纤超声光栅是由超声波在光纤纤芯中传播时产生周 期性的微弯形变或折射率的周期性变化而形成的, 是动态可调谐的光栅. 由于两者都是在光纤纤芯中 形成光波扰动, 这两者之间必然有着相似的性质. 而 由于两者产生的机理不同, 又存在较大的区别, 在 W DM 系统中有其各自的应用范围. 光纤光栅根据其栅距的不同又可以分为短周期 光纤光栅和长周期光纤光栅两类. 2. 1　短周期光纤光栅中光波的模式耦合分析 迄今为止对光纤光栅的研究主要集中在短周期 光纤光栅, 它将光功率从光纤中前向传输的导模耦 合到反向传输的导模或辐射模, 其反射率可高达 , 具有很好的选频作用, 在滤波、光纤色散补偿 100 及W DM 中都有重要的应用. 在这种光纤光栅作用 下, 对于反射波而言, 有 s 为反射光波的 传输常数, i 为入射光波传输常数, 即实际上模式耦 合发生在两个反向的导模即两个对称的反向模式之 间. 对于光纤光栅而言, 其纤芯折射率表达式如下 (本文仅讨论余弦折射率分布的情况) [ 24 ]: s= - i, 图 3　光栅倾斜角 与耦合效率 k 的关系曲线 F ig. 3　T he cu rve of titlted angle of grating stripe vs coup ling effciency of L P 01→L P 11 从图 3 中可看到, 当倾斜角 在 3°左右时, 两模 式间的耦合效率最大, 这与文献[ 26 ]报导中的数据 非常吻合. 利用以上结论, 我们将声疏密波形成的超 声光栅倾斜一定的角度, 即将超声波的传播方向与
    2 2 2 2 2 2·584· Λ 第 6 期　　　　　　　　　　　　　　　　肖彦萍, 等: 声光光纤模式耦合的分析 2 n (z ) = n eff + co s 2 z , (17) 为光栅栅距周期. 对于弱光纤光栅, 有 为光栅强度参 式中, neff为光纤芯区的有效折射率, 数, 1, 同样可以采用微扰理论来分析弱光纤光栅, 则由光 纤光栅产生的折射率扰动可表示为 n = n 2 (z ) - n 2 eff = 2n eff co s 2 z . (18) 由公式 (1) 可以计算出在光纤光栅中发生耦合的前 向模 E 0 与反向模 E 1 之间的耦合系数, 由于这两个 耦合的模式是反向的, 因此有 E 1 = E 0 ( r) exp (- j 01z ) , k =∫D (n 2 - n 2 eff) E 0E 1 dA = = nE 0 ( r) exp ( j 01z ) E 0 r exp ( j 01z ) rd rd n exp (2j 01z ) E 2 0 ( r) rd rd . (19) 　　从公式 (17) 中可以看出, 由于光纤光栅引起的 折射率变化是沿其长度方向, 并没有改变耦合模式 电场的正交性, 所以耦合只能发生在两个相互反向 的非正交导模之间, 而对于两个同向的、正交的模式 间是不能发生有效的耦合. 这与前面分析的由声疏 密波产生的超声光栅并不能使得两个L P 01、L P 11模 式间发生有效耦合的结论是一致的. 2. 2　长周期光纤光栅中光波的模式耦合分析 在长周期光纤光栅中, 并不是所有的前向传输 模式间都可以发生耦合, 有效的耦合只能发生在同 向的导模与横向电场分量中心最强的包层模之间, 这样的包层模只能是 H E 1p 模[ 25 ], 即对称的线偏振 模. 也就是说, 只有在两个同向的导模与对称的包层 模之间才能发生模式耦合, 而对于同向的导模与非 对称的包层模之间是不能发生有效耦合的. 2. 3　光纤超声光栅与光纤光栅模式耦合的比较 长周期光纤光栅与短周期光纤光栅的工作机理 是相同的, 只是由于短周期光纤光栅其光栅周期很 小, 大约为零点几个 m , 前向传输的导模只能与后 向导模或包层模耦合; 而长周期光纤光栅因光栅周 期很大, 约为几百个 m , 它可以实现前向传输的导 模与其它前向导模或前向辐射模之间的耦合, 具有 无后向反射的特点, 可以避免由后向反射带来的回 波或杂散激发. 由超声产生的光纤超声光栅的栅距 大约为几十至几百个 m (根据声波频率而变化) , 这样的栅距长度范围与长周期光纤光栅的栅距近 似, 所以光纤超声光栅与长周期光纤光栅有着类似 的性质. 对于短周期光纤光栅, 两个同向的、正交的模式 间是不能发生有效的耦合. 对于长周期光纤光栅, 两 个同向的导模与对称的包层模之间才能发生模式耦 合, 而两个同向的导模与非对称的包层模之间是不 能发生有效耦合的. 由于光纤超声光栅与长周期光 纤光栅在性能上的类似性, 我们可以验证在光纤超 声光栅中并不是所有的前向传输模式间都可以发生 耦合. 这与我们前面分析的由超声疏密波产生的光 纤超声光栅并不能使得对称的L P 01模与非对称的 L P 11模式发生有效的耦合这一结论是符合的. 3　结　　论 通过以上分析对比, 在比较了声切变波和疏密 波激发的超声光栅对双模光纤中L P 01、L P 11模间耦 合的影响后, 可以得到不同性质的扰动对L P 01、L P 11 模式间耦合有不同的影响. 对于光纤声光器件, 在声 切变波的作用下, 对称的L P 01与非对称的 L P 11模式 可以产生有效的耦合. 而在声疏密波的作用下, L P 01、L P 11模式并不能产生有效的耦合, 但是当由声 疏密波激发的超声光栅条纹与纤芯有一定的倾斜角 时, L P 01与L P 11模式间就可以发生有效的耦合. 根据 理论计算得到在倾斜角 为 3°左右时, 可以得到最 大的耦合效率, 并且由此设计出能使得L P 01与 L P 11 模式间转换效率最高的倾斜超声光栅. 由此得到一 个非常重要的结论, 除了超声光栅的周期必须满足 这两个耦合模式间的相位匹配条件外, 它还必须要 破坏这两个模式间径向电场的正交性, 这样两个同 向的、对称模与非对称模之间才能发生有效的耦合. 这一结论为光纤声光器件控制超声光栅产生有效的 模式耦合提供了理论依据. 参考文献: [ 1 ]　B irk s T A , et al. Fou r po rt frequency sh ifter w ith a nu ll taper coup ler [J ]. O p t L ett, 1994, 19 (23) : 1964 - 1966. [ 2 ]　O sn i L isboa, et al. N ew configu ration fo r an op tical op tic frequency sh ifter [J ]. SP IE, F iber fiber acou sto O p tic Sen so rs IV , 1990, 1267: 17- 23. [ 3 ]　 K im B Y, et al. A ll fiber acou sto op tic fresquency sh ifter [J ]. O p t L ett, 1986, 11 (6) : 389- 391. [ 4 ]　R isk W P, K ino G S. A cou sto op tic fiber op tic fre
    ·684·　　　　　　　　　　　　　　　　 　 上 海 大 学 学 报 (自 然 科 学 版) 　　　　　　　　　　　　 　　第 7 卷 quency sh ifter u sing periodic con tact w ith a cop ropa gating su rface acou stic w ave [J ]. O p t L ett, 1986, 11 (5) : 336- 338. [ 5 ]　T u ran E rdogan. F iber grating spectra [J ]. J L igh t w ave T echno l, 1997, 15 (8) : 1277- 1294. [ 6 ]　H ill K O , M eltz G. F iber b ragg grating techno logy J L igh tw ave T ech fundam en tals and overview [J ]. no l, 1997, 15 (8) : 1263- 1276. [ 7 ]　L iu W F , Ph ilip St, R u ssell J , et al. 100% efficien t band acou stoop tic tunab le reflecto r u sing fiber J L igh tw ave T echno l, 1998, 16 narrow b ragg grating [J ]. (11) : 2006- 2009. L ett, 1994, 6 (3) : 390- 393. [ 16 ]　Paek E G, Choe J Y, O h T K. T ran sverse grating op tic tunab le assisted narrow ed filter [J ]. O p t L ett, 1998, 23 (16) : 1322- 1324. bandw idth acou sto [ 17 ]　 Yun S H , et al. A ll fiber tunab le filter and laser m ode fiber [J ]. O p t L ett, 1996, 21 based on tw o (1) : 27- 29. [ 18 ]　傅焰峰, 等. 波导声光可调谐滤光器及其在W DM 网 络 中的应用 [J ]. 压电与声光, 1996, 18 (5) : 311 - 315. [ 19 ]　靳晓民, 等. 声光可调谐滤波器的进展 [J ]. 光通信技 术, 1995, 19 (2) : 116- 120. [ 8 ]　赵玉成, 等. B ragg 光纤光栅 [J ]. 光通信技术, 1995, 19 [ 20 ]　叶培大. 光纤理论 [M ]. 上海: 知识出版社, 1985. 45 (4) : 301- 304. - 63. [ 9 ]　O rtega B , et al. A ll fiber op tical add drop m u ltip lexer based on a selective fu sed coup ler and a single fiber b ragg grating [J ]. A pp l O p t, 1998, 37 (33) : 7712- 7717. [ 10 ]　B aum ann I, et al. Com pact all fiber add drop m u lti IEEE Pho ton p lexer u sing fiber b ragg gratings [J ]. T echno l L ett, 1996, 8 (10) : 1331- 1333. [ 21 ]　B lake J N , et al. A nalysis of in term odal coup ling in a m ode fiber w ith period m icrobends [ J ]. O p t tw o L ett, 1987, 12 (4) : 281- 283. [ 22 ]　T aylo r H en ry F. B ending effects in op tical fibers[J ]. J L igh tw ave T echno l, 1984, L T-2 (5) : 617- 628. [ 23 ]　刘广玉, 等. 新型传感器技术及应用 [M ]. 北京: 北京 航空航天大学出版社, 1995. 209- 211. [ 11 ]　B irk s T A , et al. 2 × 2 single m ode fiber rou ting [ 24 ]　苑立波. 光纤光栅原理与应用 (一) ——光纤光栅原理 sw itch [J ]. O p t L ett, 1996, 21 (10) : 722- 724. [J ]. 光通信技术, 1998, 22 (1) : 70- 78. [ 12 ]　Cu lverhou se D O , et al. A ll fiber 2×2 po larization IEEE Pho ton T echno l L ett, in sen sitive sw itch [J ]. 1997, 9 (4) : 455- 457. [ 13 ]　D avid A Sm ith, et al. Evo lu tion of the acou sto op tic J L igh tw ave T ech w avelength rou ting sw itch [J ]. no l, 1996, 14 (6) : 1005- 1019. [ 14 ]　D avid A Sm ith, et al. M u ltiw avelength perfo rm ance op tic sw itch [J ]. J L igh tw ave of an apodized acou sto T echno l, 1996, 14 (9) : 2044- 2051. [ 15 ]　A lessandro A D , et al. M u ltichannnel operation of rou ting IEEE Pho ton T echno l an sw itch fo r W DM system s [J ]. op tic w avelength in tegrated acou sto [ 25 ]　孔　梅, 等. 长周期光纤光栅导模与包层模的耦合分 析 [J ]. 光学学报, 1999, 19 (3) : 369- 373. [ 26 ]　Guan Yali, et al. A nalysis on design and characteris converter [J ]. SP IE, 1998, 3552: 262- tics of m ode 266. [ 27 ]　 H ill K O , et al. Efficien t m ode conversion in telecomm un ication fiber u sing ex ternally w ritten gratings [J ]. E lectron ics L etters, 1990, 26 (16) : 1270- 1272. [ 28 ]　Kyung Sh ik L ee, et al. T ran sm issive tilted grating IEEE Pho ton L P 11 m ode coup ling [J ]. fo r L P 01 T echno l L ett, 1999, 11 (10) : 1286- 1288. to
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料