第1页 / 共26页
第2页 / 共26页
第3页 / 共26页
第4页 / 共26页
第5页 / 共26页
第6页 / 共26页
第7页 / 共26页
第8页 / 共26页
基于相干信号空间谱测向的Matlab仿真研究.docx
Matlab与通信系统仿真
结课作业
对于M元均匀线阵，阵源间距为d，且假设均为各向同性阵元。阵列远场中在以线阵轴线法线为参考的处有 P
(2-1)
(2-1)式中为快拍数据矢量，是阵元输出信号，。
为阵列阵元噪声矢量，且是与信号源不相关的白噪声，均值为0，方差为，。为输入信号矢量。为
= (2-2)
（ , ）
向量称为第i个信号源的方向向量。矩阵列向量即是阵列方向向量的集合，它表示所有信源的方向，称为阵列
当空间信源互不相干时，对协方差矩阵R进行特征分解，构造信号子空间和噪声子空间，利用其正交性直接采用M
将同时左乘和右乘，可以得到：，所以自相关矩阵的特征值为，前P个特征值为信号特征值, 后M
（2-3）
3.MATLAB仿真
3.1 典型的MUSIC算法
3.1.1 代码如下：
clear all;
clc;
p=2; %入射信号数目
M=4; %阵元个数
fc=1e9; %入射信号中频为1G
DOA=[-20,40]/180*pi; %信号入射DOA
fs=3*fc; %采样频率
N=512; %采样个数
snr=10; %信噪比
T=1/fs; %采样时间间隔
c=3e8; %波速
d=c/fc*0.5; %阵元间距
t=0:T:(N-1)*T; %采样时间区间
s1=sqrt(2)*cos(2*pi*fc*t); %信号数据
s2=sqrt(2)*cos(2*pi*(fc+5e8)*t);
ss=[s1;s2];
s=ss(1:p,:);
%%%%%%%%计算阵列流形矩阵A
A=zeros(M,p);
for k=1:p
for kk=1:M
A(kk,k)=exp(-j*2*pi*fc*(kk-1)*d*sin(DOA(k)
end
end
%%%%%%%%阵列接收数据
y=A*s;
y=awgn(y,snr);
R=y*y'/N;
%%%%%%%%计算噪声子空间
[v,dd]=eig(R);
if(dd(1,1)>dd(2,2))
Un=v(:,p+1:M);
else
Un=v(:,1:(M-p));
end
do=-90:90;
pu=zeros(1,length(do));
kg=1;
for k=-90:90
a=zeros(M,1);
for kk=1:M
a(kk,1)=exp(-j*2*pi*fc*(kk-1)*d*sin(k/180*
end
pu(1,kg)=1/(a'*Un*Un'*a);
kg=kg+1;
end
plot(do,10*log10(abs(pu)),'-r','linewidth',2);
grid on;
title('MUSIC测向');
xlabel('波达方向');
ylabel('MUSIC谱');
disp('MUSIC测向结果:');
for k=1:p
[k1,k2]=max(pu);
DOA_guji(k)=(k2-1)-90;
pu(k2)=0;
end
DOA_guji
3.1.2 MATLAB仿真图：
图6 无相干信号源时的 MUSIC测向
但若存在相干信源时，阵列输出信号协方差的秩 ，对信号协方差矩阵进行特征值分解后，得到的较大的特征值
仿真结果如下：
图7 有相干信号源时的MUSIC测向
因此，我们要对阵列输出的协方差矩阵首先进行预处理，使其阵列协方差矩阵的秩恢复为信号元数P，然后再采用
6.小组成员列表
东北大学秦皇岛分校
计算机与通信工程学院
Matlab 与通信系统仿真
结课作业
班级：
学号：
姓名：
41109
4110932
汪婷静
指导教师： 刘福来
目录
1．阵列天线处理相关信号……………………………………………………………………….3
1.1 引言 ……………………………………………………………………………………...3
1.2 典型的 Music 算法………………………………………………………………………...3
1.2.1 窄带阵列相干源的数学模型……………………………………………………..3
1.3 处理相关信号的算法……………………………………………………………………...5
1.3.1 前向空间平滑算法………………………………………………………….........5
1.3.2 前后向空间平滑算法……………………………………………………………..6
1.3.3 修正 MUSIC(MMUSIC) ………………………………………………………….7
2.前后向平滑算法和改进型 Music 的性能比较………………………………………………….8
2.1 去相关能力分析……………………………………………………………………..8
2.2 均方值误差分析……………………………………………………………………..9
2.2.1 Music 算法测向均方根误差分析…………………………………………………9
2.4.2mmusic 算法和前后向平滑算法的均方根的比较……………………………….9
3．MATLAB 仿真…………………………………………………………………………………10
3.1 典型的 MUSIC 算法……………………………………………………………………..10
3.1.1 代码如下…………………………………………………………………………11
3.1.2 MATLAB 仿真图………………………………………………………………....12
3.2 平滑空间算法的仿真…………………………………………………………………….13
3.2.1 代码如下…………………………………………………………………………13
3.2.2 MATLAB 仿真图…………………………………………………………………15
3.3 MMUSIC 算法的仿真…………………………………………………………………….16
3.3.1 代码如下…………………………………………………………..……………..16
3.3.2MATLAB 仿真图………………………………………………………………….18
3.4 去相关仿真……………………………………………………………………………….18
3.4.1 代码如下…………………………………………………………………………18
3.5 均方值误差仿真………………………………………………………………………….21
3.5.1Music 算法侧向均方根误差分析代码…………………………………………...21
3.6mmusic 算法和前后向平滑算法的均方根比较代码…………………………………….22
4.小结……………………………………………………………………………………………..25
5.参考文献………………………………………………………………………………………..26
6、小组成员列表…………………………………………………………………………………26
2
基于相干信号空间谱测向的 Matlab 仿真研究
1.阵列天线处理相关信号
1.1 引言
由于多径传播、电磁干扰等因素的影响，相干信源存在的电磁环境是经常碰到
的。当空间存在相干源时，经典的超分辨 DOA 估计方法：MUSIC 算法和 ESPRIT
算法，已经失去了其高分辨性能优势，有时甚至不能正确地估计出信源的真实方
位。新 MUSIC 算法在空间不存在相干源时，其估计性能基本上是和 MUSIC 算
法是接近的，但若有相干源存在时，其估计性能也是大大降低。因此，若将其用
于相干源，必须和经典的 MUSIC 算法一样，首先对阵列输出的协方差矩阵进行
各种去相干处理，再采用新 MUSIC 算法实现对相干信源的 DOA 估计。通过研
究与发现我们总结出了两种去相关算法：前/后向空间平滑(Forward/Backward
Spatial Smoothing Technique)和修正 MUSIC(MMUSIC)[1]。这两种方法各自有其
优缺点，笔者系统地描述了它们的基本去相关原理，并对其重要性能指标作了计
算机仿真和比较，对算法选择具有一定的参考价值。
1.2 典型的MUSIC算法
1.2.1 窄带阵列相干源的数学模型
对于M元均匀线阵，阵源间距为d，且假设均为各向同性阵元。阵列远场中
在以线阵轴线法线为参考的 (
kθ
k
1,2,... )
P
处有 P 个窄带点源以平面波入射，以
阵列第一阵元为参考点，某一特定信号到达线阵时，各阵元接收信号间仅仅存在
因波程差引起的相位差。阵列接收的快拍数据可由下式表示为:
X( )= A(
t
)S( )+ N( )
t
t
(2-1)
(2-1)式中 ( )tX 为 M 1 快拍数据矢量，是阵元输出信号，
X
( )
t
[
x t
1
( ),......
x
M
( )]T
t
。
( )tN 为 M 1 阵列阵元噪声矢量，且是与信号源不相关的白噪声，均值为0，方
3
差为 2
n ，
N
( )
t
[
n t
1
( ),......
n
M
( )]T
t
。 ( )tS 为输入信号矢量
S
( )
t
[
s t
1
( ),......
s
M
( )]T
t
。
( )A 为阵列的流形矩阵,如式(2-2)所示。
( )
A
[ (
a
1
),...... (
a
)]P
=
e
)
(
1
j
1
...
e
)
(
1
j
2
...
(
j M
e
1)
1
(
)
(
j M
e
1)
2
(
...
...
...
)
e
)
1
(
j
p
...
(
j M
e
1)
p
(
)
(2-2)
（
i
(
)
d
i
sin(
2
)ia 称为第i个信号源的方向向量。矩阵 A 列向量即是阵列方向向量的
向量 (
1,2,...
M
）
)
i
,
集合，它表示所有信源的方向，称为阵列的方向矩阵。阵列的协方差矩阵R定义
为
R
E
[
X X
( )
t
H
( )]
t
AR A
S
H
2
I ,式中
SR
[
E
S
( )
t
S
H
( )]
t
为信源的协方差矩
阵[2]。
当空间信源互不相干时，对协方差矩阵R进行特征分解，构造信号子空间和
噪声子空间，利用其正交性直接采用MUSIC或ESPRIT算法进行DOA 估计，令
其特征值分解为
sR U U ,式中，
H
2
1(
diag
,......,
2
)M
，如果信号不相干，
则A 为列满秩，
rank
(
SAR A
PH
)
，于是
将 R 同时左乘
HU 和右乘U ，可以得到：
H
U AR A U
H
S
2
diag
P
1(
,...,
2
,0,...0)
，
H
U RU = U AR A U
H
H
S
2
U U =
H
diag
2
2
1(
P
,...,
,0,...0)
2
I ，所以自相关矩阵 R
的特征值为 2
1
2
,...
,...
2
P
,
2
2
2
，前P个特征值为信号特征值, 后M-P个特征
值为噪声特征值, 由信号特征值对应的所有特征向量形成的矢量空间称为信号
子空间, 信号子空间同时可以用信号的方向矢量 (
)ia
表示。由噪声特征值对应
的特征向量形成的矢量空间称为噪声子空间, 二者组成信号自相关矩阵的信息
空间,利用信号矢量与噪声空间的所有矢量都是正交的这一特性来估计来波信号
的到达角（如式2-3所示）, 即MUSIC法。
4
=
P
（ ）
1
H
UU a
H
（ ）a
( )
（2-3）
1.3 处理相关信号的算法
1.3.1 前向空间平滑算法
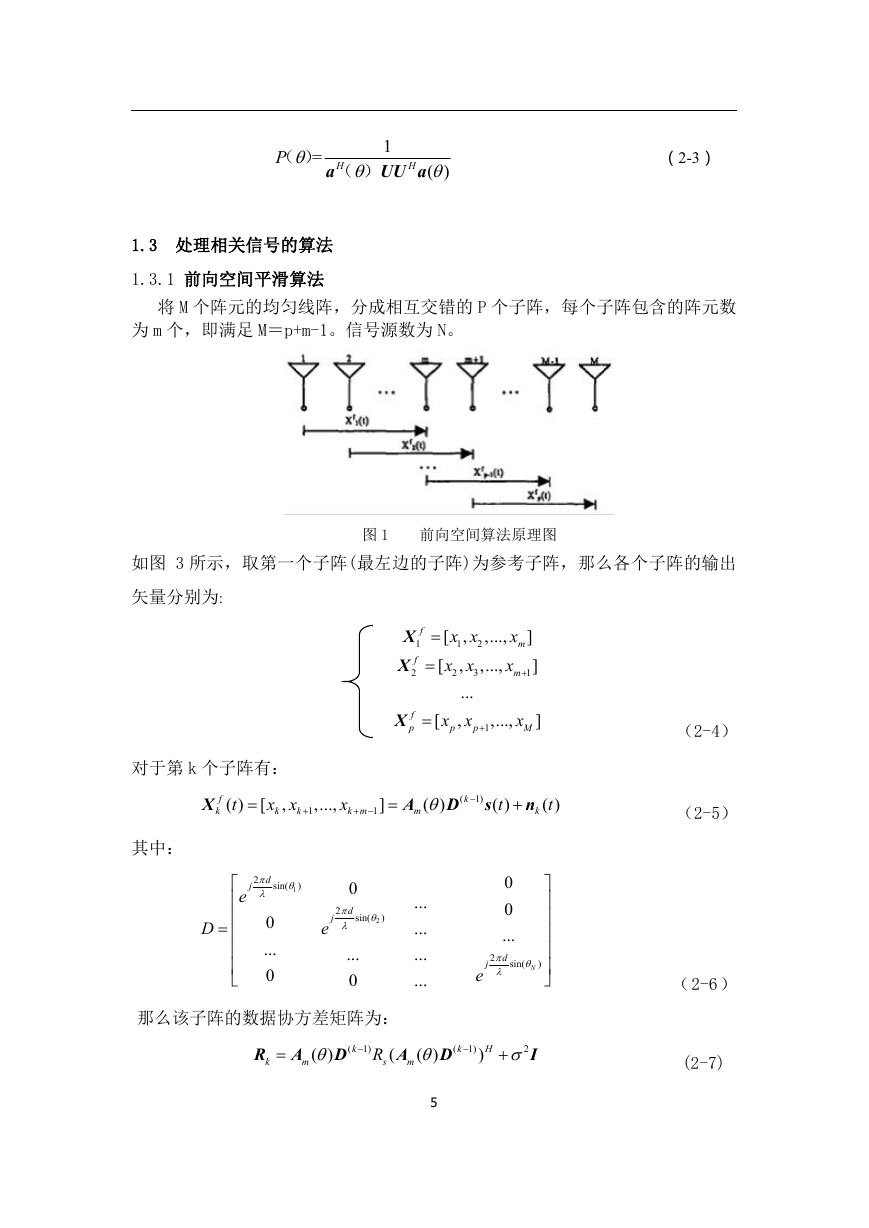
将 M 个阵元的均匀线阵，分成相互交错的 P 个子阵，每个子阵包含的阵元数
为 m 个，即满足 M＝p+m-1。信号源数为 N。
如图 3 所示，取第一个子阵(最左边的子阵)为参考子阵，那么各个子阵的输出
图 1
前向空间算法原理图
矢量分别为:
m
]
]
m
1
x
M
]
f
X
1
f
X
2
,...,
,
[
x
x x
1
2
,
[
,...,
x
x x
2
3
...
,
x
,...,
x
[
p
1
p
1)
( )
k
D
(
s
( )
t
n
k
( )
t
X
f
p
对于第 k 个子阵有：
X
f
k
( )
t
[
,
x x
k
k
,...,
x
1
k m
]
A
m
1
其中：
D
je
sin(
1
2
d
0
...
0
)
je
)
2
0
2
d
sin(
...
0
...
...
...
...
0
0
...
2
d
sin(
N
)
je
那么该子阵的数据协方差矩阵为：
R
k
A
m
( )
D
(
k
1)
R
s
(
A
m
( )
D
(
k
1)
H
)
2
I
5
（2-4）
（2-5）
（ 2-6 ）
(2-7)
其中， mA 是一个 m×p 的参考子阵(通常取第一个子阵)的导向矢量矩阵，
A
m
( )
[
a
m
(
1
),......
a
m
sR 为信号的协方差矩阵，
R
s
)]
H
(
N
E ss
a
m
(
k
)
[1,
e
j
2
d
sin(
k
)
,....,
e
j
2
d
sin(
k
)
T
]
，
。
，
前向空间平滑技术是通过求各个子阵协方差矩阵的均值来实现的，即取前向平滑
修正的协方差矩阵为:
f
R
k
R
1 p
kp
1
（2-8）
可以证明，当满足 m>N, p>N 时，前向空间平滑数据协方差矩阵 fR 是满秩的。即
可以通过特征分解求得相应的信号子空间和噪声子空间。
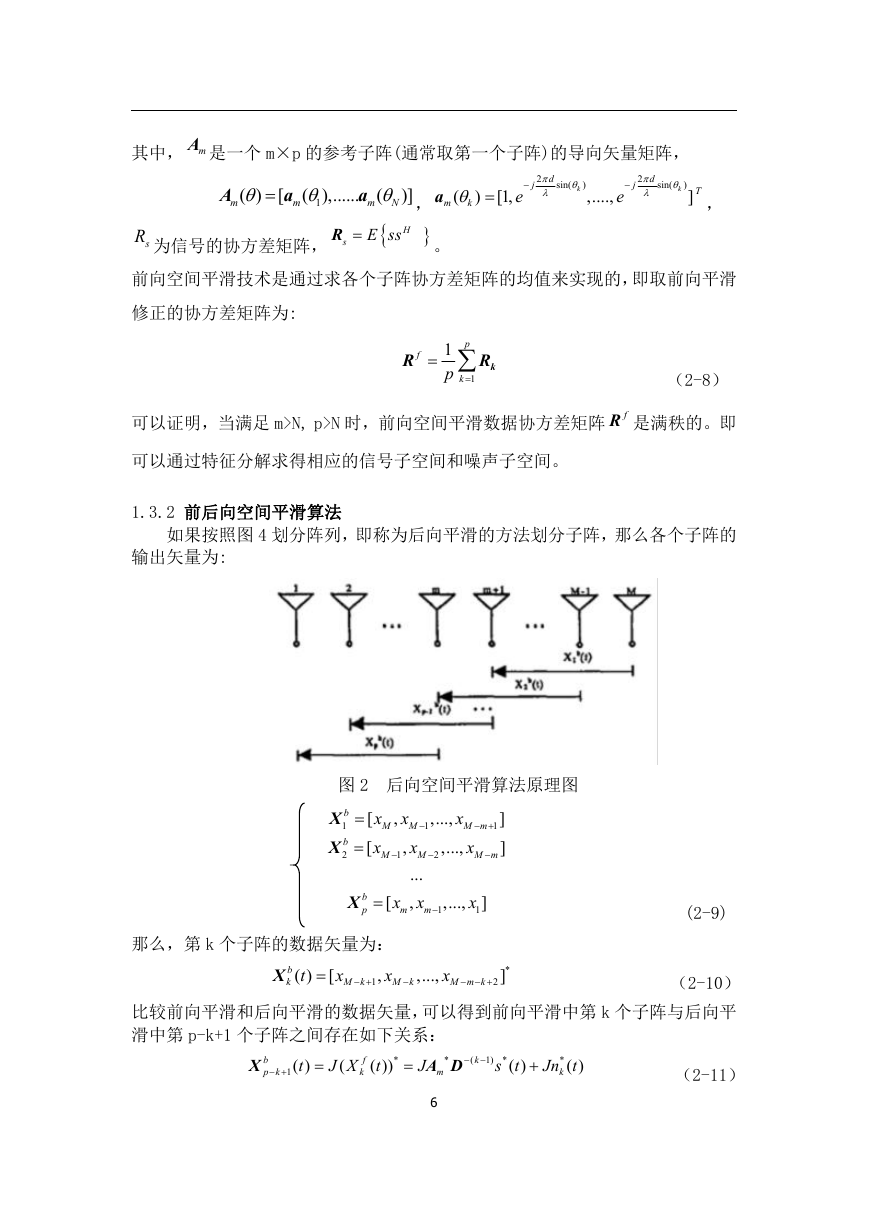
1.3.2 前后向空间平滑算法
如果按照图 4 划分阵列，即称为后向平滑的方法划分子阵，那么各个子阵的
输出矢量为:
图 2 后向空间平滑算法原理图
X
X
b
1
b
2
[
[
x
x
,
M
M
1
x
,
,...,
x
,...,
2
]
]
1
M m
x
M m
X
b
p
[
x
m
,...,
x
1
]
1
1
M
x
M
...
,
x
m
那么，第 k 个子阵的数据矢量为：
x
( )
t
X
x
[
,
M k
1
b
k
M k
,...,
x
M m k
2
*
]
(2-9)
（2-10）
比较前向平滑和后向平滑的数据矢量，可以得到前向平滑中第 k 个子阵与后向平
滑中第 p-k+1 个子阵之间存在如下关系：
X
b
p k
1( )
t
(
J X t
( ))
f
k
*
J
*
A D
m
(
k
1) *
( )
s t
( )
Jn t
*
k
（2-11）
6
J
0
0
...
1
0
...
...
0
...
1
...
0
1
0
...
0
，所以后向平滑第 p-k+1 个子阵的数
(2-12)
(2-13)
其中 J 为 m 的交换矩阵。
据协方差矩阵为:
R
b
p k
1
JA D
*
m
(
k
1)
*
R D
(
s
(
k
1)
H
)
(
H
A J
m
*
)
2
I
那么后向空间平滑修正的数据矩阵为:
b
R
1 p
kp
1
R
b
1
p k
取前向平滑和后向平滑数据协方差矩阵的平均，即前后向空间平滑的数据矩阵，
即
fb
R
f
b
R R
2
(2-14)
同样可以证明，当满足 m>N, p>N 时，后向空间平滑数据协方差矩阵 bR 是满秩的。
1.3.3 修正 MUSIC(MMUSIC)
在前/后向空间平滑技术中，如果取子阵阵元数等于总的阵元数的特殊情况
下，就是修正 MUSIC(MMUSIC)算法。其基本原理如下:在 MUSIC 算法中接收数据:
X( )= A(
t
)S( )+ N( )
t
t
(2-15)
阵列的协方差矩阵 R 定义为
R
E
[
X X
( )
t
H
( )]
t
AR A
S
H
2
SR
[
E
S
( )
t
S
H
( )]
t
为信源的协方差矩阵。令
)(
tY
JX
* t
)(
,其中
I ,式中
)(* tX 是 X(t)的复共
轭，J 为 M*M 阶的交换矩阵，它将向量 X(t)向量倒排，定义为：
J
0
0
...
1
0
...
...
0
...
1
...
0
1
0
...
0
，
显然 J2=I，Y(t)的协方差为 Ry=E[Y(t)*YH(t)]=JA*RS(A*)HJ+σ2I=JR*J,所以总的
协方差矩阵为 R1=(R+Ry)/2,所得 R1 为满秩。
7
2.前后向平滑算法和改进型Music的性能比较
2.1去相关能力分析
空间平滑和MMUSIC算法都是通过改善协方差矩阵特征值的分布来去相关的，
这样有助于减小DOA估计的方差，因为DOA 估计的方差与特征值
的关系为：
[(
i
i
2
])
E
其中
d
(
2
2
N
)
i
[
P
m
1
m
2
)
(
(
da
H
a
)
(
V
m
i
2
2
/[]
d
H
)
(
V
m
i
2
]
/)
i
d
i
，Vm为R1的特征向量
可以看出，信号子空间特征向量对应的特征值 λm(m=1, 2, …, P)愈接近噪声方差
σ2，则DOA估计方差愈大，反之DOA估计方差愈小计算机仿真表明，前/后向空
间平滑方法比MMUSIC方法的信号子空间特征向量对应的特征值λm(m=1, 2, …,
P)愈接近噪声方差σ2，去相关性能降低。
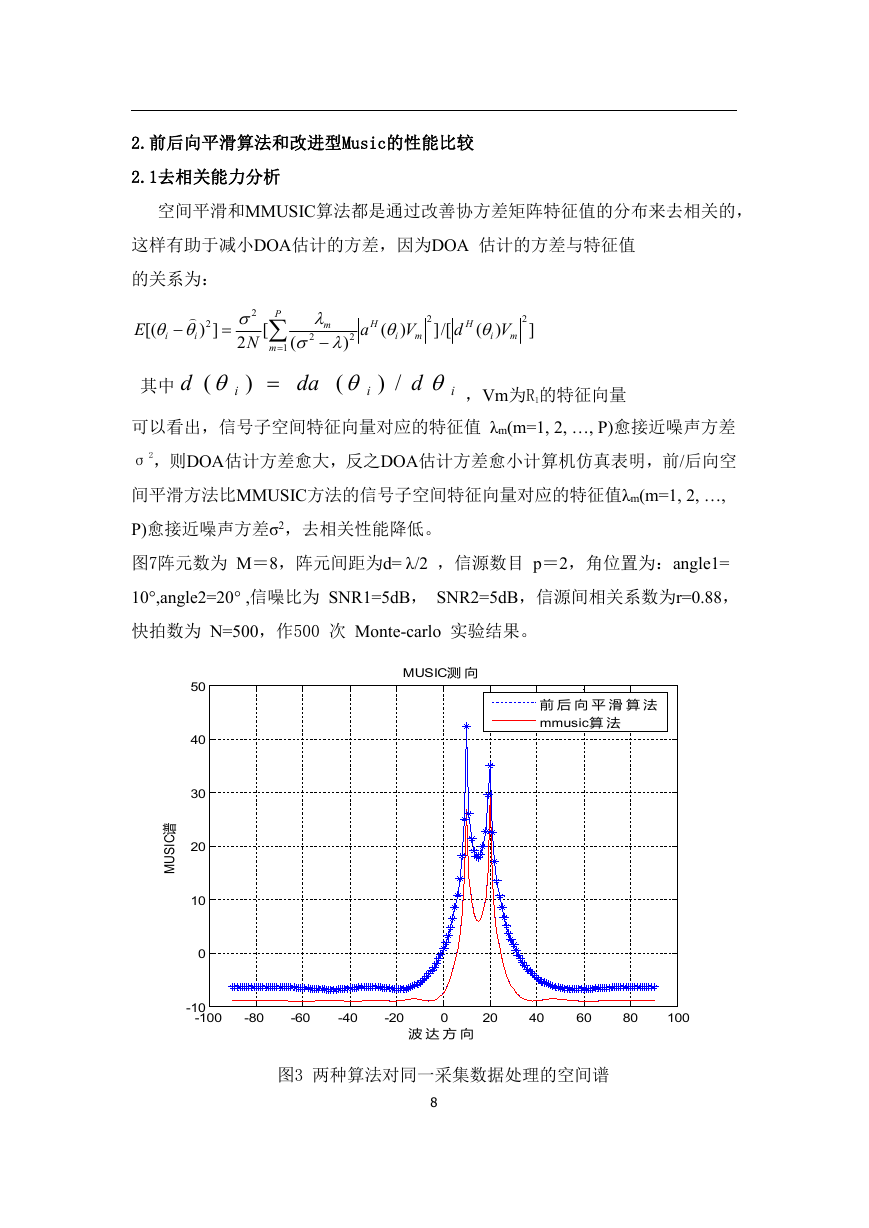
图7阵元数为 M＝8，阵元间距为d= λ/2 ，信源数目 p＝2，角位置为：angle1=
10°,angle2=20° ,信噪比为 SNR1=5dB， SNR2=5dB，信源间相关系数为r=0.88，
快拍数为 N=500，作500 次 Monte-carlo 实验结果。
MUSIC测 向
前 后 向 平 滑 算 法
mmusic算 法
50
40
30
20
10
0
I
谱
C
S
U
M
-10
-100
-80
-60
-40
-20
0
波 达 方 向
20
40
60
80
100
图3 两种算法对同一采集数据处理的空间谱
8
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
