鲁棒主成分分析算法综述.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.80M 资料格式：pdf 举报版权申诉

weixin_38606076-12131824-16359647671526055723.pdf-第1页.png

第1页 / 共12页

weixin_38606076-12131824-16359647671526055723.pdf-第2页.png

第2页 / 共12页

weixin_38606076-12131824-16359647671526055723.pdf-第3页.png

第3页 / 共12页

weixin_38606076-12131824-16359647671526055723.pdf-第4页.png

第4页 / 共12页

weixin_38606076-12131824-16359647671526055723.pdf-第5页.png

第5页 / 共12页

weixin_38606076-12131824-16359647671526055723.pdf-第6页.png

第6页 / 共12页

weixin_38606076-12131824-16359647671526055723.pdf-第7页.png

第7页 / 共12页

weixin_38606076-12131824-16359647671526055723.pdf-第8页.png

第8页 / 共12页

文本预览

中国科技论文在线 http://www.paper.edu.cn 鲁棒主成分分析算法综述肖萌，温罗生 ** （重庆大学数学与统计学院，重庆 401331 ）摘要：主成分分析（principle component analysis）是对高维数据进行处理、分析、压缩以及可视化的一个流行工具。在网页查询、计算机视觉中的生物信息应用、图像分析等方面有广泛的应用。但是在现实场景中的应用和表现往往会受外点和受损的观察数据等的影响，使其表现不尽如人意。因此增强主成分分析的鲁棒性就显得尤为重要.John Wright 等人提出的鲁棒主成分分析模型是目前最流行的模型.本文针对 John Wright 等人提出的鲁棒主成分分析模型，总结了近年来比较实用的几个算法。通过模拟实验对这些算法的运行效果和效率进行了对比。并在最后给出了鲁棒主成分分析在背景分离方面的一个应用。关键词：鲁棒主成分分析;迭代阈值算法;加速近端梯度法;增广拉格朗日算法中图分类号：TP391 survey on algorithms of robust principal component analysis XIAO Meng , WEN Luosheng collage of mathematics and statistics，Chongqing University 401331 Abstract: Principal Component Analysis (PCA) is a popular tool for high-dimensional data processing, analysis,compression,and visualization. And it has wide applications in web search, bioinformatics, image analysis and so on. However, this model usually breaks down in the real applications because of the outliers and missing data. So it is important to enhance the robust of the PCA model. To achieve this, John Wright etc. proposed the robust principal component analysis model, which is the most popular model at present. This paper makes a brief survey on the existing algorithms of robust principal component analysis and compares the results and running speed with each other by numerical tests. At last, we also give an application about RPCA in background subtraction. Key words: Robust Principal Component Analysis;the Iterative Thresholding Approach; the Accelerated Proximal Gradient Approach;the Methods of Augmented Lagrange Multipliers; 0 引言 5 10 15 20 25 30 由于科学技术的进步和数据采集技术的发展，人类已经进入到大数据时代。海量的数据 35 带给我们丰富的信息，同时也夹杂着很多的噪声有时会影响我们的判断。如何从受污染的海量数据中进行知识的挖掘成为人们越来越关心的问题。主成分分析模型是早期比较流行且成熟的数据分析方法之一，该方法假设对于给定的高维数据位于一个低维的线性子空间中，可以有效的找出数据中最“主要”的元素和结构，去除噪声和冗余，将原有的复杂数据降维，揭示隐藏在复杂数据背后的简单结构。在很大程度上 PCA 的主要目标是有效并且精确的估计 40 这个低维空间。主成分分析是一种统计方法，在网页查询、计算机视觉中的生物信息应用、图像分析等方面有广泛的应用[1-4]。但是缺乏鲁棒性，对噪声很敏感使得该模型和算法已经无法适应当前的需求。因此，当加性噪声矩阵的某些值变化很大时，如何准确有效的从受污作者简介：肖萌（1990-），女，硕士，计算优化通信联系人：温罗生(1975-),男,教授,计算优化负责网络. E-mail: wenluosheng@yahoo.cn - 1 -

中国科技论文在线 http://www.paper.edu.cn 染的矩阵中恢复出低秩矩阵是非常有价值的研究课题。为了实现主成分分析的鲁棒性很多论文提出了各种方法，例如：多元微调、交替最小化 45 和随机采样技术等。但是这些算法的时间效率都不是多项式级的[5-6]。目前应用最广且效率最高的算法是 John Wright 等人提出的鲁棒主成分分析[7-9]。该算法的主要目的是从高度损坏的矩阵中恢复低秩矩阵，其中是个随机的噪声项。本文主要针对 John Wright 等人提出的鲁棒主成分分析模型，总结了近年来比较实用的几个算法。通过数值实验对比了这些算法在运行结果以及运行速率上的优缺点。并在最后给 50 出了鲁棒主成分分析在背景分离方面的一个应用。 1 鲁棒主成分分析模型假设给定的数据按列向量存储在一个大的矩阵中。经典 PCA 研究的问题是找到一个低秩矩阵，使得和之间的差异最小。于是得到下面的有约束的优化模型： (1) 55 其中为所求子空间的目标维数。选取 F 范数相当于假设数据受到了独立同分布的高斯噪声污染。该问题的求解方法是：先求出的奇异值分解（ singular value decomposition），然后将的列向量投影到由的前个左奇异向量张成的子空间中[10]。经典的 PCA 假设数据的噪声是高斯的。但是对于大的噪声或者严重的离群点，PCA 会被它影响，而无法正常工作。实际上，尽管矩阵中只有一个元素发生改变，由经典的 PCA 60 方法得到的估计矩阵也会与真实值相差甚远。而鲁棒 PCA[7,11,17]（robust PCA）的提出改善了经典 PCA 的这一缺陷。鲁棒主成分分析（RPCA）考虑的是这样一个问题：一般我们的数据矩阵会包含结构信息，也包含噪声。那么我们可以将这个矩阵分解成两个矩阵相加，一个是低秩的（由于内部有一定的结构信息，造成各行或者各列是线性相关的），另一个是稀疏的（由于含有噪声， 65 而噪声的稀疏的）。该问题相对应的优化问题模型为： (2) 2 模型求解算法将优化问题(2)当成一个一般的凸优化问题，可以将其重写成一个半定规划问题，通过现有的内点法进行求解[12]。尽管内点法仅需要极少迭代次数就可以收敛，但是在处理高维 70 矩阵的存在困难。假设矩阵的维数是 m，则计算迭代方向的计算复杂度为。因此，在传统的 PC 上用内点法所能求解的矩阵尾数最大不超过。但是在图像或者视频处理过程中，矩阵的维数经常为或者，而网页搜索或者生物医学等方面的应用中涉及到的矩阵维数很有可能达到或者超过。所以内点法在实际的应用中往往不可行。因此出现了一些不受维数制约的有效算法。 - 2 - DAEAEmnDRAAD,min(),FAEEsubjecttorankArDAEmin(,)rmnDDDrD*1,minAEAEsubjecttoDAE6()m210410510610

中国科技论文在线 http://www.paper.edu.cn 75 2.1 迭代阈值算法（the Iterative Thresholding approach）将优化问题(2)正则化，得到： (3) 其中是一个大的正数，因此目标函数仅发生了微小的扰动。通过引入一个拉格朗日乘子可以得到(3)的拉格朗日函数： 80 (4) IT 方法迭代更新，， : (5) (6) 85 其中是一个步长因子，用来加速收敛的。在介绍(5)式和(6)式的精确解之前先引入一个软阈值算子（收缩算子）： (7) 其中并且。这个算子可以扩展到向量或者矩阵。借助于这个算子有如下结论 [12,13]： 90 ，其中为的 SVD 分解。因此得到 IT 算法[7-9]流程如下。 IT 算法的形式简单且收敛，但它的收敛速度比较慢，且难以选取合适的步长。因此 IT 算法具有有限的应用范围。算法 1 迭代阈值算法 input：观察矩阵 , 参数和 While not converge do 1: 2: 3: 4: End while , - 3 - 22*1,11min22FFAEAEAEsubjecttoDAEY22*1111(,,),22FFLAEYAEAEYDAEADY21*11argmin(,,)argmin2kkkkAAFYALAEYAA21111argmin(,,)argmin2kkkkEEFYELAEYEE111()kkkkkYYDAEk[]0xifxSxxifxotherwisexR02*1[]argmin2TFXUSSVXXW211[]argmin2FXSWXXWTUSVWmnDR1(,,)()kUVsvdY[]TkAUVS1()kkEYS1()kkkkkYYDAE

中国科技论文在线 http://www.paper.edu.cn 95 2.2 加速近端梯度算法（the Accelerated Proximal Gradient approach）鲁棒主成分分析问题(2)是以下无约束凸优化问题的一种特殊情况： (8) 其中为赋予内积和范数的 Hilbert 空间，g 和 f 都是凸函数，且 f 为 Lipschitz 连续的。对于这类问题可以用加速近端梯度法来求解。由于是 Lipschitz 连续的故可以用一个二 100 次函数局部逼近。由此可以得到目标函数在处的局部二次逼近： (9) 其中为 Lipschitz 常数。的更新过程为： (10) 该迭代过程的收敛性紧紧依赖于局部逼近点的选择。最自然地选择是令，这可以 105 解释为是一种梯度算法。可以证明令，序列满足，可以提高收敛速率。将我们所得到的优化问题（2）的等式约束松弛到目标函数中，得到如下的拉格朗日函数： (11) 110 令，，，这样我们便可以使用加速近端梯度算法[15]。为了提高收敛速率，可以在迭代过程中变化，从一个较大的初值开始，在每一次迭代中采用几何级数下降直到达到下界。具体算法流程为：算法 2 加速近端梯度法 input：观察矩阵 , 参数 , , , Initialize： , While not converge do 1: 2: 3: 4: 5: 6: , , , , - 4 - min()()()HXFXgXfXH()fXkY2(,)()(),()2fkkkkkLQXYfYfYXYXYgXfLX1argmin(,)HkkXXQXYkYkkYX111()kkkkkktYXXXtkt22+11kkkttt2*11(,,)FLAEAEDAE(,)XAE21()FfXDAE*1()gXAE0mnDR010AA010EE011tt01111()AkkkkkktYAAAt111()EkkkkkktYEEEt1()2AAAEkkkkGYYYD(,,)()AkUVsvdG12[]kTkAUVS1()2EEAEkkkkGYYYD12()kEkkEGS211412kktt1max(,)kk1kk

中国科技论文在线 http://www.paper.edu.cn End while 115 2.3 增广拉格朗日乘子法（the Methods of Augmented Lagrange Multipliers）对于问题(2)构造增广拉格朗日函数如下： (12) 使用精确拉格朗日乘子法（exact ALM）交替迭代矩阵和，直到满足终止条件为止。 120 (13) (14) 记、分别收敛于、，则矩阵的更新公式为： (15) 最后更新参数： (16) 125 其中为常数，为比较小的正数。精确拉格朗日乘子法算法[16]流程如下： Algorithm 3 精确增广拉格朗日乘子法 Input: 观测矩阵 , 参数 Initialize: ; ; While not converge do 1: , , While not converge do 2: 3: 4: end while 5: 6: 更新至 7： End while , - 5 - 2*1(,,,),2FLAEYAEYDAEDAEAE21111*argmin(,,,)argmin()2jjjkkkkkkkAAkFYALAEYAADE21111111argmin(,,,)argmin()2jjjkkkkkkkEEkFYELAEYEEDA11jkA11jkE*1kA*1kEY11**1()kkkkkYYDAE**11ifkkkkFFkkEEDotherwise10mnDR00Y00101kkAA01kkEE0j1(,,)()jkkkUVsvdDEY111()kjTkAUSV111111()kjjkkkkESDAY1jj1*11()kkkkkYYDAEk1k1kk

中国科技论文在线 http://www.paper.edu.cn 可以证明如果参数呈几何增长，那么该方法是阶线性收敛的。如果增长的越快， 130 则收敛速度越快。在该算法的计算过程中主要的计算工作量来自与 SVD 分解，因此选择时应尽量保证 SVD 分解的总次数最少。然而受到交替方向乘子法的启发，并不需要求的精确解，因此可以采用不精确的增广拉格朗日求解。则矩阵和的迭代更新公式为： (17) (18) 135 因此得到不精确拉格朗日乘子法算法[16-17]流程如下： Algorithm 4 非精确的增广拉格朗日乘子法 Input: 观测矩阵 , 参数 Initialize: ; ; While not converge do , 1: 2: 3: 4: 更新至 5: End while 3 数值实验 140 这一部分的实验主要分为两种类型：一是模拟实验，利用 matlab 图像处理工具箱的图像试验本文中提到的方法；二是真实数据，将本文中的算法应用到真实的视频中，用来进行视频背景提取。由于迭代阈值算法收敛速度很慢，耗费时间很久，所以这一部分的实验中我们只选择 2.2 和 2.3 中提到的 3 种算法。实验平台为 Matlab R2010a，在 ADM Athlon(tm)Ⅱ CPU 2.70 GHz，2GB 内存的计算机上完成。 145 3.1 模拟实验选取 matlab 图像处理工具箱中的 5 幅图像“blobs”、“circles”、“phantom”、“text”和“rice”。用 matlab 中 imread 命令分别读取每一幅图像，作为观测数据的稀疏项 E。然后利用 matlab 命令构造一个低秩(秩为 r)矩阵 A=randn(m,r)*randn(r,n)。令 D=A+E 作为我们的观测数据。利用上面的算法恢复出 A 和 E。在这一实验中我们取 r=4, ,误差精度为 1e-3。 - 6 - kQkk,min(,,,)kkAELAEYAE2111*argmin(,,,)argmin()2kkkkkkkAAkFYALAEYAADE21111argmin(,,,)argmin()2kkkkkkkEEkFYELAEYEEDAmnDR000YE0011(,,)()kkkUVsvdDEY11()kTkAUSV1111()kkkkkESDAY111()kkkkkYYDAEk1k1kk0.5m

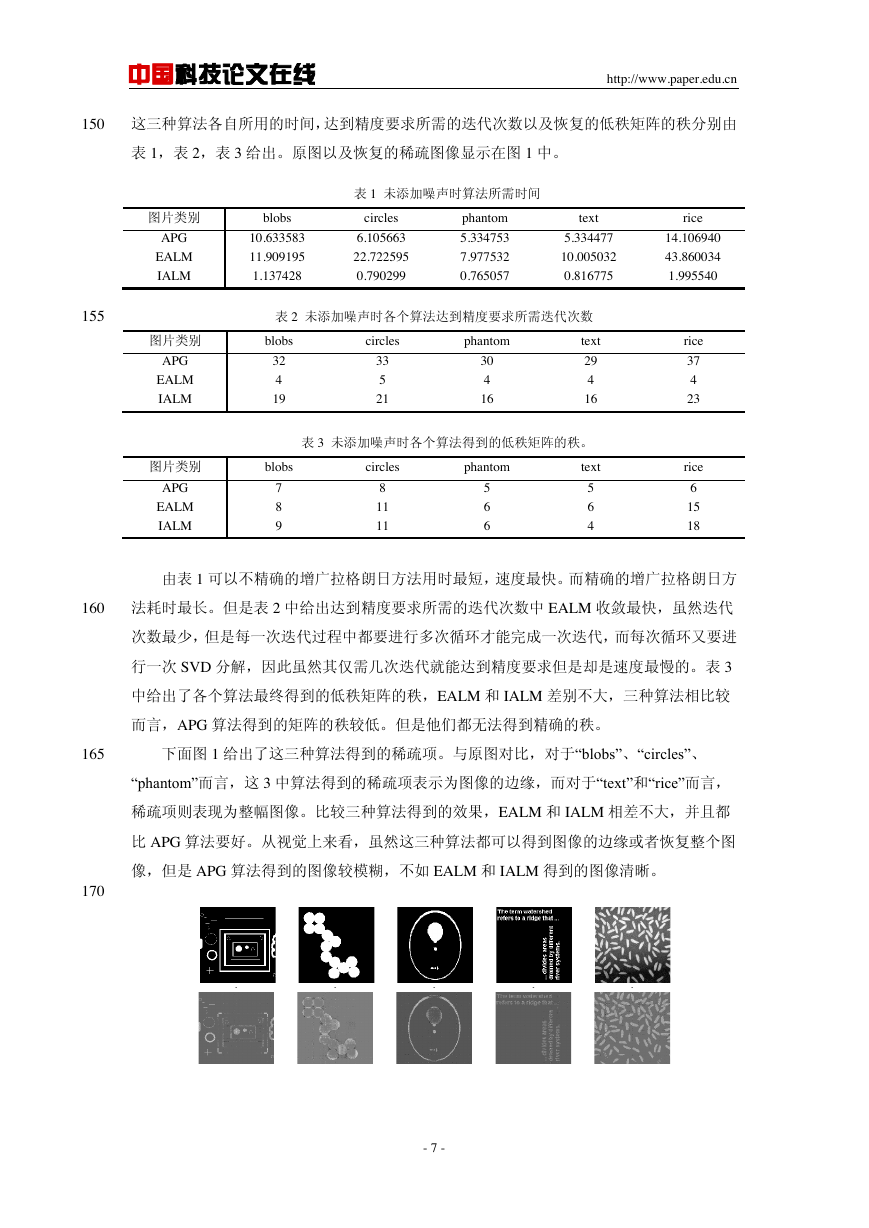
中国科技论文在线 http://www.paper.edu.cn 150 这三种算法各自所用的时间，达到精度要求所需的迭代次数以及恢复的低秩矩阵的秩分别由表 1，表 2，表 3 给出。原图以及恢复的稀疏图像显示在图 1 中。图片类别 APG EALM IALM 表 1 未添加噪声时算法所需时间 blobs circles phantom text 10.633583 11.909195 1.137428 6.105663 22.722595 0.790299 5.334753 7.977532 0.765057 5.334477 10.005032 0.816775 rice 14.106940 43.860034 1.995540 155 表 2 未添加噪声时各个算法达到精度要求所需迭代次数图片类别 APG EALM IALM 图片类别 APG EALM IALM blobs circles phantom text rice 32 4 19 33 5 21 30 4 16 29 4 16 37 4 23 表 3 未添加噪声时各个算法得到的低秩矩阵的秩。 blobs circles phantom text rice 7 8 9 8 11 11 5 6 6 5 6 4 6 15 18 由表 1 可以不精确的增广拉格朗日方法用时最短，速度最快。而精确的增广拉格朗日方 160 法耗时最长。但是表 2 中给出达到精度要求所需的迭代次数中 EALM 收敛最快，虽然迭代次数最少，但是每一次迭代过程中都要进行多次循环才能完成一次迭代，而每次循环又要进行一次 SVD 分解，因此虽然其仅需几次迭代就能达到精度要求但是却是速度最慢的。表 3 中给出了各个算法最终得到的低秩矩阵的秩，EALM 和 IALM 差别不大，三种算法相比较而言，APG 算法得到的矩阵的秩较低。但是他们都无法得到精确的秩。 165 下面图 1 给出了这三种算法得到的稀疏项。与原图对比，对于“blobs”、“circles”、 “phantom”而言，这 3 中算法得到的稀疏项表示为图像的边缘，而对于“text”和“rice”而言，稀疏项则表现为整幅图像。比较三种算法得到的效果，EALM 和 IALM 相差不大，并且都比 APG 算法要好。从视觉上来看，虽然这三种算法都可以得到图像的边缘或者恢复整个图像，但是 APG 算法得到的图像较模糊，不如 EALM 和 IALM 得到的图像清晰。 170 - 7 - Density: 0.09Rel-Err: 6.51e-002Density: 0.17Rel-Err: 6.68e-002Density: 0.08Rel-Err: 7.30e-002Density: 0.10Rel-Err: 7.72e-002Density: 0.38Rel-Err: 5.43e-002

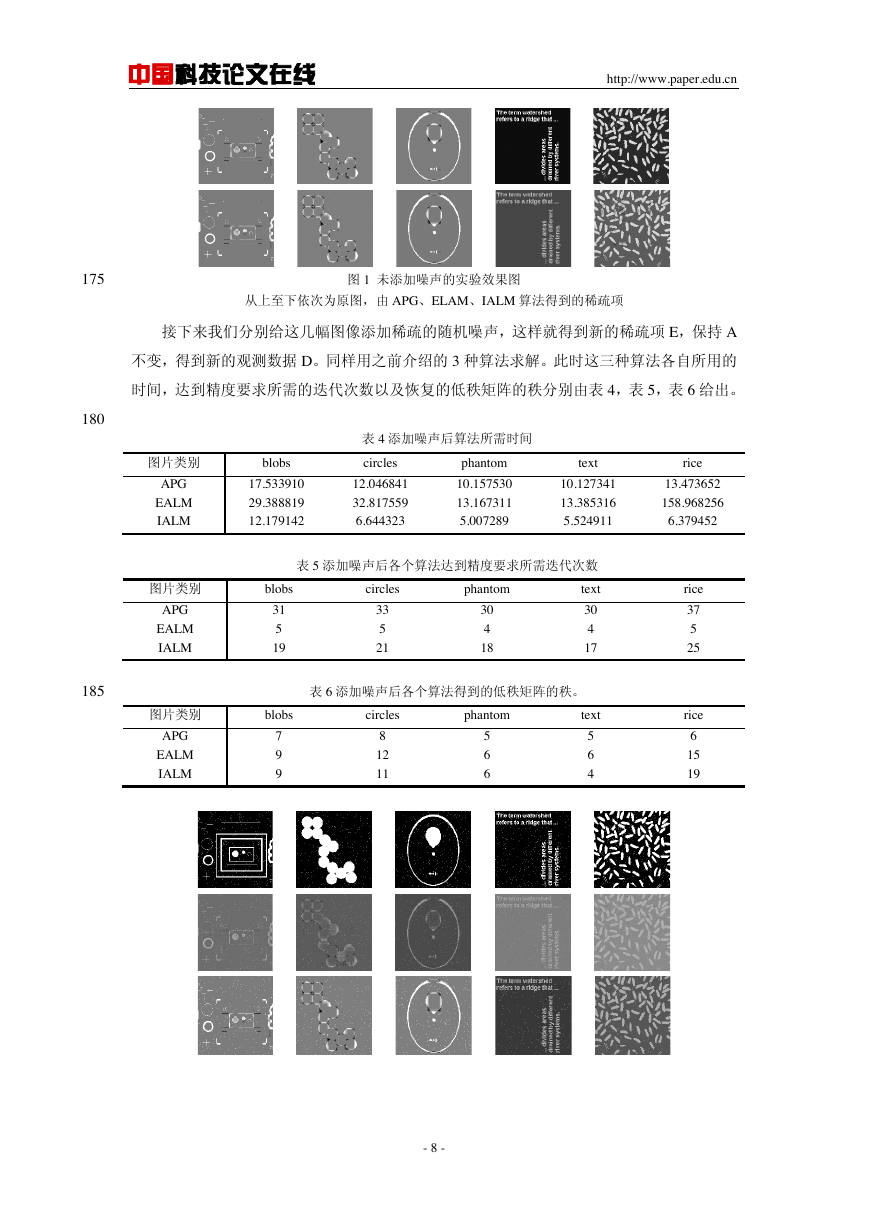
中国科技论文在线 http://www.paper.edu.cn 175 图 1 未添加噪声的实验效果图从上至下依次为原图，由 APG、ELAM、IALM 算法得到的稀疏项接下来我们分别给这几幅图像添加稀疏的随机噪声，这样就得到新的稀疏项 E，保持 A 不变，得到新的观测数据 D。同样用之前介绍的 3 种算法求解。此时这三种算法各自所用的时间，达到精度要求所需的迭代次数以及恢复的低秩矩阵的秩分别由表 4，表 5，表 6 给出。 180 图片类别 APG EALM IALM 图片类别 APG EALM IALM 图片类别 APG EALM IALM 185 表 4 添加噪声后算法所需时间 blobs circles phantom text rice 17.533910 29.388819 12.179142 12.046841 32.817559 6.644323 10.157530 13.167311 5.007289 10.127341 13.385316 5.524911 13.473652 158.968256 6.379452 表 5 添加噪声后各个算法达到精度要求所需迭代次数 blobs circles phantom text rice 31 5 19 33 5 21 30 4 18 30 4 17 37 5 25 表 6 添加噪声后各个算法得到的低秩矩阵的秩。 blobs circles phantom text rice 7 9 9 8 12 11 5 6 6 5 6 4 6 15 19 - 8 - Density: 0.08Rel-Err: 9.52e-004Density: 0.15Rel-Err: 1.27e-004Density: 0.08Rel-Err: 6.64e-004Density: 0.08Rel-Err: 1.55e-004Density: 0.35Rel-Err: 6.32e-004Density: 0.07Rel-Err: 8.44e-004Density: 0.13Rel-Err: 8.51e-004Density: 0.07Rel-Err: 9.22e-004Density: 0.08Rel-Err: 7.51e-004Density: 0.41Rel-Err: 8.41e-004Density: 0.09Rel-Err: 7.35e-002Density: 0.17Rel-Err: 6.94e-002Density: 0.10Rel-Err: 7.39e-002Density: 0.11Rel-Err: 6.81e-002Density: 0.39Rel-Err: 5.30e-002Density: 0.08Rel-Err: 8.91e-004Density: 0.15Rel-Err: 1.35e-004Density: 0.08Rel-Err: 4.31e-004Density: 0.10Rel-Err: 4.77e-004Density: 0.39Rel-Err: 8.56e-005

分享到：

赞收藏

资料库

鲁棒主成分分析算法综述.pdf

相关推荐

开发技术

热门标签

最新资料