2019年吉林省大学生数学建模_CBA 球队夺冠问题.pdf-资料库

hom158-12201334-4744300845173288522.pdf-第1页.png

第1页 / 共36页

hom158-12201334-4744300845173288522.pdf-第2页.png

第2页 / 共36页

hom158-12201334-4744300845173288522.pdf-第3页.png

第3页 / 共36页

hom158-12201334-4744300845173288522.pdf-第4页.png

第4页 / 共36页

hom158-12201334-4744300845173288522.pdf-第5页.png

第5页 / 共36页

hom158-12201334-4744300845173288522.pdf-第6页.png

第6页 / 共36页

hom158-12201334-4744300845173288522.pdf-第7页.png

第7页 / 共36页

hom158-12201334-4744300845173288522.pdf-第8页.png

第8页 / 共36页

2019 年吉林省大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》（2019 年修订版，以下简称为“竞赛章程和参赛规则”，可从全国大学生数学建模竞赛网站下载）。省赛同国家章程和规则。我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。我们知道，抄袭别人的成果是违反竞赛章程和参赛规则的，如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。我们郑重承诺，严格遵守竞赛章程和参赛规则，以保证竞赛的公正、公平性。如有违反竞赛章程和参赛规则的行为，我们将受到严肃处理。我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。我们参赛选择的题号是（从 A/B 中选择一项填写）： A 我们的报名参赛队号为（12 位数字组成的编号）：201907001189 所属学校（请填写完整的全名）：吉林大学参赛队员 (打印并签名) ：1. 刘星宏 2. 李沅津 3. 纪泓宇指导教师或指导教师组负责人 (打印并签名)：（论文纸质版与电子版中的以上信息必须一致，只是电子版中无需签名。以上内容请仔细核对，提交后将不再允许做任何修改。如填写错误，论文可能被取消评奖资格。）日期： 2019 年 4 月 21 日赛区评阅编号（由赛区组委会评阅前进行编号）：

2019 年吉林省大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：赛区评阅记录（可供赛区评阅时使用）：评阅人评分备注

对于 CBA 球队夺冠问题的建模摘要中国男子篮球职业联赛（China Basketball Association），简称（CBA 联赛），是由中国篮球协会所主办的跨年度主客场制篮球联赛。本模型先通过给出的 100 组数据，使用经遗传算法优化的 BP 神经网络进行预测，从而得出每支球队的 500 组预测数据，经正态分布检验后发现所得的预测数据及历史数据符合正态分布，再使用蒙特卡洛法，根据 14 支球队 500 组预测数据，算出各队进入前八强的概率，再通过此概率建议季后赛淘汰模型，并使用蒙特卡洛法统计出每个球队的夺冠概率。为定性分析中国 CBA 联赛十四支球队的水平，我们根据历史临场发挥评分建立实力正态分布函数进行实力排名，模拟建立定性分析模型将球队分为 4 个梯队，以及使用上升潜力模型来优化模型。现实中的 CBA 球队的胜率及球队实力，与球队数据息息相关，本文通过对球队数据中的二分命中率、三分命中率、罚球命中率、篮板、助攻、抢断、盖帽、犯规等因素建立多元线性回归分析模型，从而确立对球队的胜率及球队实力影响大的多个关键因素，从而针对性地对 14 支球队提出建议，以提高球队的夺冠概率。最后，我们对模型的优缺点进行了评价，讨论了其推广应用的价值。关键字：BP 神经网络，遗传算法，蒙特马洛，定性分析模型，多元线性回归分析，逐步分析，MATLAB。 1

一、问题的重述问题的背景：CBA 自每年的 10 月或 11 月开始至次年的 4 月左右结束，截至 2017-2018 赛季，总共有七支球队夺得过总冠军，八一队和广东队都曾八次夺冠，北京队夺得三冠，上海队、四川队、新疆队、辽宁队各夺冠一次。现在疆粤大战总决赛也在如火如荼的进行着。各个地方都有自己的家乡球队，对家乡球队的支持让更多人关注 CBA 球队的排名与冠军球队。问题的提出：假设今年 CBA 联赛有 14 支球队进行常规赛和季后赛两个阶段进行，通过 14 支球队近 100 场的历史临场发挥水平综合评分数据探讨各队的夺冠概率，预测前 4 名的球队并结合具体情况定性分析 14 支球队的水平，最后对于前 4 支球队关于如何最大概率夺冠的合理化建议。二、模型假设（1）每支队伍在比赛期间阵容齐整，球员身体健康，不存在球员受伤或离队情况；（2）裁判判罚尺度分明，执法公平公正；（3）每个球员都有良好的职业操守，每场比赛均能全力以赴，不存在打假球的情况；（4）不考虑主客场，天气等无法控制因素；三、符号说明 σ -- 为成绩的标准差 E -- 为成绩的平均值 v = （标准差/平均值） = σ/E -- 为成绩的变异系数 μ -- 数学期望 2R --拟合优度 F --统计量 P --显著性四、问题分析及模型建立 4.1 正态分布若随机变量 X 服从一个数学期望为μ、方差为σ^2 的正态分布，记为 N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当 μ = 0,σ = 1 时的正态分布是标准正态分布。这是一个关于篮球比赛结果预测的问题，总共有 14 支队伍，由于 CBA 常规赛每个队伍有 46 场比赛，比赛数量较大，所以球队成绩与球队的能力应呈现正相关，即可先通过平均值、标准差、变异系数构建一个大致体现球队能力的函数来判断常规赛排名。通过计算变异系数 v 的值，可以判断考试成绩的稳定性：v 值小表示平均成绩高,成绩的标准差小，预示成绩高并且成绩稳定！v 值大成绩的方差大，每次成绩飘忽不定。 2

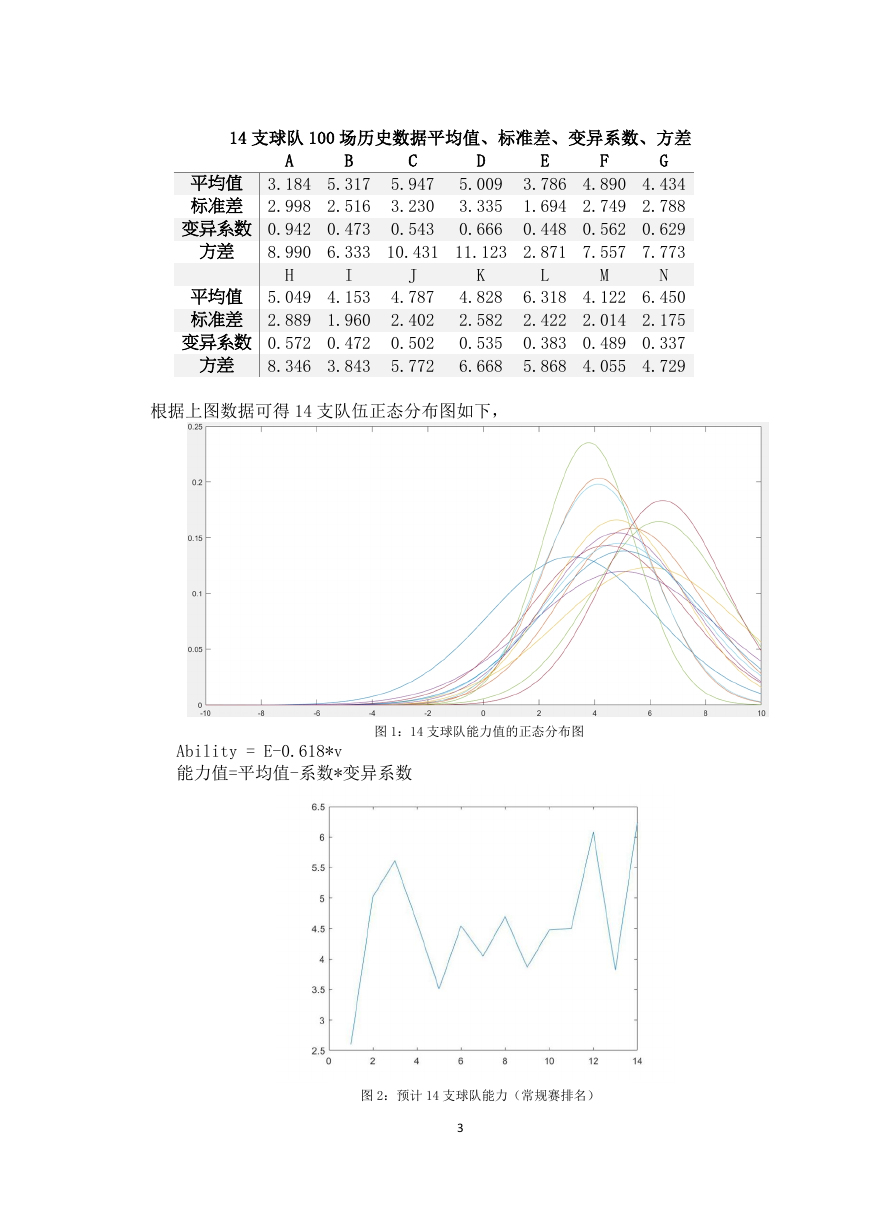
14 支球队 100 场历史数据平均值、标准差、变异系数、方差 A B C D E F G 平均值 3.184 5.317 5.947 5.009 3.786 4.890 4.434 标准差 2.998 2.516 3.230 3.335 1.694 2.749 2.788 变异系数 0.942 0.473 0.543 0.666 0.448 0.562 0.629 8.990 6.333 10.431 11.123 2.871 7.557 7.773 方差 H I J K L M N 平均值 5.049 4.153 4.787 4.828 6.318 4.122 6.450 标准差 2.889 1.960 2.402 2.582 2.422 2.014 2.175 变异系数 0.572 0.472 0.502 0.535 0.383 0.489 0.337 8.346 3.843 5.772 6.668 5.868 4.055 4.729 方差根据上图数据可得 14 支队伍正态分布图如下，图 1：14 支球队能力值的正态分布图 Ability = E-0.618*v 能力值=平均值-系数*变异系数图 2：预计 14 支球队能力（常规赛排名） 3

4.2 基于遗传算法改进的 BP 神经网络预测模型使用遗传算法改进的 BP 神经网络(代码见附录 XX)，能较好地消去单纯地使用 BP 神经网络对于无序的正态分布数组学习后所预测数据产生的奇异点(预测评分>100 或预测评分 <-100)，同时对于原有数据也具有较好的拟合性，即既不会过拟合也不会欠拟合。以 M 队的 96 组数据学习后所形成的模型为例，经正态分布检验我们可以发现 M 队的 96 组评分符合正态分布，再分析现实中的 CBA 球队数据可知，CBA 球队的二分命中率、三分命中率、篮板、抢断、盖帽、失误和犯规等数据均符合正态分。故使用正态分布产生的二分命中率、三分命中率、篮板、抢断、盖帽、失误和犯规等数据作为 BP 神经网络的输入点，将球队场次评分作为输出点，可以预测出 M 队的未来 100 场评分数据，且此 100 场评分数据符合正态分布，其平均值和标准差也基本与历史数据中的 100 组评分数据相符。为尽可能地消除随机性对预测评分的影响，每组球队共预测 5 次未来场次的评分，每组球队有 500 组未来场次评分(预测结果见文件夹中的”各球队 500 场预测数据.xlsx”)。 TOTALSCORE 总得分，通过图 3：BP 神经网络结构图输入点名称及含义 BACKBOARD 篮板，通过正态分布随机数得出. totalScore=exp(2.2924*twoPointHitRate+0.421*onePo intHitRate+0.2617*log(backBoard)+0.1679*log(fault )+1.8088)得出 backBoard = normrnd(46,2.7,1,200); totalElse = block+steal; totalLose = (-1).*(fault+foul); TOTALELSE 二次运动得分，通过盖帽和抢断得出。 TOTALLOSE 二次运动失分，通过失误和犯规得出。以下是此模型对 M 队某一次预测的结果 4

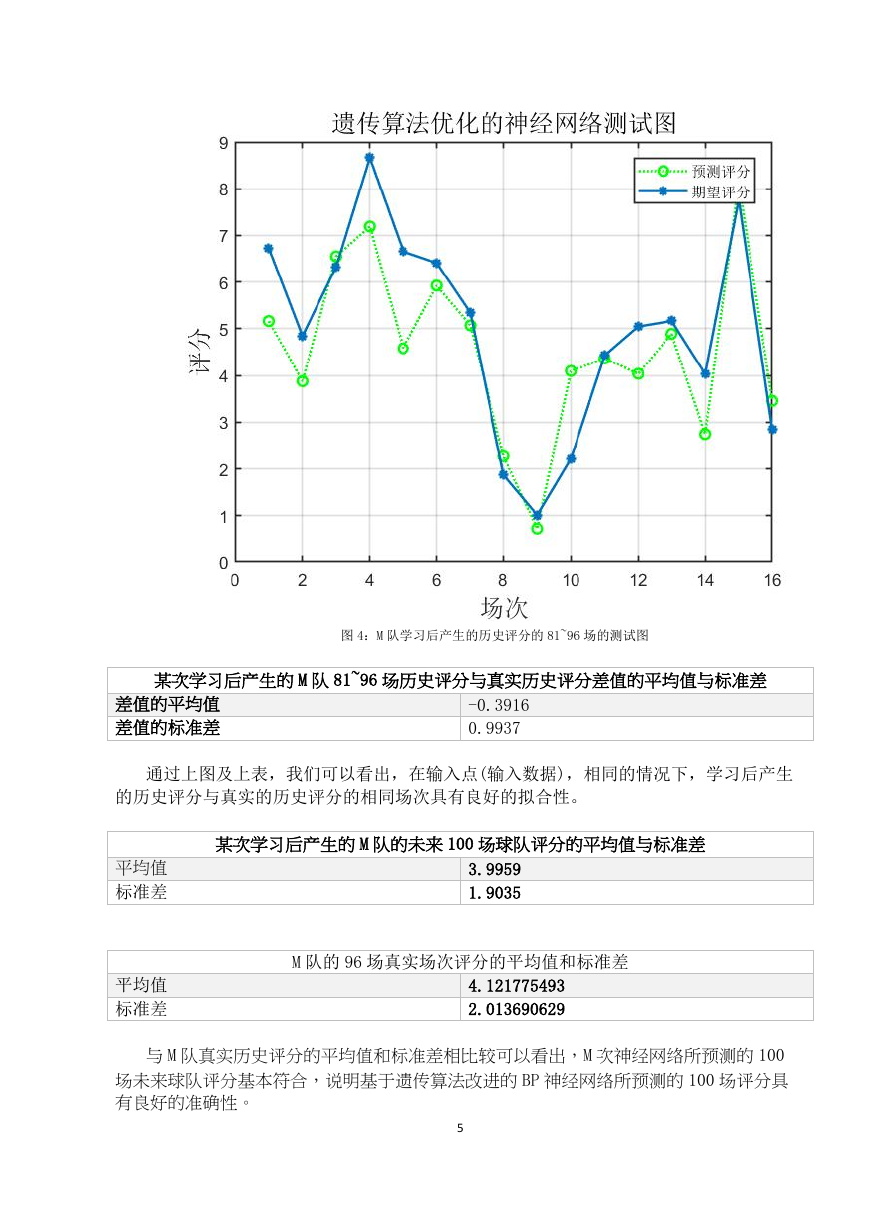
某次学习后产生的 M 队 81~96 场历史评分与真实历史评分差值的平均值与标准差图 4：M 队学习后产生的历史评分的 81~96 场的测试图差值的平均值差值的标准差 -0.3916 0.9937 通过上图及上表，我们可以看出，在输入点(输入数据)，相同的情况下，学习后产生的历史评分与真实的历史评分的相同场次具有良好的拟合性。平均值标准差平均值标准差某次学习后产生的 M 队的未来 100 场球队评分的平均值与标准差 3.9959 1.9035 M 队的 96 场真实场次评分的平均值和标准差 4.121775493 2.013690629 与 M 队真实历史评分的平均值和标准差相比较可以看出，M 次神经网络所预测的 100 场未来球队评分基本符合，说明基于遗传算法改进的 BP 神经网络所预测的 100 场评分具有良好的准确性。 5

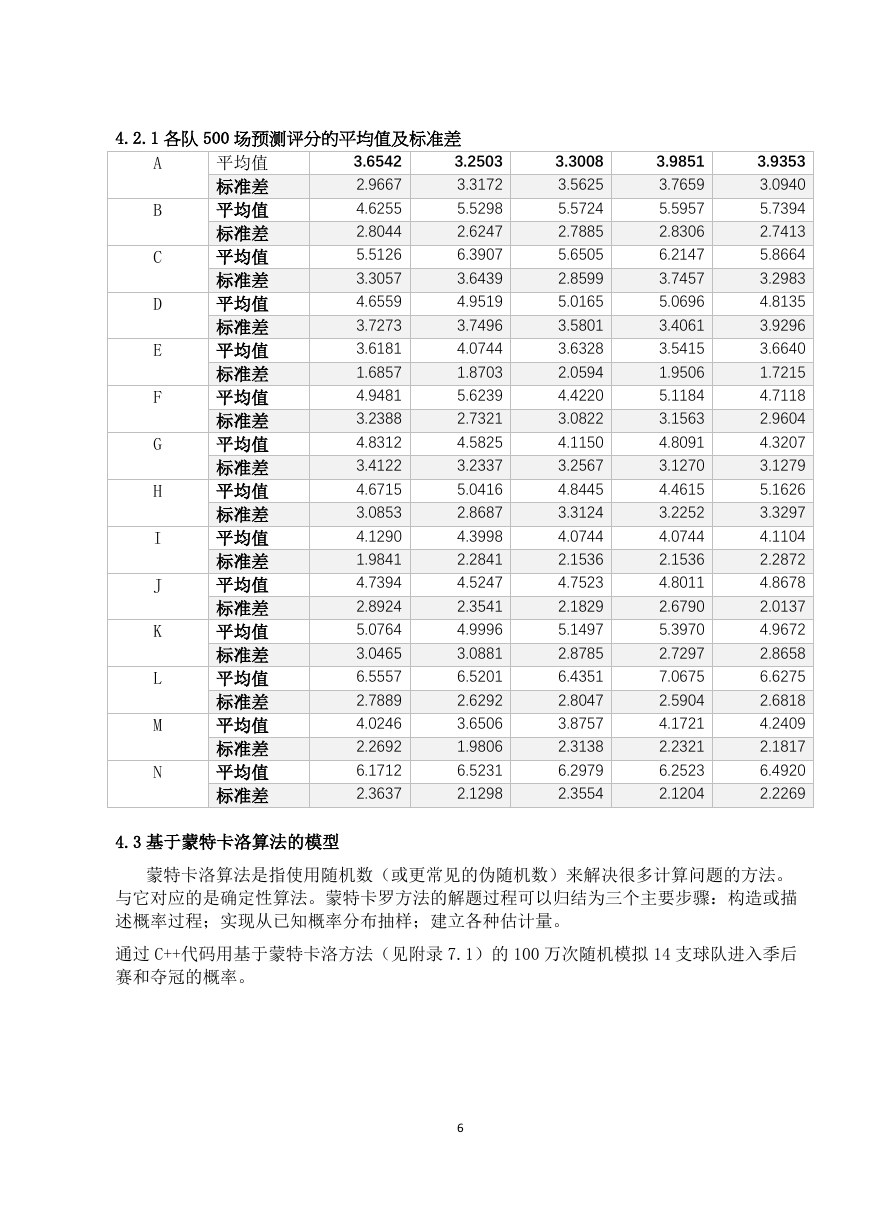
4.2.1 各队 500 场预测评分的平均值及标准差 A B C D E F G H I J K L M N 平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差平均值标准差 3.6542 2.9667 4.6255 2.8044 5.5126 3.3057 4.6559 3.7273 3.6181 1.6857 4.9481 3.2388 4.8312 3.4122 4.6715 3.0853 4.1290 1.9841 4.7394 2.8924 5.0764 3.0465 6.5557 2.7889 4.0246 2.2692 6.1712 2.3637 3.2503 3.3172 5.5298 2.6247 6.3907 3.6439 4.9519 3.7496 4.0744 1.8703 5.6239 2.7321 4.5825 3.2337 5.0416 2.8687 4.3998 2.2841 4.5247 2.3541 4.9996 3.0881 6.5201 2.6292 3.6506 1.9806 6.5231 2.1298 3.3008 3.5625 5.5724 2.7885 5.6505 2.8599 5.0165 3.5801 3.6328 2.0594 4.4220 3.0822 4.1150 3.2567 4.8445 3.3124 4.0744 2.1536 4.7523 2.1829 5.1497 2.8785 6.4351 2.8047 3.8757 2.3138 6.2979 2.3554 3.9851 3.7659 5.5957 2.8306 6.2147 3.7457 5.0696 3.4061 3.5415 1.9506 5.1184 3.1563 4.8091 3.1270 4.4615 3.2252 4.0744 2.1536 4.8011 2.6790 5.3970 2.7297 7.0675 2.5904 4.1721 2.2321 6.2523 2.1204 3.9353 3.0940 5.7394 2.7413 5.8664 3.2983 4.8135 3.9296 3.6640 1.7215 4.7118 2.9604 4.3207 3.1279 5.1626 3.3297 4.1104 2.2872 4.8678 2.0137 4.9672 2.8658 6.6275 2.6818 4.2409 2.1817 6.4920 2.2269 4.3 基于蒙特卡洛算法的模型蒙特卡洛算法是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。与它对应的是确定性算法。蒙特卡罗方法的解题过程可以归结为三个主要步骤：构造或描述概率过程；实现从已知概率分布抽样；建立各种估计量。通过 C++代码用基于蒙特卡洛方法（见附录 7.1）的 100 万次随机模拟 14 支球队进入季后赛和夺冠的概率。 6

资料库

2019年吉林省大学生数学建模_CBA 球队夺冠问题.pdf

相关推荐

考试认证

热门标签

最新资料