2017一2018年广东中山大学规划运筹考研真题.doc

发布时间：2022-09-15 发布人：admin 分类：说明书资料大小：0.19M 资料格式：doc 举报版权申诉

第1页 / 共3页

2017一2018年广东中山大学规划运筹考研真题.doc.pdf-第2页.jpg

第2页 / 共3页

2017一2018年广东中山大学规划运筹考研真题.doc.pdf-第3页.jpg

第3页 / 共3页

文本预览

2017 一 2018 年广东中山大学规划运筹考研真题 2017 年广东中山大学规划运筹考研真题 1、图解法分析线性规划问题在 b 值不确定的约束条件下的最优解变化。分析特定条件下 b 的范围。 2、只有一个约束条件的 LP 问题。要求直接写出原问题的对偶问题，通过观察写出对偶问题的解，再用互补松弛性写出原问题的解。 3、与单纯形法矩阵描述相关。题目给出 LP 问题及其不完整的最终单纯形表，要求用单纯形法矩阵形式的知识求解其中空格的数字，要求有步骤。 4、最短路与最小费用流以及 LP 问题结合。题目给出一个网络图，没方向，只有长度。要求分析此最短路问题并将其表述为最小费用流问题，在此基础上描述成线性规划问题。 5、线性规划建模。生产仓储费用的，只建模不求解。 2018 年广东中山大学规划运筹考研真题 1.考虑下面的线性规划问题: maxZ=cTx s.t.Ax≤b， x≥0，其中 c=（c1，c2，…，cn）T 表示目标函数系数，x=（x1，x2，…，xn）T 表示决策变量向量，A 是 m×n 的矩阵，b=（b1，b2，…，bm）T 表示右端项。证明最优解构成的集合是凸集。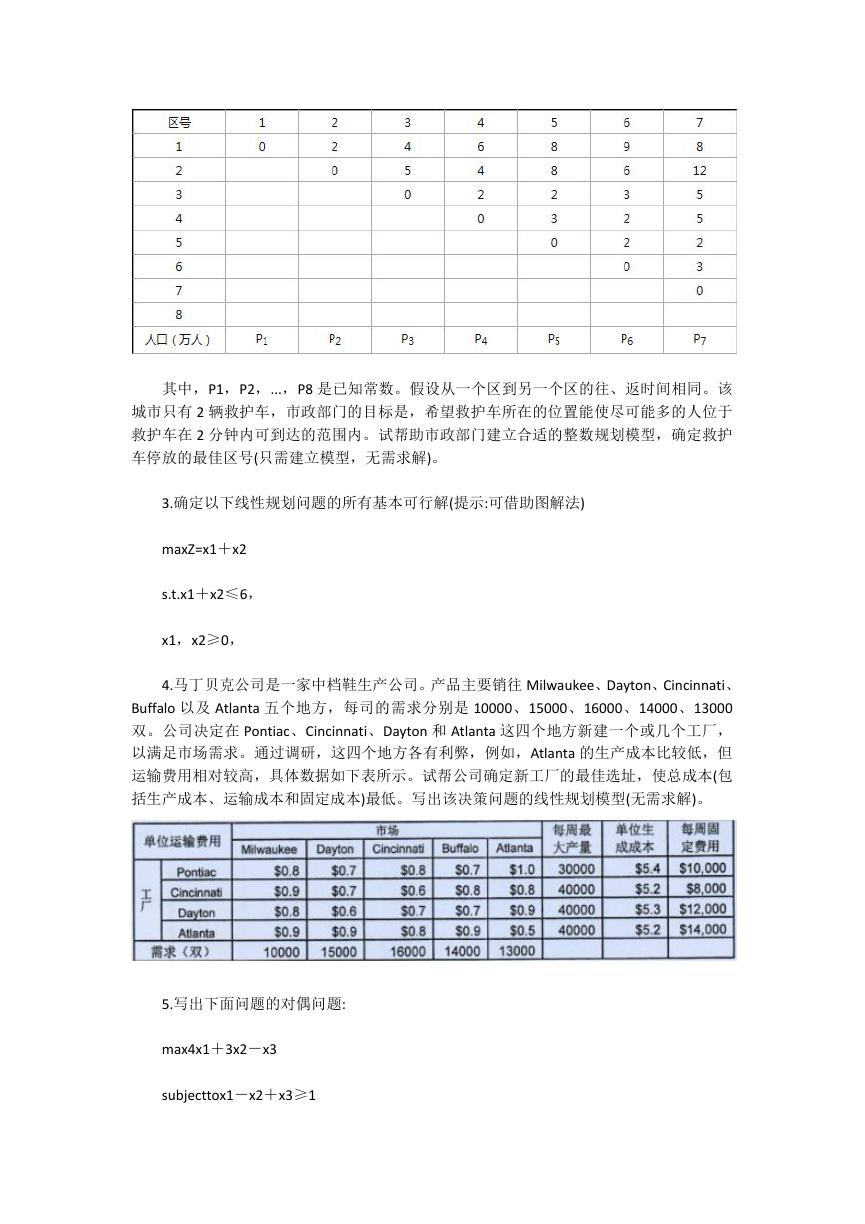 2.某城市有 8 个区，救护车由一个区开到另一个区所需的时间(分钟)如下表所示:

其中，P1，P2，...，P8 是已知常数。假设从一个区到另一个区的往、返时间相同。该城市只有 2 辆救护车，市政部门的目标是，希望救护车所在的位置能使尽可能多的人位于救护车在 2 分钟内可到达的范围内。试帮助市政部门建立合适的整数规划模型，确定救护车停放的最佳区号(只需建立模型，无需求解)。 3.确定以下线性规划问题的所有基本可行解(提示:可借助图解法) maxZ=x1＋x2 s.t.x1＋x2≤6， x1，x2≥0， 4.马丁贝克公司是一家中档鞋生产公司。产品主要销往 Milwaukee、Dayton、Cincinnati、 Buffalo 以及 Atlanta 五个地方，每司的需求分别是 10000、15000、16000、14000、13000 双。公司决定在 Pontiac、Cincinnati、Dayton 和 Atlanta 这四个地方新建一个或几个工厂，以满足市场需求。通过调研，这四个地方各有利弊，例如，Atlanta 的生产成本比较低，但运输费用相对较高，具体数据如下表所示。试帮公司确定新工厂的最佳选址，使总成本(包括生产成本、运输成本和固定成本)最低。写出该决策问题的线性规划模型(无需求解)。 5.写出下面问题的对偶问题: max4x1＋3x2－x3 subjecttox1－x2＋x3≥1

x1＋2x2－3x3≤2 -5x1＋8x3＝5 x1≥0，x2≥0，x3 无拘束 6.用割平面法解下面整数规划问题 minx1－x2 subjecttox1＋x2≤10 -x1＋x2≤5 x1x2≥0，且为整数

分享到：

赞收藏

资料库

2017一2018年广东中山大学规划运筹考研真题.doc

相关推荐

考研

热门标签

最新资料