基于频域滤波数字均衡器的设计 基于频域滤波数字均衡器的设计 为了解决多频段数字均衡滤波器处理过程中数据计算量的问题，通过对数字均衡器设计的分析，将数字音频信 号进行频域滤波处理，最终设计出一种高效的数字均衡滤波器。通过将数字信号在频域中进行傅里叶变换，提 出了一种基于快速傅里叶变换原理的算法，该算法中码位倒置和蝶形运算方法的处理与通常的快速傅里叶变换 相比，更有效地减少了数据的运算量，减少了数据处理的时间。结果表明，使用该种算法设计的数字均衡滤波 器与传统的时域滤波方法相比，具有很好的实时处理效果。 在音频处理中， 常采用的均衡器算法是使用IIR或者FIR 1 设计原理 设计原理 均衡器的基本功能就是调节信号各段频率的强弱，从而弥补信号在传输过程中的缺陷或是达到特定的声音处理效果。因此 为了达到这个目的，调节信号的各段频率可以将输入的信号进行以下处理： 1)对输入的信号进行快速傅里叶变换，使得各个频段的信号分开； 2)对需要变化的频点及其周围的频点进行相应的处理； 3)将处理后的信号进行傅里叶反变换，得到最后需要的信号。 2 傅里叶变换 傅里叶变换 快速傅里叶变换的时域抽取方法是将输入的信号按奇偶分开，打乱原来的顺序，之后进行蝶形运算，以保证输出的序列是 按着时间顺序排列的。分解过程遵循两条规则：1)对时间进行偶奇分解，即码位倒置；2)对频率进行前后分解，即蝶形运算。 2．．1 码位倒置 码位倒置 将长度为Ⅳ的时域序列x(n)按n的奇偶分为两组，变成两个N／2序列 码位倒置可以将输入数据依照奇偶分开，如表1所示。 2．．2 蝶形运算 蝶形运算 2．．2．．1 蝶形运算的原理 蝶形运算的原理 蝶形变换是将处理的信号进行分级处理，逐次进行DFT变换，以减少复数的乘法减少运算次数。对于输入x(n)序列奇偶按分 开的两个序列的DFT运算分别是 2．．2．．2 蝶形运算的算法 蝶形运算的算法 蝶形运算是逐级运算累加实现的，在传统的蝶形运算中，旋转因子 的N是保持一个固定的值而k是不断变化的，第一级到 级中，k的变化是以2为底的幂指数的变化，而到第 级时，k的变化则是0，1，…，(N／2)-1。如果依照k的这种变 第 化规律，在第 级时，就很难继续依照前 级进行变化。因此，根据以上分析，采用另外一种思路来对蝶形运算进行重 新的整理。在旋转因子 中，N是每个 

蝶形单元输入数据的个数，k的变化规律是0，1，…，(N／2)-1，采用这种方法就可以有效的缩短代码的长度，提高运行速 度。图1为蝶形运算流程图。 2．．3 快速傅里叶变换的实现 快速傅里叶变换的实现 蝶形运算的旋转因子 程中，旋转因子和输入数据的计算过程是将实数和复数分开计算所得到的。 因为旋转因子 中k=0，1，…，(N／2)-1，因此随着k的增长cos(-2Pik／N)和sin(-2Pik／N)也相继发生成倍的变化。 对这一现象采用的处理方法是使用正余弦的倍角公式： ，输入的复数表示为InputData=RealInData+j*ImagInData，因此在计算过 这样，处理 的变化的过程就变为处理正弦和余弦倍角变化的过程，从而简化了程序。部分程序如下： 其中，Block是每一个蝶形单元输入个数的一半即N／2，r0和i0分别是旋转因子的实部和虚部。 3 均衡处理 均衡处理 对于频点的调节是调节频点周围这一段的频率幅度的大小，以最终达到调节频率的目的。为了防止在抽取频点时，因某一 点的调节范围过大而使这一段的声音听起来不和谐，在对频点进行调节时，采用的方法是调节该频点及其附近的频点以达到最 终的调节效果。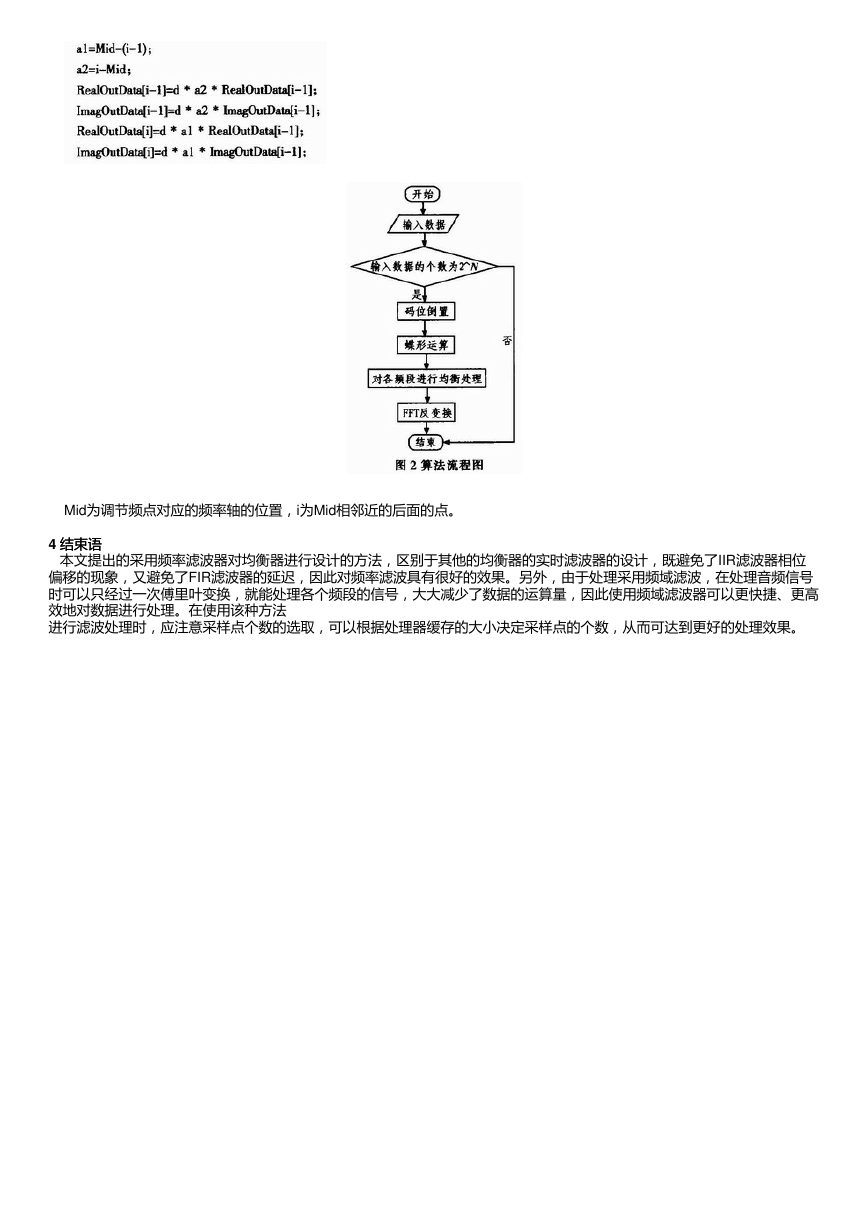 算法的实现：取频率点周围的点，将所取的点调节的范围是该点与对应频率点的距离的反比，这样就避免该点频率的影响 太强烈。算法流程如图2所示。针对某一个频点的处理的程序如下： 

Mid为调节频点对应的频率轴的位置，i为Mid相邻近的后面的点。 4 结束语结束语 本文提出的采用频率滤波器对均衡器进行设计的方法，区别于其他的均衡器的实时滤波器的设计，既避免了IIR滤波器相位 偏移的现象，又避免了FIR滤波器的延迟，因此对频率滤波具有很好的效果。另外，由于处理采用频域滤波，在处理音频信号 时可以只经过一次傅里叶变换，就能处理各个频段的信号，大大减少了数据的运算量，因此使用频域滤波器可以更快捷、更高 效地对数据进行处理。在使用该种方法 进行滤波处理时，应注意采样点个数的选取，可以根据处理器缓存的大小决定采样点的个数，从而可达到更好的处理效果。