logo资料库

东北大学数值分析实验报告.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.98M 资料格式：doc 举报 版权申诉
第1页 / 共25页
第2页 / 共25页
第3页 / 共25页
第4页 / 共25页
第5页 / 共25页
第6页 / 共25页
第7页 / 共25页
第8页 / 共25页
资料共25页，剩余部分请下载后查看
    理 学 院 数 学 系 实 验 报 告 课程名称： 实验学期： 实验班级： 学生学号： 学生姓名： 指导教师： 数值分析 2018-2019 春季学期 软件工程 1704 班 20175283 张志浩 盛莹 理学院数学实验中心 二〇一九年 五月 一 日
    东北大学数学实验中心实验报告规范（暂行） 一、 每个学生每个实验项目一份实验报告。 二、 实验报告内容一般包括以下几个内容： 1. 实验项目名称 2. 实验目的和要求 3. 实验原理 4. 实验内容及步骤 5. 实验数据记录和处理 6. 实验结果与分析（含以上 1、2、3、4、5、6 项，需经指导教师签字认可，附在 实验报告后） 注：各专业各课程的实验报告内容与格式可由指导教师根据实验具体情况做出要求。 三、 实验报告第一页按学院统一的实验报告格式书写，附页用 A4 纸书写，字迹工整， 曲线要画在座标纸上，线路图要整齐、清楚（不得徒手画）。如打印也应采用统一 的实验报告的版头（A4 纸）。 四、 每学期将拟存档的学生实验报告按课程、实验项目分类装订成册，即每个实验 项目每门课程的所有实验报告装订成一本。装订线在左侧，第一页加订实验报告封 皮。 五、 东北大学理学院数学实验报告模板范本，本实验报告双面打印（附后）。
    理学院数学实验中心实验报告 专业： 软件工程 姓名： 张志浩 学号： 20175283 成绩： 实验地点： 图书馆 指导教师签名： 1、实验名称：病态线性方程组的求解（系数矩阵是 Hilbert 矩阵） 2、实验目的: 2.1、掌握 Gauss 消去法求解原理 2.2、掌握 Jacobi 迭代法求解原理 2.3、掌握 G-S 迭代法求解原理 2.4、掌握 SOR 迭代法求解原理 2.5、了解 SOR 迭代法的最优松弛因子 2.6、Jacobi 和 G-S 两种迭代法收敛的充要条件 2.7、了解病态的线性方程组 2.8、掌握误差分析方法实验原理 2.9、比较各种求解方法的优劣 3、实验原理 3.1、Gauss 消去法求解原理 利用顺序高斯消去法进行求解
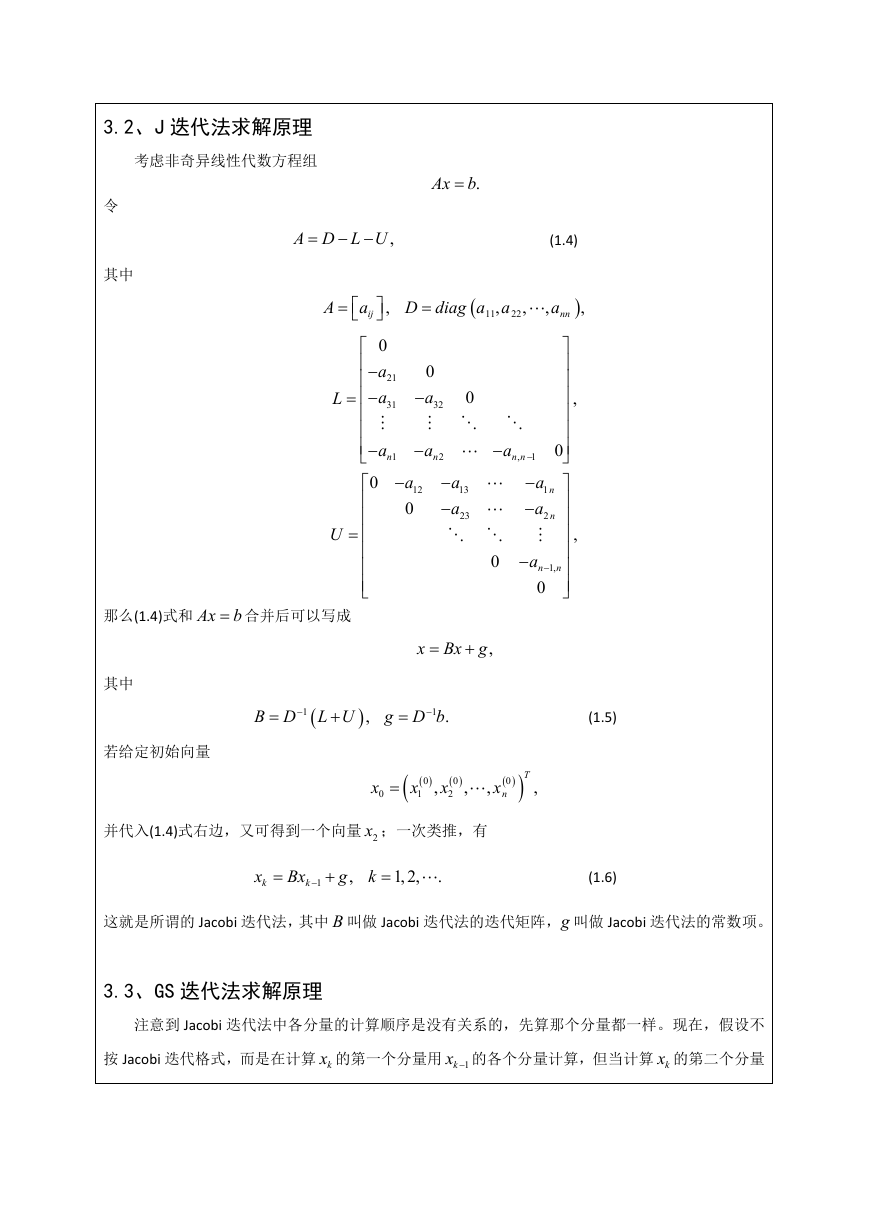
    3.2、J 迭代法求解原理 考虑非奇异线性代数方程组 令 其中 Ax . b , (1.4) A D L U    A  a   , , D diag a a   11 , ,  a nn 22  , L  U  那么(1.4)式和 Ax b 合并后可以写成 ij   0 a 21 a 31  a  0                   1 n   a 12 0 n  0  0 a 32    a a  2 1 , n n a a   1 13 a a      a  1, n 0   0  23 2 n n        0          n , , x Bx g   ,  , 1 g D b   . (1.5) B D L U    1  其中 若给定初始向量 x 0     0 x 1 ,   0 x 2 ,  , x   0 n T  , 并代入(1.4)式右边，又可得到一个向量 2x ；一次类推，有 x k  Bx k 1   g , k .   1,2, (1.6) 这就是所谓的 Jacobi 迭代法，其中 B 叫做 Jacobi 迭代法的迭代矩阵，g 叫做 Jacobi 迭代法的常数项。 3.3、GS 迭代法求解原理 注意到 Jacobi 迭代法中各分量的计算顺序是没有关系的，先算那个分量都一样。现在，假设不 按 Jacobi 迭代格式，而是在计算 kx 的第一个分量用 1kx  的各个分量计算，但当计算 kx 的第二个分量
      kx 时，因   kx 已经算出，用它代替  kx  ，其他分量仍用  1 1 2 ix  。类似地，计算  k 1k lx 时，因  x 1 1 k  ,   k x  1 l , 都已算出，用它们代替  x 1 k  1  ,  1 k  x  1 l ,  , 其他分量仍用 1kx  的分量，于是有 x D Lx D Ux k k   k   1 1  g , k .   1,2, 1  (1.7) 我们称这种迭代格式为 Gauss-Seidel 迭代法，简称为 G-S 迭代法。它的一个明显的好处是在编写程序 是存储量减少了。如果 存在，G-S 迭代法可以改写成  1 D L   x k    1 D L Ux k     D L  1   b . 1  (1.8) 我们把 1L    1 D L U  叫做 G-S 迭代法的迭代矩阵，而把 D L   1 b 叫做 G-S 迭代法的常数项。 3.4、SOR 迭代法求解原理 我们知道，G-S 迭代法的迭代格式为 x k 1   1  D Lx k 现在令 x   x k 1   则有 x , k x k   1 x k x   .  1   1 1 D Ux D b   k . (1.9) 这就是说，对 G-S 迭代法来说， 1kx  可以看作在向量 kx 上加上修正项 x 而得到的。若修正项的前面 加上一个参数，便得到松弛迭代法的迭代格式 x k 1  用分量形式表示即为 x  k  1   x       x k  1  D Lx k  1   1 1 D Ux D b   k (1.10)  , k  1   x i  1     k   x i      i 1   j 1  1   b x ij  k j  n  b x ij 1 i   j    k j g i ,    (1.11) 其中叫做松弛因子。当 1 时，相应的迭代法叫做超松弛迭代法；当 1 时，叫做低松弛迭代 法；当 1 时，就是 G-S 迭代法。我们把超松弛迭代法简称为 SOR 迭代法。 因为 I   1 D L   1 存在，所以(1.10)式可以改写为 其中 x k   1  1     L x k D L    b , L    D  L     1 1    叫做松弛迭代法矩阵。 而 SOR 迭代法收敛的充要条件是 U   D    
    L   1.  (1.12) 由(1.12)式知，SOR 迭代法的谱半径依赖于，当然会问：能否适当选取使收敛速度最快？这就是 选择最佳松弛因子的问题。我写了一个求最优松弛因子的函数，我让从 0 开始增大，每次增大 0.01， 比较谱半径的大小，选择一个让谱半径最小的松弛因子，当 0 增大到了 2，停止 3.5、Jacobi 和 G-S 两种迭代法收敛的充要条件 Jacobi 迭代法和 G-S 迭代法两种迭代法有一个共同的特点，那就是新的近似解 kx 是已知近似解 -1kx 的线性函数，并且只与 -1kx 有关，即它们都可以表示成如下形式： x Mx k k  -1  g . 事实上，对 Jacobi 迭代法，有 对 G-S 迭代法，有 (1.15) .  , 1 g D b   M D L U    1  , M D L U g     1    D L  1   b . 故要求出上述两个迭代法中 kx 有确定的解，且与 -1kx 相对误差较小，就必须说明 kx 用上述两种 迭代法求解时收敛。下面就给出关于上述两种迭代法收敛的证明原理 解方程组的单步线性定常迭代法(1.15)收敛的充分必要条件是其迭代矩阵 M 的谱半径小于 1，即 M   1.  (1.16) 从上述的(1.16)可知，迭代序列收敛取决于迭代矩阵的谱半径，而与初始向量的选取和常数项无关。 4、实验内容及步骤： （考虑到老师不会代码，所以在这里我不展示代码，代码放到附件，但是 这里所展示的大多数结果都是我通过程序算出来的） 调用自己编写的代码（其中包括的 Hilbert 函数以及 b 函数可创建出对应阶数的 H 矩阵以及向量 b，Gauss_Cal 函数、Jacobi_Cal 函数、Gauss_Seidel_Cal 函数、SOR_Cal 函数（该函数自动寻找最优 松弛因子，然后以最优因子进行求解）可完成各自方法的求解），分别取 n = 2,5,10,20,50，对于迭 代法设定终止计算精度为  -210 ，所得计算结果以 16 位有效数字输出，分别见表 2~表 6。 方程组 Hx b 的求解，其中系数矩阵 H 为 Hilbert 矩阵， H  ( h i , ) j n n  , h i , j  1 j   1 i , , i j  1,2, ,  n
    （一）求解 Hx 进行观察） b ，我们暂时选择系数矩阵 H 的维数 6 n  ，所以（在之后我们不断增加 n 的值， H                   1 1 2 1 3 1 4 1 5 1 6 1 2 1 3 1 4 1 5 1 6 1 7 1 3 1 4 1 5 1 6 1 7 1 8 1 4 1 5 1 6 1 7 1 8 1 9 1 5 1 6 1 7 1 8 1 9 1 10 1   6  1   7  1  8 ,   1  9   1  10  1   11  x    1 1 1 1 1 1 ,T b Hx            2.450 1.593 1.218 0.996 0.846 0.737          . 令 x 的各分量都为 1,，即 根据 Hx b 得 而后我们接下来就用 Gauss 消去法、J 迭代法、GS 迭代法和 SOR 迭代法四种迭代法求解                  1 1 2 1 3 1 4 1 5 1 6 1 2 1 3 1 4 1 5 1 6 1 7 1 3 1 4 1 5 1 6 1 7 1 8 1 1 5 4 1 1 6 5 1 1 7 6 1 1 8 7 1 1 9 8 1 1 9 10 1 6 1 7 1 8 1 9 1 10 1 11     2.450     1.593    1.218    x  0.996    0.846    0.737                (1.17) 的解 x。 4.1、Gauss 消去法求解
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料