< 第 25卷第 3期 2005年 3月 　 计算机应用 Computer App lications 文章编号 : 1001 - 9081 (2005) 03 - 0606 - 03 < Ä Äl < < Äl Ä 　 Vol. 25 No. 3 Mar. 2005 基于小波变换的图像增强新算法 周 　旋 ,周树道 ,黄 　峰 ,周小滔 (解放军理工大学 气象学院 ,江苏 南京 211101) ( bambooperfect@163. com ) 摘 　要 :传统的小波增强算法应用于光照不足或不均匀的图像时处理效果一般 ,针对该问题提出 了基于小波变换的图像增强新算法 。首先 ,对图像进行多级小波分解 ,得到尺度系数和多个层次的小 波系数 ;然后 ,对不同层次的小波系数采用不同的增强算法进行处理 ,同时 ,对图像的尺度系数采用多 尺度方法进行处理 ;最后 ,利用得到的小波系数和尺度系数进行小波逆变换 。实验表明 ,该方法无论 是增强效果还是抗噪性能都明显优于传统的图像增强算法 ,同时对光照不足或不均匀的图像具有较 好的处理效果 。 关键词 :小波变换 ;增强 ;对比度 ;小波系数 ;尺度系数 中图分类号 : TP391. 41　文献标识码 : A New a lgor ithm of image enhancem en t ba sed on wavelet tran sform ZHOU Xuan, ZHOU Shu dao, HUANG Feng, ZHOU Xiao tao (College of M eteorology, PLA U niversity of S cience and Technology, N an jing J iangsu 211101, Ch ina) Abstract: Traditional wavelet the shortcom ing, a new wavelet based algorithm has a common effect on the images of light nonuniform ity and scarcity. A im ing at based algorithm for image enhancement was p roposed. The image was first decomposed into multi level wavelet coefficients. Then, every level of wavelet coefficients was enhanced by different algorithm s, and the scaling coefficients were p rocessed by MSR (Multiscale Retinex). Finally, the image of enhancement was obtained via the inverse wavelet transform. Experiments show that the algorithm excels conventional algorithm s in the effect of enhancement and the abatement of noise, at the same time, it has an excellent effect on the images of light nonuniform ity and scarcity. level wavelet to obtain the scaling coefficients and the multi Key words: wavelet transform; enhancement; contrast; wavelet coefficients; scaling coefficients 0　引言 在图像的获取过程中 ,由于传感器噪声 、随机大气湍流和 成像光源的散射等多方面因素 ,图像的分辨率和对比度产生 下降 ,因此 ,为得到一幅清晰的图像 ,必须进行增强处理 。传 统的图像增强算法在改善图像的对比度和增强图像的细节的 同时放大了噪声 ,而小波增强 [ 1, 2 ]在增强图像细节的同时抑 制了图像的噪声 ,该方法通过小波变换使原图像中不同分辨 率的细节特征随尺度的不同而分离 ,然后 ,利用非线性变换函 数对不同尺度小波分量分别进行变换 ,使原始图像中不同分 辨率的细节特征都得到增强 ,然而 ,图像的低频分量即尺度分 量没有作相应改变 ,处理后的图像灰度基本没有变化 。人眼 的光接收体可分为锥状体和杆状体两类 ,锥状体能辨认图像 的细节 ,但在低照度下不起作用 ,杆状体在低照度下起作用 , 但不能感受图像的细节 ,因此 ,在太高或太低的照度下 ,增强 细节意义不大 。 本文提出一种基于小波变换的图像增强新算法 ,利用 àtrous算法 [ 3, 4 ]对图像进行多级小波分解 ,得到图像的小波系 数和尺度系数 ,对尺度系数利用 M SR (M ultiscale Retinex) [ 4 ] 进行处理 ,同时对不同尺度下小波系数利用不同的非线性函 数进行变换 ,最后 ,利用变换后尺度系数和小波系数进行小波 逆变换 。实验表明本文提出的算法无论在增强还是在抗噪方 面都优于传统的图像增强算法 。 1　小波变换 图 1　图像的小波分解和重构 小波变换是利用一系列占据一定时频中心位置的小波函 ( t) 分别为小波函数和 数的叠加来表示信号 。假设 ψ( t) 和 尺度函数 , aj [ n ], d j [ n ]分别为尺度系数和小波系数 : aj [ n ] = < f ( t) , 2 j ( t - n) > 其中 , 2 j ( t) = 1 2 ( t 2j ) , j ≥ 0 dj [ n ] = < f ( t) , ψ2 j ( t - n) > 其中 ,ψ2 j ( t) = ψ( 1 2 t 2j ) , j > 0 对于任何 j ≥ 0 ( àtrous算法 ) : aj+1 [ n ] = aj hj [ n ], dj+1 [ n ] = aj gj [ n ] 且 aj [ n ] = 1 2 ( aj+1 hj [ n ] + dj+1 g [ n ] ) 　　收稿日期 : 2004 - 08 - 04;修订日期 : 2004 - 11 - 05 　　作者简介 :周旋 (1980 - ) ,男 ,河南罗山人 ,硕士研究生 ,主要研究方向 :图像处理、模式识别 ; 　周树道 ( 1963 - ) ,男 ,浙江人 ,副教授 ,硕士 , 主要研究方向 :图像处理、模式识别 ,神经网络 ; 　黄峰 (1955 - ) ,男 ,安徽蚌埠人 ,教授 ,硕士 ,主要研究方向 :图像处理、数据压缩. 

3 第 3期 3 3 3 3 周旋等 :基于小波变换的图像增强新算法 　　　　 706 其中 h, g分别对应低通分解滤波器和高通分解滤波器 , g分别对应低通重建滤波器和高通重建滤波器 。 h, àtrous算法的滤波器组算法类似于没有次采样的快速双 小波系数的增益较大 ;当噪声较大时 ,对小波系数的增益较 小 ,达到自适应增强的目的 。B rown在文献 [ 1 ]中详细地阐述 了噪声显著性指数与小波系数的关系 。 正交小波变换 。 2　基于 M SR的小波增强 文献 [ 5 ]表明边沿细节信息在小波域中对应的系数绝对 值较大 ,据此采用非线性变换函数对小波系数进行变换 ,增强 图像的细节高频信息 ,同时抑制噪声的放大 。在处理的过程 中 ,对小波系数采用了下面三种增强算法 : 1)单阈值增强算法 该算法采用的非线性变换函数如下 : W in + T ( G - 1) , W in > T W in - T ( G - 1) , W in < - T W ou t = G W in , W in < T 其中 , T为阈值门限 , G为增益因子 , W in 和 W ou t 为变换前 后的小波系数 。在实验中 , T和 G的值采用人机交互的方式进 行选取 。该算法对所有的小波系数进行了放大 ,在增强图像细 节的同时 ,对噪声进行了放大 。 2) 双阈值增强算法 该算法采用的非线性变换函数如下 : W ou t = W in + ( T2 ( G - 1) ) - ( T1 G) , W in > T2 G 0, G (W in - T1 ) , (W in + T1 ) , T2 ≥W in > T1 - T1 ≤W in ≤ T1 - T1 > W in ≥ - T2 W in - ( T2 ( G - 1) ) + ( T1 G) , W in < - T2 其中 , T1 和 T2 为阈值门限 ( T1 < T2 ) , T1 取 σ 2logn / n ( n为图像大小 , σ为均方差 ) , G为增益 , W in和 W ou t为变换前 后的小波系数。在实验中 , T2 和 G的值采用人机交互的方式进 行选取。该算法将 - T1 与 T1 间小波系数设为 0,对噪声进行抑 制 ,其他区间的小波系数采用相应的变换函数 ,增强图像细节。 3) 自适应增强算法 该算法采用的非线性变换函数如下 : W ou t = W in , 　　　　　　　　　　　　W in > T2 T2 - G T1 (W in - T2 ) + T2 , T2 ≥W in > T1 - T1 ≤W in ≤ T1 (W in + T1 ) - T2 , - T1 > W in ≥ - T2 W in < - T2 T2 - T1 G W in , T2 - G T1 T2 - T1 W in , 其中 , T1 和 T2 为阈值门限 ( T1 < T2 ) , G为增益 , W in 和 W ou t 为变换前后的小波系数 。在实验中 , T1 和 T2 的值采用人 机交互的方式进行选取 。G与噪声显著性指数 g的关系如下 : Gmax, 　　　　 g ≤ g1 G = Gmax g1 - g2 0, g + g2 , g1 < g < g2 g ≥ g2 g1 和 g2 分别为阈值门限 ( g1 < g2 ) 。当噪声较小时 ,对 由于小波增强对光照不均匀或不足的图像 ,处理效果不 太理想 ,因此 ,在利用小波变换增强图像细节同时必须对图像 进行亮度调整 。 图 2　图像处理流程 MSR (M ultiscale Retinex) [ 6 ]利用人眼的色感一致性对图 像进行处理 ,对灰度图像具有很好的动态范围压缩性能 ,由于 采用多尺度处理 ,对不同照度下的细节都有增强效果 ,处理后 图像的亮度有了明显的改善 。具体的处理方法如下 : N n =1 - log[ F ( x, y) I ( x, y) ]} wn { logI ( x, y) R ( x, y) = ∑ 其中 , R ( x, y) 为 M SR的输出 , I ( x, y) 为图像数据 , 为 卷积运算符 , w n 为权重 ,满足 ∑w n = 1。F ( x, y) 为 Gauss函 ( x2 + y2 ) / c2 ) , k必须 数 ,具体表示如下 : F ( x, y) = k 满足 ∫∫F ( x, y) dxdy = 1, cn 控制高斯曲面的形状 , N 为不同 形状的高斯曲面的数目即为尺度的数目 , 不同的 n对应不同 的 cn 。由于 M SR具有较好的动态范围压缩性能 ,对于光照 不均匀或不足的图像具有较好处理效果 。 exp ( - 再利用小波变换对图像进行增强 ,通过对不同类型和长 度的小波基进行比较 ,选择了长度为 5的 B3样条小波 ,进行 4级小波分解 。对于第一级的小波系数 ,由于噪声主要集中 在这一层 ,采用双阈值增强算法 , 其中 T1 = 3. 5, G = 8;对于 第二 、三级的小波系数 ,由于噪声较小 ,采用自适应增强算法 。 处理第二级小波系数时 , T1 = 3, T2 = 46, G = 10;处理第三级 小波系数时 T1 = 1. 8, T2 = 35, G = 10。对于第四级的小波系 数 ,采用单阈值增强算法进行处理 ,其中 , T = 1. 5, G = 8。对 于尺度系数采用 MSR 进行处理 ,选用三个尺度 , c的取值分 别为 15, 70和 210,权重的取值为 1 /3, 1 /3和 1 /3。 3　实验 实验选择细节较为丰富 coup le和 baboon图像 。对于处 理前后图像对比度的提高 ,采用均方差和对比度提升指数作 为判别标准 。均方差即图像灰度值的均方差 。对比度改善指 数 C II( the contrast imp rovement index)定义为 : C II = Cprocessed /Corig ina l 将图像分为 3 ×3的块 , C为所有 3 ×3小块图像对比度的 (m ax为该块 均值 ,对比度定义为 (m ax - m in) / (m ax + m in) 图像灰度值的最大值 , m in为该块图像灰度值的最小值 ) 。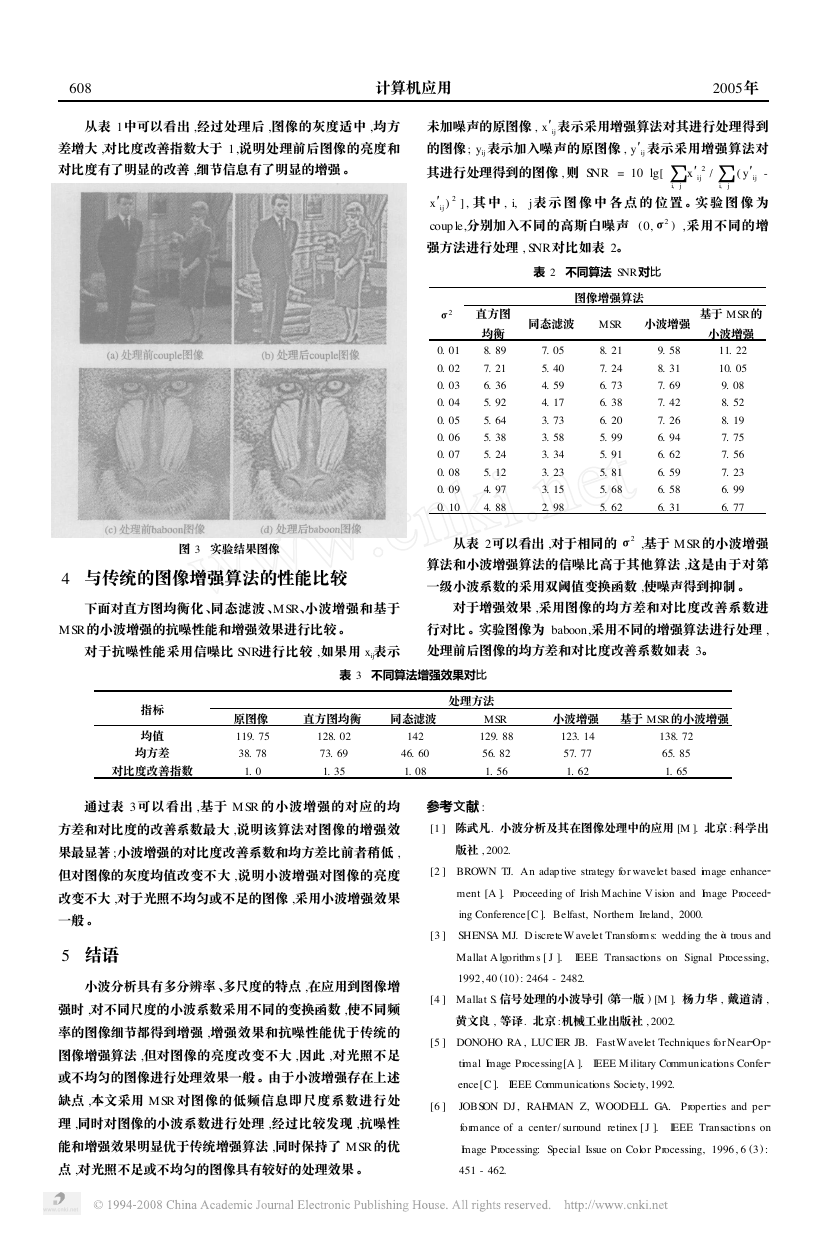 表 1　处理前后图像均值 、均方差和对比度改善指数 图像 均值 均方差 对比度改善指数 coup le (图 3a) coup le (图 3b) baboon (图 3c) baboon (图 3d) 40. 66 107. 66 119. 74 138. 72 34. 96 47. 24 38. 78 65. 85 1. 00 1. 21 1. 00 1. 65 

2 2 2 2 2 2 806　　　　 计算机应用 2005年 　　从表 1中可以看出 ,经过处理后 ,图像的灰度适中 ,均方 差增大 ,对比度改善指数大于 1,说明处理前后图像的亮度和 对比度有了明显的改善 ,细节信息有了明显的增强 。 未加噪声的原图像 , x′ij表示采用增强算法对其进行处理得到 的图像 ; yij表示加入噪声的原图像 , y′ij 表示采用增强算法对 其进行处理得到的图像 , 则 SNR = 10 lg[ ∑ ( y′ij - j表 示 图 像 中 各 点 的 位 置 。实 验 图 像 为 x′ij ) 2 ], 其 中 , i, coup le,分别加入不同的高斯白噪声 ( 0,σ2 ) ,采用不同的增 强方法进行处理 , SNR对比如表 2。 2 / ∑ x′ij i, j i, j 表 2　不同算法 SNR对比 图像增强算法 σ2 0. 01 0. 02 0. 03 0. 04 0. 05 0. 06 0. 07 0. 08 0. 09 0. 10 直方图 均衡 8. 89 7. 21 6. 36 5. 92 5. 64 5. 38 5. 24 5. 12 4. 97 4. 88 同态滤波 MSR 小波增强 基于 MSR的 小波增强 7. 05 5. 40 4. 59 4. 17 3. 73 3. 58 3. 34 3. 23 3. 15 2. 98 8. 21 7. 24 6. 73 6. 38 6. 20 5. 99 5. 91 5. 81 5. 68 5. 62 9. 58 8. 31 7. 69 7. 42 7. 26 6. 94 6. 62 6. 59 6. 58 6. 31 11. 22 10. 05 9. 08 8. 52 8. 19 7. 75 7. 56 7. 23 6. 99 6. 77 图 3　实验结果图像 4　与传统的图像增强算法的性能比较 下面对直方图均衡化 、同态滤波 、MSR、小波增强和基于 MSR的小波增强的抗噪性能和增强效果进行比较 。 对于抗噪性能采用信噪比 SNR进行比较 ,如果用 xij表示 从表 2可以看出 ,对于相同的 σ2 ,基于 MSR的小波增强 算法和小波增强算法的信噪比高于其他算法 ,这是由于对第 一级小波系数的采用双阈值变换函数 ,使噪声得到抑制 。 对于增强效果 ,采用图像的均方差和对比度改善系数进 行对比 。实验图像为 baboon,采用不同的增强算法进行处理 , 处理前后图像的均方差和对比度改善系数如表 3。 表 3　不同算法增强效果对比 指标 均值 均方差 对比度改善指数 原图像 119. 75 38. 78 1. 0 直方图均衡 同态滤波 128. 02 73. 69 1. 35 142 46. 60 1. 08 处理方法 MSR 129. 88 56. 82 1. 56 小波增强 基于 MSR的小波增强 123. 14 57. 77 1. 62 138. 72 65. 85 1. 65 　　通过表 3可以看出 ,基于 M SR 的小波增强的对应的均 方差和对比度的改善系数最大 ,说明该算法对图像的增强效 果最显著 ;小波增强的对比度改善系数和均方差比前者稍低 , 但对图像的灰度均值改变不大 ,说明小波增强对图像的亮度 改变不大 ,对于光照不均匀或不足的图像 ,采用小波增强效果 一般 。 5　结语 小波分析具有多分辨率 、多尺度的特点 ,在应用到图像增 强时 ,对不同尺度的小波系数采用不同的变换函数 ,使不同频 率的图像细节都得到增强 ,增强效果和抗噪性能优于传统的 图像增强算法 ,但对图像的亮度改变不大 ,因此 ,对光照不足 或不均匀的图像进行处理效果一般 。由于小波增强存在上述 缺点 ,本文采用 MSR 对图像的低频信息即尺度系数进行处 理 ,同时对图像的小波系数进行处理 ,经过比较发现 ,抗噪性 能和增强效果明显优于传统增强算法 ,同时保持了 MSR的优 点 ,对光照不足或不均匀的图像具有较好的处理效果 。 参考文献 : [1 ]　陈武凡. 小波分析及其在图像处理中的应用 [M ]. 北京 :科学出 版社 , 2002. [2 ]　BROWN TJ. An adap tive strategy for wavelet based image enhance ment [A ]. Proceeding of Irish Machine V ision and Image Proceed ing Conference[C ]. Belfast, Northern Ireland, 2000. [3 ]　SHENSA MJ. D iscrete W avelet Transform s: wedding the àtrous and Mallat A lgorithm s [ J ]. IEEE Transactions on Signal Processing, 1992, 40 (10) : 2464 - 2482. [4 ]　Mallat S. 信号处理的小波导引 (第一版 ) [M ]. 杨力华 , 戴道清 , 黄文良 , 等译. 北京 :机械工业出版社 , 2002. [5 ]　DONOHO RA , LUC IER JB. FastW avelet Techniques for Near Op timal Image Processing[A ]. IEEE M ilitary Communications Confer ence[C ]. IEEE Communications Society, 1992. [6 ]　JOBSON DJ, RAHMAN Z, WOODELL GA. Properties and per formance of a center/ surround retinex [ J ]. IEEE Transactions on Image Processing: Special Issue on Color Processing, 1996, 6 (3 ) : 451 - 462.