2006年山东青岛建筑工程学院结构力学考研真题.doc

发布时间：2022-09-15 发布人：admin 分类：说明书资料大小：0.75M 资料格式：doc 举报版权申诉

第1页 / 共7页

第2页 / 共7页

第3页 / 共7页

第4页 / 共7页

第5页 / 共7页

第6页 / 共7页

第7页 / 共7页

2006年山东青岛建筑工程学院结构力学考研真题

108/7

228/7228/7

11576

2  43

128

(c)

AFC

1-x/12

x/12

3/4

 3

N l4

 ⎝⎠⎝⎠＝

⎛5 ⎞2

0.237

2.102

 0.02118⎜⎟

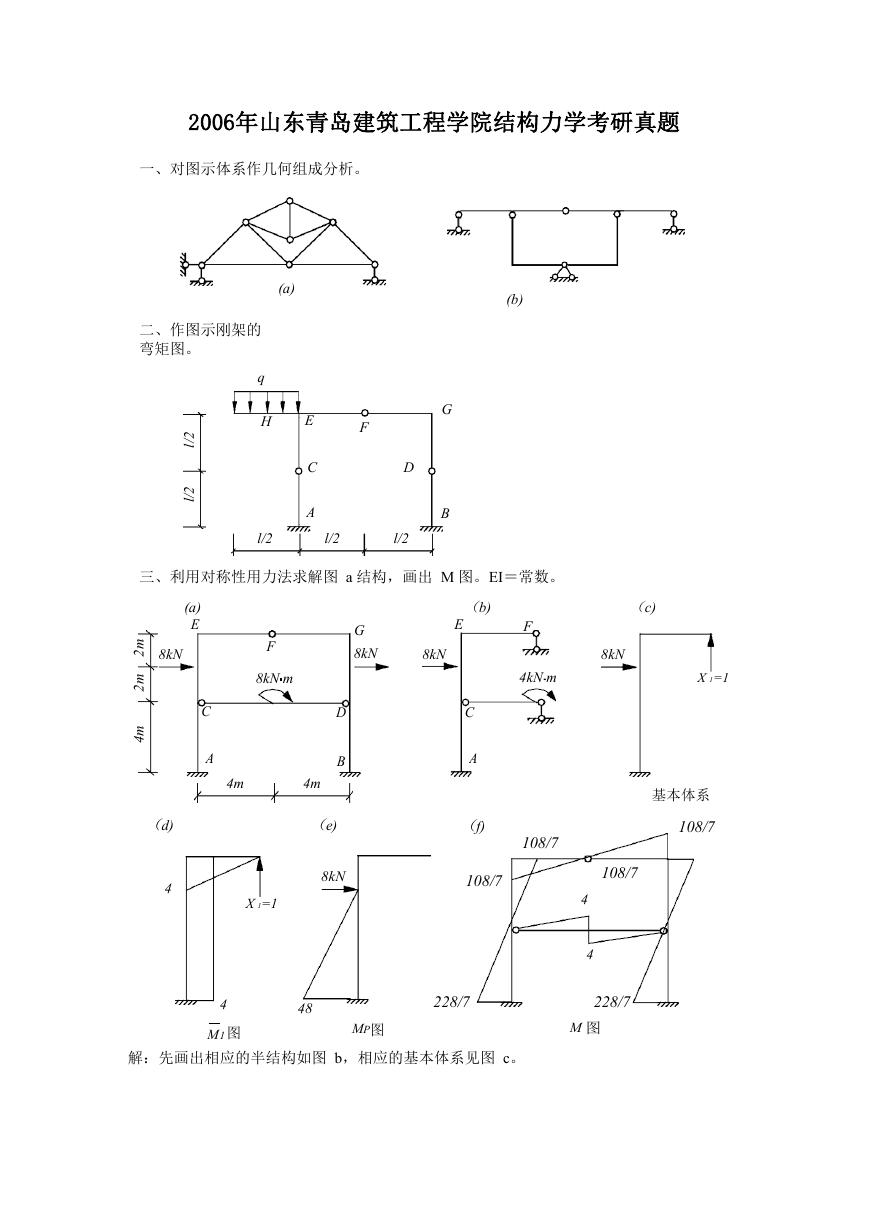
2006年山东青岛建筑工程学院结构力学考研真题一、对图示体系作几何组成分析。 (a) (b) 二、作图示刚架的弯矩图。 q H 2 / l 2 / l E C A F D G B l/2 l/2 l/2 三、利用对称性用力法求解图 a 结构，画出 M 图。EI＝常数。（b) E F G 8kN 8kN （c) 8kN 4kN m X 1=1 C A 108/7 （f) 108/7 基本体系 108/7 108/7 4 4 228/7 M 图 (a) E 8kN m 2 m 2 m 4 C A （d) 4 F 8kN m D B 4m 4m （e) 8kN X 1=1 4 M1 图 48 MP图 228/7 解：先画出相应的半结构如图 b，相应的基本体系见图 c。

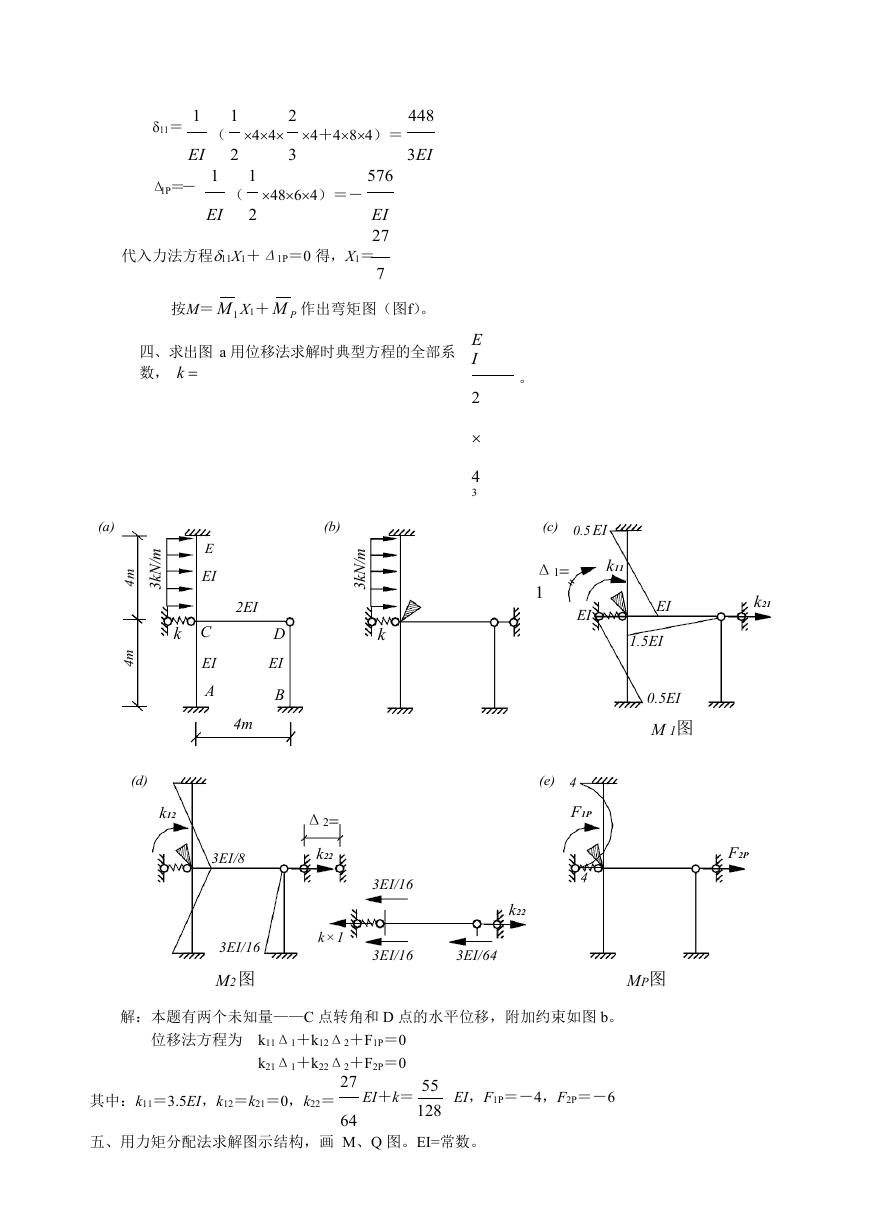
11＝ 1 EI Δ ＝－ 1P 1 2 1 EI 1 2 代入力法方程11X1＋Δ1P＝0 得，X1＝ 2 3 448 3EI （ 44 4＋484）＝（ 4864）＝－ 576 EI 27 7 按M＝ M1 X1＋ M P 作出弯矩图（图f）。四、求出图 a 用位移法求解时典型方程的全部系数， k  。 E I 2  4 3 (b) / m N k 3 k (a) / m N k 3 m 4 E EI m 4 k C EI A 2EI 4m D EI B (d) k12 Δ k22 k×1 3EI/8 3EI/16 M2 图 3EI/16 k22 3EI/16 3EI/64 (c) 0.5 EI k11 Δ  EI (e) 4 F1P 4 EI 1.5EI 0.5EI M 1图 MP图 k21 F2P 解：本题有两个未知量——C 点转角和 D 点的水平位移，附加约束如图 b。位移法方程为 k11Δ1＋k12Δ2＋F1P＝0 k21Δ1＋k22Δ2＋F2P＝0 其中：k11＝3.5EI，k12＝k21＝0，k22＝ 27 64 EI＋k＝ 55 128 EI，F1P＝－4，F2P＝－6 五、用力矩分配法求解图示结构，画 M、Q 图。EI=常数。

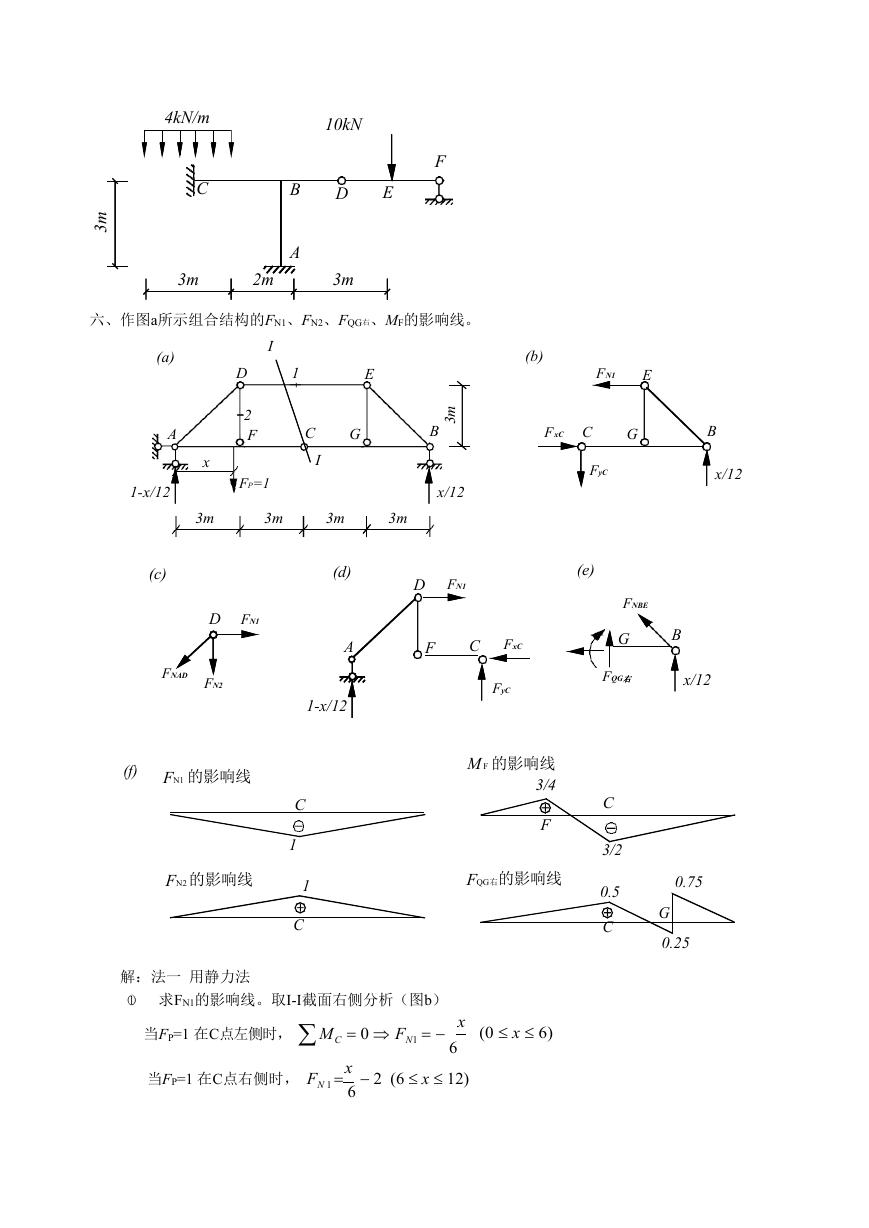
4kN/m C m 3 10kN D E F B A 3m 2m 3m 六、作图a所示组合结构的FN1、FN2、FQG右、MF的影响线。 I D 1 E 2 F FP=1 G C I 3m 3m 3m (a) A 1-x/12 (c) x 3m D FN1 FNAD FN2 (d) A 1-x/12 m 3 B x/12 D FN1 F C FxC FyC (f) FN1 的影响线 FN2 的影响线 C 1 1 C 解：法一用静力法（1）求FN1的影响线。取I-I截面右侧分析（图b）当FP=1 在C点左侧时，  MC  0  FN1   M F 的影响线 3/4 F FQG右的影响线 x 6 (0  x  6) 当FP=1 在C点右侧时， FN 1  x 6  2 (6  x  12) (b) FN1 E F xC C G FyC (e) B x/12 FNBE G FQG右 B x/12 C 3/2 0.5 C 0.75 G 0.25

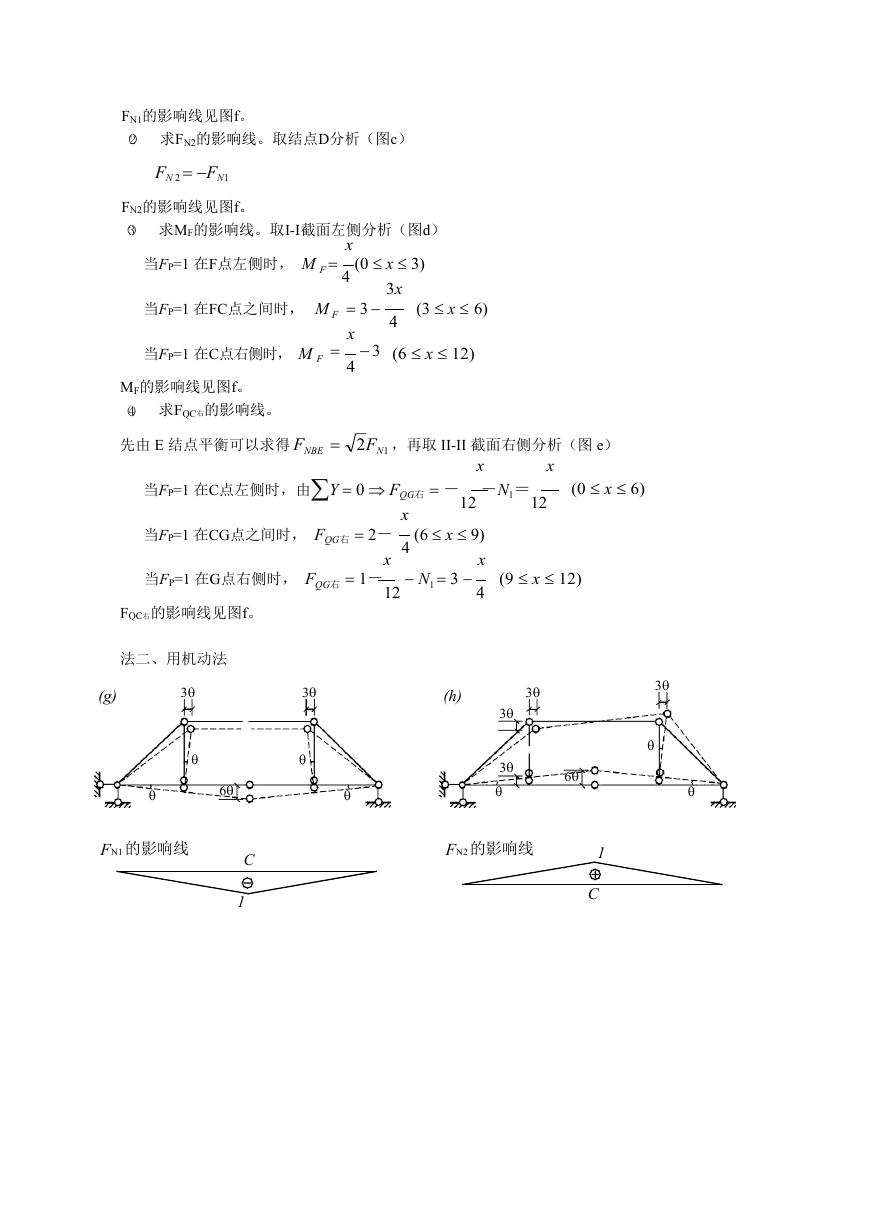
FN1的影响线见图f。（2）求FN2的影响线。取结点D分析（图c） FN 2  FN1 FN2的影响线见图f。（3）求MF的影响线。取I-I截面左侧分析（图d）当FP=1 在F点左侧时， M F  (0  x  3) 当FP=1 在FC点之间时， M F  3  当FP=1 在C点右侧时， M F   3 (3  x  6) 3x 4 (6  x  12) x 4 x 4 MF的影响线见图f。（4）求FQC右的影响线。先由 E 结点平衡可以求得 FNBE  2FN1 ，再取 II-II 截面右侧分析（图 e）当FP=1 在C点左侧时，由Y  0  FQG右  －当FP=1 在CG点之间时， FQG右  2－ x 当FP=1 在G点右侧时， FQG右  1－ 12 FQC右的影响线见图f。法二、用机动法 (g)        FN1 的影响线 C 1 x x －N1＝ (0  x  6) 12 x 4  N1  3  12 (6  x  9) x 4 (9  x  12) (h)     FN2 的影响线     1 C

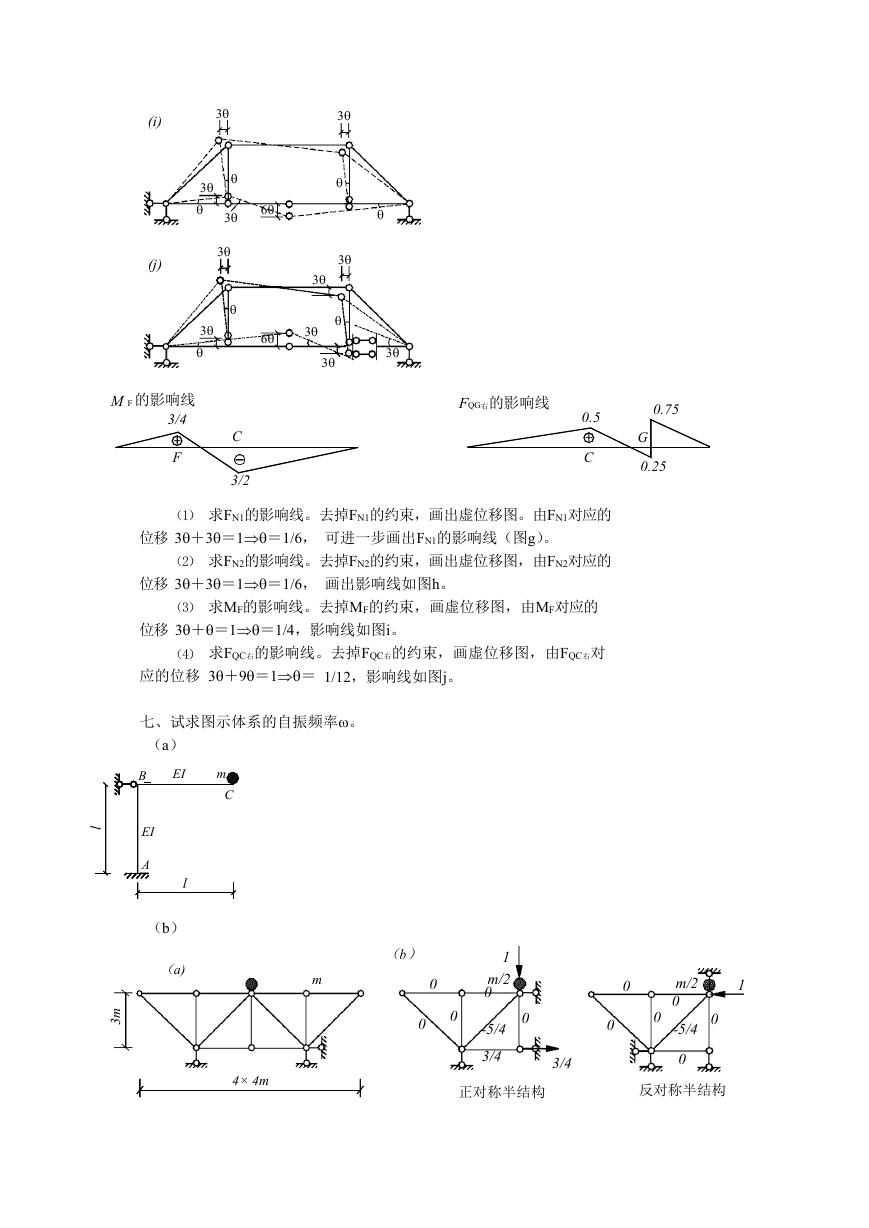
(i) (j)                     M F 的影响线 3/4 F C 3/2 FQG右的影响线 0.5 C 0.75 G 0.25 （1）求FN1的影响线。去掉FN1的约束，画出虚位移图。由FN1对应的位移 3＋3＝1＝1/6，可进一步画出FN1的影响线（图g）。（2）求FN2的影响线。去掉FN2的约束，画出虚位移图，由FN2对应的位移 3＋3＝1＝1/6，画出影响线如图h。（3）求MF的影响线。去掉MF的约束，画虚位移图，由MF对应的位移 3＋＝1＝1/4，影响线如图i。（4）求FQC右的影响线。去掉FQC右的约束，画虚位移图，由FQC右对应的位移 3＋9＝1＝ 1/12，影响线如图j。七、试求图示体系的自振频率。（a） EI B m C EI A l （b）（a) l m 3 m （b） 0 0 0 1 m/2 0 -5/4 3/4 0 0 0 1 0 0 m/2 0 -5/4 0 3/4 正对称半结构反对称半结构 4× 4m

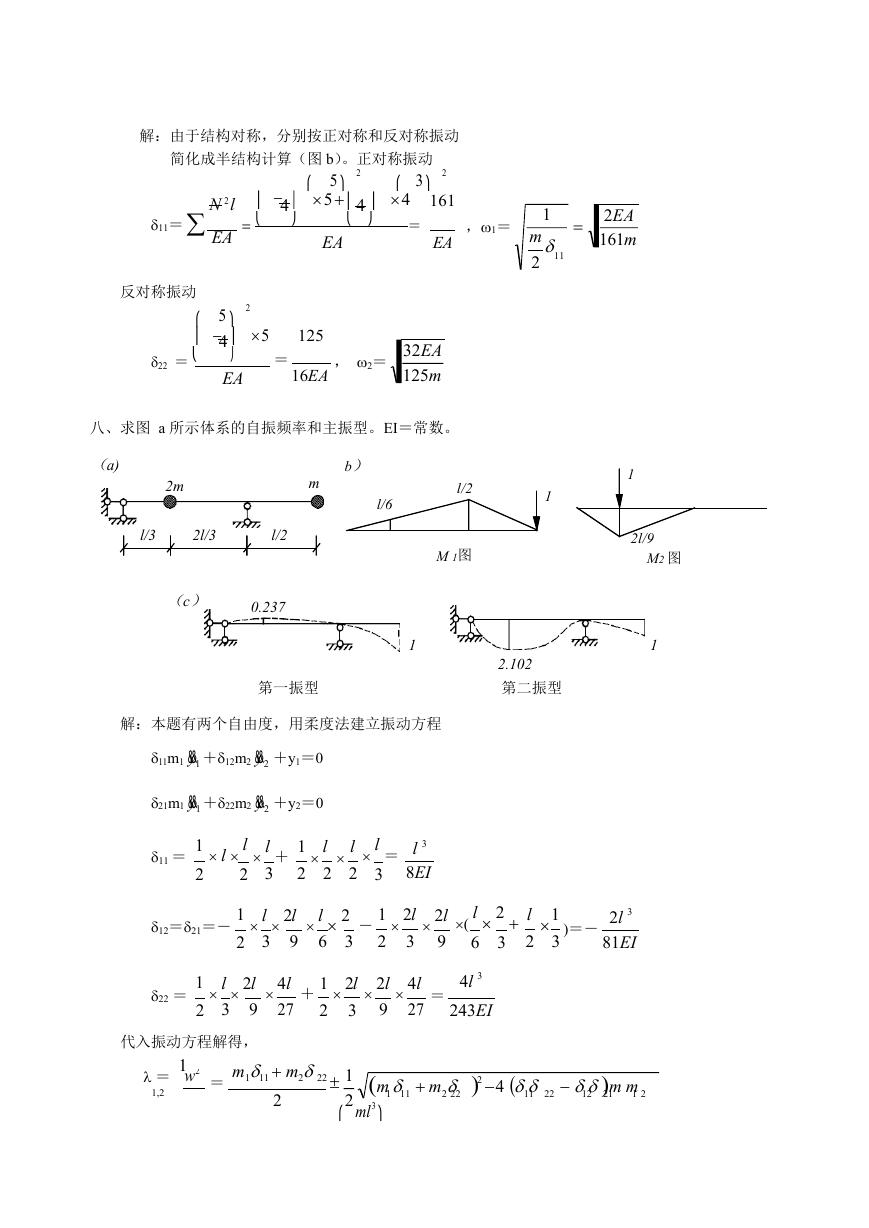
解：由于结构对称，分别按正对称和反对称振动简化成半结构计算（图 b）。正对称振动 ⎛ 3⎞ ⎟ 4 ⎠ ⎜  ⎟ 4  ⎝ ⎠ 4 ＝ ⎛ 2 N l 2 11＝ EA 5⎞ 5⎜ ⎝ EA 2 161 EA ，1＝  2EA 161m 1 m 2 11 反对称振动 2 ⎛ ⎜  ⎟ 5 22 ＝⎝ 5⎞ 4 ⎠ EA 125 ＝ 16EA ， 2＝ 32EA 125m 1 2l/9 M2 图 1 八、求图 a 所示体系的自振频率和主振型。EI＝常数。（a) 2m b） m l/6 l/2 1 l/3 2l/3 l/2 （c） 0.237 M 1图 1 第一振型解：本题有两个自由度，用柔度法建立振动方程 11m1 &y&1 ＋12m2 &y&2 ＋y1＝0 21m1 &y&1 ＋22m2 &y&2 ＋y2＝0 11 ＝ 1 2  l  l 2  l ＋ 1 3 2  l  l 2 2  l 3 ＝ l 3 8EI 2.102 第二振型 12＝21＝－ 1 2  l  2l 9 3  l  2 3 6 － 1  2l 3 2  2l 9 ( l  2  3 6 l 1 2 3 )＝－ 2l 3 81EI 22 ＝ 1 2  l  2l 9 3  4l 27 ＋ 1  2l 3 2  2l 9  4l 27 ＝ 4l 3 243EI 代入振动方程解得， 1 w2 ＝  ＝ 1,2 m111  m222  m  m   42 1 11 2 22 11 22  m m 12 21 1 2 2 1 2 ⎛ 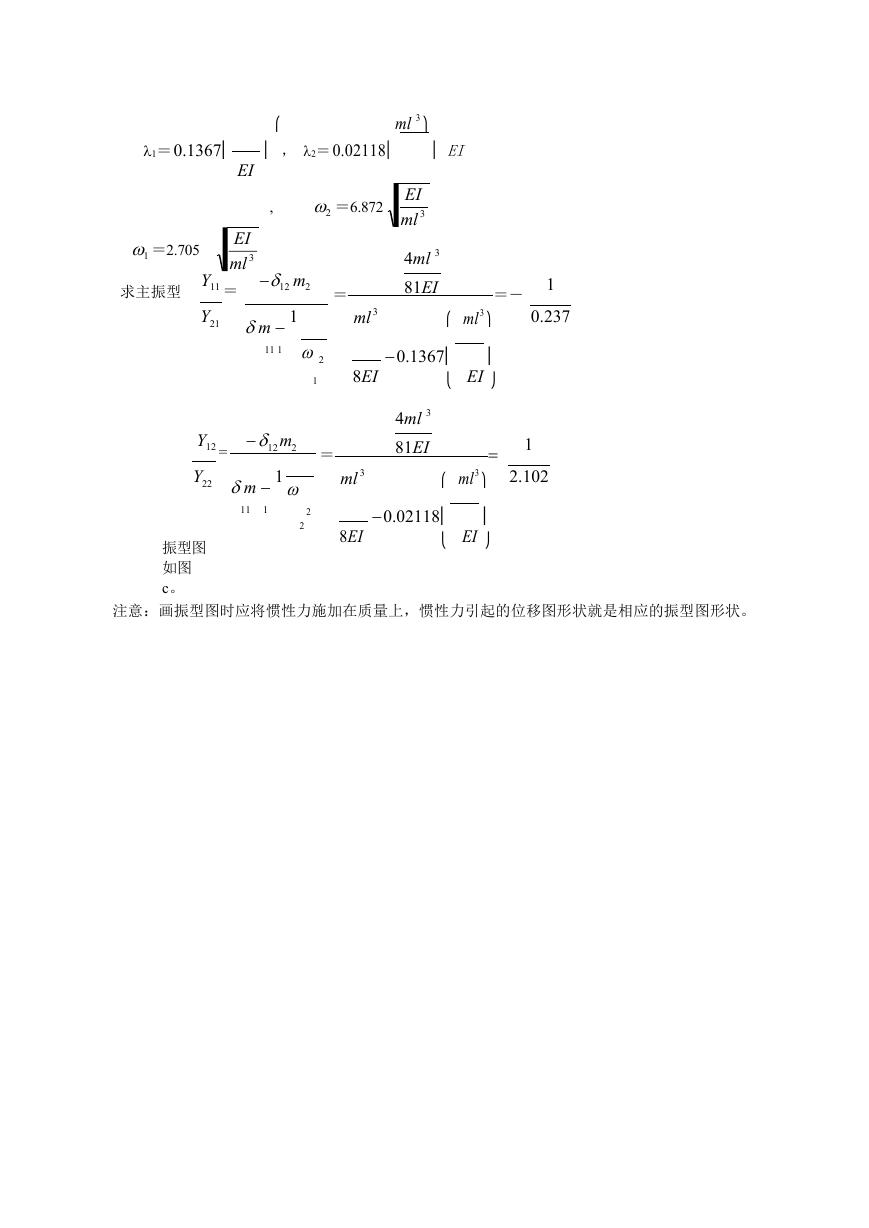ml3⎞

1＝0.1367⎜ EI 1 ＝2.705 求主振型 EI ml 3 ⎛ ⎟ ， 2＝0.02118⎜ ⎝ , 2 ＝6.872 ⎠ ml 3⎞ ⎟ EI EI ml 3 ⎝ 4ml 3 81EI ⎠ 12 m2 ＝ Y11 ＝ Y21 m  1 11 1 2  1 12m2 ＝ Y12 = Y22 m  1 ml 3 8EI 0.1367⎜ ⎛ ml3⎞ ⎟ ⎝ EI ⎠ 4ml 3 81EI ＝－ 1 0.237  1 2.102  2 2 ml 3 8EI 0.02118⎜ ⎛ ml3⎞ ⎟ ⎝ EI ⎠ 11 1 振型图如图 c。注意：画振型图时应将惯性力施加在质量上，惯性力引起的位移图形状就是相应的振型图形状。

分享到：

赞收藏

资料库

2006年山东青岛建筑工程学院结构力学考研真题.doc

相关推荐

考研

热门标签

最新资料