60°坐标系下三电平逆变器SVPWM方法的研究.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.41M 资料格式：pdf 举报版权申诉

xuhua0127-3125278-16359647574438983570.pdf-第1页.png

第1页 / 共7页

xuhua0127-3125278-16359647574438983570.pdf-第2页.png

第2页 / 共7页

xuhua0127-3125278-16359647574438983570.pdf-第3页.png

第3页 / 共7页

xuhua0127-3125278-16359647574438983570.pdf-第4页.png

第4页 / 共7页

xuhua0127-3125278-16359647574438983570.pdf-第5页.png

第5页 / 共7页

xuhua0127-3125278-16359647574438983570.pdf-第6页.png

第6页 / 共7页

xuhua0127-3125278-16359647574438983570.pdf-第7页.png

第7页 / 共7页

Tab. 2 Neutral-point current for different voltage vectors

第 28 卷第 24 期中国电机工程学报 2008 年 8 月 25 日 Proceedings of the CSEE ©2008 Chin.Soc.for Elec.Eng. 39 Vol.28 No.24 Aug.25, 2008 文章编号：0258-8013 (2008) 24-0039-07 中图分类号：TM 46 文献标识码：A 学科分类号：470⋅40 60°坐标系下三电平逆变器 SVPWM 方法的研究赵辉，李瑞，王红君，岳有军 (天津市复杂系统控制理论及应用重点实验室(天津理工大学)，天津市南开区 300191) Study on SVPWM Method Based on 60° Coordinate System for Three-level Inverter ZHAO Hui，LI Rui，WANG Hong-jun，YUE You-jun (Tianjin Key Laboratory for Control Theory & Applications in Complicated Systems (Tianjin University of Technology), Nankai District, Tianjin 300191, China) ABSTRACT: The shortcomings of traditional space vector pulse width modulation (SVPWM) method for the three-level inverter are: needing to estimate the sectors and calculating a lot of trigonometric functions, and it results in the increase of the calculating quantity of micro-processor. To solve these problems, a new method for SVPWM based on 60° coordinate system is presented in this paper. The method makes use of seven-vectors modulation where positive (or negative) small vectors are used as first vector to generate SVPWM waves. Considering the different effect of the positive and negative small vectors on capacitance, the method adjusts the working time of positive and negative small vectors by changing the voltage adjusting coefficient according to direction of load current and voltage value of capacitance C1 and C2, and this leads to reducing unbalance level of neutral-point voltage between capacitances. The results of simulation show that the new method proposed can omit the judging process of the sectors, reduce the calculating burden, and maintain the approximate balance of neutral-point voltage between capacitances. KEY WORDS: three-level inverter; 60° coordinate system; space vector pulse width modulation; balance of neutral-point voltage between capacitances 摘要：对于中点箝位三电平逆变器，传统的空间矢量脉宽调制方法需要进行大量的三角函数运算及扇区判定，增大了控制器的计算工作量。为解决这一问题，该文研究一种基于 60°坐标系的空间矢量脉宽调制方法。该方法采用正(负)小矢量首发的七段式调制技术生成所需的空间矢量脉宽调制 (space vector pulse width modulation，SVPWM)波形，同时，根据负载电流方向及上、下电容(C1、C2)电压的大小，利用正、负小矢量对电容中点电压的不同作用，通过改变电压调基金项目：天津市自然科学基金重点项目(08JCZDJC18600)；天津市科技计划项目(07ZHRDCG04500)；天津市高等学校科技发展基金项目 (2006ZD32)。整系数对正、负小矢量的作用时间进行调整，进而降低电容中点电压的不平衡程度。仿真结果表明，该方法可省去扇区判断过程，缩小计算工作量，维持电容中点电压基本平衡。关键词：三电平逆变器；60°坐标系；空间矢量脉宽调制；电容中点电压平衡 0 引言近年来，在大容量变换器中，相比于两电平逆变器，二极管箝位三电平逆变器以其输出电压更接近正弦波、电压变化率du/dt小、开关频率低、损耗小、效率高等特点，受到人们的广泛关注[1]。三电平逆变器的输出性能主要取决于调制算法， SVPWM技术以其易于数字实现，电压利用率高等特点，在三电平逆变器中得到广泛应用[2-3]。在两电平逆变器空间矢量控制的基础上提出的传统三电平逆变器的SVPWM算法[4-7]，在进行参考矢量扇区判断及计算基本矢量作用时间方面，要涉及较多的三角函数运算和表格查询，这些操作给控制器带来了很大负担。本文研究一种基于 60°坐标系的 SVPWM 算法，该算法可省去传统 SVPWM 算法中扇区判定过程及大量的三角函数运算，简化了计算。同时，根据负载电流方向及上下电容的电压，通过调节正、负小矢量作用时间，保持电容中点电压的平衡。 1 二极管箝位三电平逆变器的主电路二极管箝位三电平逆变器主电路[8]如图 1 所示。每相桥臂输出电压有 3 个值，定义开关变量Sa、 Sb、Sc代表各相桥臂的输出状态，则各相输出电压表示为

中国电机工程学报第 28 卷 40 U DC 2 U DC 2 p C1 o C2 n IG1 IG2 io IG3 IG4 IG5 IG9 D1 IG6 D3 IG10 D5 D2 IG7 D4 IG11 D6 IG8 IG12 Ua Ub Uc npn III npo opo non β II opn ppn ppo oon I pon npp opp noo ooo ppp nnn poo onn pnn α nop IV oop nno nnp nop V pno VI pop ono pnp 图 2 三电平逆变器空间电压矢量图 Fig. 2 Space voltage vector diagram for three-level inverter 在任一个小三角形区域内有最接近的 3 个基本矢量供选择，零矢量为各个扇区所共有。 2 传统 SVPWM 算法传统SVPWM算法的基本思路是根据参考电压矢量所在扇区及小三角形区域选择其邻近的三个基本矢量，再用伏秒平衡原理计算各个基本矢量的作用时间，然后，采用七段式或五段式调制生成所需的脉宽调制(pulse width modulation，PWM)波形[9-11]。在参考电压矢量所在扇区、小三角形区域判断及基本矢量作用时间的求取上需要进行大量计算[12-13]。首先，根据参考电压矢量的幅角判断该矢量位引入于哪个扇区中，然后再根据其幅值判断位于哪一个小三角形区域。 U U 、、 r2 r1 U ⎧ ⎪⎪ U ⎨ ⎪ U ⎪⎩ U 3 个变量，分别为 r3 U = β ref U α ref U = − (3) α ref = − r1 r2 r3 U β ref U − β ref αU ref / 3 / 3 U、 β ref 式中：为参考电压矢量；压矢量在坐标系上的坐标。 -α β refU refU 为参考电 = N 参考电压矢量所在扇区为 U ) 2sgn( + U 0 U 0 U sgn( 1, ⎧ ⎨ 0, ⎩ U sgn( > < = ) r1 , i r i r i r 式中 U ) 4sgn( + ) (4) r3 r2 i = 1,2,3 。判断该矢量位于扇区中哪一个小三角形区域的规则如下： / 3) ≤ U DC / 3 ，则 U （1）规则 1。若 ref ( α U β ref 该矢量位于小三角形区域 A。 U − + U （2）规则 2。若 ref ( / 3 且 α / 3 ，则该矢量位于小三角形 + / 3) / 3) U U U β ref DC ≥ > β ref DC U ( α ref 图 1 二极管箝位三电平逆变器主电路 Fig. 1 Main circuit for diode-clamped three-level inverter = S a ⎧ U ⎪ a ⎪ ⎪ U ⎨ ⎪ ⎪ U S ⎪⎩ c = = S b b c ⋅ ⋅ ⋅ U DC 2 U DC 2 U DC 2 (1) 式中：Ua、Ub、Uc分别为各相输出电压；UDC为直流侧电压；Sx=1 表示每相桥臂上面 2 的功率器件导通， Sx=0 表示每相桥臂上面 2 的功率器件导通，Sx= −1 表示每相桥臂上面 2 的功率器件导通，x为a、b、c。为表示方便，每相桥臂上面 2 个功率器件(IG1、 IG2 或 IG5、IG6 或 IG9、IG10 导通)导通时的状态用 p 表示；每相桥臂中间 2 个功率器件(IG2、IG3 或 IG6、IG7 或 IG10、IG11 导通)导通时的状态用 o 表示；每相桥臂下面 2 个功率器件(IG3、IG4 或 IG7、 IG8 或 IG11、IG12 导通)导通时的状态用 n 表示。因此，三电平逆变器可输出 33=27 种电压状态组合，对应 27 组不同的开关状态。此时，定义电压空间矢量为 U K U U U c )U K 2 α α U S b S c S a DC = + + = + + = ( ) ( ) ( ⋅ b a U [(2 S a DC − − S c ) + j 3( S b − S c )] (2) = 。在 α-β 坐标系中，三电平逆变器 27 式中组开关状态所对应的空间矢量图如图 2 所示。图 2 中各种组合(如：nno)的左起第 1 个元素代表 a 相的开关状态；第 2 个元素代表 b 相的开关状态；第 3 个元素代表 c 相的开关状态。图 2 给出了各开关状态组合与空间电压矢量的对应关系。27 组开关状态对应了 19 个空间电压矢量，称之为基本矢量。按基本矢量幅值的不同，可将其分为 4 类：大矢量、中矢量、小矢量和零矢量。除零矢量外，其余的 18 个基本矢量将圆周分为 6 个大的扇区，每个扇区又划分为 6 个小三角形区域， 1 3 S b 1 6 2j π 3eα

赵辉等： 60°坐标系下三电平逆变器 SVPWM 方法的研究 41 第 24 期区域 B。 / / > U DC / 3) U β ref U> βU （3）规则 3。若 ref 3 DC U αU U ( 3；② ref ( + − α ref ref 则该矢量位于小三角形区域 C。 βU U≤ （4）规则 4。若 ref 3 DC U U U ( 3；② ref ( − + β α α ref ref 则该矢量位于小三角形区域 D。 / 3) U β ref U > DC / / β 6 且满足：① 。 / 3) /3 U DC < 6 且满足：① 。 / /3 U < 3) DC 通过上述方法，可确定参考电压矢量所在扇区和小三角形区域。以扇区I为例，扇区I的矢量图如图 3 所示，其中T 1 、T 2 、T 3 分别为矢量作用时间。 β T1 ppn α-β坐标系中α轴重合，逆时针旋转 60°作为 h 轴。在α-β坐标系中的坐标为设参考电压矢量 ,αU ( ， ref 可知，2 坐标系间的变换为，在 g-h 坐标系下的坐标为 U U ) ( h r ref )βU refU ,g r U ⎡ ⎢ U ⎣ g r h r ⎤ ⎥ ⎦ = ⎡ 1 −⎢ ⎢ ⎢ ⎢ ⎣ 0 1 3 2 3 ⎤ ⎥ ⎥ ⎥ ⎥ ⎦ U ⎡ ⎢ U ⎣ α r ef β ref ⎤ ⎥ ⎦ (5) 由Park 变换和式(3)可知，三相静止坐标系a-b-c 与 g-h 坐标系间的变换为 g r U ′ ⎤ ⎡ a 1 0 ⎤ ⎢ ⎥′ U ⎥ ⎢ ⎥ b 1 − ⎦ ⎥′ ⎢ U ⎣ ⎦ c 式中 aU ′ 、 bU ′ 、 cU ′ 为三相输入电压。 1 −⎡ ⎢ 0 1 ⎣ U ⎡ ⎢ U ⎣ 2 3 ⎤ ⎥ ⎦ = h r (6) T2 D ppo oon C C2 A2 A1 A C1 θ T3 pon refU ooo nnn ppp T3 B T2 poo onn T1 pnn 图 3 扇区 I 中的矢量合成 Fig. 3 Vector synthesization in vector I 将三电平逆变器的 19 个基本矢量变换到 g-h 坐标系下，可得到 60°坐标系下三电平逆变器的空间矢量图，如图 4 所示。 (−2, 2) (−1, 2) 60° h (0, 2) α 确定了参考矢量所在的扇区与小三角形区域之后，便可确定与其最接近的 3 个基本矢量，然后利用伏秒平衡原理计算各基本矢量的作用时间。以扇区 I 为例，可得到各个小三角形区域的基本矢量的作用时间，如表 1 所示。表 1 扇区 I 中各基本矢量的作用时间 Tab. 1 Working time of basic vectors in sector I 区域 T1 T2 T3 A(A1,A2) 2TSMsin(π/3−θ) 2TSMsin(θ) TS[1−2Msin(π/3+θ)] B 2TS[1−Msin(π/3+θ)] TS [2Msin(π/3−θ)−1] 2TSMsin(θ) C(C1,C2) D TS[1−2Msin(θ)] TS[1−2Msin(π/3−θ)] TS [2Msin(π/3+θ)−1] TS[2Msin(θ)−1] 2TS [1−Msin(π/3+θ)] 2TSMsin(π/3−θ) refU 与α轴间的夹角；T s 为PWM 周期；注：θ为参考电压矢量为调制比。 / M = ref DC U U 3 同理，可依次计算出其它 5 个扇区中各小三角形区域基本矢量的作用时间。 3 基于 60°坐标系的 SVPWM 算法 3.1 坐标变换在α-β坐标系中，考虑到三电平基本空间矢量图为正六边形，故可采用非正交的 60°坐标系进行参考电压矢量的合成及基本矢量作用时间的计算。设采用的 60°坐标系为 g-h 坐标系，取 g 轴与 (−2, 1) (−1, 1) (0, 1) (1, 1) (−1, 0) (−2, 0) (0, 0) (1, 0) (2, 0) g (−1, −1) (0, −1) refU (1, −1) (2, −1) (0, −2) (1, −2) (2, −2) 图 4 60°坐标系下三电平逆变器的空间矢量图 Fig. 4 Space vector diagram for three-level inverter based on 60° coordinate system 3.2 确定基本矢量由图 4 可知，在 60°坐标系下所有基本矢量的坐标均为整数，故对于任意的空间参考电压矢量 refU ，距离最近的 4 个基本矢量，可由其在 60°坐标系下的坐标向上和向下取整得到。 refU 在图 4 中，参考电压矢量对应的 4 个基本矢量为 ⎧ U ⎪ ⎪ U ⎪ ⎨ U ⎪ ⎪ ⎪ U ⎩ BL LB BB LL = = = = h r g r g r U U ⎡ ⎣ U U ⎡ ⎣ h r U U ⎡ ⎣ U U ⎡ ⎣ g r g r g r h r T ⎤ ⎦ T ⎤ ⎦ T ⎤ ⎦ T ⎤ ⎦ 0 = [ [ 1 = − [ [ = − = 0 1 2 − T ] T ] 1 − T ] 1 − 2 − T ] (7)

42 中国电机工程学报第 28 卷 4 SVPWM 波形生成和电容中点电压控制 4.1 SVPWM 波形的产生确定了各基本矢量之后，为使器件开关损耗最小，每次应只有 2 个开关器件动作，且开关状态不能跳变，只能是 p ↔ o ↔ ，不能是 p ↔ n [16-18]。可通过七段式调制生成SVPWM波形[19-20]。对图 4 所示的参考电压矢量进行调制时，各开关状态的作用时序为： — nop nno refU nop nno — ，波形如图 5 所示。 nnp nnp oop — — — n refU 式中： rgU 、 rgU 分别为Urg向上和向下取整，其它同理；UBL、ULB、UBB、ULL分别为在 60°坐标系中坐标向上取整和向下取整得到的基本矢量。 UBL、ULB必为参考矢量最近的 2 个基本矢量，第 3 个最近的矢量与参考电压矢量位于对角线U BL—ULB(矢量UBL与 ULB端点的连线)的同一侧，该对角线在 60°坐标系下的方程为 refU refU g h U + = + U (8) + h BL 式中 U、 gU h BL BL 根据表达式 g BL 分别为U BL在g、h轴上的投影。 U U U ( − refU 的符号，可确定第 3 个距离参考矢量最近的基本矢量。当表达式的值大于 0 时，UBB为第 3 个最近的基本矢量，当表达式的值小于 0 时，ULL为第 3 个最近的基本矢量。图 2 所示参考电压矢量的 3 个最近的基 U h BL g BL − ) g r h r 本矢量为： 0 2 − ⎤ ⎡ , ⎥ ⎢ ⎦ ⎣ 1 − ⎤ ⎡ , ⎥ ⎢ 1 − ⎦ ⎣ 0 ⎤ ⎥ 1 − ⎦ ⎡ ⎢ ⎣ 。从图 2、4 可知，由对应的基本矢量确定各功率器件的开关状态。选择具体的开关状态，特别是选择小矢量时，要根据此时电容电流的流进或流出来选择，以保持电容中点电压的平衡[14-15]。 3.3 各基本矢量作用时间的计算确定了参考电压矢量的 3 个最近的基本矢量 U 2 + d 3 ⋅ U 3 (9) 后，根据伏秒平衡原理可列出 ⋅ + d 2 U T ⎧ ⋅ ⎪ S ref ⎨ d d + ⎪⎩ 2 1 U U = 1 BL U d ⋅ = 1 1 d T + = S 3 U U = U U B B = 3 2 LB ；；式中：或；为 PWM周期；d1、d2、d3为电压U1、U2、U3的作用时间。所有开关状态的坐标均为整数，方程组(9)的解可基于参考电压矢量的小数部分获得。 LLU sT B=U U B 3 时，将方程组在 g-h 坐标下展开，当解得同理，当 ⎧ ⎪ ⎨ ⎪ ⎩ d 1 d 2 d 3 d BL d LB d BB U ( = − g r U ( = − g r T d − = S 1 = = = L=U U 时，可得 L 3 d = − ⎧ BL ⎪ d = − ⎨ LB ⎪ d d = ⎩ LL 1 U ( g r U ( T S d 1 d 2 d 3 = = = g r − U − h BB U − g BB d − 2 ) ) U g LL U h BB d − 2 ) ) T ⋅ s T ⋅ s (10) T ⋅ s T ⋅ s (11) 计算表明，在 60°坐标系下，可省去扇区判断过程，并避免进行大量的三角函数运算，使计算工作量大大缩小。 — 态状 U a 态状 b U 态状 U c p o n p o n p o n Ts Ts Ts t d 2 2 kd 3 2 d 1 2 (1 − (1 k d ) 3 2 − k d ) 3 2 d 1 2 d 2 2 kd 3 2 图 5 SVPWM 波形 Fig. 5 SVPWM waveform 4.2 电容中点电压控制分析图 1 所示主电路可知：电容中点电位不平衡程度是由电容中点电流io和直流侧电容的大小决定的，电容中点电位的变化率为 U Δ np = ，由此 i o C 2 得到电容中点电流与各个电压矢量状态的关系，如表 2 所示。表 2 中点电流和电压矢量的对应关系 Tab. 2 Neutral-point current for different voltage vectors io ib ia ic ib ia ic io ia ib ic ic ia ib io −ic −ia −ib −ia −ib −ic 正小矢量负小矢量中矢量 pon opn npo nop onp pno ppo opp pop poo opo oop onn non nno oon noo ono 注：三相电流ia 、ib 、ic的电流方向以从电容中点流出的方向为正。零矢量和大矢量对电容中点电压(电流)无影响；正负小矢量对电容中点电压产生的影响是相反的；而中矢量对电容中点电压的影响是不可直接控制的[21]。可通过调节正负矢量相对作用时间(总的作用时间不变)来对由中矢量引起的电容中点电压的

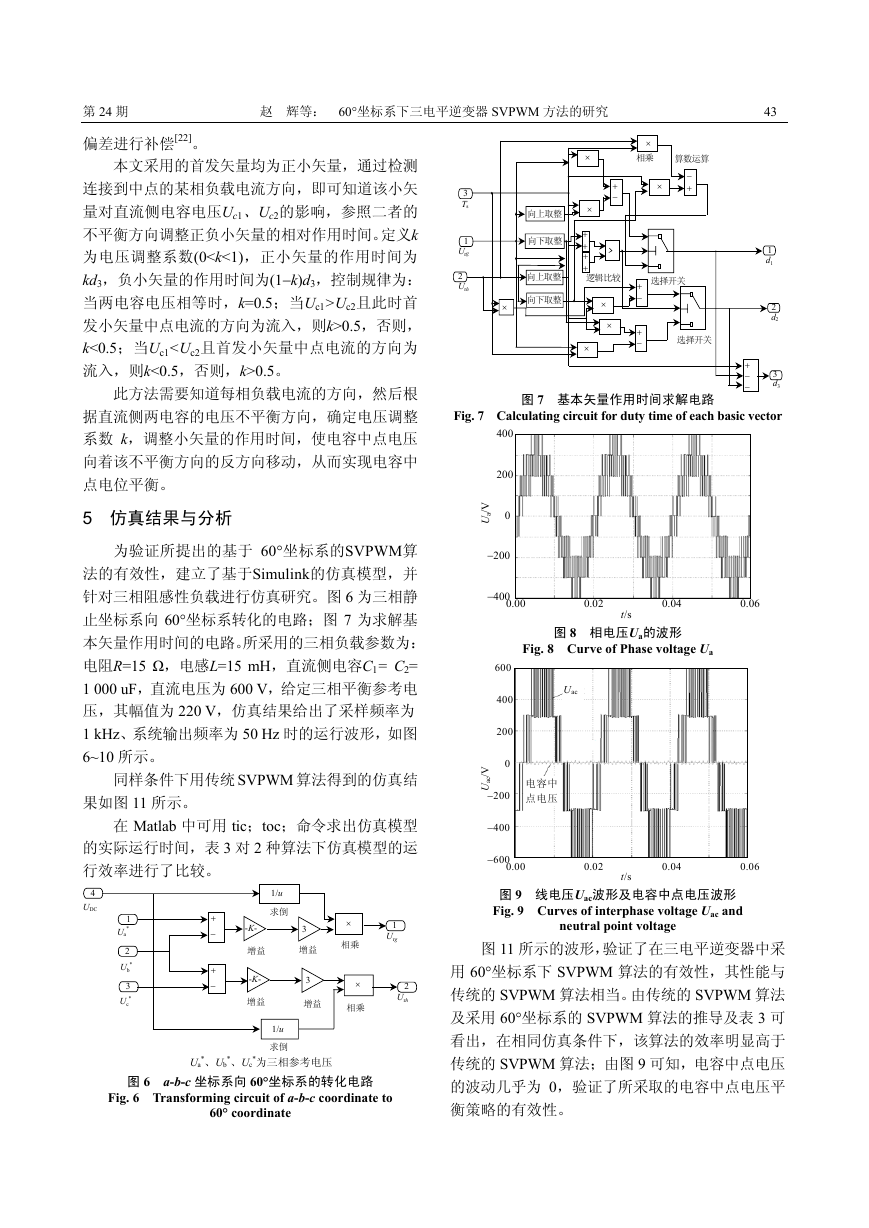
第 24 期赵辉等： 60°坐标系下三电平逆变器 SVPWM 方法的研究 43 偏差进行补偿[22]。本文采用的首发矢量均为正小矢量，通过检测连接到中点的某相负载电流方向，即可知道该小矢量对直流侧电容电压Uc1、Uc2的影响，参照二者的不平衡方向调整正负小矢量的相对作用时间。定义k 为电压调整系数(0Uc2且此时首发小矢量中点电流的方向为流入，则k>0.5，否则， k<0.5；当Uc10.5。此方法需要知道每相负载电流的方向，然后根据直流侧两电容的电压不平衡方向，确定电压调整系数 k，调整小矢量的作用时间，使电容中点电压向着该不平衡方向的反方向移动，从而实现电容中点电位平衡。 5 仿真结果与分析为验证所提出的基于 60°坐标系的SVPWM算法的有效性，建立了基于Simulink的仿真模型，并针对三相阻感性负载进行仿真研究。图 6 为三相静止坐标系向 60°坐标系转化的电路；图 7 为求解基本矢量作用时间的电路。所采用的三相负载参数为：电阻R=15 Ω，电感L=15 mH，直流侧电容C1= C2= 1 000 uF，直流电压为 600 V，给定三相平衡参考电压，其幅值为 220 V，仿真结果给出了采样频率为 1 kHz、系统输出频率为 50 Hz 时的运行波形，如图 6~10 所示。同样条件下用传统 SVPWM 算法得到的仿真结果如图 11 所示。在 Matlab 中可用 tic；toc；命令求出仿真模型的实际运行时间，表 3 对 2 种算法下仿真模型的运行效率进行了比较。 4 UDC 1/u 1 * Ua + − 2 * Ub 3 * Uc + − 3 增益 3 增益 × 相乘 1 Urg × 相乘 2 Urh 求倒 -K- 增益 -K- 增益 1/u 求倒 Ua *、Ub *、Uc *为三相参考电压图 6 a-b-c 坐标系向 60°坐标系的转化电路 Fig. 6 Transforming circuit of a-b-c coordinate to 60° coordinate 3 Ts 1 Urg 2 Urh 向上取整向下取整向上取整向下取整 × × 相乘算数运算 × − + 选择开关选择开关 + − + − × × + − + + + + 逻辑比较 × × × 1 d1 2 d2 + − − 3 d3 图 7 基本矢量作用时间求解电路 Fig. 7 Calculating circuit for duty time of each basic vector 400 200 V / a U 0 −200 0.06 −400 0.00 0.02 t/s 0.04 图 8 相电压U a的波形 Fig. 8 Curve of Phase voltage Ua Uac 电容中点电压 600 400 200 0 V / c a U −200 −400 −600 0.00 0.02 t/s 0.04 0.06 图 9 线电压U ac波形及电容中点电压波形 Fig. 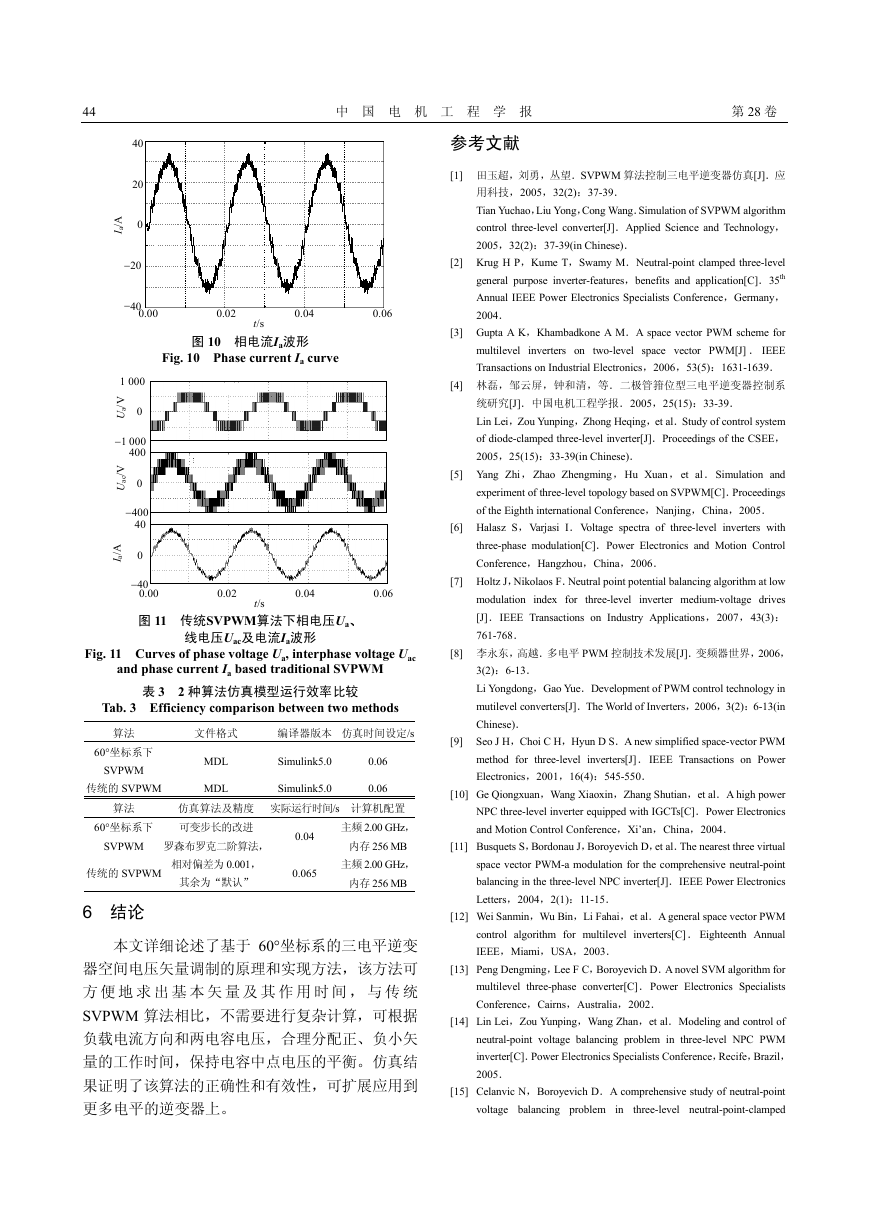9 Curves of interphase voltage Uac and neutral point voltage 图 11 所示的波形，验证了在三电平逆变器中采用 60°坐标系下 SVPWM 算法的有效性，其性能与传统的 SVPWM 算法相当。由传统的 SVPWM 算法及采用 60°坐标系的 SVPWM 算法的推导及表 3 可看出，在相同仿真条件下，该算法的效率明显高于传统的 SVPWM 算法；由图 9 可知，电容中点电压的波动几乎为 0，验证了所采取的电容中点电压平衡策略的有效性。

44 40 20 A / a I 0 −20 −40 0.00 1 000 V / a U 0 −1 000 400 V / c a U 0 −400 40 A / a I 0 0.02 t/s 0.04 图 10 相电流I a波形 Fig. 10 Phase current Ia curve 0.06 −40 0.00 0.02 t/s 0.04 图 11 传统SVPWM 算法下相电压Ua、线电压Uac及电流Ia波形 0.06 Fig. 11 Curves of phase voltage Ua, interphase voltage Uac and phase current Ia based traditional SVPWM 表 3 2 种算法仿真模型运行效率比较 Tab. 3 Efficiency comparison between two methods 算法 60°坐标系下 SVPWM 传统的 SVPWM 文件格式 MDL MDL 编译器版本仿真时间设定/s Simulink5.0 Simulink5.0 0.06 0.06 仿真算法及精度实际运行时间/s 计算机配置可变步长的改进主频 2.00 GHz，算法 60°坐标系下 SVPWM 罗森布罗克二阶算法，传统的 SVPWM 相对偏差为 0.001，其余为“默认” 6 结论 0.04 内存 256 MB 0.065 主频 2.00 GHz，内存 256 MB 本文详细论述了基于 60°坐标系的三电平逆变器空间电压矢量调制的原理和实现方法，该方法可方便地求出基本矢量及其作用时间，与传统 SVPWM 算法相比，不需要进行复杂计算，可根据负载电流方向和两电容电压，合理分配正、负小矢量的工作时间，保持电容中点电压的平衡。仿真结果证明了该算法的正确性和有效性，可扩展应用到更多电平的逆变器上。中国电机工程学报第 28 卷参考文献 [1] 田玉超，刘勇，丛望．SVPWM 算法控制三电平逆变器仿真[J]．应用科技，2005，32(2)：37-39． Tian Yuchao，Liu Yong，Cong Wang．Simulation of SVPWM algorithm control three-level converter[J]．Applied Science and Technology， 2005，32(2)：37-39(in Chinese)． [2] Krug H P，Kume T，Swamy M．Neutral-point clamped three-level general purpose inverter-features，benefits and application[C]．35th Annual IEEE Power Electronics Specialists Conference，Germany， 2004． [3] Gupta A K，Khambadkone A M．A space vector PWM scheme for multilevel inverters on two-level space vector PWM[J] ． IEEE Transactions on Industrial Electronics，2006，53(5)：1631-1639． [4] 林磊，邹云屏，钟和清，等．二极管箝位型三电平逆变器控制系统研究[J]．中国电机工程学报．2005，25(15)：33-39． Lin Lei，Zou Yunping，Zhong Heqing，et al．Study of control system of diode-clamped three-level inverter[J]．Proceedings of the CSEE， 2005，25(15)：33-39(in Chinese)． [5] Yang Zhi，Zhao Zhengming，Hu Xuan，et al．Simulation and experiment of three-level topology based on SVPWM[C]．Proceedings of the Eighth international Conference，Nanjing，China，2005． [6] Halasz S，Varjasi I．Voltage spectra of three-level inverters with three-phase modulation[C]．Power Electronics and Motion Control Conference，Hangzhou，China，2006． [7] Holtz J，Nikolaos F．Neutral point potential balancing algorithm at low modulation index for three-level inverter medium-voltage drives [J]．IEEE Transactions on Industry Applications，2007，43(3)： 761-768． [8] 李永东，高越．多电平 PWM 控制技术发展[J]．变频器世界，2006， 3(2)：6-13． Li Yongdong，Gao Yue．Development of PWM control technology in mutilevel converters[J]．The World of Inverters，2006，3(2)：6-13(in Chinese)． [9] Seo J H，Choi C H，Hyun D S．A new simplified space-vector PWM method for three-level inverters[J]．IEEE Transactions on Power Electronics，2001，16(4)：545-550． [10] Ge Qiongxuan，Wang Xiaoxin，Zhang Shutian，et al．A high power NPC three-level inverter equipped with IGCTs[C]．Power Electronics and Motion Control Conference，Xi’an，China，2004． [11] Busquets S，Bordonau J，Boroyevich D，et al．The nearest three virtual space vector PWM-a modulation for the comprehensive neutral-point balancing in the three-level NPC inverter[J]．IEEE Power Electronics Letters，2004，2(1)：11-15． [12] Wei Sanmin，Wu Bin，Li Fahai，et al．A general space vector PWM control algorithm for multilevel inverters[C] ． Eighteenth Annual IEEE，Miami，USA，2003． [13] Peng Dengming，Lee F C，Boroyevich D．A novel SVM algorithm for multilevel three-phase converter[C]．Power Electronics Specialists Conference，Cairns，Australia，2002． [14] Lin Lei，Zou Yunping，Wang Zhan，et al．Modeling and control of neutral-point voltage balancing problem in three-level NPC PWM inverter[C]．Power Electronics Specialists Conference，Recife，Brazil， 2005． [15] Celanvic N，Boroyevich D．A comprehensive study of neutral-point three-level neutral-point-clamped voltage balancing problem in

第 24 期赵辉等： 60°坐标系下三电平逆变器 SVPWM 方法的研究 45 voltage PWM inverters[J]．IEEE Transactions on Power Electronics， 2000，15(3)：242-249． [16] 姜旭，肖湘宁，任爱平，等．改进的多电平SVPWM及其广义算法研究[J]．中国电机工程学报，2007，27(4)：84-89． Jiang Xu，Xiao Xiangning，Ren Aiping，et al．An improved multilevel SVPWM and its generalized algorithm[J]．Proceedings of the CSEE， 2007，27(4)：84-89(in Chinese)． [17] 宋文详，陈国呈．三电平中点箝位式逆变器 SVPWM 方法的研究 [J]．电工电能新技术，2004，23(4)：30-33． Song Wenxiang，Chen Guocheng．Study on SVPWM method for three-level neutral-point-clamped(NPC) in inverter[J] ． Advanced Technology of Electrical Engineering and Energy，2004，23(4)： 30-33(in Chinese)． [18] Kaku B，Miyashita I，Sone S．Switching loss minimized space vector PWM method for IGBT inverter[J]．IEEE Transactions on Power Applications，1997，144(3)：182-190． [19] 孟永庆，沈传文，刘正，等．基于零序电压注入的三电平中点箝位整流器中点电位控制方法的研究[J]．中国电机工程学报， 2007， 27(10)：92-97． Meng Yongqing，Shen Chuanwen，Liu Zheng，et al．Study on neutral-point control method for three-level NPC rectifiers by injecting zero-sequence voltage[J]．Proceedings of the CSEE，2007，27(10)： 92-97(in Chinese)． [20] 宋强，刘文华，严干贵，等．基于零序电压注入的三电平 NPC 逆变器中点电位平衡控制方法[J]．中国电机工程学报，2004，25(5)： 57-62． Song Qiang，Liu Wenhua，Yan Gangui，et al． A neutral-point potential balancing algorithm for three-level NPC inverters by using analytically injected zero-sequence voltage[J]．Proceedings of the CSEE，2004， 25(5)：57-62(in Chinese)． [21] 金舜，钟彦儒，明正峰，等．一种控制中点电位并消除窄脉冲的三电平 PWM 方法[J]．中国电机工程学报，2003，23(10)：114-118． Jin Shun，Zhong Yanru，Ming Zhengfeng，et al．A three-level PWM method of neutral-point balancing and narrow-pulse elimination [J]．Proceedings of the CSEE，2003，23(10)：114-118(in Chinese)． [22] 翁海清，孙旭东，刘丛伟，等．三电平逆变器直流侧电压平衡控制方法的改进[J]．中国电机工程学报，2006，22(9)：94-97． Weng Haiqing，Sun Xudong，Liu Congwei，et al． Improvement on DC-voltage balance control method of three-level inverter[J]． Proceedings of the CSEE，2006，22(9)：94-97(in Chinese)．收稿日期：2008-01-31。作者简介：赵辉(1963—)，男，博士，教授，主要研究方向为电力电子控制技术，zhaohui3379@126.com；李瑞(1981—)，男，硕士研究生，主要研究方向为电力电子控制技术及其在风力发电系统的应用。 (编辑谷子 ) 赵辉

分享到：

赞收藏

资料库

60°坐标系下三电平逆变器SVPWM方法的研究.pdf

相关推荐

开发技术

热门标签

最新资料