第 37 卷 第 5 期 电 子 科 技 大 学 学 报 Vol.37 No.5 2008年9月 Journal of University of Electronic Science and Technology of China Sep. 2008 三阶卡尔曼滤波数字锁频环设计及性能分析 李金海，巴晓辉，陈 杰 (中国科学院微电子研究所 北京 朝阳区 100029) 【摘要】提出了一种基于三维卡尔曼滤波的三阶数字锁频环设计方法，并将该锁频环用于高动态GPS信号的载波跟踪。 推导了卡尔曼滤波与数字锁频环之间的等效关系，给出了基于该方法设计的锁频环的等效噪声带宽闭式解，分析了环路的暂 态性能和稳态性能。以暂态带宽和均方根频率跟踪误差为性能指标，对基于该方法设计的锁频环和固定增益的数字锁频环进 行了仿真对比。结果表明，在具有相同稳态带宽的情况下，两种环路具有可比拟的动态和静态跟踪误差，但基于该方法设计 的环路具有较高的初始捕获带宽，环路收敛时间大大降低。 关 键 词 锁频环; 全球定位系统; 高动态; 卡尔曼滤波 中图分类号 TN911.22 文献标识码 A Design and Performance Analysis of 3rd Order Kalman Filter Digital Frequency-Locked Loop LI Jin-hai, BA Xiao-hui, and Chen Jie (Institute of Microelectronics, Chinese Academy of Sciences Chaoyang Beijing 100029) Abstract A three-dimensional Kalman filter based digital frequency-locked loop design approach is proposed for the carrier tracking of high dynamic global positioning system signals. The equivalence between Kalman filer and digital frequency-locked loop is derived. The transient-state and steady-state loop performance are analyzed. The simulation results show that the Kalman filter based digital frequency locked loop (DFLL) has much wider bandwidth in the transient-state than the fixed-gain DFLL while both have the same steady-state bandwidth, and the convergence time decreases a lot. Key words FLL; global positioning system; high dynamic; Kalman filter 对于高动态GPS接收机，一般认为接收信号中 含有载波多普勒频移的二阶时间导数[1]，因此，最 好采用二阶以上的环路进行信号跟踪。但是相对于 了环路的收敛时间，非常适用于高动态等恶劣环境。 1 三维卡尔曼滤波的数字锁频环设计 1.1 信号模型 低阶环路，高阶环路的捕获带宽较小，环路收敛时 间相对较长。为了缩短收敛时间，必须增大环路等 效噪声带宽(以下简称带宽)，提高环路的捕获性能。 但带宽的增大，会导致稳态跟踪误差性能的恶化。 因此，设计人员希望环路在初始阶段具有较宽的带 宽，而在稳态跟踪阶段具有较小的带宽，即环路带 宽具有一定的自适应性，以便兼顾环路的捕获性能 和稳态跟踪性能。 现有文献多采用扩展卡尔曼滤波设计带宽自适 应的FLL[2-4]，且环路阶数较低，不适于高动态环境 的应用。本文提出了一种基于线性卡尔曼滤波理论 的三阶FLL设计方法，通过带宽的自适应调整降低 X k 1 + = k 1| + X + x k X [ = 建立动态载波信号模型的方法有很多，本文采 用离散化的连续域维纳过程加速度(continuous Wiener process acceleration model，CWPA)模型[5]，则有： u (1) F k k ， x 、 x 和 x x 式中 系统状态变量为 分别代表待跟踪信号的瞬时频率、频率变化率和频 k+F 和驱动噪声 ku 及其协 率加速度；状态转移矩阵 1| k 方差矩阵 kQ 分别表示为[5]： T u 1 0 (2) T 2 u T u 1 ]T x F k / 2 = e A T u 1| + k 1 0 0 ⎡ ⎢ = ⎢ ⎢ ⎣ ⎤ ⎥ ⎥ ⎥ ⎦ 收稿日期： 2007 − 03 − 31; 修回日期： 2007 − 08 − 24 基金项目：国家自然科学基金(60425413) 作者简介：李金海(1978 − )，男，博士生，主要从事卫星导航定位算法、通信系统SOC设计方面的研究. 

电 子 科 技 大 学 学 报 第 37 卷 678 Q k = E u u T k k ⎡ ⎣ ⎤ ⎦ = qT u T / 20 4 ⎡ u ⎢ T /8 3 ⎢ u ⎢ T / 6 2 ⎣ u T 3 u T 2 u T u /8 / 3 / 2 T / 6 2 u T / 2 u 1 ⎤ ⎥ ⎥ ⎥ ⎦ (3) 式中 Tu为采样周期。假设观测量 ky 为标量，代表 被噪声污染的待跟踪信号的瞬时频率，则信号动态 模型的状态方程和观测方程分别为： k k k 1| + k k | + K ka F k = , ˆ X ]T ˆ X [ =K F k k k 1| 1| + + K K K , (8) 1 − 为 k 时刻的卡尔曼增益。 式中 在实际实现过程中，观测量 ky 是无法直接得到的， 因此无法得到所需的新息，但可以通过鉴频器得到 经过模处理后的新息估计，仍记为 ka 。 0 1 2 k k k k 将 式(2)~ 式(7) 代 入 式(8) ， 并 进 行Z 变 换 可 得 X X k y F = k k 1| + H X + v k 式中 观测噪声 kv 是协方差为 声。观测矩阵为： 1 + = k + k k k u (4) k (5) vσ=R 的高斯白噪 2 k =H [ 1 0 0 ] (6) 1.2 卡尔曼滤波与数字锁频环 在建立了上述信号模型后，为利用卡尔曼滤波 理论设计数字锁频环，考虑到计算时延和环路更新 时延，需采用卡尔曼滤波的预测器形式。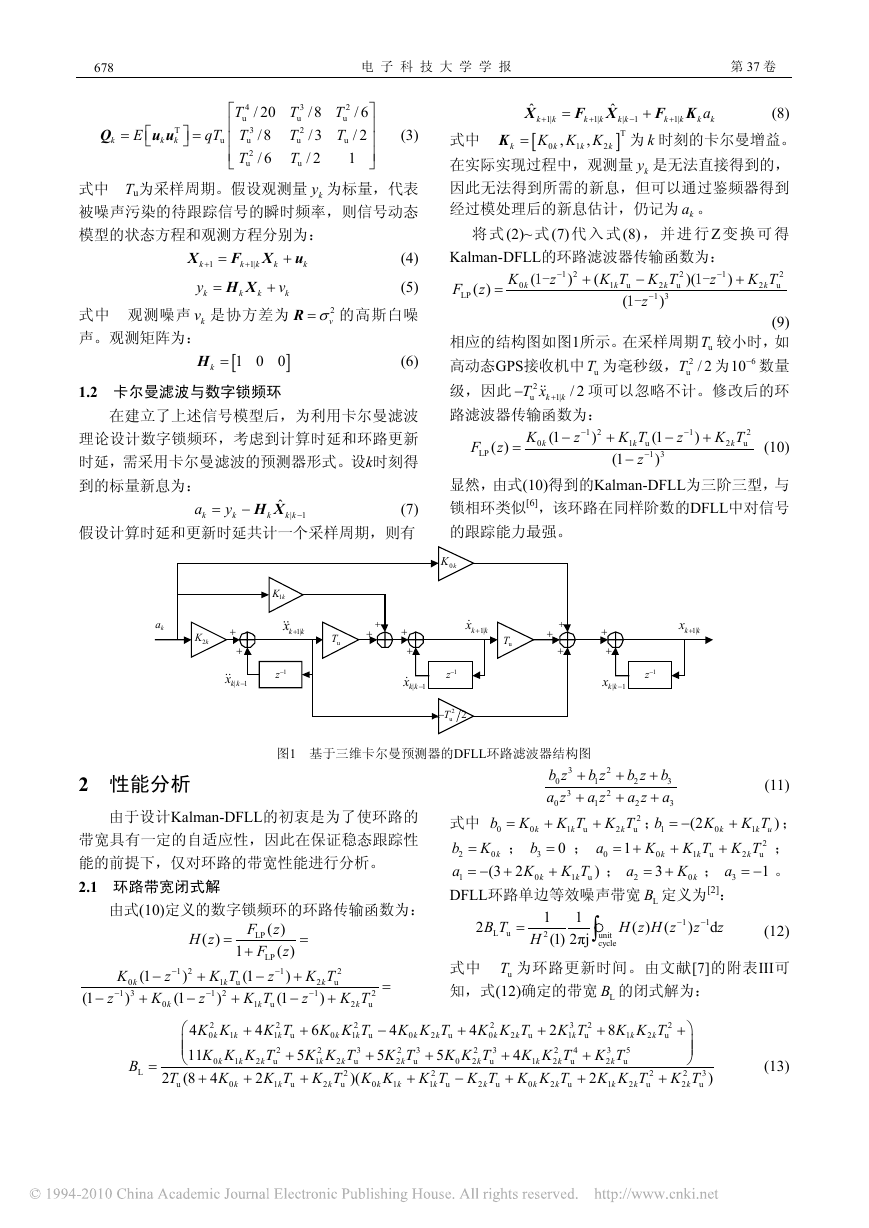设k时刻得 到的标量新息为： a k (7) 假设计算时延和更新时延共计一个采样周期，则有 ˆ − H X = y k k | 1 − k k k 2 0 ( = + + K ) 1 2 − z ( 1- z )( 1- K T 2 k u F z ( ) LP Kalman-DFLL的环路滤波器传输函数为： ) 1 − K T K T 2 − k k u 2 u 1 z ) ( 1 3 − 1- (9) 相应的结构图如图1所示。在采样周期 uT 较小时，如 高动态GPS接收机中 uT 为毫秒级， 2 T 为 610− 数量 u / 2 − T x + 级，因此 2 项可以忽略不计。修改后的环 k u 1| 路滤波器传输函数为： K T (1 ) 1 2 + k 1 u z (1 ) 1 3 − − F z ( ) LP K T 2 k u (10) / 2 (1 K − − + = z z ) − − 1 0 2 k k 显然，由式(10)得到的Kalman-DFLL为三阶三型，与 锁相环类似[6]，该环路在同样阶数的DFLL中对信号 的跟踪能力最强。 0kK 0kK 1kK ka 2kK + + k kx − | 1 kx + 1| k + + uT + + x + k k 1| uT + + + + + x + k k 1| 1z− k kx − | 1 1z− 2 2 u 2T− u 2T− 图1 基于三维卡尔曼预测器的DFLL环路滤波器结构图 1z− k kx − | 1 2 性能分析 由于设计Kalman-DFLL的初衷是为了使环路的 带宽具有一定的自适应性，因此在保证稳态跟踪性 能的前提下，仅对环路的带宽性能进行分析。 2.1 环路带宽闭式解 由式(10)定义的数字锁频环的环路传输函数为： 2 2 3 K (11) b z + 0 a z 3 + 0 K T = + k k 0 1 u b = ； 0 ； 3 K T K k 1 u b z b b z + + 2 3 1 a z a a z + + 3 2 1 K b K T K T b 式中 ) (2 2 = − + + ；1 k u k k 1 0 u 2 0 K= b K T K K T a 1 2 = + + + ； k k k 2 u 1 u 0 0 a a = − 。 K a 1 3 ) = + ； 3 = − + ； 2 1 DFLL环路单边等效噪声带宽 LB 定义为[2]： 0k (3 2 + 0 0 2 k k ； 2 B T L u = H 1 1 (1) 2πj 2 ∫ unit cycle H z H z ( ( ) − 1 ) z − 1 z d (12) K k 0 ) 1 3 − (1 + − K z 0 k (1 − z ) 1 2 − (1 − = = + z H z ( ) F z ( ) LP F z ( ) 1 + LP K T z ) (1 1 − + − k u 1 K T ) (1 1 2 − − + k u 1 K K K T 4 4 2 2 k k k u 0 1 1 K K K T 11 2 + k u 2 K T 2 + k 1 u k K + + k 1 0 k ⎛ ⎜ ⎜ ⎝ 0 T 2 (8 4 u B L = uT 为环路更新时间。由文献[7]的附表III可 2 = 式中 知，式(12)确定的带宽 LB 的闭式解为： K T 2 k u 2 z K T ) 1 2 − + k u K T K K T K K T K K T K K T 4 6 4 2 8 2 2 3 2 2 − + + k k k k k k k k 2 u u u 0 1 0 2 1 u 1 u K T K K T K K T K K T K T 5 5 5 4 3 2 2 3 3 2 4 2 5 3 + + + + k k k k k k k u 2 u 1 u 2 u 2 1 u 2 K K T K K T K T K T K T K K )( 2 2 2 2 + + + + k k k k k 1 u u u 1 u 1 u ⎞ ⎟ ⎟ ⎠ K T 3 2 k u 2 0 − + + + + 2 2 0 2 2 0 2 2 0 k k k k k (13) ) 

第5期 李金海 等: 三阶卡尔曼滤波数字锁频环设计及性能分析 679 将环路的暂态增益和稳态增益分别代入式(13)，即可 得到环路的暂态带宽和稳态带宽。 2.2 暂态性能分析 由于卡尔曼滤波的暂态过程存在不确定性，无 法给出暂态增益的理论解，因此只能通过仿真得到 暂态增益，并进而得到暂态带宽性能。 2.3 稳态性能分析 由卡尔曼滤波的滤波稳定性原理[8]可知，无论 滤波初值如何选择，当时间 k 充分大以后，卡尔曼 滤波都会达到稳态，且满足： =P lim k k →∞ Σ FPF = = P (14) T + BQB (15) T = ΣH HΣH [ T T + R ] 1 − = K (16) 1| + k P lim k k →∞ K lim k →∞ k 式中 P为正定阵，代表稳态滤波误差协方差矩阵； K 为稳态卡尔曼增益；Σ 为稳态一步预测协方差矩 阵，且矩阵 Σ 满足Riccati矩阵代数方程： T [ − Σ F Σ ΣH HΣH = 假设本系统达到稳态时矩阵 Σ 可表示为： R HΣ F ] ] − + + [ T T 1 BQB (17) T Σ 2 ⎡ σ ρ ρ 1 2 ⎢ = ⎢ ρ σ ρ 1 3 ⎢ 2 ρ ρ σ ⎣ 3 1 2 2 2 3 (18) ⎤ ⎥ ⎥ ⎥ ⎦ 则有： HΣH T + R = [ 1 0 0 2 vσ σ+ 2 1 ] 1 2 2 2 ⎡ σ ρ ρ 1 2 ⎢ ρ σ ρ ⎢ 1 3 ⎢ 2 ρ ρ σ ⎣ 3 (19) 1 ⎤ ⎡ ⎤ ⎥ ⎢ ⎥ 0 ⎥ ⎢ ⎥ ⎥ ⎢ ⎥⎣ ⎦ 0 ⎦ 2 σ v + = 2 3 将式(19)代入式(16)可得到稳态卡尔曼增益为： ] T K ΣH HΣH [ σ ρ ρ 2 R ] − = + = 2 1 [ T T 1 1 1 + 2 σ σ v 2 1 (20) 因此，为得到Kalman-DFLL稳态带宽的理论解，只 需求解Riccati矩阵代数式(17)方程，得到稳态一步预 测误差矩阵 Σ ，并将结果依次代入式(20)和式(13) 即可。 由式(17)表示的Riccati矩阵代数方程的求解方 法很多，但对于二维以上的非时变系统，仅能得到 数值解[9]，借助文献[9-10]给出的基于特征值、特征 向量的求解方法可以方便的求得本系统的 Σ 矩阵。 将上述Kalman-DFLL用于高动态GPS载波跟踪 − ， 。将上述参数分别代入式 T 的环路设计，各系统参数为：采样周期 u q = eσ= 1 1000 e= 2 ， R = − 3 1 2 v (2)、式(3)、式(6)、式(13)、式(17)、式(20)，可得到 系统稳态带宽为： B = L 10.493 801891308 71 (21) 至此，完成了对Kalman-DFLL环路稳态带宽性能的 分析。 3 仿真结果 为验证上述理论推导的正确性，采用文献[1]中 规定的高动态GPS信号进行仿真，以暂态带宽和稳 态信号跟踪的RMS频率误差为性能指标，对稳态带 宽为10.49 Hz的Kalman-DFLL和 具 有同样 带宽 的 F-DFLL进行了性能对比。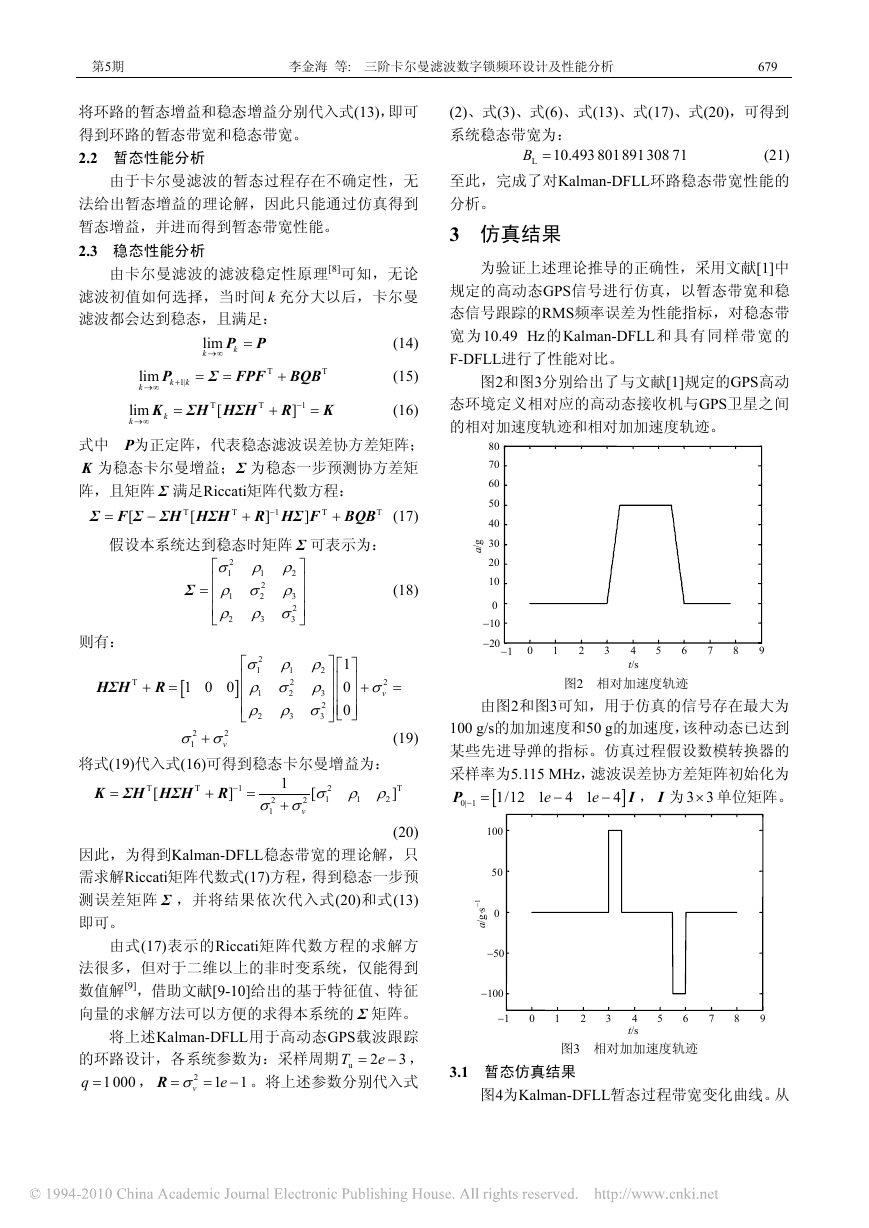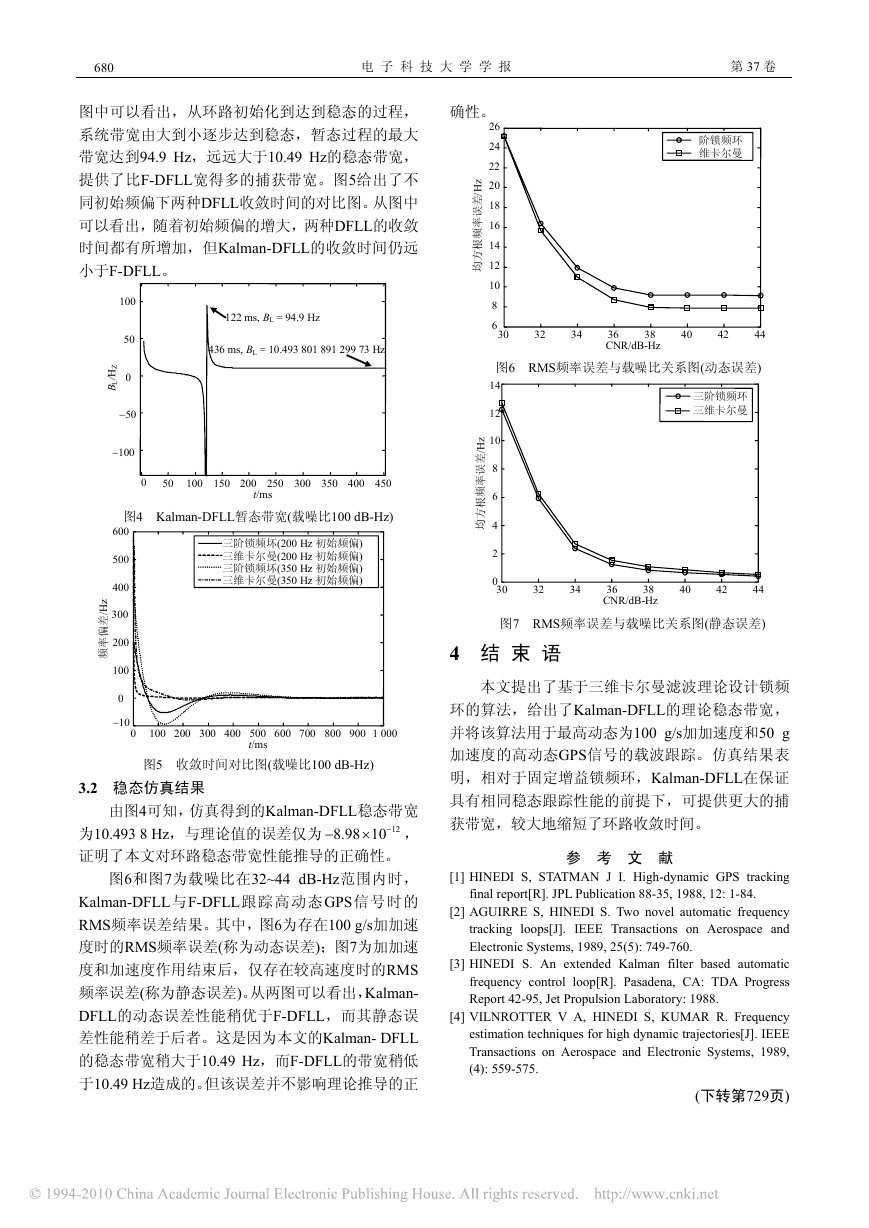 图2和图3分别给出了与文献[1]规定的GPS高动 态环境定义相对应的高动态接收机与GPS卫星之间 的相对加速度轨迹和相对加加速度轨迹。 80 70 60 50 40 30 20 10 g / a 0 −10 −20 −1 0 1 2 3 5 6 7 8 4 t/s 9 图2 相对加速度轨迹 由图2和图3可知，用于仿真的信号存在最大为 100 g/s的加加速度和50 g的加速度，该种动态已达到 某些先进导弹的指标。仿真过程假设数模转换器的 采样率为5.115 MHz，滤波误差协方差矩阵初始化为 I ， I 为 3 3× 单位矩阵。 P − = 0| 1 [ e 1/12 1 e 4 1 − − 4 ] 100 50 1 − s ⋅ g / a 0 −50 −100 −1 0 1 2 3 5 6 7 8 4 t/s 9 图3 相对加加速度轨迹 3.1 暂态仿真结果 图4为Kalman-DFLL暂态过程带宽变化曲线。从 

电 子 科 技 大 学 学 报 第 37 卷 680 图中可以看出，从环路初始化到达到稳态的过程， 系统带宽由大到小逐步达到稳态，暂态过程的最大 带宽达到94.9 Hz，远远大于10.49 Hz的稳态带宽， 提供了比F-DFLL宽得多的捕获带宽。图5给出了不 同初始频偏下两种DFLL收敛时间的对比图。从图中 可以看出，随着初始频偏的增大，两种DFLL的收敛 时间都有所增加，但Kalman-DFLL的收敛时间仍远 小于F-DFLL。 122 ms, BL = 94.9 Hz 436 ms, BL = 10.493 801 891 299 73 Hz 100 50 Z H / L B 0 −50 −100 0 50 100 150 200 250 300 350 400 450 图4 Kalman-DFLL暂态带宽(载噪比100 dB-Hz) 600 t/ms 三阶锁频坏(200 Hz 初始频偏) 三维卡尔曼(200 Hz 初始频偏) 三阶锁频坏(350 Hz 初始频偏) 三维卡尔曼(350 Hz 初始频偏) 500 400 300 200 100 / z H 差 偏 率 频 0 −10 0 100 200 300 400 500 600 700 800 900 1 000 t/ms 图5 收敛时间对比图(载噪比100 dB-Hz) 3.2 稳态仿真结果 由图4可知，仿真得到的Kalman-DFLL稳态带宽 ， 为10.493 8 Hz，与理论值的误差仅为 证明了本文对环路稳态带宽性能推导的正确性。 8.98 10− − × 12 图6和图7为载噪比在32~44 dB-Hz范围内时， Kalman-DFLL与F-DFLL跟踪高动态GPS信号时的 RMS频率误差结果。其中，图6为存在100 g/s加加速 度时的RMS频率误差(称为动态误差)；图7为加加速 度和加速度作用结束后，仅存在较高速度时的RMS 频率误差(称为静态误差)。从两图可以看出，Kalman- DFLL的动态误差性能稍优于F-DFLL，而其静态误 差性能稍差于后者。这是因为本文的Kalman- DFLL 的稳态带宽稍大于10.49 Hz，而F-DFLL的带宽稍低 于10.49 Hz造成的。但该误差并不影响理论推导的正 / 确性。 26 24 22 20 18 16 14 12 10 8 6 z H 差 误 率 频 根 方 均 30 阶锁频环 维卡尔曼 32 34 36 38 CNR/dB-Hz 40 42 44 图6 RMS频率误差与载噪比关系图(动态误差) 三阶锁频环 三维卡尔曼 / z H 差 误 率 频 根 方 均 14 12 10 8 6 4 2 0 30 32 34 36 38 CNR/dB-Hz 40 42 44 图7 RMS频率误差与载噪比关系图(静态误差) 4 结 束 语 本文提出了基于三维卡尔曼滤波理论设计锁频 环的算法，给出了Kalman-DFLL的理论稳态带宽， 并将该算法用于最高动态为100 g/s加加速度和50 g 加速度的高动态GPS信号的载波跟踪。仿真结果表 明，相对于固定增益锁频环，Kalman-DFLL在保证 具有相同稳态跟踪性能的前提下，可提供更大的捕 获带宽，较大地缩短了环路收敛时间。 参 考 文 献 [1] HINEDI S, STATMAN J I. High-dynamic GPS tracking final report[R]. JPL Publication 88-35, 1988, 12: 1-84. [2] AGUIRRE S, HINEDI S. Two novel automatic frequency tracking loops[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(5): 749-760. [3] HINEDI S. An extended Kalman filter based automatic frequency control loop[R]. Pasadena, CA: TDA Progress Report 42-95, Jet Propulsion Laboratory: 1988. [4] VILNROTTER V A, HINEDI S, KUMAR R. Frequency estimation techniques for high dynamic trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, (4): 559-575. (下转第729页) 

第5期 邬劭秩 等: K2PdX4:Cu2+超超精细参量研究 729 超超精细结构参量如表1所示。 2 讨 论 从表1中可以看出，本文所得到的理论值与实验 及文献[4]的结果比较符合，只采用2个调节参量，计 算也比文献[4]有一定程度的简化。由于在离子簇模 型基础上考虑了配体旋轨耦合作用以及配体p和s轨 道的贡献，并建立了分子轨道系数、未配对自旋密 度和平均共价因子等的关系，从而减少了所采用的 调节参量数目，因而具有较好的适用性。其次，从 配体Cl到Br共价性有所增加，而且旋轨耦合系数也 增大很多，中心离子与配体之间的电子云重叠(配体 轨道与Cu2+的3d轨道之间的混合)更加明显，使来自 配体轨道和旋轨耦合作用的贡献变得很重要而不能 忽略，与前人的研究结果[4]一致。再次，本文在处 理中仍存在一些误差(例如TX和TY比实验略大，而TZ 则偏小)，这可能是由于未考虑配体到金属的电荷转 移机制贡献以及离子簇模型本身的近似造成的，该 问题尚有待在今后的工作中作进一步的改进。 参 考 文 献 [1] SREEKANTH R P, CHAKTADHAR A, MURALI J, et al. Electron paramagnetic resonance and optical absorption studies of Cu2+ ions in alkali barium borate glasses[J]. J Alloys & Compounds, 1998, 265: 29-37. [2] APRAMAZ R, KARABULUT B, KOKSAL F. EPR spectra of VO2+ and Cu2+ ions in diammonium D-titrate single crystals[J]. J Phys Chem, 2000, 61: 1367-1372. [3] CHOW C, CHANG K, WILLETT R D. Electron spin resonance spectra and covalent bonding in the square-planar 2− ions[J]. J Chem Phys, 1973, 59: CuCl4 2629-2640. 2− and CuBr4 [4] ARAMBURU J A, MORENO M. Bonding in d9 complexes 2, and derived form EPR: Application to CuCl4 CdCl4 2: Cu2+[J]. J Chem Phys, 1985, 83(12): 6071-6083. 2−, CuBr4 [5] WU S Y, GAO X Y, WEI W H, et al. Investigations on the hyperfine and superhyperfine interaction parameters for Cs2GeF6: Mn4+[J]. Z Naturforsch, A, 2006, 60(2): 611-614. [6] FLETCHER R J, HANSEN J, LIVERMORE J, et al. Crystal structures, magnetic studies, and paramagnet resonance of the (4-picolinium)2Cu3Cl8, (4-picolinium)2 Cu3Cl8, and (1,1,4-t rimethylpiperazinium) Cu3Cl8[J]. Inorg Chem, 1983, 22: 330-334. trimmer copper stacks [7] CLEMENTS E, RAIMONDI D L. Atomic screaming constants from SCF functions[J]. J Chem Phys, 1963, 38: 2686-2689. [8] PATKER I H. Cu2+ in ammonium fluoride-a tetrahedral site[J]. J Phys Chem, 1971, 4(11): 2967-2978. [9] 游效曾. 配位化合物的结构与性质[M]. 天津: 科技出版 社, 1992. YOU Xiao-zeng. Structures and properties of coordination compounds[M]. Tianjin: Science and Technology Press, 1992. [10] MCPERSON G L, KACH R C, STUCKY G D. Electrons spin resonance spectra of V2+ , Mn2+, and Ni2+ in single crystals of CsMgBr3 and CsMgCl3[J]. J Chem Phys, 1974, 60: 1424-1431. 编 辑 黄 莘 ------------------------------------------------------------------------------------------------------------------------------------------- (上接第680页) DENG Zi-li, GUO Yi-xin. Analysis and application of filter, deconvolution, modern forecast and control[M]. Beijing: Affairs Press, 1988. series——Model, time [9] GREWAL M S, ANDREWS A P. Kalman filtering: theory and practice using matlab. Second Edition[M]. New York: John Wiley & Sons, Inc Publication, 2001. [10] ARNOLD W F, LAUB A J. Generalized eigenproblem algorithms and software for algebraic Riccati equations[J]. IEEE Proceedings, 1984, 72(12): 1746-1754. 编 辑 漆 蓉 [5] BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with applications tracking and navigation: Theory algorithms and software[M]. New York: John Wiley & Sons, Inc Publication, 2001. to [6] 张厥盛, 郑继禹, 万心平. 锁相技术[M]. 西安: 西安电子 科技大学出版社, 2005. ZHANG Jue-sheng, ZHENG Ji-yu, WAN Xin-ping. Phase-locked technique[M]. Xi’an: Xidian University Press, 2005. [7] JURY E I. Theory and application of the z-transform method[M]. New York: Wiley, 1964. [8] 邓自立, 郭一新. 现代时间序列分析及其应用——建模、 滤波、去卷、预报和控制[M]. 北京: 知识出版社, 1988.