SURF原论文翻译.pdf-资料库

hujingshuang-8611677-4744300845218958428.pdf-第1页.png

第1页 / 共11页

hujingshuang-8611677-4744300845218958428.pdf-第2页.png

第2页 / 共11页

hujingshuang-8611677-4744300845218958428.pdf-第3页.png

第3页 / 共11页

hujingshuang-8611677-4744300845218958428.pdf-第4页.png

第4页 / 共11页

hujingshuang-8611677-4744300845218958428.pdf-第5页.png

第5页 / 共11页

hujingshuang-8611677-4744300845218958428.pdf-第6页.png

第6页 / 共11页

hujingshuang-8611677-4744300845218958428.pdf-第7页.png

第7页 / 共11页

hujingshuang-8611677-4744300845218958428.pdf-第8页.png

第8页 / 共11页

SURF 学习笔记 Speed-Up Robust Features(SURF) SURF 是一种尺度，旋转不变的 detector 和 descriptor.最大的特点是快！在快的基础上保证性能（repeatability,distinctiveness 和 robustness）。 SURF 采用有效策略的主要有：1）积分图（用于对图像卷积）2）detector 是基于 Hessian 矩阵，descriptor 是基于分布的下面是 SURF 算法的具体实现： 1.兴趣点检测 SURF 对于兴趣点的检测是基于最基本的 Hessian 近似矩阵。 1.1 积分图像（由于不会在这里编辑公式，直接截图了）

PS：这里加一点自己的一点个人理解：关于矩形区域内像素点的求和应该是一种简单重复性运算，采用这种思路总体上提高了效率。为什么这么说呢？假设一幅图片共有 n 个像素点，则计算 n 个位置的积分图总共的加法运算有 n-1 次（注意：可不是次哦，要充分利用递推思想），将这些结果保存在一个跟原图对应的矩阵 M 中。当需要计算图像中某个矩形区域内的所有像素之和是直接像查表一样，调出 A,B,C,D 四点的积分图值，简单的加减法（注意只需要三次哦）即可得到结果。反之，如果采用 naive 的方式直接在原图像中的某个矩形区域内求和，你想想，总共可能的矩形组合有多少？！！且对于一幅图像 n 那是相当大啊，所以 2^n 那可是天文数字，而且这里面绝大部分的矩形有重叠，重叠意味着什么？在算求和的时候有重复性的工作，其实我们是可以有效的利用已经计算过的信息的。这就是积分图法的内在思想：它实际上是先计算 n 个互不重叠（专业点说是不相交）的矩形区域内的像素点求和，充分利用这些值（已有值）计算未知值，有点类似递推的味道...这就完全避免了重复求和运算。 1.2 用于检测兴趣点的 Hessian 矩阵作者 Herbert Bay 利用 Hessian 矩阵来检测兴趣点，具体是用 Hessian 矩阵行列式的最大值标记斑状结构（blob-like structure）的位置。同时，行列式值也作为尺度选择的依据，这里，作者是参考了 Lindeberg 的做法（'Feature detection with automatic scale selection'我还没有拜读原文！！）。说一下 Hessian 矩阵的定义：

中得到启发，采用了盒子型滤波器（box filter）对上面的滤波器进行近似。盒子型滤波器见图 1.3.

补充一点：filter 的响应还要根据 filter 的大小做一个归一化。这样做就可以保证对于任意大小的 filter 其 F 范数是统一的（这对于尺度不变性是有必要的）。有了前面的着一些准备工作，就可以对一幅图像 I 计算每个点的近似 Hessian 矩阵的行列式值，将这些值存储，备用！ 1.3 尺度空间表示算法的尺度不变性主要靠不同尺度下寻找感兴趣点。谈到不同尺度就不得不说‘金字塔’。Lowe 在其 SIFT 大作中是这样构造尺度空间的：对原图像不断地进行 Gauss 平滑+ 降采样。得到金字塔图像后，有进一步得到了 DoG 图，边和斑状结构就是通过 DoG 图得到其在原图的位置。

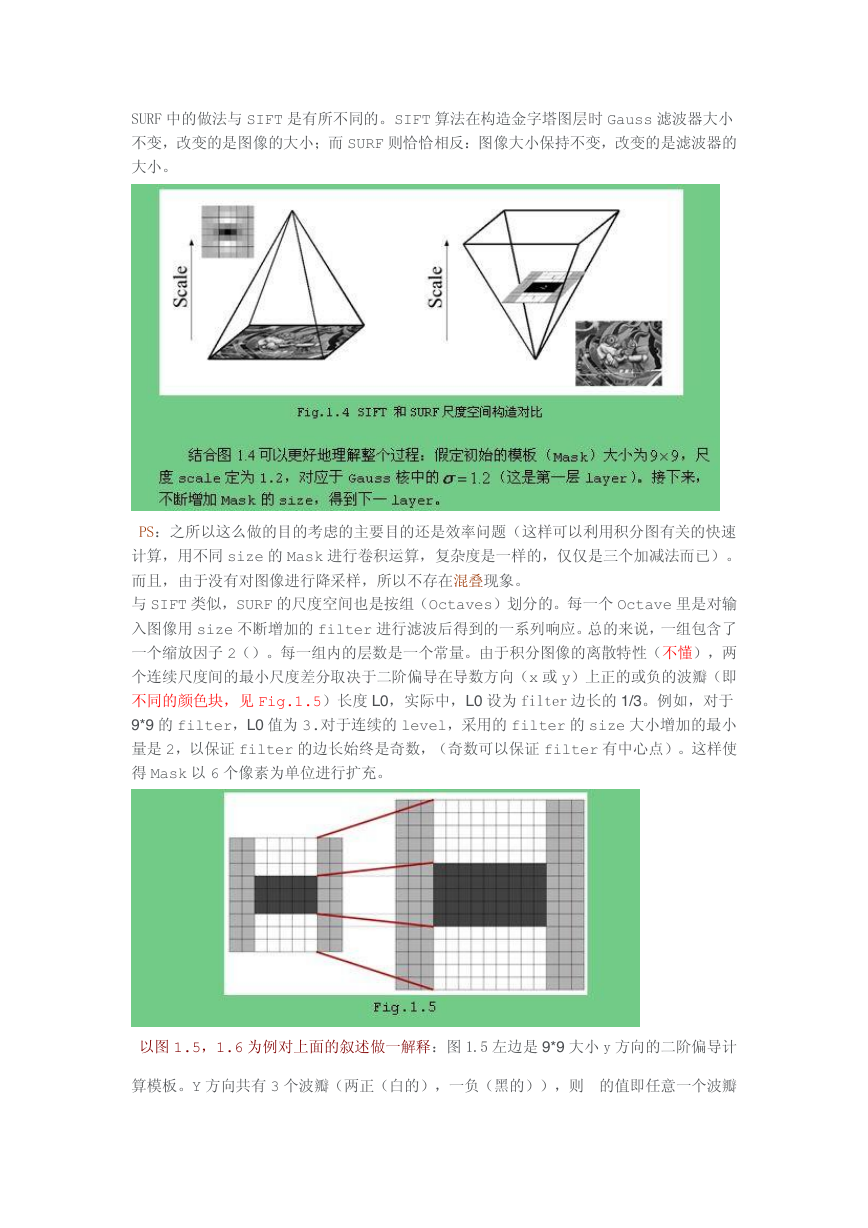
SURF 中的做法与 SIFT 是有所不同的。SIFT 算法在构造金字塔图层时 Gauss 滤波器大小不变，改变的是图像的大小；而 SURF 则恰恰相反：图像大小保持不变，改变的是滤波器的大小。 PS：之所以这么做的目的考虑的主要目的还是效率问题（这样可以利用积分图有关的快速计算，用不同 size 的 Mask 进行卷积运算，复杂度是一样的，仅仅是三个加减法而已）。而且，由于没有对图像进行降采样，所以不存在混叠现象。与 SIFT 类似，SURF 的尺度空间也是按组（Octaves）划分的。每一个 Octave 里是对输入图像用 size 不断增加的 filter 进行滤波后得到的一系列响应。总的来说，一组包含了一个缩放因子 2（）。每一组内的层数是一个常量。由于积分图像的离散特性（不懂），两个连续尺度间的最小尺度差分取决于二阶偏导在导数方向（x 或 y）上正的或负的波瓣（即不同的颜色块，见 Fig.1.5）长度 L0，实际中，L0 设为 filter 边长的 1/3。例如，对于 9*9 的 filter，L0 值为 3.对于连续的 level，采用的 filter 的 size 大小增加的最小量是 2，以保证 filter 的边长始终是奇数，（奇数可以保证 filter 有中心点）。这样使得 Mask 以 6 个像素为单位进行扩充。以图 1.5，1.6 为例对上面的叙述做一解释：图 1.5 左边是 9*9 大小 y 方向的二阶偏导计算模板。Y 方向共有 3 个波瓣（两正（白的），一负（黑的）），则的值即任意一个波瓣

的宽度。右边是对每个波瓣各扩充 2 个像素后的 filter，注意先是对波瓣扩充，即先扩宽，扩完后置于长怎么办，还没有搞懂.....貌似整体上最外的边（灰色的）是扩两个像素。 Fig.1.6 对于 Fig.1.6 左边是 x-y 方向的大小为 9*9 的 filter，每个对角方向各有两个波瓣（2 个黑的，2 个白的），对波瓣扩两个像素，得到右边的 filter。尺度空间的构造具体对于第一组（Octave）而言开始所用的是大小为 9*9 的 filter（最小的 scale），接下来的 filter 大小依次为 15*15，21*21，27*27，采用这些模板可以达到多于两个像素的尺度变化。作者说这么做是有必要的，原因是要对空域和相邻的尺度附近进行一个三维的非极大值抑制。（什么是非极大值抑制呢？字面意思：不是极大值就抑制。非极大值抑制通常用于边缘检测中边的进一步精简。举个简单例子，如果要从一些边缘中进一步提出水平边缘，那么就这么做：逐个检测边缘图中在水平方向的梯度值，如果不是局部极大值（非极大值），则就把该梯度值置 0（抑制））。由于要采用三维的非极大值抑制，那么 Hessian 响应图的首尾两个实际上是不包含极值信息的（这里跟 SIFT 算法里每一 Octave 里尽管有层，实际上只能利用中间的 7 层是一个道理）。因此，经过内插后（后面会讲到），可能的最小的尺度应该是，

由于组之间较大尺度的变化（从 9 到 15 变化倍数是 1.7）会带来较为粗糙的尺度采样，所以作者主张对尺度进行更为精细的采样来构造尺度空间。具体做法是：先用内插将图像大小加倍，然后用一个 size 为 15 的 filter 对加倍的图像进行滤波得到第一个 Octave 中的第一个响应图，随后用到的 filter 的 size 依次是 21,27,33 和 39.第二组类似，只不过此时相邻的两个 filter 的 size 差为 12 个像素，是第一组的两倍。第三组...类似。这样，两个 filter 之间的尺度变化就会相对变小了（15 到 21 变化倍数降为 1.4：21/15）。由于对任何 size 的 filter，F 范数模值是一个常量（？？？？）已经做了尺度上的归一化，所以对滤波器的响应不需要在加权了。 1.4 兴趣点的定位作者采用的是在 3*3*3 的邻域内进行非极大值抑制。具体是采用了文章 'Efficient Non- maxmum Supprerssion '中的做法（需要再进一步参考）。检测到的 Hessian 矩阵的行列式极大值还要在尺度和图像空间内做个内插，采用的方法可参见文章 'Invatiant Features from Interest Point Groups'.之所以要做内插，是因为每一组（Octave）的第一层（layer）的尺度（scale）差分是很大的。 2 兴趣点描述和匹配原文采用的 descriptor 跟 SIFT 类似也是基于兴趣点的邻域分布。具体是计算了 x 和 y 方向上的 Harr 小波值分布（具体的 Harr 小波也要研究一下），而不是梯度值分布。这样做同样是因为可以借助积分图加速运算，同时只用了 64 维信息。同时，根据 Laplacian 的符号，作者想出了一个新的 indexing 方法，既提高了鲁棒性，同时也加快了匹配过程。 2.1 方向分配为了具有方向不变性，作者为每个感兴趣点指定了一个可再复制（reproducible）的方向。做法如下：

① 再以 6s 为半径的圆形邻域计算在 x,y 方向的 Harr 小波响应，这里 s 指的是所要检测的兴趣点所处的尺度。 ② 采样步长设为 s,小波的 size 设为 4s,(这样又可以利用积分图进行快速滤波了) 图 2.1 分别是用来计算 x,y 方向上响应的 Haar 小波滤波器。 2.2 基于 Haar 小波响应的 Descriptor 对于 Descriptor 的提取，第一步是构造一个中心点在兴趣点附近，带方向（方向即前面所估计的方向）的方框。方框的大小设为 20s。方框具体形式课参考图 2.3.

资料库

SURF原论文翻译.pdf

相关推荐

课程资源

热门标签

最新资料