基于模糊控制的轨迹跟踪研究及仿真.docx-资料库

f8bba476-9b1d-4748-841a-3894611d0f1b.docx.pdf-第1页.png

第1页 / 共15页

f8bba476-9b1d-4748-841a-3894611d0f1b.docx.pdf-第2页.png

第2页 / 共15页

f8bba476-9b1d-4748-841a-3894611d0f1b.docx.pdf-第3页.png

第3页 / 共15页

f8bba476-9b1d-4748-841a-3894611d0f1b.docx.pdf-第4页.png

第4页 / 共15页

f8bba476-9b1d-4748-841a-3894611d0f1b.docx.pdf-第5页.png

第5页 / 共15页

f8bba476-9b1d-4748-841a-3894611d0f1b.docx.pdf-第6页.png

第6页 / 共15页

f8bba476-9b1d-4748-841a-3894611d0f1b.docx.pdf-第7页.png

第7页 / 共15页

f8bba476-9b1d-4748-841a-3894611d0f1b.docx.pdf-第8页.png

第8页 / 共15页

基于模糊控制的轨迹跟踪研究及仿真摘要：近年来，自动导引运输车（AGV）在物流运输等行业中得到广泛的应用，其控制问题尤其是轨迹跟踪问题随之彰显出来。AGV 小车的轨迹跟踪是非线性系统，传统的 PID 等控制方式难以满足稳定性与准确性的控制要求，而采用模糊控制系统能够有效地改善这种情况，从而能够较好地满足实际应用的需要。因此，本文提出了一种基于自适应模糊控制的控制器。本文首先建立了 AGV 小车的运动学模型，接着利用李雅普诺夫函数求解了控制律。其次，以 AGV 小车实际位姿与期望位姿的距离偏差和角度偏差作为模糊控制器的输入，以控制律中的比例因子作为输出，设计了自适应模糊控制器。最后，运用 matlab/simulink 对设计的系统进行了仿真，仿真结果说明该模糊控制器能够快速准确地跟踪任何合理的参考轨迹。关键词：AGV 小车，轨迹跟踪，模糊控制 Abstract: In recent years, AGV has been widely used in logistics and transportation industries. The control problems, especially the trajectory tracking problems, are highlighted. The trajectory tracking of the AGV car is a nonlinear system. The traditional control methods such as PID are difficult to meet the control requirements of stability and accuracy. However, the fuzzy control system can effectively improve the situation and thus can better meet the practical application needs. Therefore, this paper presents a controller based on adaptive fuzzy control. In this paper, the kinematics model of AGV car is built first, then the Lyapunov function is used to solve the control law. Secondly, taking the distance deviation and the angle deviation between the actual pose and the expected pose of the AGV car as the input of the fuzzy controller and the scale factor of the control law as the output, an adaptive fuzzy controller is designed. Finally, the designed system is simulated by using matlab / simulink. The simulation results show that the fuzzy controller can track any reasonable reference trajectory quickly and accurately. Key words: AGV car, trajectory tracking, fuzzy control 1

一、AGV 运动学模型 AGV 小车，结构如图 1-1 所示，前两轮为万向轮，称其为舵轮，控制小车方向。后两轮为驱动轮，提供动力。在不影响整体分析的情况下，可以把此自主导航车简化为左右两驱动轮的模型分析计算，建立模型。图 1-1 四轮 AGV 小车结构图如图 1-2 所示，AGV 小车的位姿由其两驱动轮的轴中点 M 在全局坐标系的，v 和 是小车的坐标及导航角来表示，即 AGV 小车当前位姿为 [ , 线速度和角速度，是小车模型的输入。 P  ]T x y  , 小车的运动学方程为：图 1-2 AGV 位姿坐标示意图  P     x      y              cos 0 sin 0 0 1            v        2 （1-1）

假设期望的轨迹为 q r  [ x y  r r , , r ]T ，期望的状态为[ v  ，AGV 小车模型 r ] , r 满足非完整移动机器人非完整约束条件，即公式 1-2：  x r sin  y r  r cos  r  0 （1-2）根据坐标转换，可得系统的误差方程为：     cos sin 0 -sin cos 0 0 0 1 x  e  y  e    e           p e   x x    r    y y                r r 对其误差方程求导可得位姿误差微分方程[1]：  p e    x  e   y  e     e               cos  e sin  e v v y    e r x v    r e -   r      （1-3）（1-4） AGV 小车轨迹跟踪的目标就是寻找控制律[ , v  ,使得对任意误差，系统的 ]T lim 误差方程均能收敛到 0，即 t  || ep || 0  。二、AGV 小车轨迹跟踪控制律设计根据小车的位姿误差微分方程，利用反演控制器设计的思想，设计合理的李雅普诺夫函数，并根据李雅普诺夫函数的稳定性条件可求得 AGV 小车轨迹跟踪的控制律。选取李雅普诺夫函数[2]为: V  1 2 2 (x e  2 y e )  1 2 k (1 cos   e ) (2-1) 将 2-1 式的李雅普诺夫函数对时间求一次导可得：  V  x e ( v   v r cos  e )  假定选取控制律为：  e (     r k v y 2 r e ) sin k 2 v            cos v  r e w k v y  r r 2 e   k x 1 e sin k 3  e    3 （2-2）（2-3）

将式 2-3 代入式（2-2）可得：  V   2 ( k x 1 e  k k 3 2 2 sin  e ) （2-4）当 1k ， 2k ， 3k 均大于零时，由式 2-2 和式 2-4 可知 0V  ,  ，满足李雅普诺夫渐进稳定的条件，因此选用式 2-3 的控制律满足 AGV 小车轨迹跟踪的条件。确定 1k ， 2k ， 3k 参数传统的方法要通过系统辨识，算法复杂，鲁棒性差[1]。因此，本文基于 AGV 小车实际位姿与期望位姿之间的距离偏差和角度偏差设计模糊控制器，实时调整参数，使系统具有较好的鲁棒性和稳定性。  0V 设计系统模型如果 2-1 所示：图 2-1 AGV 轨迹跟踪控制系统框图三、模糊控制器设计根据上文分析，控制律[ , v  中共有 1k ， 2k ， 3k 三个参数，因此需要设计三个模糊控制器。三个模糊控制器均采用距离偏差 d 和角度偏差 a 作为输入，分别输出 1k ， 2k ， 3k 。 ]T 3.1 输入、输出变量模糊化假定距离偏差 d 的值域为[0,5],角度偏差 a 的值域为[0,pi]。将 d 和 a 分为 7 个模糊集：SB（超大）、HB（很大）、B（大）、M（中等）、S（小）、HS（很小）、 SS（超小），论域均为[-6,6]。因此 d 的量化因子为 2 6  5 0  ，a 的量化因 2.4  dk  子为 ak  2 6  0 pi   12 pi 。假定 k1 的值域为[1,10],k2 的值域为[1,8],k2 的值域[1,8]。将 k1、k2 和 k3 分为 7 个模糊集：SB（超大）、HB（很大）、B（大）、M（中等）、S（小）、HS（很 4

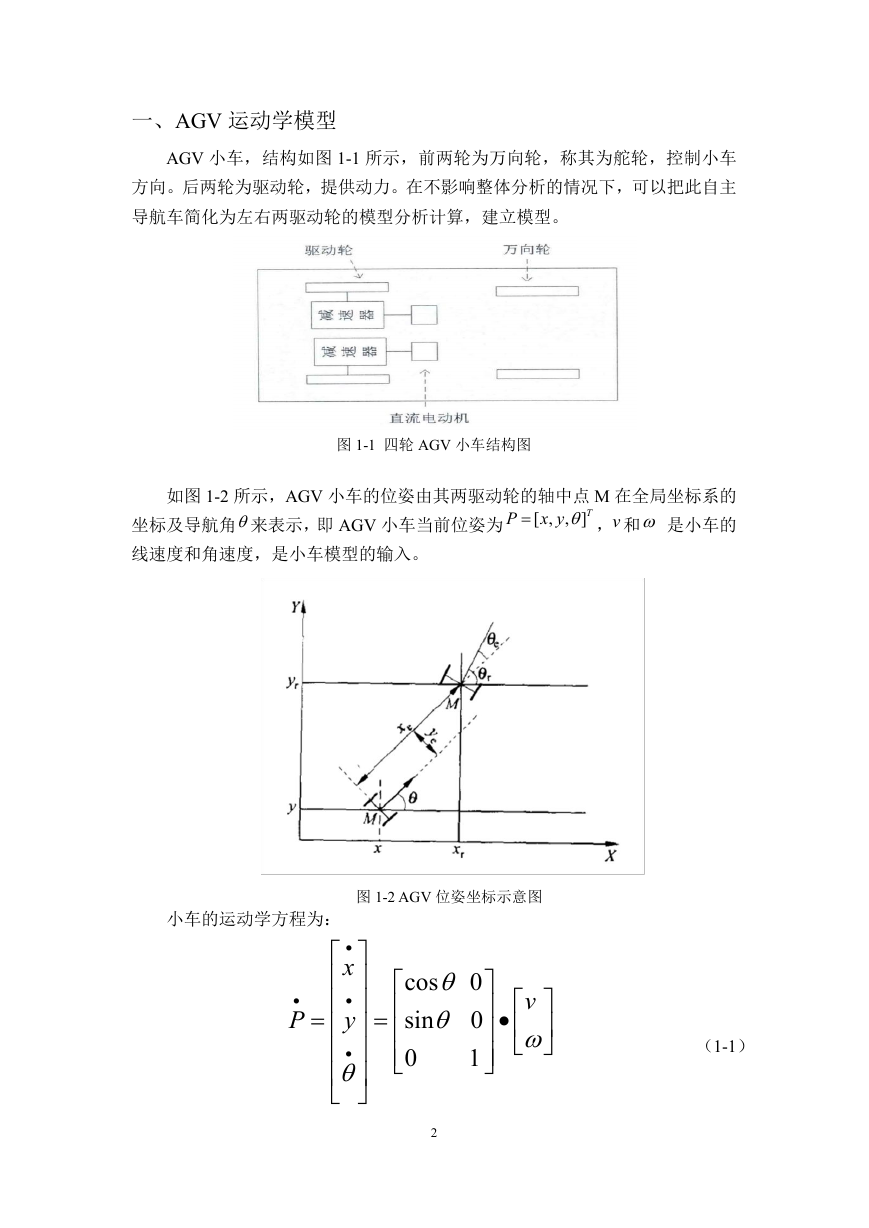
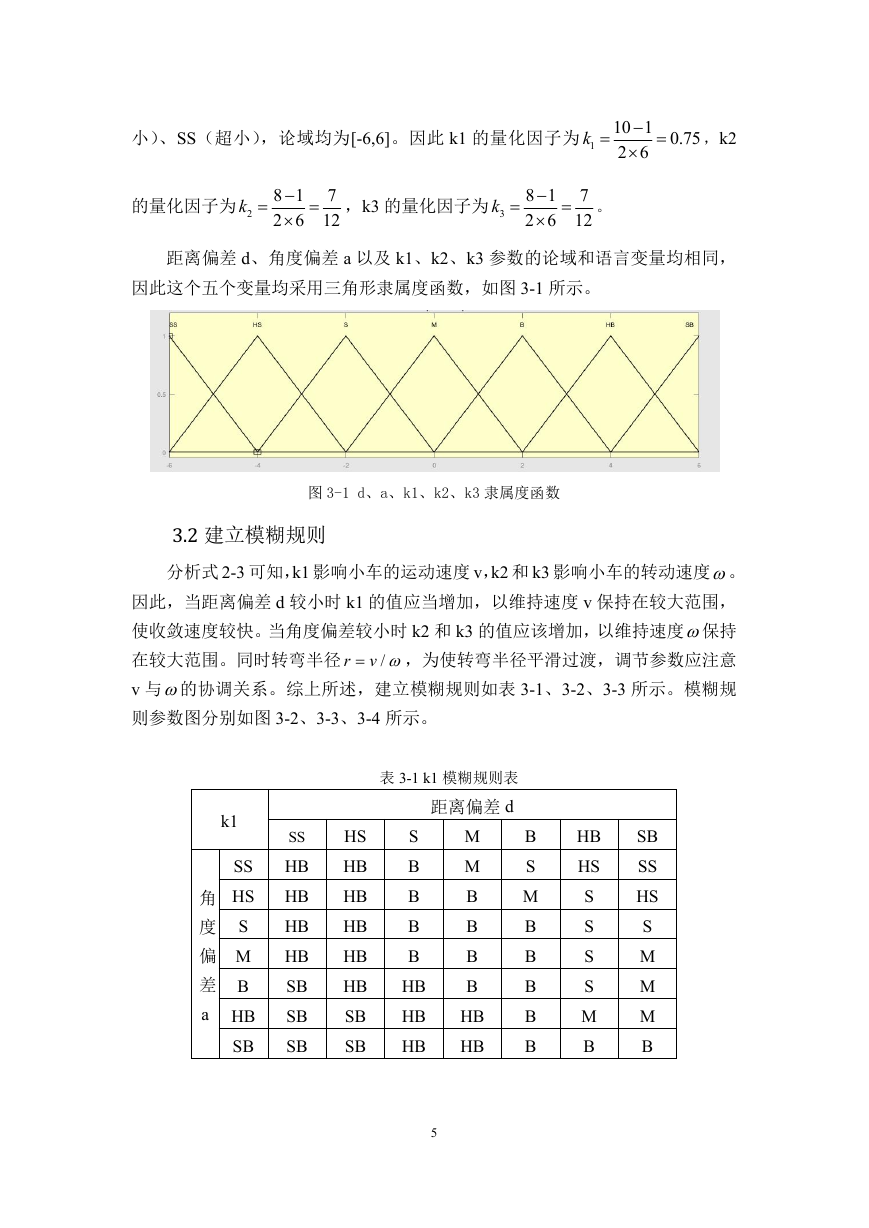
k 小）、SS（超小），论域均为[-6,6]。因此 k1 的量化因子为 1  10 1 0.75  2 6   ，k2 k 的量化因子为 2  8 1  2 6   7 12 k ，k3 的量化因子为 3  8 1  2 6   7 12 。距离偏差 d、角度偏差 a 以及 k1、k2、k3 参数的论域和语言变量均相同，因此这个五个变量均采用三角形隶属度函数，如图 3-1 所示。图 3-1 d、a、k1、k2、k3 隶属度函数 3.2 建立模糊规则分析式 2-3 可知，k1 影响小车的运动速度 v，k2 和 k3 影响小车的转动速度。因此，当距离偏差 d 较小时 k1 的值应当增加，以维持速度 v 保持在较大范围，使收敛速度较快。当角度偏差较小时 k2 和 k3 的值应该增加，以维持速度保持在较大范围。同时转弯半径，为使转弯半径平滑过渡，调节参数应注意 v 与的协调关系。综上所述，建立模糊规则如表 3-1、3-2、3-3 所示。模糊规则参数图分别如图 3-2、3-3、3-4 所示。 v  r / k1 SS HS S M B HB SB 角度偏差 a SS HB HB HB HB SB SB SB HS HB HB HB HB HB SB SB 表 3-1 k1 模糊规则表距离偏差 d M M B B B B HB HB B S M B B B B B HB HS S S S S M B SB SS HS S M M M B S B B B B HB HB HB 5

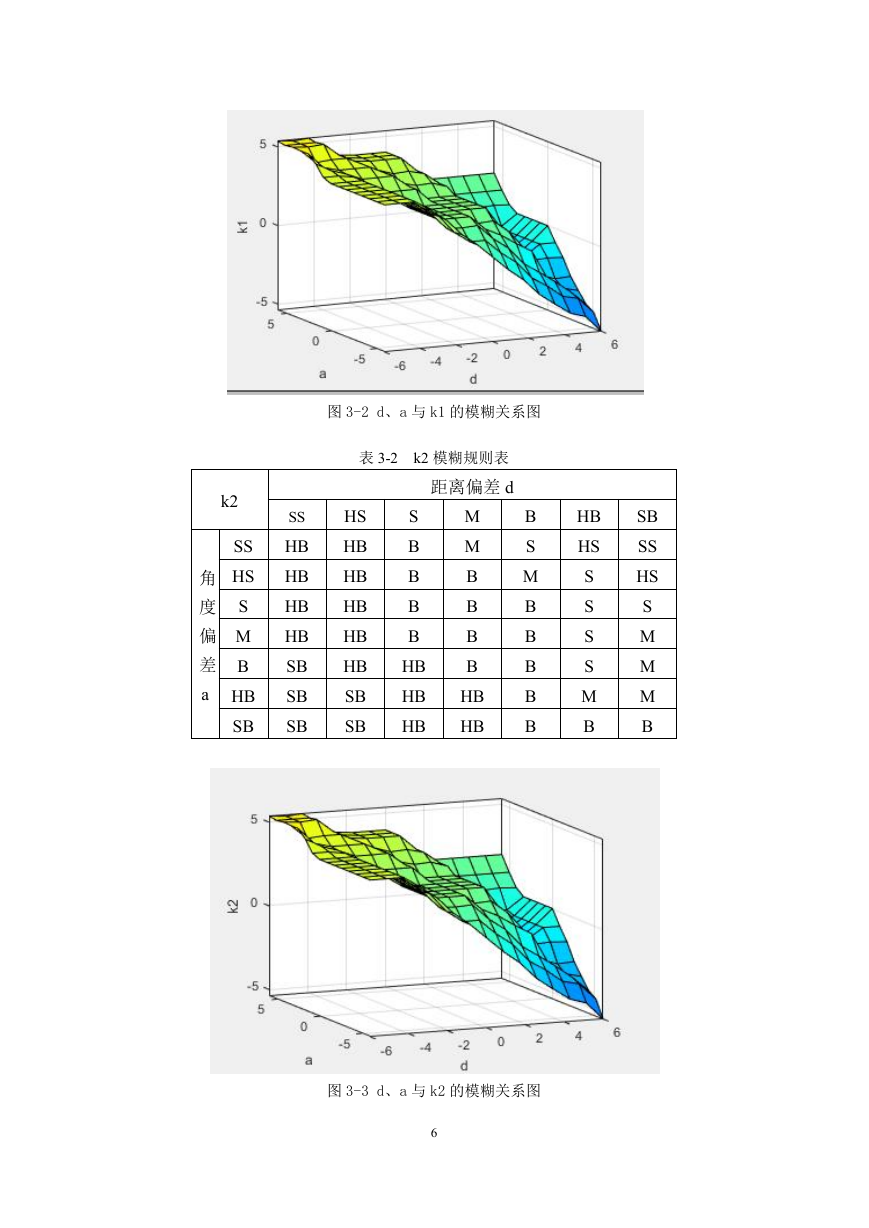
图 3-2 d、a 与 k1 的模糊关系图表 3-2 k2 模糊规则表距离偏差 d HS HB HB HB HB HB SB SB S B B B B HB HB HB M M B B B B HB HB B S M B B B B B k2 SS HS S M B HB SB 角度偏差 a SS HB HB HB HB SB SB SB HB HS S S S S M B SB SS HS S M M M B 图 3-3 d、a 与 k2 的模糊关系图 6

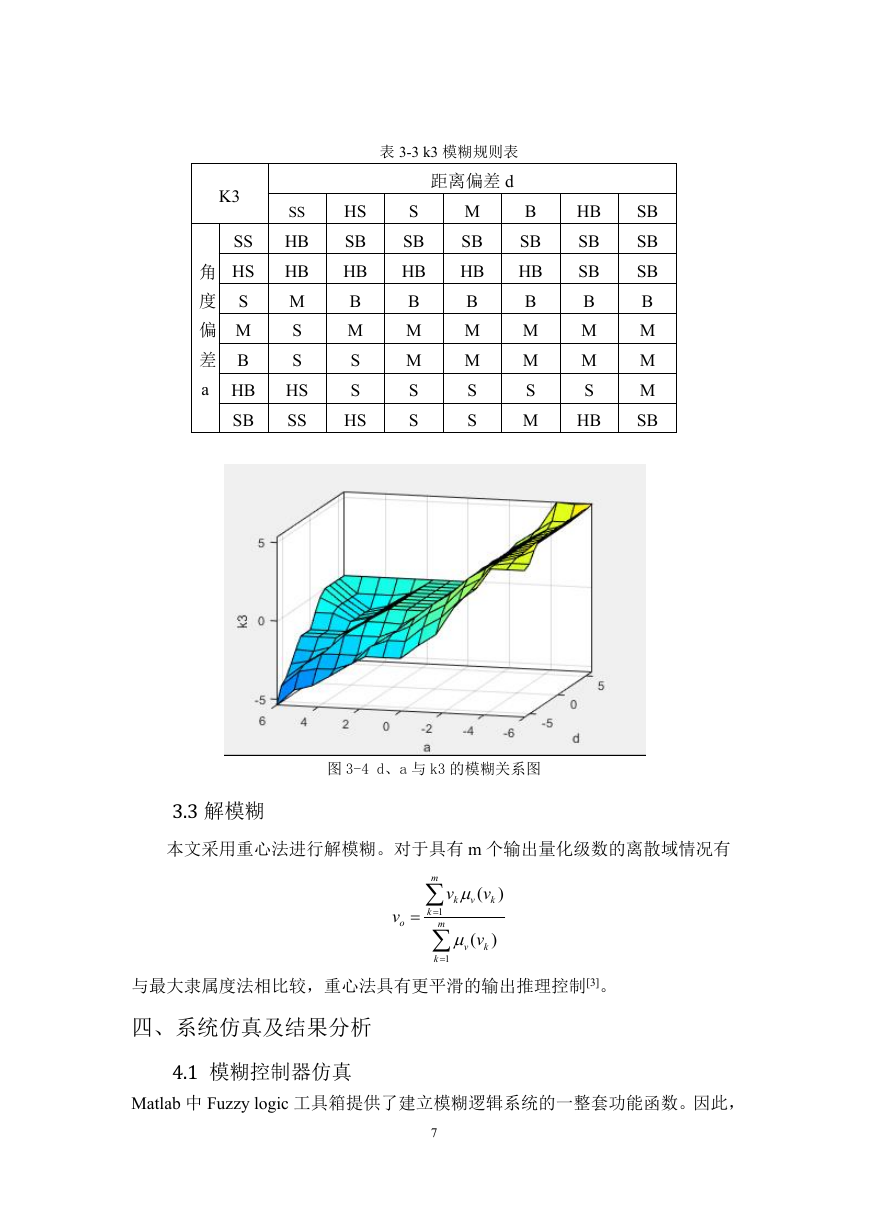
K3 SS HS S M B HB SB 角度偏差 a SS HB HB M S S HS SS 表 3-3 k3 模糊规则表距离偏差 d HS SB HB B M S S HS S SB HB B M M S S M SB HB B M M S S B SB HB B M M S M HB SB SB B M M S HB SB SB SB B M M M SB 图 3-4 d、a 与 k3 的模糊关系图 3.3 解模糊本文采用重心法进行解模糊。对于具有 m 个输出量化级数的离散域情况有 m v k  v ( v k )  v ( v k ) v o  k   1  m k 1  与最大隶属度法相比较，重心法具有更平滑的输出推理控制[3]。四、系统仿真及结果分析 4.1 模糊控制器仿真 7 Matlab 中 Fuzzy logic 工具箱提供了建立模糊逻辑系统的一整套功能函数。因此，

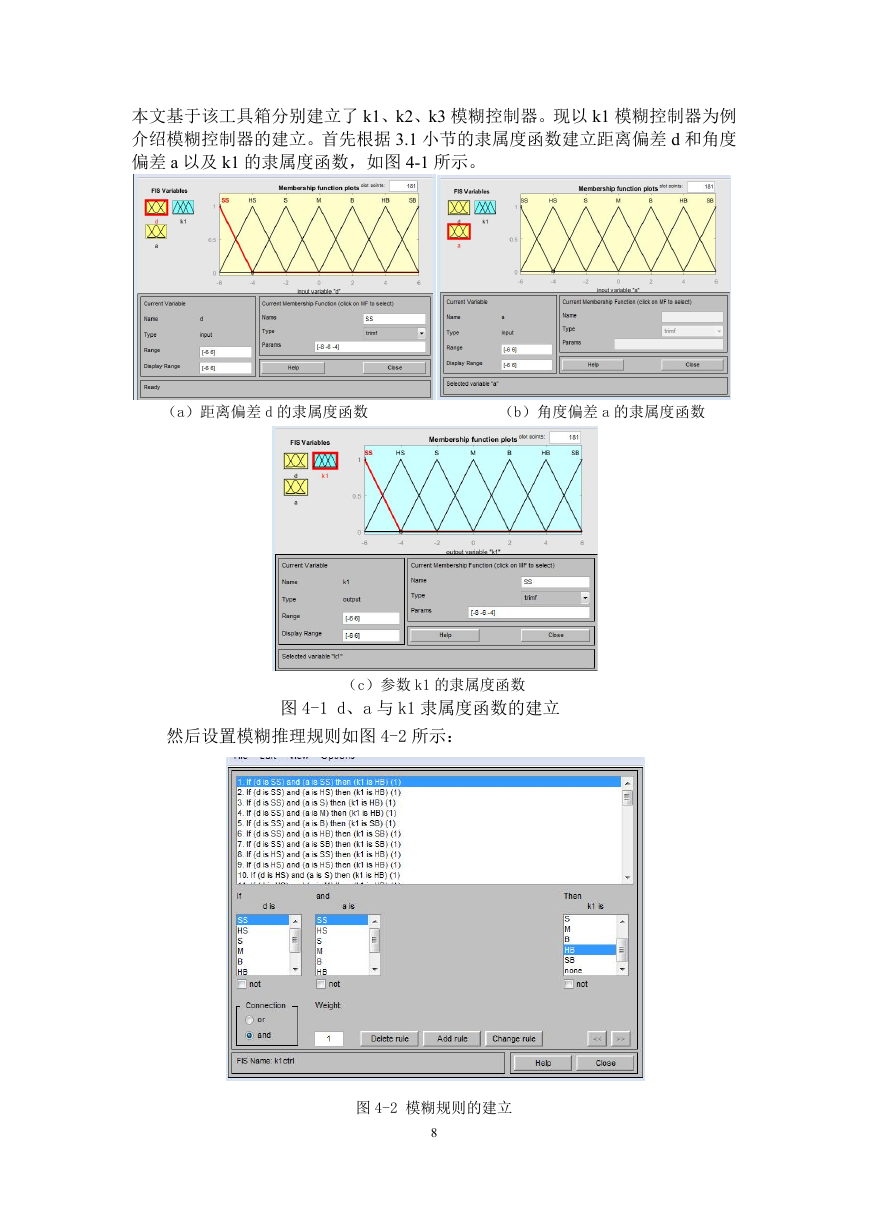
本文基于该工具箱分别建立了 k1、k2、k3 模糊控制器。现以 k1 模糊控制器为例介绍模糊控制器的建立。首先根据 3.1 小节的隶属度函数建立距离偏差 d 和角度偏差 a 以及 k1 的隶属度函数，如图 4-1 所示。（a）距离偏差 d 的隶属度函数（b）角度偏差 a 的隶属度函数（c）参数 k1 的隶属度函数图 4-1 d、a 与 k1 隶属度函数的建立然后设置模糊推理规则如图 4-2 所示：图 4-2 模糊规则的建立 8

资料库

基于模糊控制的轨迹跟踪研究及仿真.docx

相关推荐

人工智能

热门标签

最新资料