logo资料库

SPSS因子分析详细解读.docx

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.32M 资料格式：docx 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    SPSS因子分析详细解读 1． 因子分析简介 (1)概述 因子分析是研究相关矩阵或协方差矩阵的内部依赖关系，它将多个变量综合为少数几个 因子，以再现原始变量与因子之间的相关关系。 因子分析是主成分分析的推广和发展，也是利用降维方法进行统计分析的一种探索性分 析方法。 它的基本思想就是通过因子分析，将众多的原始变量转变为较少的几个因子；同时能有 效的解释原始变量的含义。 (2)其他概念 ①因子载荷 因子载荷是原始变量和因子之间的相关系数，它反映了因子对原始变量的重要作用和程 度。因子载荷的绝对值越接近1，则变量与因子的相关性越强。由此可以了解到因子的实际 含义，进而对因子进行命名。 当有多个因子的时候，因子载荷将构成-一个矩阵，称为因子载荷矩阵。 ②变量共同度 也就是变量方差，变量共同度就是所有因子对变量的解释贡献度和变量信息丢失程度； 其取值范围介于0和1之间，变量共同度越接近1，说明该变量能被因子解释的程度越高，变 量丢失的信息越少。 ③因子旋转 因子分析的结果需要每个因子都要有实际意义，有时，原始变量和因子之间的相关系数 可能无法明显地表达出因子的含义，为了使这些相关系数更加显著，可以对因子载荷矩阵进 行旋转，使原始变量和因子之间的关系更为突出，从而对因子的解释更加容易。 ④因子得分 因子得分可以用来评价每个个案在每个因子上的分值，该分值包含了原始变量的信息， 可以用于代替原始变量进行其他统计分析，比如回归分析、聚类分析等。 (3)目的 我们进行因子分析的原因主要有以下三个： 第一：原始变量之间存在一定的线性关系。因为变量之间的相关性较强时可以可用较少的因 子来概括其信息，便于探索结构；
    第二：将原始变量转化为因子得分后，可以利用因子得分形成的变量与其他变量进行其他统 计分析，比如回归分析、聚类分析等分析方法。 第三：将每个因子得分计算出综合得分，并进行综合评价。 (4)基本步骤 第一步：判断数据是否适合因子分析； 数据适合因子分析的标准有以下几点：  变量必须为连续变量，因为分类变量不适合直接进行因子分析；  变量之间存在一定的线性关系；  KMO统计量在0.5以下不适合因子分析，在0.7~0.8之间较适合因子分析，在0.8以上说明 数据极其适合因子分析。 第二步：构造因子变量。在分析之前选择合适的分析变量。 第三步：利用因子旋转方法，使得原始变量和因子之间的关系更为突出，从而能够明显地表 达因子的含义。 第四步：计算每个个案因子得分。 2. 因子分析实践 使用SPSS进行因子分析，使用的案例数据是足球球员的部分属性权重数据，如图K-1所 示。通过分析它们的权重，找出这些变量的共性，降低分析维度，并对各属性的球员进行比 较和综合评价。 图K-1 足球球员的部分属性权重数据 （1） 因子分析的操作步骤 在进行因子分析之前，首先需要通过其他的统计指标综合判断是否合适进行因子分析。 Step1：在SPSS中打开数据文件“足球球员的部分属性权重.sav”。单击【分析】菜单，选 择【降维】，从二级菜单中选择【因子】，弹出【因子分析】对话框，如图K-2所示
    图K-2【因子分析】对话框 Step2:将“速度”、“加速”、“耐力”、“平衡”、“盘带”、“传球”、“过人”、“镇 定”和“预判”这九个变量移至【变量】变量框中，作为待分析的变量。如图K-3所示。 图K-3 【因子分析】对话框 Step3：单击【描述】按钮，弹出【因子分析：描述】对话框，【相关性矩阵】框中指定考 察因子分析条件的方法及输出结果。勾选【系数(C)】和【KMO和巴特利特球形度检验】分别 用来判断原始变量之间是否存在一定的线性关系和是否适合采用因子分析方法提取因子。设 置完成后，确认无误，点击【继续】，返回主对话框。如图K-4所示。 图K-4【因子分析：描述】
    Step4：单击【提取】按钮，弹出【因子分析：提取】对话框，在【方法】框中提供了多种 提取因子的方法，最常用的方法是主成分分析法。在【输出】框勾选【碎石图】，主要是为 了辅助判断因子个数。其他均可默认，确认无误后，点击【继续】。如图K-5所示。 图K-5【因子分析：提取】 Step5：单击【旋转】按钮，弹出【因子分析：旋转】对话框，在【方法】框中选择因子旋 转方法。最常用的是最大方差法，用于更好地解释因子所包含的意义。【输出】可以选择解 或载荷图，一般可默认。设置完成后，点击【继续】。如图K-6所示。 图K-6【因子分析：旋转】 Step6：单击【得分】按钮，弹出【因子分析：得分】对话框，勾选【保存为变量】将因子 得分保存为变量；【方法】选择回归，用于保存计算得到的因子得分。设置完成，确认无误 后，点击【继续】。如图K-7所示。
    图K-7【因子分析：因子得分】 Step7：单击【选项】按钮，弹出【因子分析：选项】对话框，【缺失值】和【系数显示格 式】是指定缺失值的处理方法和因子载荷矩阵的输出方法；在【绝对值如下(A)】输入“.40”， 限制输出低于0.4的因子载荷，为了更清晰地显示因子载荷以及便于因子的解释和命名。如 图K-8所示。 Step8：全部设置完成后，点击【确定】进行因子分析。 图K-8【因子分析：选项】 （2）因子分析结果 ①第一个结果显示的是原始变量的相关性系数矩阵，可以看出有一些变量的相关系数比较高， 说明各变量之间存在相关关系，适合进行因子分析。 相关性矩阵 速度 加速 耐力 平衡 盘带 传球 过人 镇定 预判 相关 速度 1.000 .961 -.466 -.568 性 加速 .961 1.000 -.515 -.589 .204 .332 .198 .289 .153 -.735 -.566 .295 -.736 -.569 耐力 -.466 -.515 1.000 .899 -.240 -.130 -.076 .339 .265
    平衡 -.568 -.589 .899 1.000 -.392 -.328 -.209 .490 .404 盘带 .204 传球 .198 过人 .153 .332 .289 .295 -.240 -.392 1.000 .969 .964 -.202 -.216 -.130 -.328 .969 1.000 .926 -.252 -.283 -.076 -.209 .964 .926 1.000 -.121 -.151 镇定 -.735 -.736 预判 -.566 -.569 .339 .265 .490 -.202 -.252 -.121 1.000 .790 .404 -.216 -.283 -.151 .790 1.000 ②第二个结果是KMO 和巴特利特检验，用于检验数据是否适合因子分析；表中显示巴特利特 球形度检验F为1075.008，p值为0，小于0.01，存在显著差异；KMO统计量为0.650，介于0.5 和0.7之间，说明该数据可进行因子分析。 KMO 和巴特利特检验 KMO 取样适切性量数。 .650 巴特利特球形度检 近似卡方 1075.008 验 自由度 显著性 36 .000 ③第三个结果是公因子方差，也就是变量共同度；该结果显示了提取因子方法是主成分分析 法，原始变量初始解下的共同度均为1，以及能被提取因子所表示的程度；表中大部分变量 的共同度大于80%，说明有较少的信息丢失，各变量是可以被提取因子解释，因子分析效果 较好。 公因子方差 初始 提取 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 .833 .844 .956 .935 .996 .965 .964 .867 .734 速度 加速 耐力 平衡 盘带 传球 过人 镇定 预判 提取方法：主成分分析法。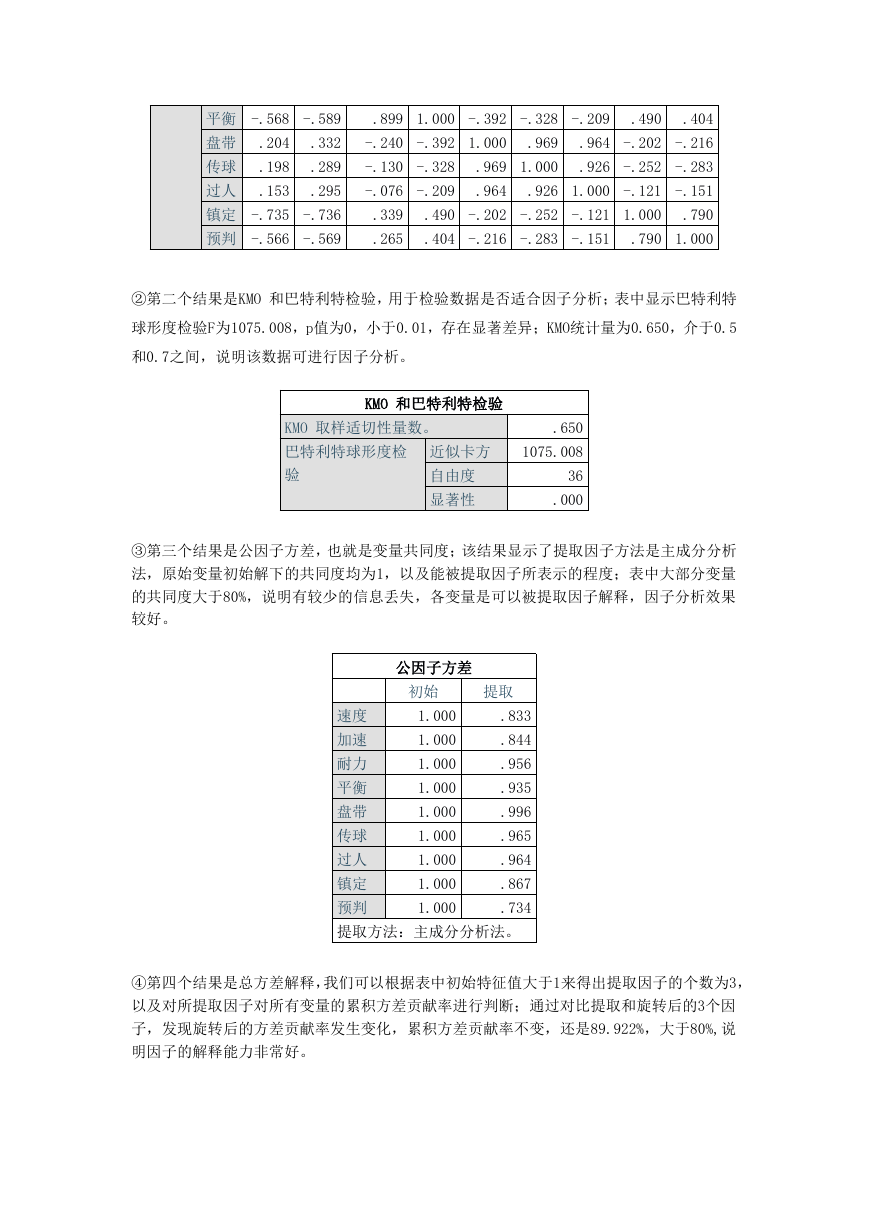 ④第四个结果是总方差解释，我们可以根据表中初始特征值大于1来得出提取因子的个数为3， 以及对所提取因子对所有变量的累积方差贡献率进行判断；通过对比提取和旋转后的3个因 子，发现旋转后的方差贡献率发生变化，累积方差贡献率不变，还是89.922%，大于80%,说 明因子的解释能力非常好。
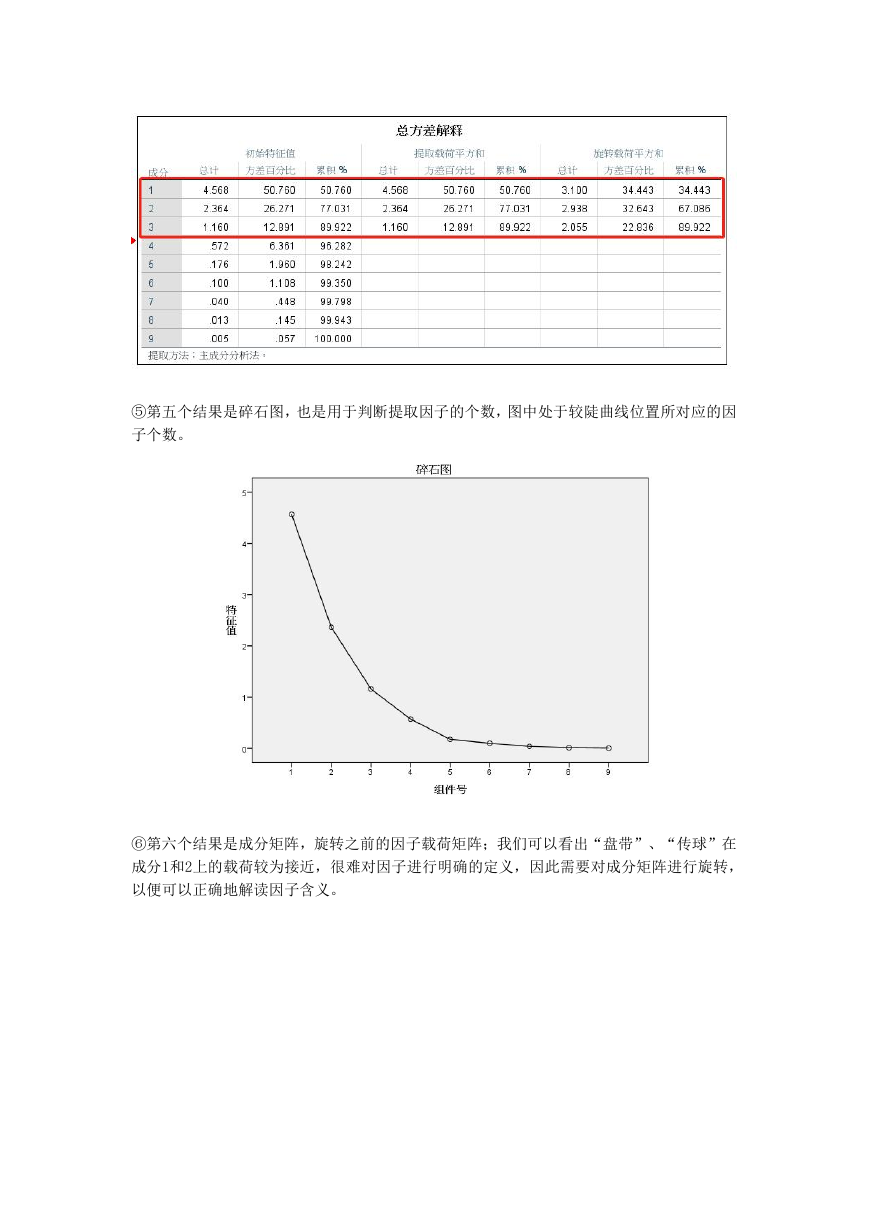
    ⑤第五个结果是碎石图，也是用于判断提取因子的个数，图中处于较陡曲线位置所对应的因 子个数。 ⑥第六个结果是成分矩阵，旋转之前的因子载荷矩阵；我们可以看出“盘带”、“传球”在 成分1和2上的载荷较为接近，很难对因子进行明确的定义，因此需要对成分矩阵进行旋转， 以便可以正确地解读因子含义。
    ⑦第七个结果是旋转后的成分矩阵，可以看出旋转后的因子载荷矩阵更清晰地因子含义；我 们发现表中第一因子载荷较大的变量是“镇定”、“预判”、“速度”和“加速”，说明这 四个变量与该因子的相关程度较强，其中“镇定”和“预判”表示的是精神属性，而“速度” 和“加速”反映的是身体属性，并且它们的载荷值符号为负，说明它们与该因子呈反向关系。 综上所述，我们可以把第一个因子命名为“精神属性”。 第二个因子载荷较大的变量是“过人”、“盘带”和“传球”，这三个变量与该因子是强正 相关性，并且它们反映的是技术属性。因此可命名为“技术属性”。 第三个因子载荷较大的变量是“耐力”和“平衡”，这两个变量与该因子的相关程度较强， 且反映的是身体属性。因此，可以将该因子命名为“身体属性”。 ⑧最后，将因子得分保存为变量，新增变量为“FAC1_1”、“FAC2_1”、“FAC3_1”，这3 个变量我们可看作原始变量经降维之后的结果，除了可以将它们与其他统计方法进行分析 (如聚类分析)之外；还可进行综合评价。 计算综合得分：进行加权计算，要考虑旋转后每个因子的方差贡献率占总累积方差贡献率的
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料