logo资料库

sigma-delta与小数分频.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.74M 资料格式：pdf 举报 版权申诉
第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
资料共8页，全文预览结束
    Sigma-delta 与小数分频 一、什么是 sigma-delta? Delta-Sigma(Δ-Σ)调制（或称 Sigma-Delta(Σ-Δ)调制、SDM，中文译作三角积分调制）。 Sigma-delta 调制器主要是由前端的积分器，一位 A/D 及反馈环路中的一位 D/A 来组成。其 主要组成框图如图 1.1。 图 1.1 选用一个 1 位 ADC(一个比较器)并以一个积分器的输出来驱动该比较器，然后将该 ADC 输出馈入一个 1 位 DAC 并将 1 位 DAC 的输出与输入信号的加和馈入积分器，便可得到一 阶 Σ-Δ 调制器。 由于这一系统包括一个 delta 调制器和一个积分器，积分器实际起到求和的作用，相 当于数学符号中 Σ 的功能，Sigma-delta 调制器因而得名。 二、小数分频杂散 2.1 小数分频的实现 锁相频率合成器的数字分频器本身无法实现小数分频。实际上，利用整数分频的数字 分频器可以采用一种平均的方法来完成小数分频。例如，虽然数字分频器本身不能实现 N=10.5 的小数分频，若能控制它先除一次 10，再除一次 11，这样交替进行，从输出的平 均频率看，就完成了 10.5 的小数分频。因此，只要能控制整数分频器的分频比按一定的 规则变化，就能实现小数分频。按照上述的概念，若要实现 N.F=4.25 的小数分频（N 表示 整数部分，F 表示小数部分），只要在每 4 次分频中，作 3 次除 4，再作 1 次除 5，就可得 到 N.F=(5×1+4×3)/4=4.25 （图 2.1.1）。 fo = N. Ffr = (N + a Q ) fr = N(Q − a) + (N + 1)a Q 式中，a 和 Q 都是正整数。完成 N.F 分频，是将 fo 在 Q 个参考周期 Tr 中进行（Q-a） 次 N 分频和 a 次 N+1 分频来进行的，0.F=a/Q。 图 2.1.2
    2.2 瞬时与平均 由上面的框图可以看出，小数分频的实现并不困难，但在其实现过程中也存着一些问 题。即由于小数分频的实现过程决定，分频器输出的瞬时频率与参考频率并不相等，使得 鉴相器产生锯齿形的相位误差，这一相位误差通过环路滤波加到压控振荡器上，会在压控 振荡器的输出频率上产生杂散，影响了小数分频的频谱纯度及性能。下面一节就对小数分 频中相位误差的产生及后面的杂散产作了详细地分析。 2.3 相位误差与杂散 从上面小数分频的工作过程可知，分频器输出脉冲瞬时频率不等于参考信号频率，因而使输入到 鉴相器的两路信号脉冲的前沿存在一个时间差，这个时间差就使鉴相器产生一个相应的相差，而且这 个相差逐周期累积，如图 2.3.1 所示。 图 2.3.1 当分频器输出频率为 fo/N+1 时，这个累积的相差减小，直至完成 QTr 时，相差才减小至零，然后 相位误差累积又开始新的周期，如图 2.3.2。这种相位误差累积使鉴相器输出相应的周期性锯齿形阶梯 电压波形，以 N=4.25 为例，归一化相位误差如图 2.3.3 所示。 图 2.3.2 图 2.3.3 由于这个锯齿形阶梯波的周期为 QTr，其谐波分量频率较低，它将通过环路滤波器对压控振荡器 进行周期性的频率调制，产生输出寄生杂散，这是由于小数分频带来的调制影响，这种杂散就称为小 数杂散。 2.4 杂散与量化噪声 Σ-Δ 调制器被用在小数分频器中时，分频的小数位相当于 Σ-Δ 调制器中 A/D 转换器的
    模拟输入，整数分频数则类似于 Σ-Δ 调制器中的 1 位量化器，即对输入的小数位.F 进行了 1 位量化，从而引入了量化误差 Q。该量化误差与鉴相器输出的相位误差成正比，是形成 小数分频相位杂散的根本原因。抑制小数相位杂散，即可以通过对量化误差进行再次处理 的方法来实现。 三、Sigma-delta 调制与量化噪声 Σ-Δ 调制器就是将输入信号以远超过奈奎斯特频率的采样频率进行高速采样，对每个 采样信号量化位数常采用 1 位，通常又称为 1 位采样 A/D 转换器。Σ-Δ 调制器正是通过这 一过采样技术及反馈环本身的结构对由于 A/D 变换产生的量化噪声进行整形，使其变化到 信号带宽之外。 3.1 Σ-Δ 调制与 PCM Σ-Δ 调制源自脉冲码调制(PCM)系统的早期研发阶段，尤其是那些与称为“Δ 调制”和“差 分 PCM”的传输技术相关的。 Δ 调制和差分 PCM 的重要驱动力是通过传输连续样本之间的 数值变化(Δ)而非真实样本自身，以实现更高的传输效率。 在 Δ 调制中，模拟信号通过 1 位 ADC(比较器)进行量化，如图 3.1.1A 所示。比较器输 出由 1 位 DAC 转回为模拟信号，并在通过积分器后从输入中减去。模拟信号波形的传送方 式如下："1"表示自上次采样后出现正偏移，而"0"则表示自上次采样之后出现负偏移。 图 3.1.1 Δ 调制与差分 PCM 图 3.1.2 Δ 调制进行量化 如果模拟信号在一定时间内保持固定的直流电平，则会获得"0"和"1"交替形式。应注 意，差分 PCM(见图 3.1.1B)采用几乎完全相同的概念，不同之处仅在于其采用多位 ADC 而 非单个比较器来获得所传送的信息。由于并没有限制同符号脉冲的出现次数，因此 Δ 调制 系统能够跟踪任何幅度的信号。理论上不存在峰值削波。不过，Δ 调制在理论上存在一定 局限性，即模拟信号不可快速变化。斜率削波问题如图 3.1.2 所示。图中，虽然每个采样 时刻都指示正偏移，但模拟信号上升过快，因此量化器无法保持同步。为此，Δ 调制和差 分 PCM 从未广泛流行开来，但只要对 Δ 型调制器稍微进行一些修改便可得到基本的 Σ-Δ 架构（图 1.1）。 3.2 过采样与噪声整形 要弄清楚 Σ-Δ 调制的工作原理，需要熟悉过采样、量化噪声整形和滤波等概念。接下 来，我们借助频域分析来看看过采样技术。当直流转换具有多达 1/2 LSB 的量化误差时，
    数据采样系统便存在量化噪声。理想的经典 N 位采样 ADC 在 DC 至 fs/2 的奈奎斯特频段范 围内均匀地分布着均方根大小为 q/√12的量化噪声(其中，q 是一个 LSB 的值而 fs 是采样频 率)，如图 3.2.1A 所示 。 如果选择更高的采样速率 Kfs(见图 3.2.1B)，均方根量化噪声保持为 q/√12，但该噪声 现在分布在 DC 至 Kfs/2 这个更宽的带宽范围内。如果接着在输出端应用数字低通滤波器 (LPF)，则可以消除多数量化噪声，而又不会影响所需信号，从而使得 SNR 得以改善 。系 数 K 通常称为“过采样率”。注意，从这一点看，过采样还有一个好处，那就是可降低对模 拟抗混叠滤波器的要求，这是 Σ-Δ 调制的一项巨大优势 。 图 3.2.1 过采样和噪声整形 如果只是采用过采样来提高分辨率， Σ-Δ 调制器还会对量化噪声进行整形，以使此 类噪声大多数位于此通带之外，如图 3.2.1C 所示。 3.3 Σ-Δ 调制器分析和噪声整形 下面就以 A/D 变换的量化噪声为起点，通过对过采样原理及 Σ-Δ 调制器结构的分析来 分析其噪声整形特性。 Σ-Δ 技术就是将输入信号以远超过奈奎斯特频率的采样频率进行高速采样，对每个采 样信号量化位数常采用 1 位，通常又称为 1 位采样 A/D 转换器。Σ-Δ 调制器正是通过这一 过采样技术及反馈环本身的结构对由于 A/D 变换产生的量化噪声进行整形，使其变化到信 号带宽之外。 Σ-Δ 调制器频域内简单模型如图 3.3.1， 调制器中的积分器表示为传递函数等于 H(f) = 1/f 的模拟低通滤波器。此传递函数具有与输入频率成反比的幅度响应。1 位量化器产生量 化噪声 Q，量化噪声 Q 被注入输出求和模块。
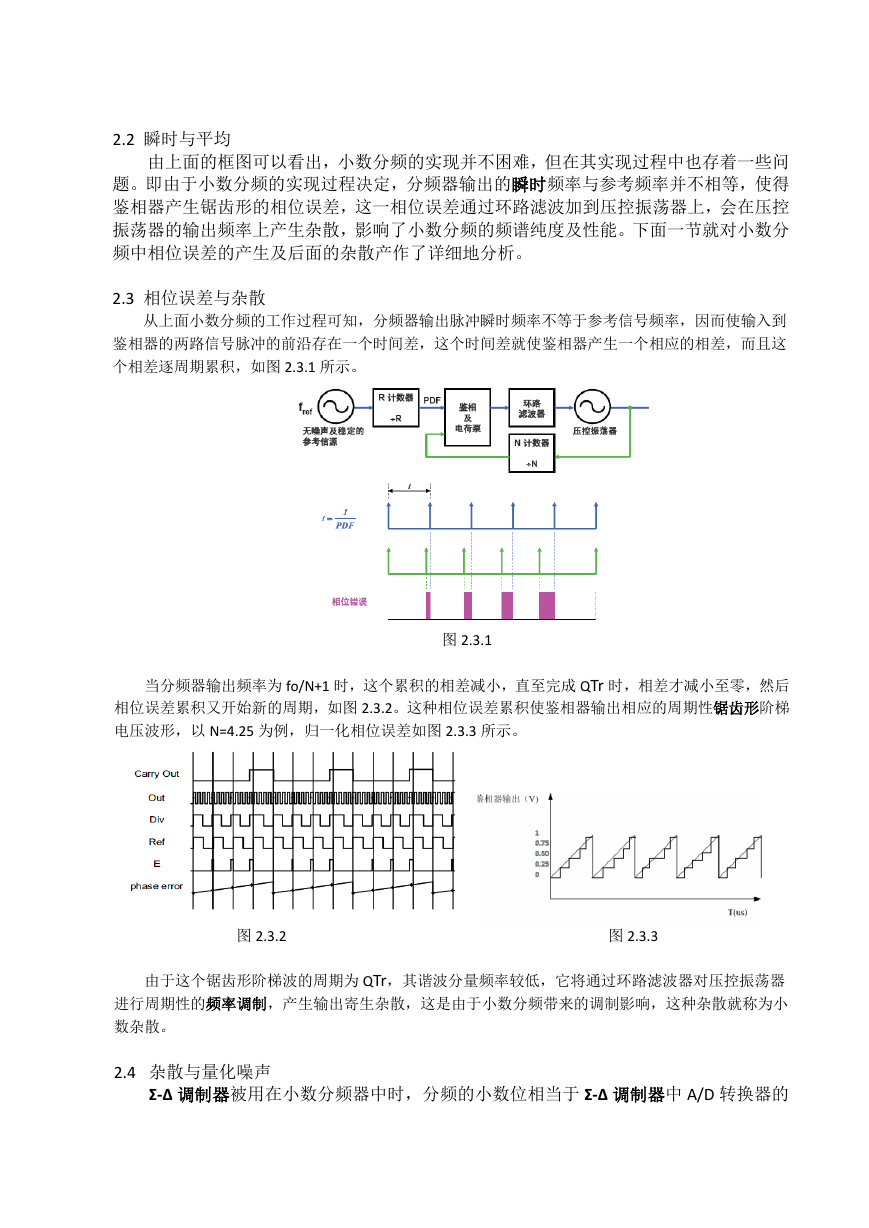
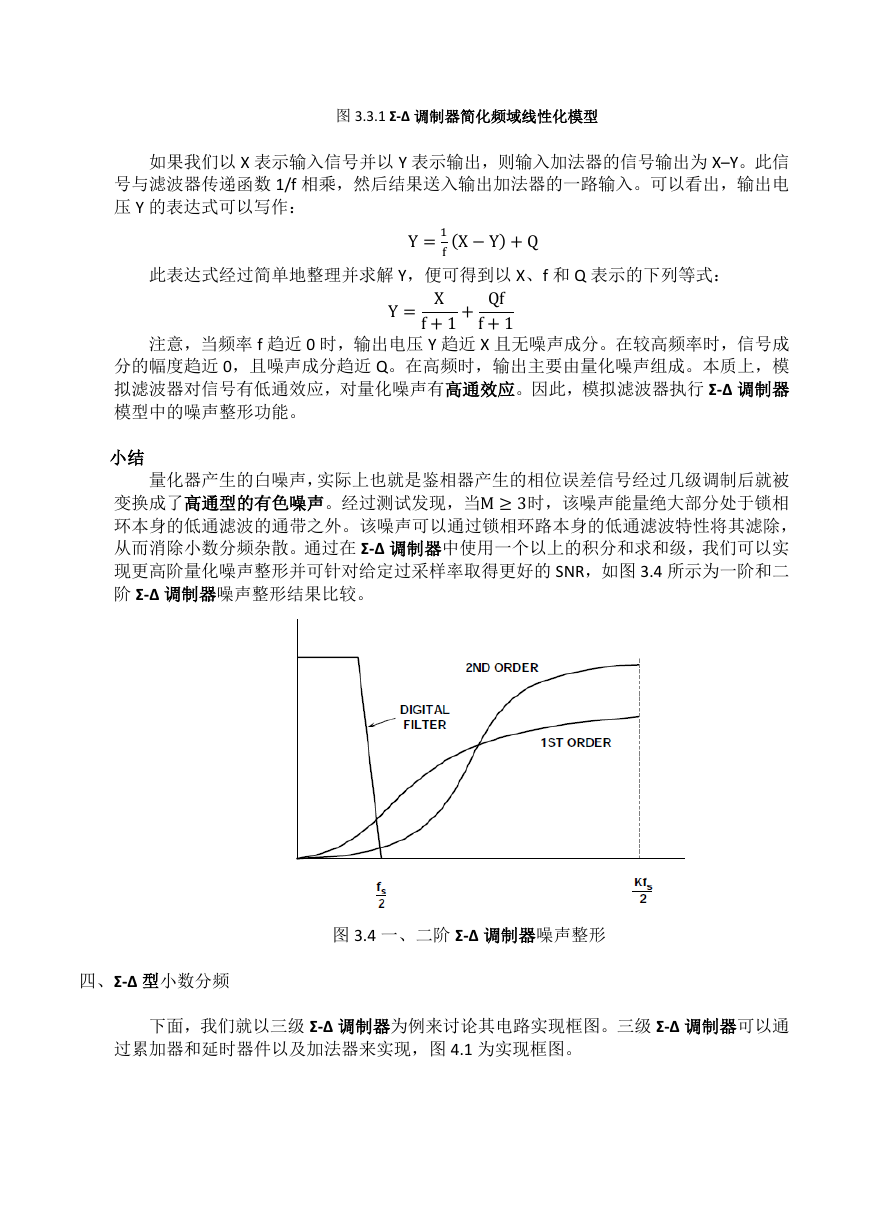
    图 3.3.1 Σ-Δ 调制器简化频域线性化模型 如果我们以 X 表示输入信号并以 Y 表示输出，则输入加法器的信号输出为 X–Y。此信 号与滤波器传递函数 1/f 相乘，然后结果送入输出加法器的一路输入。可以看出，输出电 压 Y 的表达式可以写作： 此表达式经过简单地整理并求解 Y，便可得到以 X、f 和 Q 表示的下列等式： Y = 1 f (X − Y) + Q Y = X f + 1 + Qf f + 1 注意，当频率 f 趋近 0 时，输出电压 Y 趋近 X 且无噪声成分。在较高频率时，信号成 分的幅度趋近 0，且噪声成分趋近 Q。在高频时，输出主要由量化噪声组成。本质上，模 拟滤波器对信号有低通效应，对量化噪声有高通效应。因此，模拟滤波器执行 Σ-Δ 调制器 模型中的噪声整形功能。 小结 量化器产生的白噪声，实际上也就是鉴相器产生的相位误差信号经过几级调制后就被 变换成了高通型的有色噪声。经过测试发现，当M ≥ 3时，该噪声能量绝大部分处于锁相 环本身的低通滤波的通带之外。该噪声可以通过锁相环路本身的低通滤波特性将其滤除， 从而消除小数分频杂散。通过在 Σ-Δ 调制器中使用一个以上的积分和求和级，我们可以实 现更高阶量化噪声整形并可针对给定过采样率取得更好的 SNR，如图 3.4 所示为一阶和二 阶 Σ-Δ 调制器噪声整形结果比较。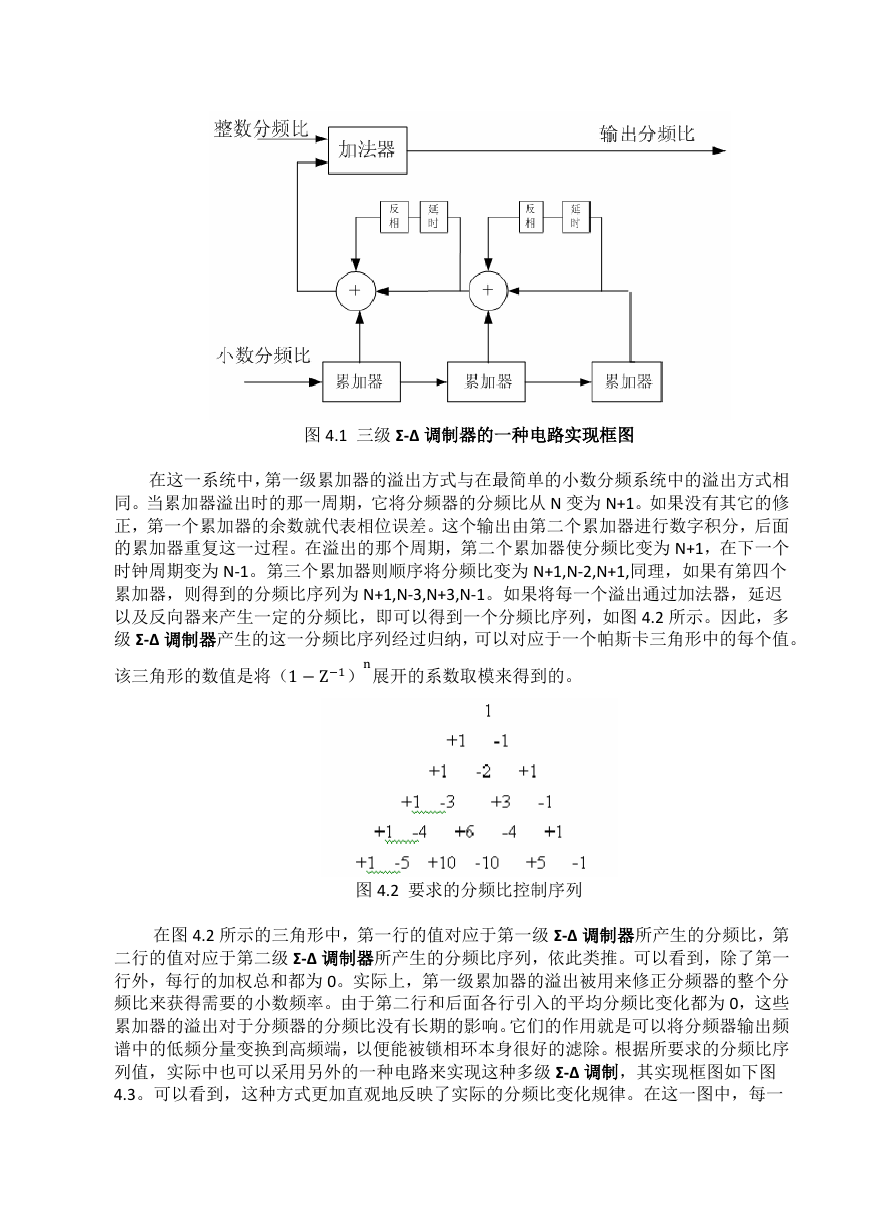 图 3.4 一、二阶 Σ-Δ 调制器噪声整形 四、Σ-Δ 型小数分频 下面，我们就以三级 Σ-Δ 调制器为例来讨论其电路实现框图。三级 Σ-Δ 调制器可以通 过累加器和延时器件以及加法器来实现，图 4.1 为实现框图。
    图 4.1 三级 Σ-Δ 调制器的一种电路实现框图 在这一系统中，第一级累加器的溢出方式与在最简单的小数分频系统中的溢出方式相 同。当累加器溢出时的那一周期，它将分频器的分频比从 N 变为 N+1。如果没有其它的修 正，第一个累加器的余数就代表相位误差。这个输出由第二个累加器进行数字积分，后面 的累加器重复这一过程。在溢出的那个周期，第二个累加器使分频比变为 N+1，在下一个 时钟周期变为 N-1。第三个累加器则顺序将分频比变为 N+1,N-2,N+1,同理，如果有第四个 累加器，则得到的分频比序列为 N+1,N-3,N+3,N-1。如果将每一个溢出通过加法器，延迟 以及反向器来产生一定的分频比，即可以得到一个分频比序列，如图 4.2 所示。因此，多 级 Σ-Δ 调制器产生的这一分频比序列经过归纳，可以对应于一个帕斯卡三角形中的每个值。 该三角形的数值是将（1 − Z−1） n 展开的系数取模来得到的。 图 4.2 要求的分频比控制序列 在图 4.2 所示的三角形中，第一行的值对应于第一级 Σ-Δ 调制器所产生的分频比，第 二行的值对应于第二级 Σ-Δ 调制器所产生的分频比序列，依此类推。可以看到，除了第一 行外，每行的加权总和都为 0。实际上，第一级累加器的溢出被用来修正分频器的整个分 频比来获得需要的小数频率。由于第二行和后面各行引入的平均分频比变化都为 0，这些 累加器的溢出对于分频器的分频比没有长期的影响。它们的作用就是可以将分频器输出频 谱中的低频分量变换到高频端，以便能被锁相环本身很好的滤除。根据所要求的分频比序 列值，实际中也可以采用另外的一种电路来实现这种多级 Σ-Δ 调制，其实现框图如下图 4.3。可以看到，这种方式更加直观地反映了实际的分频比变化规律。在这一图中，每一
    个累加器的输出被连在下一个累加器的输入上。同时，每一个累加器的溢出被用来控制数 值相加器的加数值，每个参考周期用这些加数值相加的结果再与整数分频数的和来控制整 数分频器的分频比。利用这一电路，就实现了上面所要求的控制分频比。 第 1 级调制器 N 计数器交替采用 N 与 N+1 这两个数值 第 2 级调制器 N 计数器交替采用 N-1、N、N+1 及 N+2 这 4 个数值 第 3 级调制器 N 计数器交替采用 N-3、N-2、N-1、N、N+1、N+2、N+3 及 N+4 这几个数值 第 k 级调制器 N 计数器交替采用N − 2k−1 + 1，……，N + 2k−1 理论上，第 N 级 delta sigma 锁相环的杂散应少于第 N-1 级 delta sigma 锁相环。 由于多级累加器是在一个周期内完成累加功能的，后面的累加器溢出更容易发生， 在时间上出现更早，因此，累加器的不断溢出，互相叠加，相位修正在该周期内就更早， 更经常发生。使用更多的累加器可以使相位误差得到更好的抵消，获得高质量输出频率。 总结 图 4.3 三级 Σ-Δ 调制器的另一种电路实现框图 分频器很多情况下只能实现整数分频，为了实现小数分频，动态地改变分频比，使得 平均效果是小数。但问题是：究竟怎么动态地改变分频比好呢？一种是用白噪声频谱形状 的伪随机数列来改变分频比，分频比每个时刻都与理想的小数分频比不相等，但平均起来 是相等的，这就产生量化噪声。这样做会发现带内噪声因为这些白噪声恶化了，因为 PLL 对分频器产生在带内的噪声（小数分频杂散）是滤不掉的。于是就考虑到 SDM，因为 SDM 产生的也是伪随机数列，但它的频谱不是白的，而是高通的，这就恰到好处！因为 PLL 对 高频有抑制。结果就是：因为小数分频，动态改变分频比恶化了带内噪声，但是 SDM 有 整形效果，总算缓解了一些。
    参考文献 【1】 NI 小数分频锁相环的工作原理 【2】 ADI AN-282， AN-283 ，AN-388， AN-389， AN-1063 ，MT-022 【3】 Michael Henderson Perrott Techniques for High Data Rate Modulation and Low Power Operation of Fractional-N Frequency Synthesizers 【4】 王冲 一种新的实现 Σ-Δ 调制小数分频方案的研究 【5】 王家礼，孙璐 频率合成技术
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料