logo资料库

音乐合成实验报告.pdf

发布时间：2022-06-18 发布人：admin 分类：说明书 资料大小：1.00M 资料格式：pdf 举报 版权申诉
第1页 / 共24页
第2页 / 共24页
第3页 / 共24页
第4页 / 共24页
第5页 / 共24页
第6页 / 共24页
第7页 / 共24页
第8页 / 共24页
资料共24页，剩余部分请下载后查看
    音乐合成大作业 实验报告 无 84 王梦娣 2008011134
    音乐合成大作业实验报告 无 84 王梦娣 200811134 实验报告部分 一、 简单的音乐合成 1． 请根据《东方红》片断的简谱和“十二平均律”计算出该片断中各个乐音的频率，在 MATLAB 中生成幅度为 1 、抽样频率为 8kHz 的正弦信号表示这些乐音。请用 sound 函 数播放每个乐音，听一听音调是否正确。最后用这一系列乐音信号拼出《东方红》片断， 注意控制每个乐音持续的时间要符合节拍，用 sound 播放你合成的音乐，听起来感觉 如何？ 问题解答： 《东方红》片段： 其中所用音符的唱名、音名及对应频率（由十二平均律和相应键数间隔即可导 出）如下：（单位是 Hz） 5 5 6 2 1 1 6. 2 523.25 523.25 587.33 392 349.23 349.23 293.66 392 用 sound 播放单音，音调正确。以一拍 0.5 秒计，播出合成音乐。发现音乐听起来， 总体上音调、节拍正确，但乐音无声音强弱变化，两音之间有明显的“啪”的杂声。 2． 你一定注意到(1) 的乐曲中相邻乐音之间有“啪”的杂声，这是由于相位不连续产生了 高频分量。这种噪声严重影响合成音乐的质量，丧失真实感。为了消除它，我们可以用 图1.5 所示包络修正每个乐音，以保证在乐音的邻接处信号幅度为零。此外建议用指数 衰减的包络来表示。 问题解答： 这个问题，实际上我并没有完全理解题意，没有明白是需要乐音之间有重叠，还是 没有重叠，所以，我把两种方法都做了一遍，结果发现，用耳朵完全听不出区别。 2 / 24
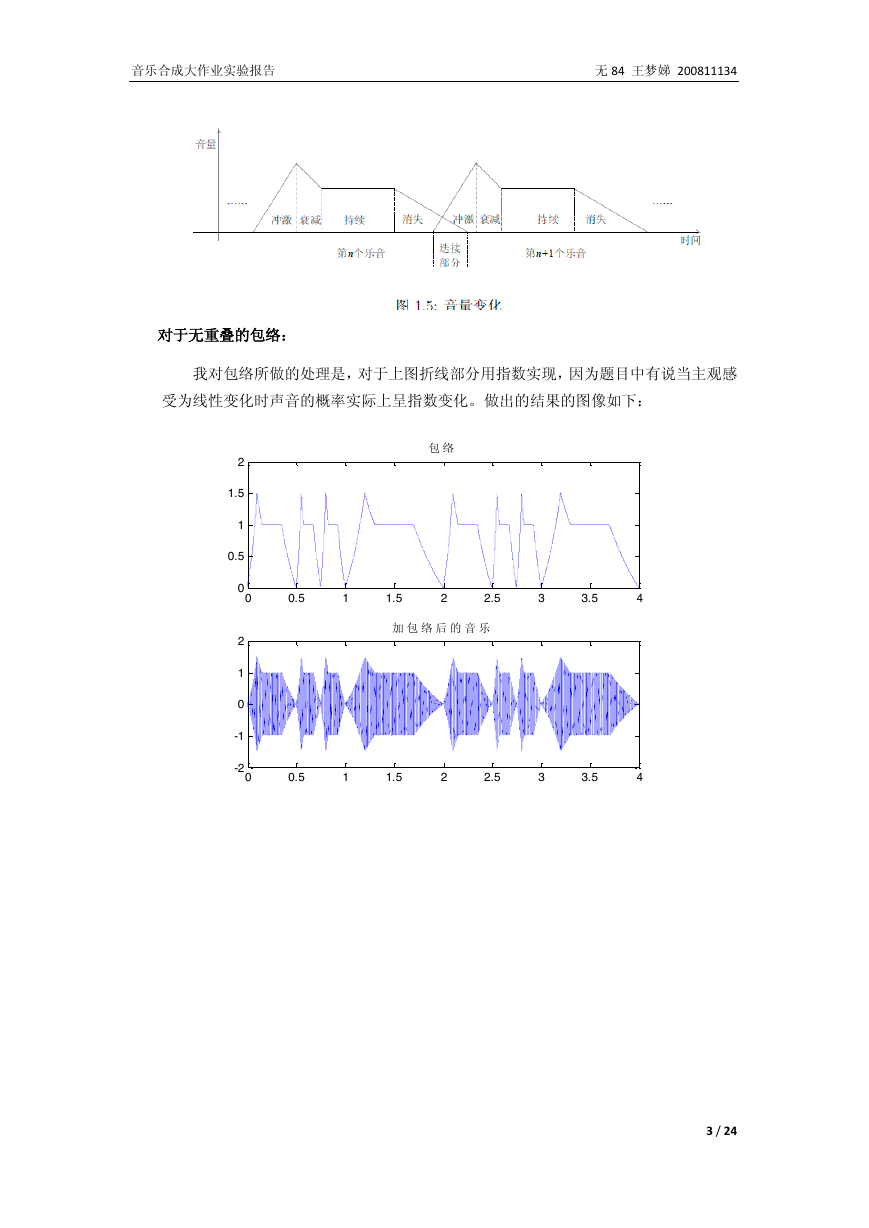
    音乐合成大作业实验报告 无 84 王梦娣 200811134 对于无重叠的包络： 我对包络所做的处理是，对于上图折线部分用指数实现，因为题目中有说当主观感 受为线性变化时声音的概率实际上呈指数变化。做出的结果的图像如下： 3 / 24 00.511.522.533.5400.511.52包络00.511.522.533.54-2-1012加包络后的音乐
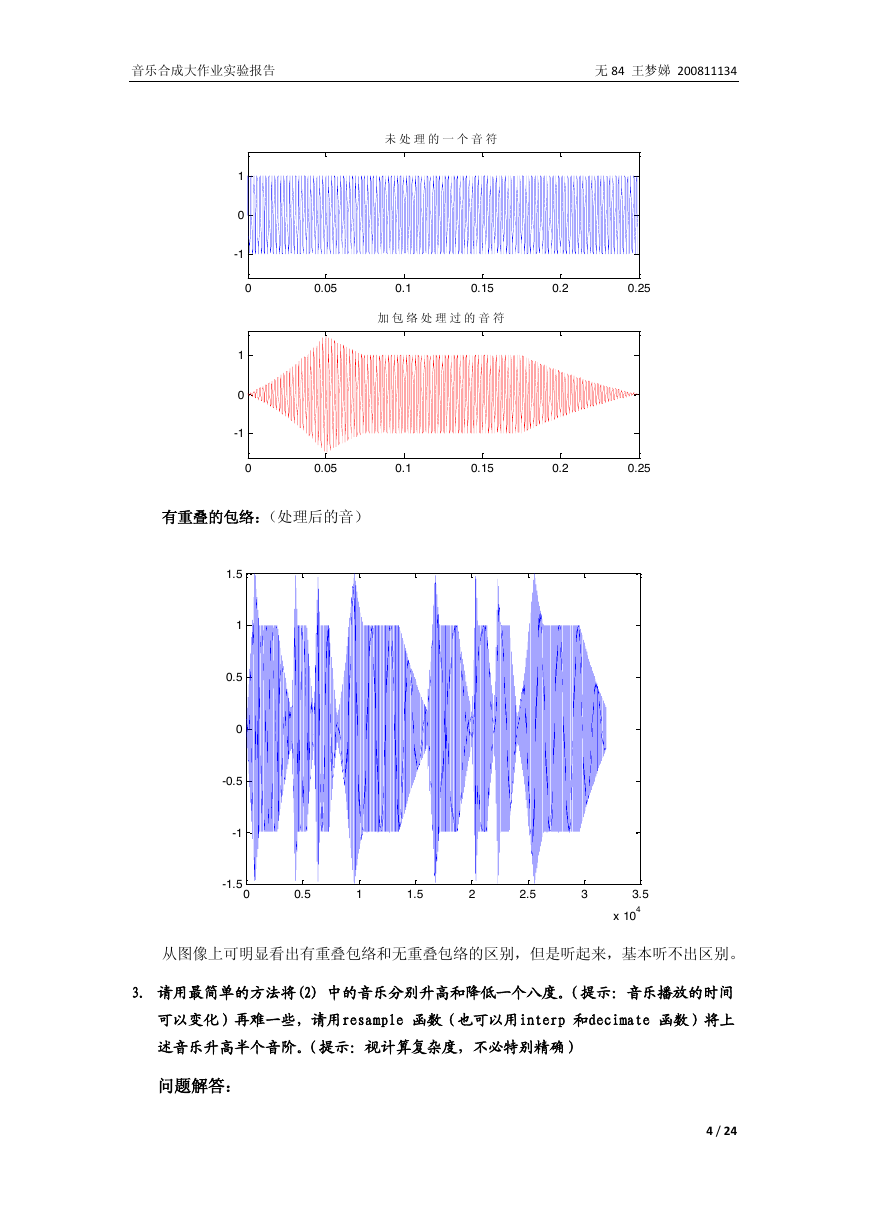
    音乐合成大作业实验报告 无 84 王梦娣 200811134 有重叠的包络：（处理后的音） 从图像上可明显看出有重叠包络和无重叠包络的区别，但是听起来，基本听不出区别。 3． 请用最简单的方法将(2) 中的音乐分别升高和降低一个八度。（提示：音乐播放的时间 可以变化）再难一些，请用resample 函数（也可以用interp 和decimate 函数）将上 述音乐升高半个音阶。（提示：视计算复杂度，不必特别精确） 问题解答： 4 / 24 00.050.10.150.20.25-101未处理的一个音符00.050.10.150.20.25-101加包络处理过的音符00.511.522.533.5x 104-1.5-1-0.500.511.5
    音乐合成大作业实验报告 无 84 王梦娣 200811134 由于题目中已有提示“音乐播放的时间可以变化”，所以很容易就想到用Sample函 数实现音调的改变，用Sample函数也确实是最简单的方法。 对于升高半个音阶，通过“十二平均律”的方法可知，所谓提高半个音阶，即频率提 高2^12≈1.06 倍。这也就可以运用resample函数用这个比例重新抽样，这里的关键就是 resample函数的应用。 4． 试着在(2) 的音乐中增加一些谐波分量，听一听音乐是否更有“厚度”了？注意谐波分 量的能量要小，否则掩盖住基音反而听不清音调了。（如果选择基波幅度为1 ，二次谐 波幅度0:2 ，三次谐波幅度0:3 ，听起来像不像象风琴？） 问题解答： 这里只需要改变各个音的组成，加上各次谐波即可。 5． 自选其他音乐合成，例如《贝多芬第五交响乐》的开头两小节。 问题解答： 这里的方法与前面完全相同，只是改变乐谱，映射到技术问题上就是改变基频。 二、 用傅里叶级数分析音乐 现在我们开始要处理真实的音乐信号了！请用load 命令载入附件光盘中的数据文件 \guitar.mat"，工作区会出现两个新的变量realwave 和wave2proc （可以用who 查看变量名）， 如图1.6 和1.7 所示。其中前者是从一段吉他乐曲（附件光盘上的\fmt.wav"）中截取下来的 真实信号，后者是用信号处理方法得到的这段信号的理论值，它们的抽样率都是8kHz。 5 / 24
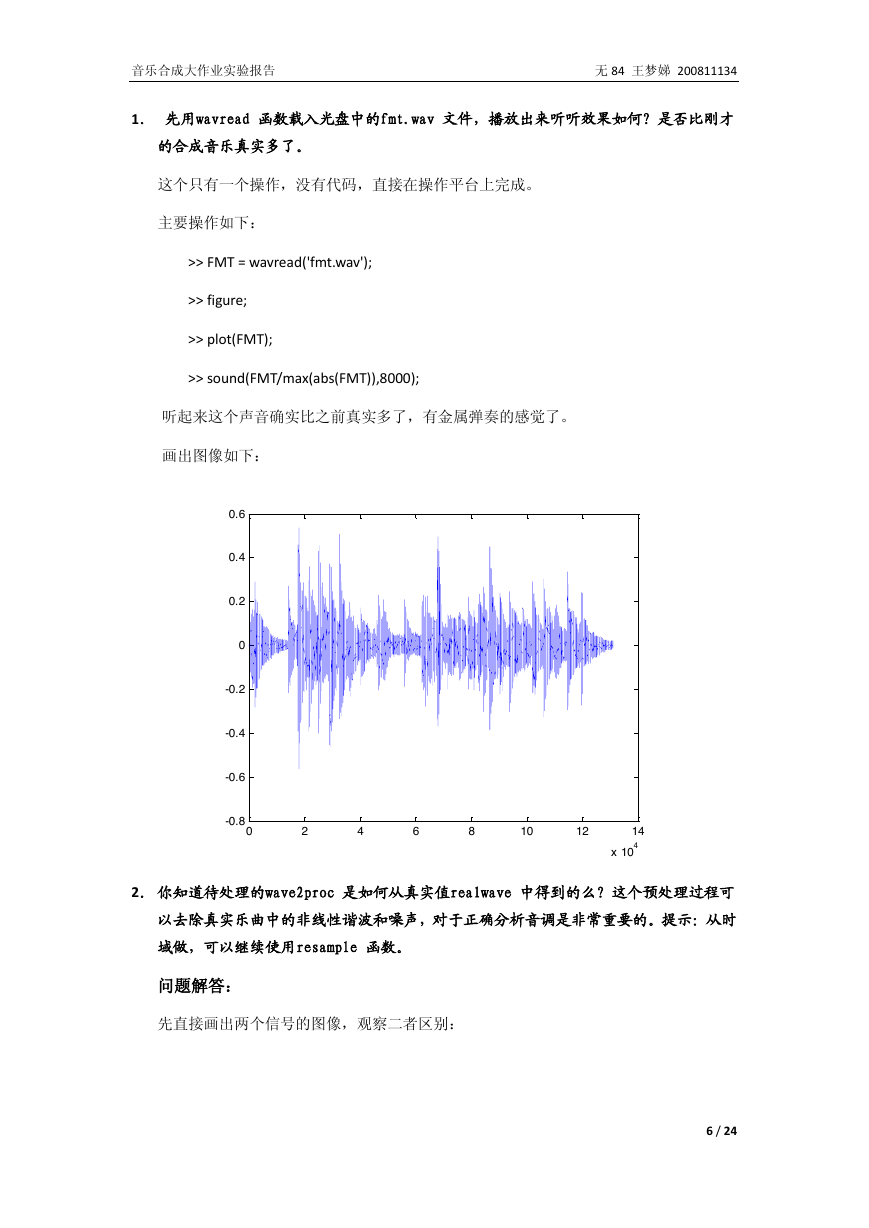
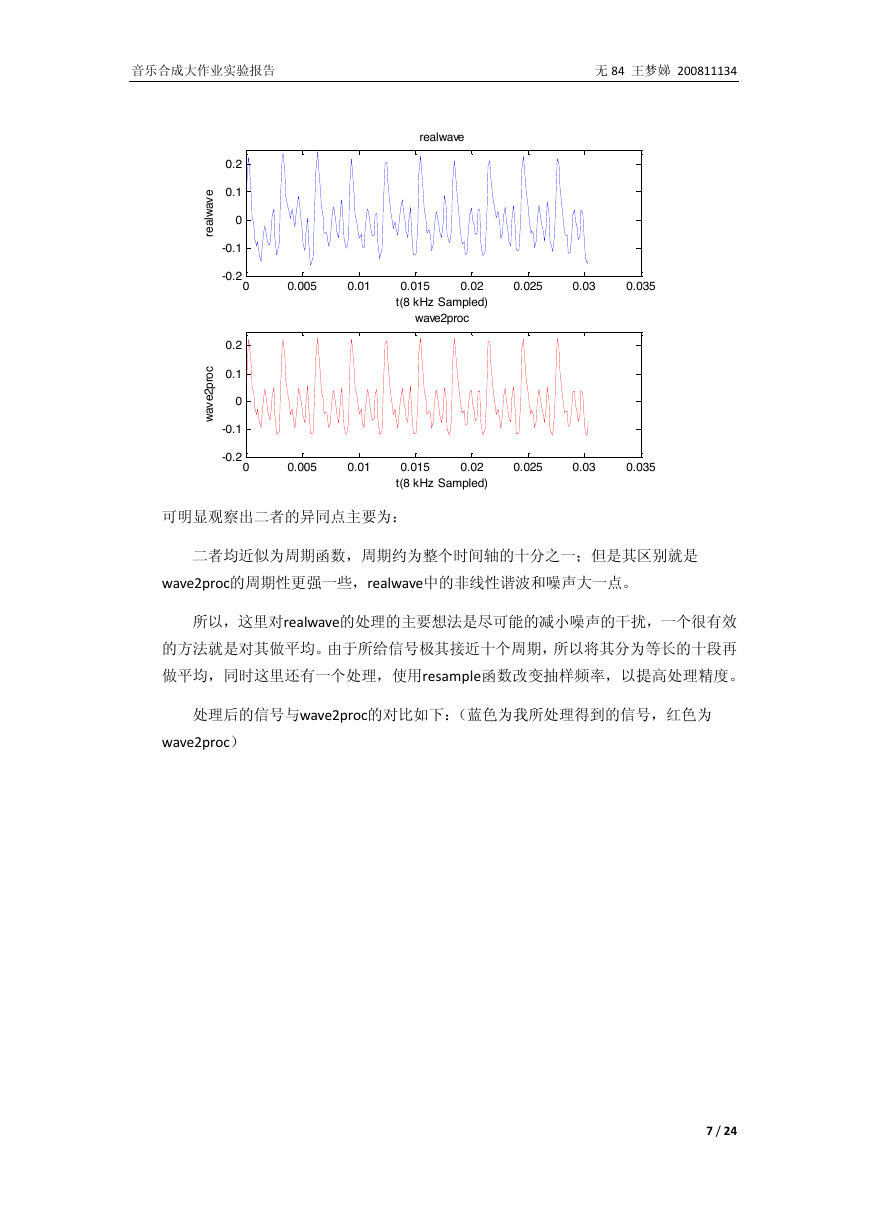
    音乐合成大作业实验报告 无 84 王梦娣 200811134 1． 先用wavread 函数载入光盘中的fmt.wav 文件，播放出来听听效果如何？是否比刚才 的合成音乐真实多了。 这个只有一个操作，没有代码，直接在操作平台上完成。 主要操作如下： >> FMT = wavread('fmt.wav'); >> figure; >> plot(FMT); >> sound(FMT/max(abs(FMT)),8000); 听起来这个声音确实比之前真实多了，有金属弹奏的感觉了。 画出图像如下： 2． 你知道待处理的wave2proc 是如何从真实值realwave 中得到的么？这个预处理过程可 以去除真实乐曲中的非线性谐波和噪声，对于正确分析音调是非常重要的。提示：从时 域做，可以继续使用resample 函数。 问题解答： 先直接画出两个信号的图像，观察二者区别： 6 / 24 02468101214x 104-0.8-0.6-0.4-0.200.20.40.6
    音乐合成大作业实验报告 无 84 王梦娣 200811134 可明显观察出二者的异同点主要为： 二者均近似为周期函数，周期约为整个时间轴的十分之一；但是其区别就是 wave2proc的周期性更强一些，realwave中的非线性谐波和噪声大一点。 所以，这里对realwave的处理的主要想法是尽可能的减小噪声的干扰，一个很有效 的方法就是对其做平均。由于所给信号极其接近十个周期，所以将其分为等长的十段再 做平均，同时这里还有一个处理，使用resample函数改变抽样频率，以提高处理精度。 处理后的信号与wave2proc的对比如下：（蓝色为我所处理得到的信号，红色为 wave2proc） 7 / 24 00.0050.010.0150.020.0250.030.035-0.2-0.100.10.2realwavet(8 kHz Sampled)realwave00.0050.010.0150.020.0250.030.035-0.2-0.100.10.2wave2proct(8 kHz Sampled)wave2proc
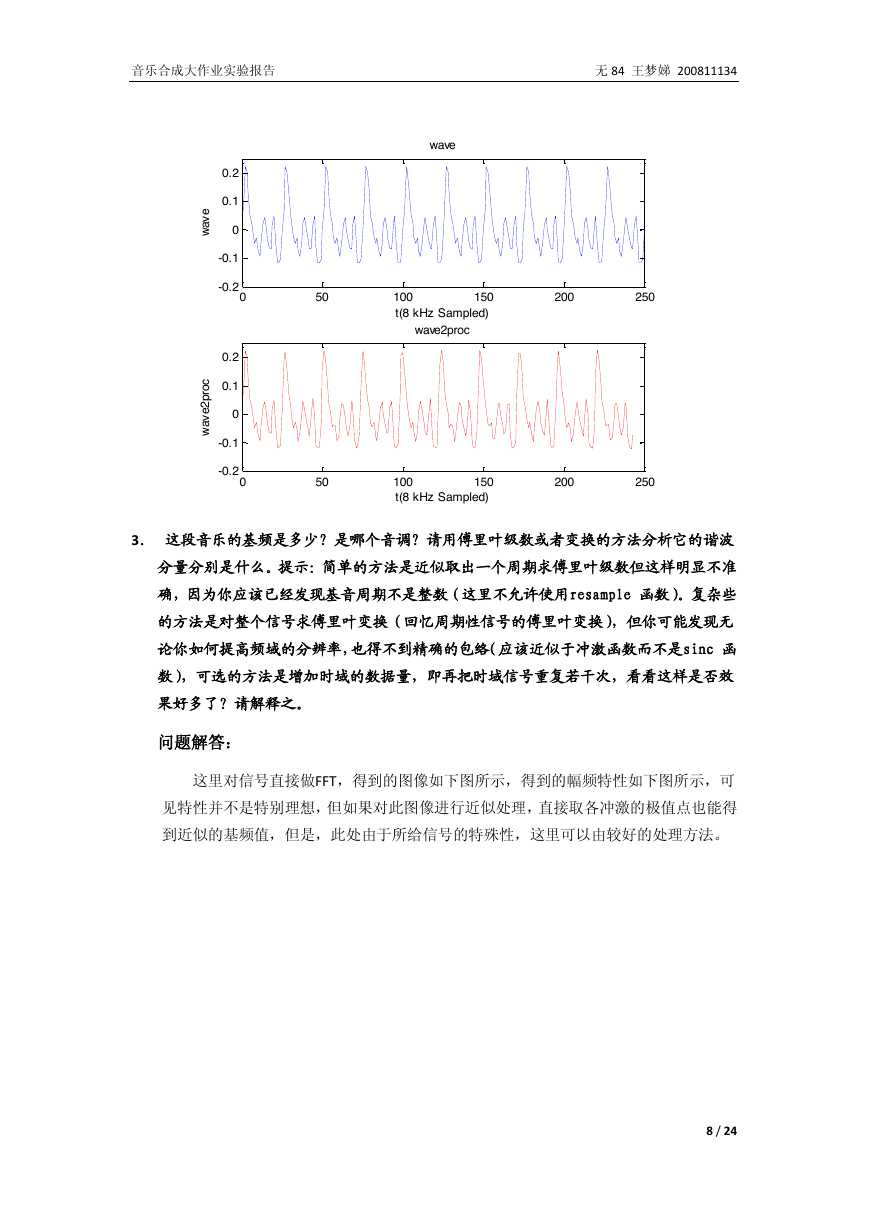
    音乐合成大作业实验报告 无 84 王梦娣 200811134 3． 这段音乐的基频是多少？是哪个音调？请用傅里叶级数或者变换的方法分析它的谐波 分量分别是什么。提示：简单的方法是近似取出一个周期求傅里叶级数但这样明显不准 确，因为你应该已经发现基音周期不是整数（这里不允许使用resample 函数）。复杂些 的方法是对整个信号求傅里叶变换（回忆周期性信号的傅里叶变换），但你可能发现无 论你如何提高频域的分辨率，也得不到精确的包络（应该近似于冲激函数而不是sinc 函 数），可选的方法是增加时域的数据量，即再把时域信号重复若干次，看看这样是否效 果好多了？请解释之。 问题解答： 这里对信号直接做FFT，得到的图像如下图所示，得到的幅频特性如下图所示，可 见特性并不是特别理想，但如果对此图像进行近似处理，直接取各冲激的极值点也能得 到近似的基频值，但是，此处由于所给信号的特殊性，这里可以由较好的处理方法。 8 / 24 050100150200250-0.2-0.100.10.2wavet(8 kHz Sampled)wave050100150200250-0.2-0.100.10.2wave2proct(8 kHz Sampled)wave2proc
    分享到：
    赞 收藏

    相关推荐

    资料库

    信息化

    共收录1827份资料，累计6个分类，关注成员有19位，主要包括：管理软件,企业管理,电子商务,其它,IT管理,项目管理

    热门标签

    管理软件 企业管理 电子商务 其它 IT管理 项目管理

    最新资料