logo资料库

主成分分析介绍及实例.doc

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：0.10M 资料格式：doc 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    第四节 主成分分析方法 地理环境是多要素的复杂系统，在我们进行地理系统分析时，多变量问题 是经常会遇到的。变量太多，无疑会增加分析问题的难度与复杂性，而且在许多 实际问题中，多个变量之间是具有一定的相关关系的。因此，我们就会很自然地 想到，能否在各个变量之间相关关系研究的基础上，用较少的新变量代替原来较 多的变量，而且使这些较少的新变量尽可能多地保留原来较多的变量所反映的信 息？事实上，这种想法是可以实现的，本节拟介绍的主成分分析方法就是综合处 理这种问题的一种强有力的方法。 第一节 主成分分析方法的原理 主成分分析是把原来多个变量化为少数几个综合指标的一种统计分析方法， 从数学角度来看，这是一种降维处理技术。假定有 n 个地理样本，每个样本共有 p 个变量描述，这样就构成了一个 n×p 阶的地理数据矩阵： 如何从这么多变量的数据中抓住地理事物的内在规律性呢？要解决这一问 题，自然要在 p 维空间中加以考察，这是比较麻烦的。为了克服这一困难，就需 要进行降维处理，即用较少的几个综合指标来代替原来较多的变量指标，而且使 这些较少的综合指标既能尽量多地反映原来较多指标所反映的信息，同时它们之 间又是彼此独立的。那么，这些综合指标（即新变量)应如何选取呢？显然，其 最简单的形式就是取原来变量指标的线性组合，适当调整组合系数，使新的变量 指标之间相互独立且代表性最好。 如果记原来的变量指标为 x1，x2，…，xp，它们的综合指标——新变量指标 为 x1，x2，…，zm（m≤p)。则
    在（2)式中，系数 lij由下列原则来决定： （1)zi与 zj（i≠j；i，j=1，2，…，m)相互无关； （2)z1是 x1，x2，…，xp的一切线性组合中方差最大者；z2是与 z1 不相关的 x1，x2，…，xp 的所有线性组合中方差最大者；……；zm是与 z1，z2，……zm-1都不 相关的 x1，x2，…，xp的所有线性组合中方差最大者。 这样决定的新变量指标 z1，z2，…，zm 分别称为原变量指标 x1，x2，…，xp 的第一，第二，…，第 m 主成分。其中，z1在总方差中占的比例最大，z2，z3，…， zm的方差依次递减。在实际问题的分析中，常挑选前几个最大的主成分，这样既 减少了变量的数目，又抓住了主要矛盾，简化了变量之间的关系。 从以上分析可以看出，找主成分就是确定原来变量 xj（j=1，2，…，p)在诸 主成分 zi（i=1，2，…，m)上的载荷 lij（i=1，2，…，m；j=1，2，…，p)，从 数学上容易知道，它们分别是 x1，x2，…，xp的相关矩阵的 m 个较大的特征值所 对应的特征向量。 第二节 主成分分析的解法 主成分分析的计算步骤 通过上述主成分分析的基本原理的介绍，我们可以把主成分分析计算步骤归 纳如下： （1)计算相关系数矩阵 在公式（3)中，rij（i，j=1，2，…，p)为原来变量 xi与 xj的相关系数，其 计算公式为 因为 R 是实对称矩阵（即 rij=rji)，所以只需计算其上三角元素或下三角元素 即可。 （2)计算特征值与特征向量
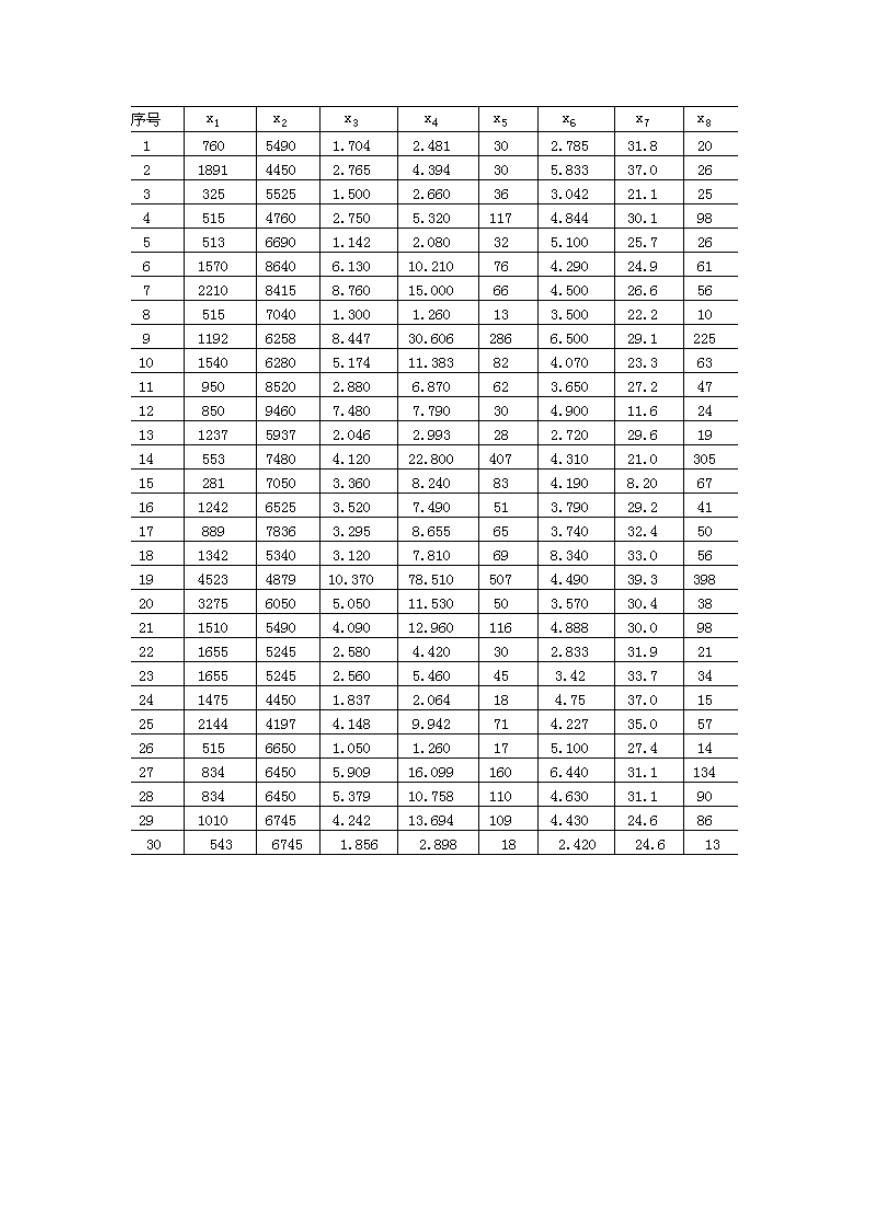
    首先解特征方程｜λI-R｜=0 求出特征值λi（i=1，2，…，p)，并使其按大 小顺序排列，即λ1≥λ2≥…，≥λp≥0；然后分别求出对应于特征值λi 的特征 向量 ei（i=1，2，…，p)。 （3)计算主成分贡献率及累计贡献率 一般取累计贡献率达 85-95％的特征值λ1，λ2，…，λm 所对应的第一，第 二，……，第 m（m≤p)个主成分。 （4)计算主成分载荷 由此可以进一步计算主成分得分： 第三节 主成分分析应用实例 主成分分析实例 对于某区域地貌-水文系统，其 57 个流域盆地的九项地理要素：x1为流域盆 地总高度（m)x2为流域盆地山口的海拔高度（m)，x3为流域盆地周长（m)，x4 为 河道总长度（km)，x5为河 表 2-14 某 57 个流域盆地地理要素数据
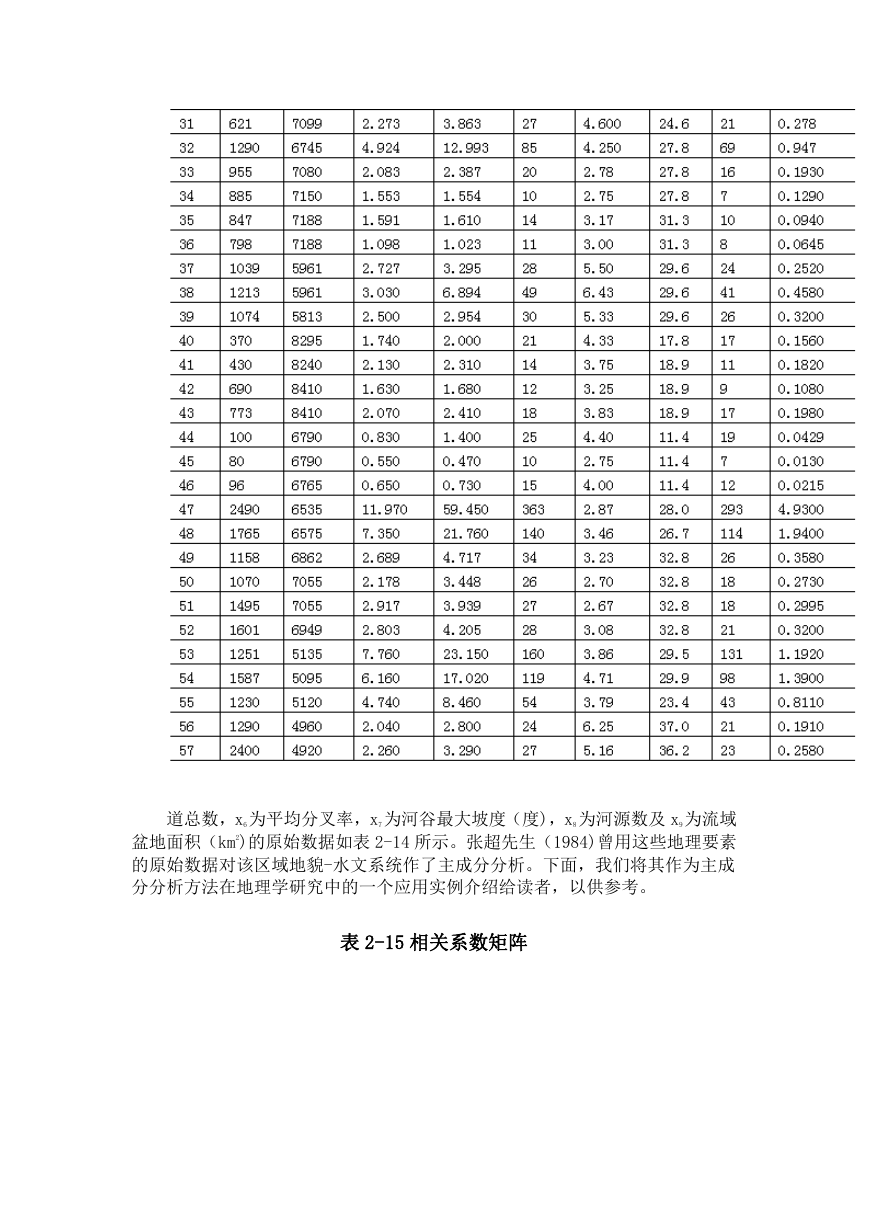
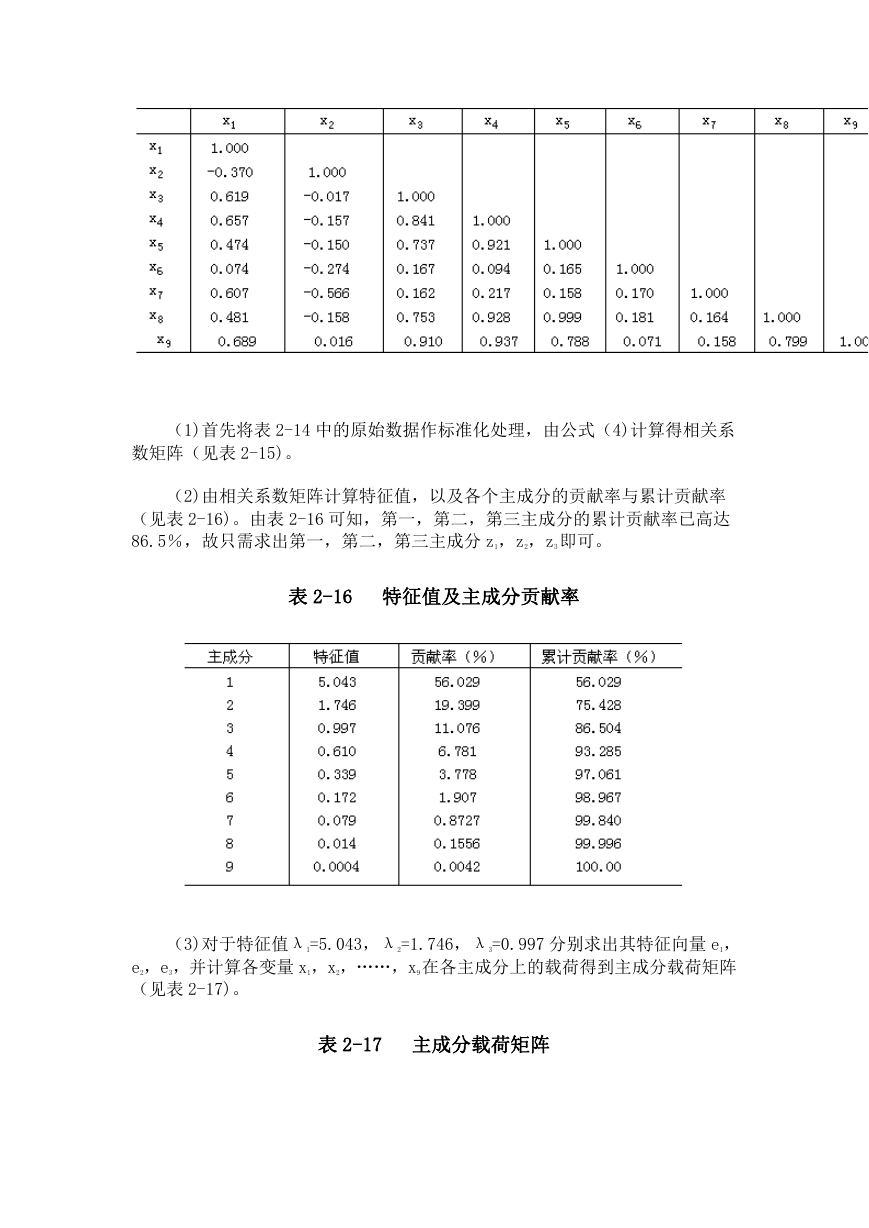
    道总数，x6为平均分叉率，x7为河谷最大坡度（度)，x8 为河源数及 x9为流域 盆地面积（km2)的原始数据如表 2-14 所示。张超先生（1984)曾用这些地理要素 的原始数据对该区域地貌-水文系统作了主成分分析。下面，我们将其作为主成 分分析方法在地理学研究中的一个应用实例介绍给读者，以供参考。 表 2-15 相关系数矩阵
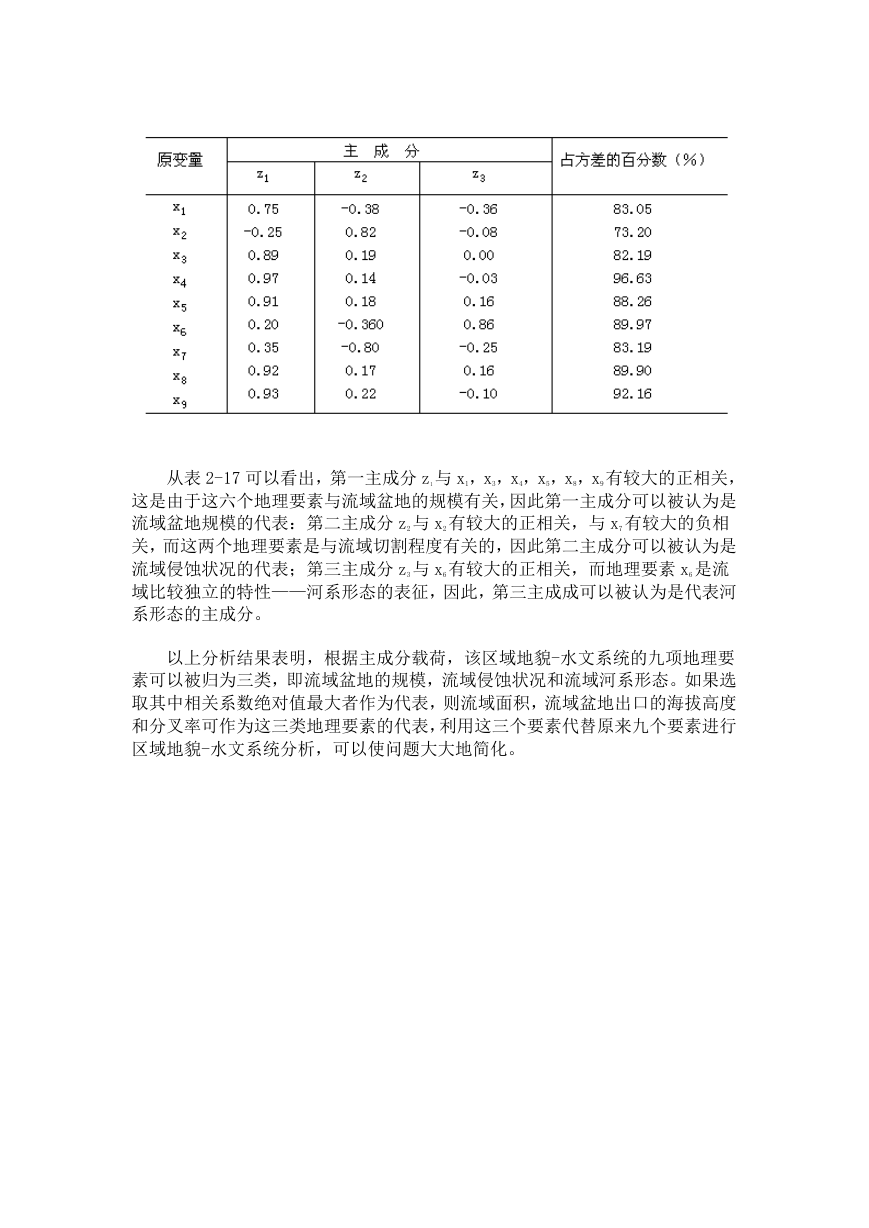
    （1)首先将表 2-14 中的原始数据作标准化处理，由公式（4)计算得相关系 数矩阵（见表 2-15)。 （2)由相关系数矩阵计算特征值，以及各个主成分的贡献率与累计贡献率 （见表 2-16)。由表 2-16 可知，第一，第二，第三主成分的累计贡献率已高达 86.5％，故只需求出第一，第二，第三主成分 z1，z2，z3即可。 表 2-16 特征值及主成分贡献率 （3)对于特征值λ1=5.043，λ2=1.746，λ3=0.997 分别求出其特征向量 e1， e2，e3，并计算各变量 x1，x2，……，x9在各主成分上的载荷得到主成分载荷矩阵 （见表 2-17)。 表 2-17 主成分载荷矩阵
    从表 2-17 可以看出，第一主成分 z1与 x1，x3，x4，x5，x8，x9有较大的正相关， 这是由于这六个地理要素与流域盆地的规模有关，因此第一主成分可以被认为是 流域盆地规模的代表：第二主成分 z2与 x2有较大的正相关，与 x7 有较大的负相 关，而这两个地理要素是与流域切割程度有关的，因此第二主成分可以被认为是 流域侵蚀状况的代表；第三主成分 z3与 x6有较大的正相关，而地理要素 x6 是流 域比较独立的特性——河系形态的表征，因此，第三主成成可以被认为是代表河 系形态的主成分。 以上分析结果表明，根据主成分载荷，该区域地貌-水文系统的九项地理要 素可以被归为三类，即流域盆地的规模，流域侵蚀状况和流域河系形态。如果选 取其中相关系数绝对值最大者作为代表，则流域面积，流域盆地出口的海拔高度 和分叉率可作为这三类地理要素的代表，利用这三个要素代替原来九个要素进行 区域地貌-水文系统分析，可以使问题大大地简化。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料