第1页 / 共16页
第2页 / 共16页
第3页 / 共16页
第4页 / 共16页
第5页 / 共16页
第6页 / 共16页
第7页 / 共16页
第8页 / 共16页
LNV和LFV半轻子衰变中的干扰效应：马约拉纳假说.pdf
Introduction
Semileptonic meson decays with two sterile neutrinos
Exploring the interference effect
Illustrative case: semileptonic kaon decays
Conclusions
Published for SISSA by
Springer
Received: April 29, 2019
Revised: July 18, 2019
Accepted: August 18, 2019
Published: September 3, 2019
Interference eects in LNV and LFV semileptonic
decays: the Majorana hypothesis
A. Abada,a C. Hati,b X. Marcanoa and A.M. Teixeirab
aLaboratoire de Physique Theorique, CNRS,
Univ. Paris-Sud, Universite Paris-Saclay, 91405 Orsay, France
bLaboratoire de Physique de Clermont (UMR 6533), CNRS/IN2P3,
Univ. Clermont Auvergne, 4 Av. Blaise Pascal, F-63178 Aubiere Cedex, France
E-mail: asmaa.abada@th.u-psud.fr, chandan.hati@clermont.in2p3.fr,
xabier.marcano@th.u-psud.fr, ana.teixeira@clermont.in2p3.fr
Abstract: In the case where the Standard Model is extended by one heavy Majorana
fermion, the branching fractions of semileptonic meson decays into same-sign and opposite-
sign dileptons are expected to be of the same order. As we discuss here, this need not be
the case in extensions by at least two sterile fermions, due to the possible destructive and
constructive interferences that might arise. Depending on the CP violating phases, one can
have an enhancement of the lepton number violating modes and suppression of the lepton
number conserving ones (and vice-versa). We explore for the rst time the interference
eects in semileptonic decays, and illustrate them for a future observation of kaon decays
at NA62. We also argue that a non-observation of a given mode need not be interpreted in
terms of reduced active-sterile mixings, but that it could instead be understood in terms of
interference eects due to the presence of several sterile states; in particular, for dierent-
avour nal state charged leptons, observing a lepton number conserving process and not
a lepton number violating one does not rule out that the mediators are Majorana fermions.
Keywords: Beyond Standard Model, CP violation, Kaon Physics, Neutrino Physics
ArXiv ePrint: 1904.05367
Open Access, c The Authors.
Article funded by SCOAP3.
https://doi.org/10.1007/JHEP09(2019)017
JHEP09(2019)017
Contents
1 Introduction
2 Semileptonic meson decays with two sterile neutrinos
3 Exploring the interference eect
4 Illustrative case: semileptonic kaon decays
5 Conclusions
1
3
5
8
13
1
Introduction
Several extensions of the Standard Model (SM) aiming at explaining oscillation phenomena
call upon the introduction of right-handed (RH) neutrinos, and the embedding of the seesaw
mechanism onto the SM is one of the most economical mechanisms for the generation of
neutrino masses and lepton mixings. The presence of relatively light RH neutrinos (sterile
fermions from the gauge point of view), which have non-negligible mixings with the active
ones, leads to the modication of the charged and neutral lepton currents, and thus the new
states can give rise to contributions to many observables, ranging from rare transitions and
decays at high-intensities to signals at colliders. Mechanisms of neutrino mass generation
relying on such sterile fermions are thus particularly appealing, as they oer the possibility
of being (albeit indirectly) tested.
The observation of a lepton number violating (LNV) processes signals the existence
of New Physics (NP) and is evidence of the Majorana nature of the exchanged fermions.
Lepton number violating meson and tau semileptonic decays are examples of such observ-
ables; currently, they are the object of extensive world-wide searches, for instance of NA62
(for the light mesons), BES-III for charmed mesons, and LHCb and Belle II for B-mesons
and tau leptons.
‘
2 , and ! ‘
M
1 ! ‘
‘
In this work we address the LNV meson and tau lepton semileptonic three-body decays,
M
M
1 ! ‘
2 , as well as their lepton number conserving (LNC)
counterparts, M
(with the dierent mesonic states
M1;2 and charged lepton avours and including all kinematically allowed possiblities).
When mediated by sterile fermions, the joint study of the LNC and LNV processes allows
to shed light on the nature (Dirac or Majorana) of the exchanged mediator.
M
2 , and ! ‘
1 M
1 M
M
2
In the presence of Majorana heavy neutral leptons (a right-handed neutrino, or other
sterile fermions), one can have sizeable branching fractions (BRs) for lepton number vio-
lating processes, when the Majorana states are produced on-shell [1{11] | the so-called
\resonant production" regime.
In the case in which a single sterile fermion is present,
{ 1 {
JHEP09(2019)017
the branching fractions for the semileptonic decays leading to same-sign and opposite-sign
dileptons are predicted to be of the same order. Notice that due to the existence of a single
heavy fermion, the decay widths are not sensitive to the latter’s CP Majorana phases | in
particular, one can still have contributions to LNV decays even if all Majorana CP phases
are set to zero. Interestingly, should more than one heavy Majorana state be present, the
relative size of the LNV and LNC channels may be very dierent due to interference eects
associated with the Dirac and Majorana phases.
In this work, we consider the SM extended by two sterile fermion states which mix with
the three active neutrinos; we take the neutrino mass eigenvalues and the lepton mixing
matrix to be independent, implying that no assumption is made on the actual mechanism of
neutrino mass generation, other than calling upon the presence of additional heavy singlets.
This set-up is useful to understand the general phenomenology of a broad class of models
where the SM is enlarged only by sterile fermions, such as the type-I seesaw mechanism
and its variants. Other than being in the mass range to be produced \on-shell" in the
semileptonic decays, the two new states are taken to be suciently close in mass to allow
for sizeable interference eects (constructive or destructive) in the LNV and LNC decays,
in association with the new CP -violating phases.
As we will discuss in detail, depending on the sterile fermion parameter space (i.e.,
their masses, mass dierence and mixings to the active neutrinos | including the CP
violating phases), the interference eects can lead to various scenarios, ranging from an
extreme suppression of the lepton number conserving observables while having large con-
tributions to lepton number violating ones (and this contrary to the usual belief), to the
reverse case. Our ndings, relying on a complete numerical analysis, strongly suggest that
eects leading to suppressions in some channels should be taken into account upon the
interpretation of a non-observation of LNV or LNC meson (or tau) semileptonic decays:
reduced BRs might result from the interference of (at least) two sterile states with small
mass dierence(s), and should not be necessarily translated into more stringent bounds on
the heavy neutrino couplings to the active ones. More importantly, the observation of a
lepton number conserving process accompanied by negative search results for the corre-
sponding LNV modes (with both predicted to be within experimental sensitivity) does not
necessarily imply that the mediators are of Dirac nature.
Here we present the results of our study, focusing on the semileptonic kaon decays
currently searched for in NA62, that is K ! ‘
decays and the corresponding lepton
number conserving ones, K ! ‘
(where ; denote electrons and/or muons). Kaon
decays are used here as an illustrative example, as the results generically hold for all similar
semileptonic decays (including tau decays).
‘
‘
Similar studies have focused on the prospects of LNV searches at colliders, see [12],
and references therein. Some works have explored the role of the second heavy neutrino
concerning the possibility of resonant CP violation [13], in a forward-backward asymmetry
at electron-positron collider [14], while others have compared the expected number of events
associated with same-sign and opposite-sign dileptons at colliders in the framework of Left-
{ 2 {
JHEP09(2019)017
Right symmetric models1 [16]. The latter analysis considered scenarios in which the relative
CP violating phases of active-sterile mixings were identical for the heavy neutrinos. In our
work | aiming at studying rare meson decays at lower energies | we relax this restrictive
hypothesis, which opens the possibility of very distinct behaviours for the LNV and LNC
rates, due to the interference eects.
Although the study is carried for a simplied SM extension (the \3+2" minimal model),
we emphasise that our results generically apply to complete mechanisms of neutrino mass
generation, provided at least two additional states are present, as in the case of low-scale
type I seesaw frameworks (in which at least two RH neutrinos are required to accommodate
oscillation data).
This work is organised as follows: after an analytical discussion in section 2 of semilep-
tonic meson decay LNC and LNV amplitudes (in the presence of two additional sterile
states), we explore in section 3 the interference eects in a generic way, identifying criti-
cal regimes and the potential consequences for the relative size of the BRs. Section 4 is
dedicated to a full numerical analysis, in which the intereference eects are illustrated for
kaon decays. We discuss further points, and summarise our most important ndings in
the conclusions.
2 Semileptonic meson decays with two sterile neutrinos
As stated in the Introduction, we work in the framework of simplied SM extensions via the
addition of N extra neutral Majorana fermions, making no assumption on the mechanism
of neutrino mass generation (i.e., considering neutrino masses and lepton mixings to be
independent).
In the presence of new sterile states with non-negligible mixings to the
(light) active neutrinos, the leptonic charged current is modied as
Lcc =
gp
2
Ui ‘ PL i W
+ H.c. ;
(2.1)
in which i denotes the physical neutrino states, from 1 to 3 + N , and the avour of
the charged leptons. For the case N = 2 (corresponding to the addition of two states
with masses m4;5), the unitary matrix U , which encodes avour mixing in charged current
interactions, can be parametrised in terms of ten rotation matrices and 4 additional phases
as follows [17, 18]
U = R45 R35 R25 R15 R34 R24 R14 R23 R13 R12 diag1; ei’2; ei’3; ei’4; ei’5 :
(2.2)
In the above, Rij corresponds to the rotation matrix between the i and j states (each
parametrised by a mixing angle ij and a CP -violating phase ij). For instance, the
rotation matrix R14 can be explicitly cast as
(2.3)
0BBBBB@
R14 =
1See also the recent work [15].
cos 14
0 0 sin 14 ei14 0
0
1 0
0
0 1
sin 14 ei14 0 0
0
1
0 0
cos 14
0
0
0
0
0
0
1CCCCCA ;
{ 3 {
JHEP09(2019)017
and similarly for the other Rij. We refer to ij and ’i respectively as Dirac and Majorana
phases since, as we will see later, the ’i phases will only appear in LNV processes, while
the ij will aect both LNV and LNC processes. Notice that for the considered set-up
(adding only SM singlet fermions) not all the mixings and phases are physical and some of
them could be removed [19]; for the forthcoming discussion, only the mixings of the sterile
states to the active sector are relevant and constitute, therefore, our input parameters. We
denote them by
Following eq. (2.2), these mixings can be expressed as
Ui = eiijUij; = e; ; ; and i = 4; 5 :
0B@ Ue4 Ue5
1CA
0B@ s14ei(41’4) s15ei(51’5)
1CA ;
U4 U5
U 4 U 5
s24ei(42’4) s25ei(52’5)
s34ei(43’4) s35ei(53’5)
where sij = sin ij and where we have neglected terms of O(s2
analysis, we will nevertheless use the generic notation of eq. (2.4).
ij). For the rest of the
We now address the eect of the new mixings on the LNC semileptonic processes M !
‘
and the corresponding LNV ones M ! M0‘
M0‘
, M and M0 being pseudoscalar
mesons2. Their squared amplitudes (see [11]) are proportional, up to overall constant
parameters, to the following:
‘
(2.4)
(2.5)
M!M0‘+
‘
M!M0‘
M!M0‘+
M!M0‘
‘
ALNC
ALNC
ALNV
ALNV
ALNC
ALNV
M!M0‘
‘
M!M0‘
‘
;
;
‘+
‘+
5g(m5)
5U5g(m5)
4U4g(m4) + U
4g(m4) + U5U
2 /U4U
2
2 /U
2
2 /U4U4f (m4) + U5U5f (m5)
2
2 /U
2
2/U4
2jg(M )j21 + 0 ei( )2
2U4
2/U4
2jf (M )j21 + ei( + )2
2U4
4f (m4) + U
5f (m5)
4U
5U
;
;
;
;
(2.6)
(2.7)
leading to
where we have dened 5 4, and M is the average mass of the two sterile
neutrinos (M their mass splitting), so that m4 = M M=2 and m5 = M + M=2. The
functions f and g are the integrals one obtains when computing the decay amplitudes for
LNV and LNC semileptonic decays of mesons (details can be found in for instance [11]).
2Here we present the case of semileptonic meson decays; however, a similar discussion holds for semilep-
and
tonic tau decays ! M M0‘, = e; . Moreover, for simplicity we focus on M + ! M
M + ! M
0+‘+
‘
0‘+
‘+
.
{ 4 {
JHEP09(2019)017
The complex quantities and 0, which reect the relative size of the contributions of the
two sterile fermions to the processes, are dened as
jU5U5j
jU4U4j
f (m5)
f (m4)
;
0 jU5U
5j
jU4U
4j
g(m5)
g(m4)
:
(2.8)
Equations (2.6), (2.7) allow to infer several important points: the LNC decay ampli-
tudes are not sensitive to the CP violating phases ’i, as these cancel out in the
combination, therefore revealing their Majorana nature; the LNC decay amplitudes are
sensitive to the ij (Dirac) phases, but only in the case of avour violating nal states, i.e.
6= [13]. On the other hand, the LNV decay amplitudes are sensitive to both Dirac and
Majorana CP phases (since the phase appearing in the decay amplitude is the sum of the
relative CP phases, + ), and this even in the case of identical charged leptons in the
nal state ( = ).
In order to discuss the impact of the CP phases on the LNV and LNC decay ampli-
tudes, as well as possible interference eects, we consider the quantity R‘‘ dened as
R‘‘ LNV
M!M0‘
LNC
M!M0‘
‘
‘
and further introduce the ratio eR‘‘
eR‘‘ LNC
;
(2.9)
1 R‘‘
1 + R‘‘
;
=
(2.10)
M!M0‘
LNV
+ LNV
‘
‘
M!M0‘
M!M0‘
LNC
M!M0‘
‘
‘
LNC
M!M0‘
with, in both ratios, LNC
, in the case in which 6= .
The ratio R‘‘ is usually considered to compare LNV to LNC processes (a similar
approach to what was done, for instance, in the context of collider searches [16]) and
the second ratio, eR‘‘ , which a priori might seem redundant, will be useful to better
M!M0‘
+ LNC
M!M0‘+
‘
‘
‘+
understand interference eects.
3 Exploring the interference eect
As extensively discussed in [1{11], in addition to being of Majorana nature, the sterile
fermions mediating the LNV decays should be produced on-shell, in which case one can
have a resonant enhancement of the decay widths. In the narrow-width approximation, this
\resonant enhancement" can be understood as an increase of O(mi=Ni) in the decay rates
(Ni denoting the width of the heavy sterile state Ni). For this reason, we will assume that
the individual widths are very small compared to the sterile neutrino masses,3 Ni mi.
In the case of the SM extended by only one heavy Majorana neutrino, we have veried
that the predictions for the LNV and LNC decay widths are of the same order, implying
3Notice that this assumption is well justied, as this is usually the case in seesaw-like models where the
sterile neutrinos are lighter than the typical meson masses [20].
{ 5 {
JHEP09(2019)017
that R‘‘ = 1 and thus eR‘‘ = 0. In the presence of two (or more) sterile fermions with
previous predictions for R and eR. However, when the mass splitting of the heavy Majorana
(clearly) non-degenerate masses, interference eects are negligible and one recovers the
states is very small, one can have an overlap between their contributions, possibly leading
to destructive or constructive interferences. The eect of the overlap will be maximal
should the mass splitting be even smaller than the Majorana neutrino decay widths. In
turn, this will lead to dierent predictions for the LNV and LNC decay widths, changing
the values R and eR. In summary, interference eects are expected to be relevant if both
the following conditions are realised:
M M and M < N ;
(3.1)
in which, for simplicity, we have assumed the widths to be the same N4 = N5 = N .
With these conditions, and in terms of the CP -violating phases, the ratio R‘‘ is given
as follows
(1 jj)2 + 4jj cos2 ( + )
(1 j0j)2 + 4j0j cos2 0( )
;
2
2
R‘‘ =
where we have set (0) = j(0)jei(0), and with the referring to the electric charge of the
lepton .
Moreover, the coecients and 0 of eq. (2.8) can be expanded as follows
In order to have sizeable interference eects, in addition to having a small mass splitting,
the relative size of the contributions of the two neutrinos to each amplitude should be
of the same order, and not very dierent from 1, jj j0j 1 (as can be seen from
eqs. (2.6), (2.7)), implying that the two neutrinos should mix with similar strength to the
relevant active avours.
Under the hypotheses of eq. (3.1), and in the limit jj j0j 1, one can derive the
ratios R‘‘ and eR‘‘ in terms of the CP -violating phases as
2 ( + )
2 ( ) ;
cos2 1
cos2 1
R‘‘ =
eR‘‘ =
sin sin
cos cos + 1
;
where (for simplicity) we have assumed in the last equations that = 0 = 0. One can
immediately notice from eq. (3.4) that, for 6= , the ratio R‘‘ can deviate from 1 (larger
or smaller) due to the presence of both relative CP violating phases, and .
The eect of the interference between the two sterile fermion contributions can already
be seen in the simple limiting case in which the relative CP -violating phases are identical
= (the same limit was also used in [16] regarding collider searches). This situation
can be realised if, for example, one sets all the Dirac CP phases to zero so that the ratio
{ 6 {
jj ’ j0j =
jU5U
5j
jU4U
4j
1 + O
M
N
:
(3.3)
(3.2)
(3.4)
(3.5)
JHEP09(2019)017
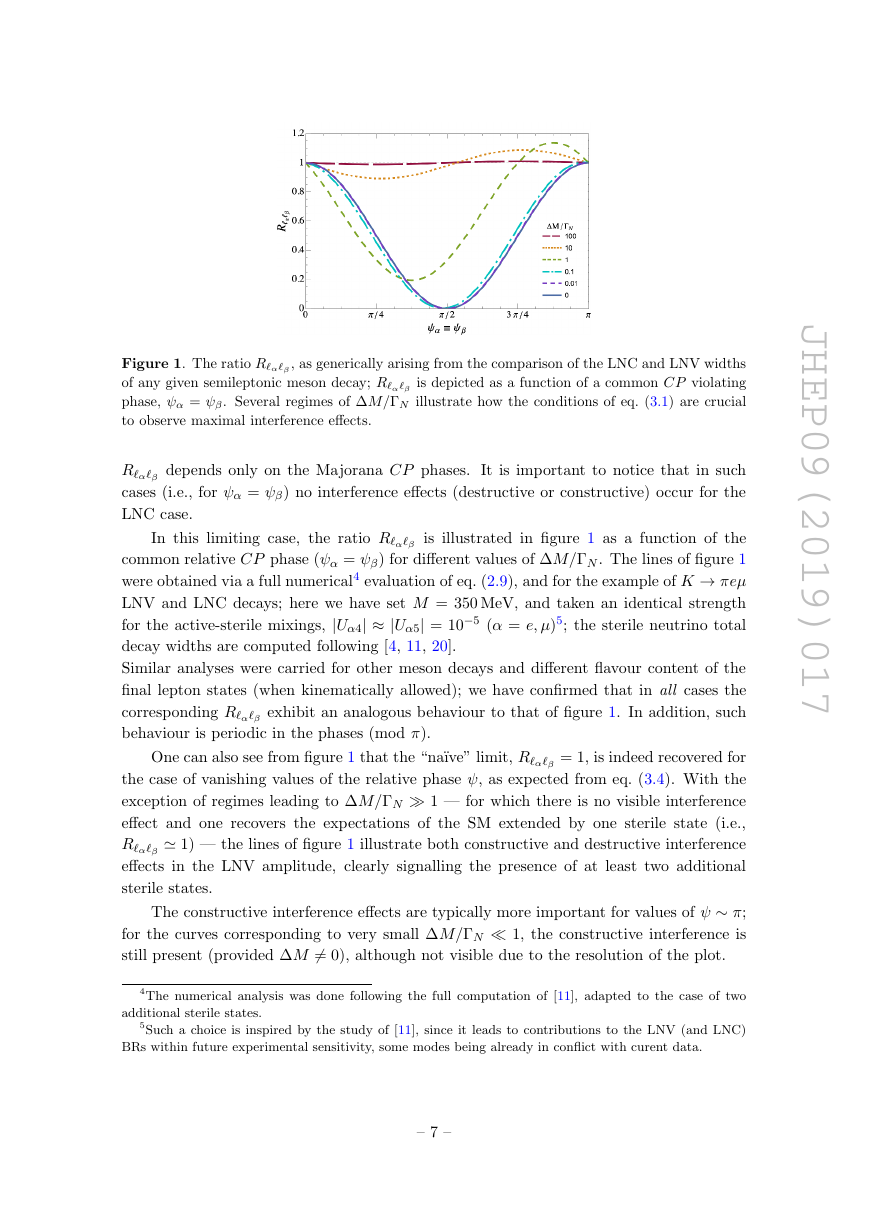
Figure 1. The ratio R‘‘ , as generically arising from the comparison of the LNC and LNV widths
of any given semileptonic meson decay; R‘‘ is depicted as a function of a common CP violating
phase, = . Several regimes of M=N illustrate how the conditions of eq. (3.1) are crucial
to observe maximal interference eects.
R‘‘ depends only on the Majorana CP phases. It is important to notice that in such
cases (i.e., for = ) no interference eects (destructive or constructive) occur for the
LNC case.
In this limiting case, the ratio R‘‘ is illustrated in gure 1 as a function of the
common relative CP phase ( = ) for dierent values of M=N . The lines of gure 1
were obtained via a full numerical4 evaluation of eq. (2.9), and for the example of K ! e
LNV and LNC decays; here we have set M = 350 MeV, and taken an identical strength
for the active-sterile mixings, jU4j jU5j = 105 ( = e; )5; the sterile neutrino total
decay widths are computed following [4, 11, 20].
Similar analyses were carried for other meson decays and dierent avour content of the
nal lepton states (when kinematically allowed); we have conrmed that in all cases the
corresponding R‘‘ exhibit an analogous behaviour to that of gure 1. In addition, such
behaviour is periodic in the phases (mod ).
One can also see from gure 1 that the \nave" limit, R‘‘ = 1, is indeed recovered for
the case of vanishing values of the relative phase , as expected from eq. (3.4). With the
exception of regimes leading to M=N 1 | for which there is no visible interference
eect and one recovers the expectations of the SM extended by one sterile state (i.e.,
R‘‘ ’ 1) | the lines of gure 1 illustrate both constructive and destructive interference
eects in the LNV amplitude, clearly signalling the presence of at least two additional
sterile states.
The constructive interference eects are typically more important for values of ;
for the curves corresponding to very small M=N 1, the constructive interference is
still present (provided M 6= 0), although not visible due to the resolution of the plot.
4The numerical analysis was done following the full computation of [11], adapted to the case of two
additional sterile states.
5Such a choice is inspired by the study of [11], since it leads to contributions to the LNV (and LNC)
BRs within future experimental sensitivity, some modes being already in conict with curent data.
{ 7 {
JHEP09(2019)017
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
