基于MATLAB的PID_控制器设计.doc

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：0.23M 资料格式：doc 举报版权申诉

第1页 / 共11页

dianfeng88-4350999-基于MATLAB的PID_控制器设计.doc.pdf-第2页.png

第2页 / 共11页

dianfeng88-4350999-基于MATLAB的PID_控制器设计.doc.pdf-第3页.png

第3页 / 共11页

dianfeng88-4350999-基于MATLAB的PID_控制器设计.doc.pdf-第4页.png

第4页 / 共11页

dianfeng88-4350999-基于MATLAB的PID_控制器设计.doc.pdf-第5页.png

第5页 / 共11页

dianfeng88-4350999-基于MATLAB的PID_控制器设计.doc.pdf-第6页.png

第6页 / 共11页

dianfeng88-4350999-基于MATLAB的PID_控制器设计.doc.pdf-第7页.png

第7页 / 共11页

dianfeng88-4350999-基于MATLAB的PID_控制器设计.doc.pdf-第8页.png

第8页 / 共11页

文本预览

Matlab 实验报告电气与控制工程学院测控 0802 班任雅月 0806070204 2011．01．08

基于 MATLAB 的 PID 控制器设计 PID 控制是最早发展起来的经典控制策略, 是用于过程控制最有效的策略之一。由于其原理简单、技术成，在实际应用中较易于整定, 在工业控制中得到了广泛的应用。它最大的优点是不需了解被控对象精确的数学模型,只需在线根据系统误差及误差的变化率等简单参数, 经过经验进行调节器参数在线整定, 即可取得满意的结果, 具有很大的适应性和灵活性。 1. PID 控制简介 PID 控制中的积分作用可以减少稳态误差, 但另一方面也容易导致积分饱和, 使系统的超调量增大。微分作用可提高系统的响应速度, 但其对高频干扰特别敏感, 甚至会导致系统失稳。所以, 正确计算控制器的参数, 有效合理地实现 PID 控制器的设计,对于 PID 控制器在过程控制中的广泛应用具有重要的理论和现实意义。在 PID 控制系统中, PID 控制器分别对误差信号 e（t）进行比例、积分与微分运算, 其结果的加权和构成系统的控制信号 u（t），送给对象模型加以控制。 PID 控制器的数学描述为其传递函数可表示为: 从根本上讲, 设计 PID 控制器也就是确定其比例系数 Kp、积分系数 T i 和微分系数 T d , 这三个系数取值的不同, 决定了比例、积分和微分作用的强弱。控制系统的整定就是在控制系统的结构已经确定、控制仪表和控制对象等处在正常状态的情况下, 适当选择控制器的参数使控制仪表的特性和控制对象的特性相配合, 从而使控制系统的运行达到最佳状态, 取得最好的控制效果。下面介绍基于 MATLAB 的 Ziegler-Nichols 算法 PID 控制器设计。 2. PID 控制器的 Ziegler-Nichols 参数整定在实际的过程控制系统中, 有大量的对象模型可以近似地由一阶模型来表示。这个对象模型可以表示为 G(s)  K sT1  sL-e 如果不能建立起系统的物理模型, 可通过试验测取对象模型的阶跃响应, 从而得到模型参数。当然, 我们也可在已知对象模型的情况下, 利用 MATLAB，通过使用 step ( ) 函数得到对象模型的开环阶跃响应曲线。在被控对象的阶跃响应中, 可获取 K 、L 和 T 参数, 也可在 MATLAB 中由 dcgain ( ) 函数求取 K 值。 2

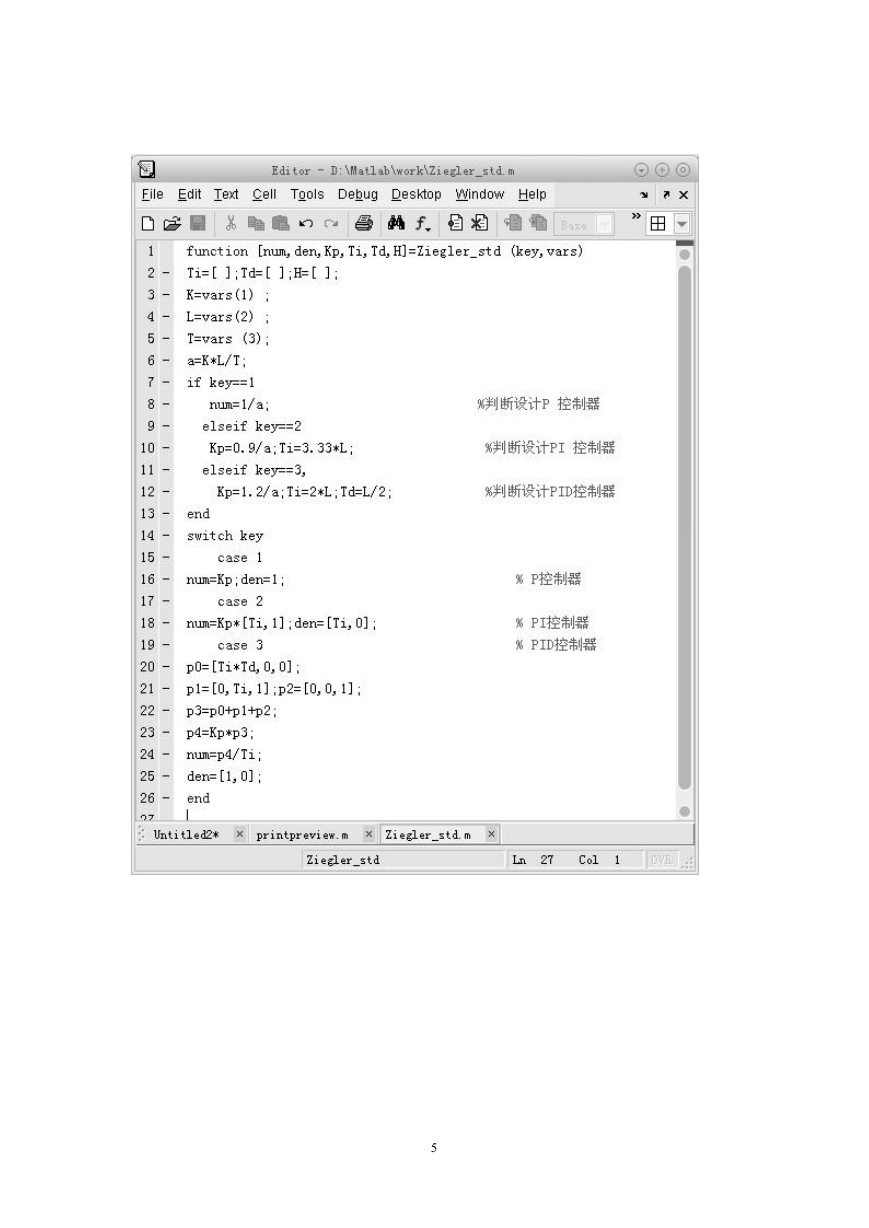
3. 在 MATLAB 下实现 PID 控制器的设计与仿真已知被控对象的 K、L 和 T 值后, 我们可以根据 Ziegler — Nichols 整定公式编写一个 MATLAB 函数 ziegler_std ( )用以设计 PID 控制器。该函数程序如下： function [num,den,Kp,Ti,Td,H]=Ziegler_std (key,vars) Ti=[ ];Td=[ ];H=[ ]; K=vars(1) ; L=vars(2) ; T=vars (3); a=K*L/T; if key==1 num=1/a; elseif key==2 Kp=0.9/a;Ti=3.33*L; elseif key==3, Kp=1.2/a;Ti=2*L;Td=L/2; end switch key case 1 num=Kp;den=1; case 2 case 3 num=Kp*[Ti,1];den=[Ti,0]; p0=[Ti*Td,0,0]; p1=[0,Ti,1];p2=[0,0,1]; p3=p0+p1+p2; %判断设计 P 控制器 %判断设计 PI 控制器 %判断设计 PID 控制器 % P 控制器 % PI 控制器 % PID 控制器 3

p4=Kp*p3; num=p4/Ti; den=[1,0]; end 二、现在选取一个待校正的开环传递函数； G(s)  40.5 2 s （  s(  )4.8 2 2.5 ）利用 PID 控制器的设计来校正将函数 Zidgler_std 输入以下文件并保存。 >> num=[40.5];den=conv(conv([1,2.5],[1,2.5]),conv([1,4.8],[1,4.8])); step(num,den);K=dcgain(num,den) K = >> 0.2813 4

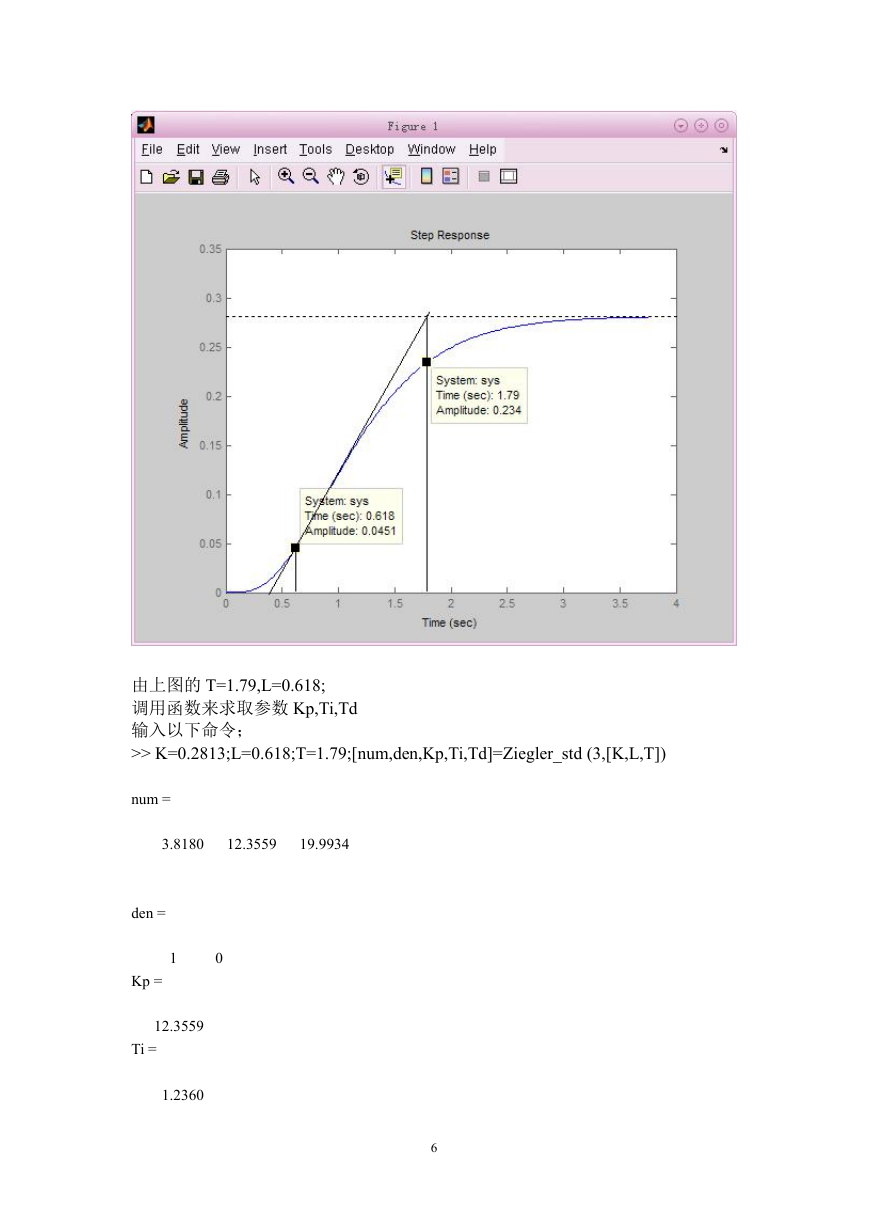
由上图的 T=1.79,L=0.618; 调用函数来求取参数 Kp,Ti,Td 输入以下命令； >> K=0.2813;L=0.618;T=1.79;[num,den,Kp,Ti,Td]=Ziegler_std (3,[K,L,T]) num = 3.8180 12.3559 19.9934 den = Kp = 1 0 12.3559 Ti = 1.2360 6

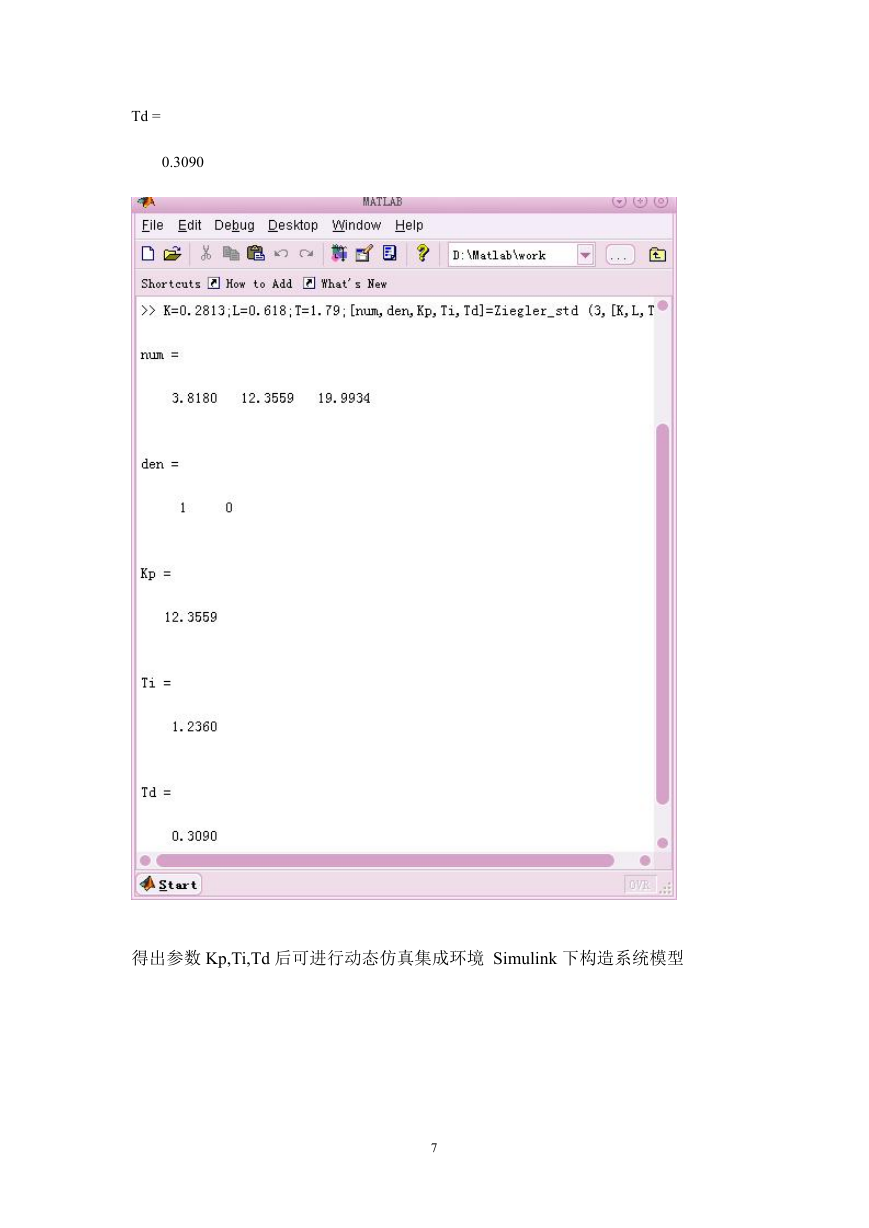
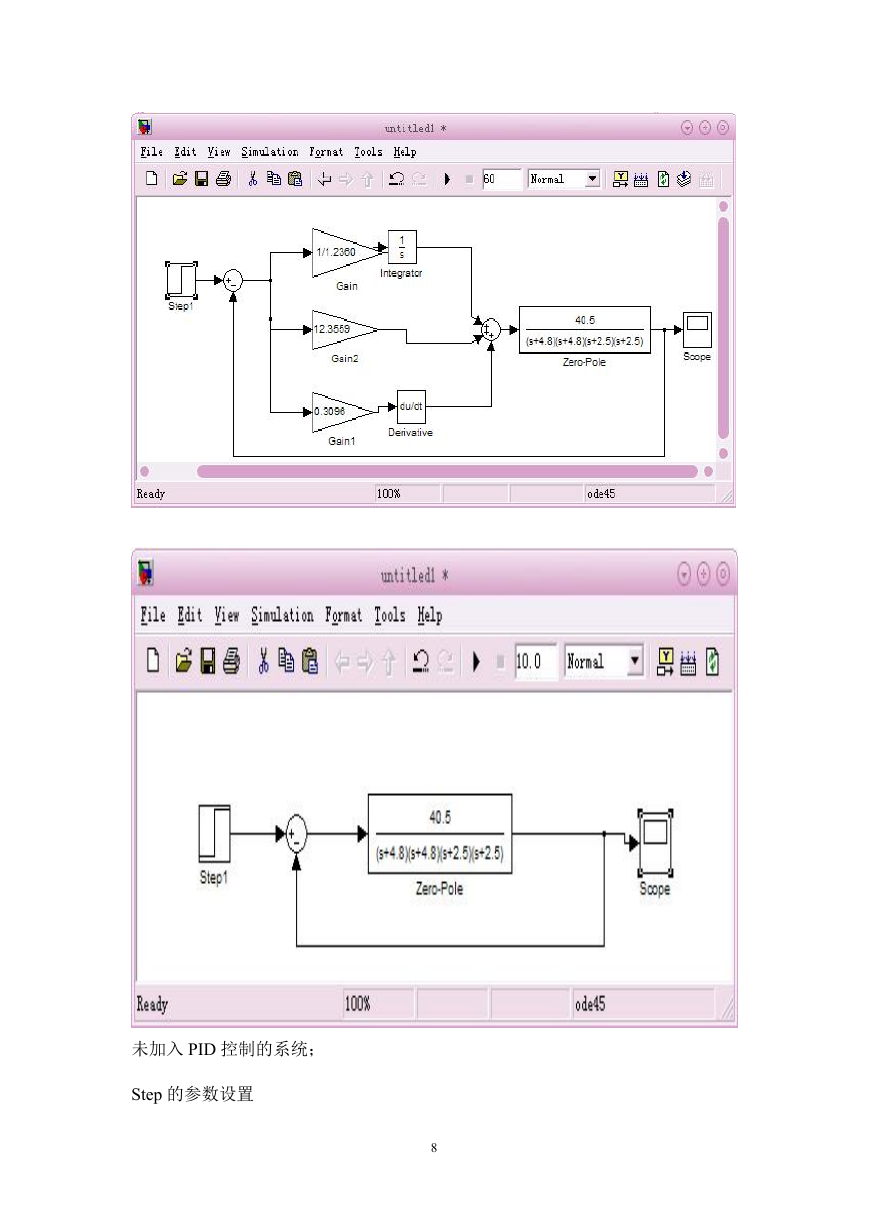
Td = 0.3090 得出参数 Kp,Ti,Td 后可进行动态仿真集成环境 Simulink 下构造系统模型 7

未加入 PID 控制的系统； Step 的参数设置 8

分享到：

赞收藏

资料库

基于MATLAB的PID_控制器设计.doc

相关推荐

课程资源

热门标签

最新资料